AP State Syllabus AP Board 9th Class Maths Solutions Chapter 8 Quadrilaterals InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 8th Lesson Quadrilaterals InText Questions
![]()
Try This
Question
Extend AB to E. Find ∠CBE. What do you notice? What kind of angles are ∠ABC and ∠CBE?
Solution:
Given that □ABCD is a parallelogram and∠A = 40°
∴ ∠ABC = 180°-40° = 140°
∠CBE = 40° ( ∵ ∠A and, ∠CBE are corresponding angles) And ∠CBE and ∠ABC are linear pair of angles.
Do This
Question
Cut out a parallelogram from a sheet of paper again and cut along one of its diagonal. What kind of shapes you obtain ? What can you say about these triangles 7 [Page No. 179]
Solution:
We get two triangles.
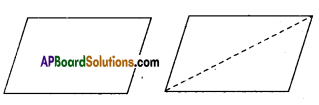
The two triangles are congruent to each other.
Think, Discuss and Write
Question 1.
Show that the diagonals of a square are equal and right bisectors of each other. (Page No. 185)
Solution:
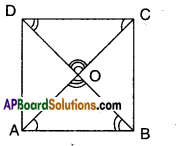
Let □ABCD be a square.
Thus AB = BC = CD = DA
In ΔABC and ΔBAD
AB = AB (common base)
∠B =∠A (each 90°)
BC = AD (equal sides)
∴ ΔABC = ΔBAD (SAS congruence)
⇒ AC = BD (CPCT)
Also in ΔAOB and ΔCOD
∠OAB = ∠OCD [∵ alt. int. angles]
∠OBA = ∠ODC [∵ alt. int. angles]
AB = DC (sides of a square)
∴ ΔAOB = ΔCOD (ASA congruence)
Thus AO = OC (CPCT) ⇒ O is midpoint of AC
Also BO = OD (CPCT) ⇒ O is midpoint of BD
∴ O is midpoint of both AC and BD.
∴ Diagonals bisect each other.
In ΔAOB and ΔCOB
AB = BC (given)
OB = OB (common)
AO = OC (proved)
∴ ΔAOB ≅ ΔCOB (SSS congruence)
∠AOB = ∠COB (CPCT)
But ∠AOB + ∠COB = 180° (∵ linear pair of angles)
∴ ∠AOB = ∠COB = 180°/2 = 90°
Also ∠AOB = ∠COD (∵ vertically opposite angles)
∠BOC = ∠AOD (∵ vertically opposite angles)
∴ AC ⊥ BD
(i.e.,) In a square diagonals bisect at right angles.
Question 2.
Show that the diagonals of a rhombus divide it into four congruent triangles. (Page No. 185)
Solution:
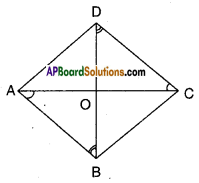
□ABCD is a rhombus
Let AC and BD meet at ‘O’
In ΔAOB and ΔCOD
∠OAB = ∠ODC (alt.int.angles)
AB = CD (def. of rhombus)
∠OBA = ∠ODC (alt. mt, angles)
∴ ΔAOB ≅ΔCOD …………(1)
(ASA congruence)
Thus AO = OC (CPCT
Also ΔAOD ≅ ΔCOD …………..(2)
[ ∵AO = OC; AD = CD; OD = OD SSS congruence]
Similarly we can prove
ΔAOD ≅ ΔCOB …………..(3)
From (1), (2) and (3) we have
ΔAOB = ΔBOC = ΔCOD = ΔAOD
∴ Diagonals of a rhombus divide it into four congruent triangles.
Try This
Question
Draw a triangle ABC and mark the mid points E and F of
two sides of triangle. \(\overline{\mathbf{A B}}\) and \(\overline{\mathbf{A C}}\) respectively. Join the point E and F as shown in the figure. Measure EF and the third side BC of triangle. Also measure ∠AEF and ∠ABC.
We find ∠AEF = ∠ABC and \(\overline{\mathrm{EF}}=\frac{1}{2} \overline{\mathrm{BC}}\)
As these are corresponding angles made by the transversal AB with lines EF and BC, we say EF//BC.
Repeat this activity with some more triangles. (Page No. 188)
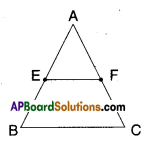
Solution:
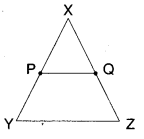
P, Q are mid points of XY and XZ
PQ // YZ
PQ = \(\frac{1}{2}\)YZ
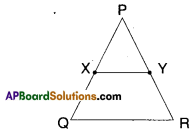
X, Y are mid points of PQ and PR
XY // QR
XY = \(\frac{1}{2}\)QR
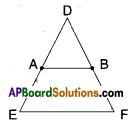
A, B are midpoints of DE and DF
AB // EF
AB = \(\frac{1}{2}\)EF
( ∵ In all cases the pairs of respective corresponding angles are equal.)