AP Inter 1st Year Maths 1A Solutions Chapter 10 త్రిభుజ ధర్మాలు Ex 10(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 10 త్రిభుజ ధర్మాలు Exercise 10(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 10 త్రిభుజ ధర్మాలు Exercise 10(a)

I. ఈ అభ్యాసములోని అన్ని సమస్యలు ΔABC కి సంబంధించినవి.

Question 1.
Σa(sin B – sin C) = 0 అని చూపండి.
Solution:

Question 2.
a = √3 + 1 సెం.మీ., ∠B = 30°, ∠C = 45°, అయితే C ని కనుక్కోండి.
Solution:
∠B = 30°, ∠C = 45°, a = (√3 + 1) సెం.మీ.
A = 180° – (B + C)
= 180° – (30° + 45°)
= 180° – 75°
= 105°

Question 3.
a = 2 సెం.మీ., b = 3 సెం.మీ., c = 4 సెం.మీ., అయితే cos A ని కనుక్కోండి.
Solution:
a = 2 సెం.మీ., b = 3 సెం.మీ., c = 4 సెం.మీ.

Question 4.
a = 26 సెం.మీ., b = 30 సెం.మీ., cos C = \(\frac{63}{65}\) అయితే, c ని కనుక్కోండి. [Mar. ’11]
Solution:
a = 260 సెం.మీ., b = 30 సెం.మీ., cos C = \(\frac{63}{65}\)
∵ c² = a² + b² – 2ab cos C
⇒ c² = 676 + 900 – 2 × 26 × 30 × \(\frac{63}{65}\)
⇒ c² = 1576 – 151
⇒ c² = 64
⇒ c = 8 సెం.మీ.

Question 5.
కోణాలు 1 : 5 : 6 నిష్పత్తిలో ఉంటే, దాని భుజాల నిష్పత్తిని కనుక్కోండి. [May ’07]
Solution:
\(\frac{A}{1}=\frac{B}{5}=\frac{C}{6}\)
B = 5A, C = 6A
A + B + C = 180°
⇒ A + 5A + 6A = 180°
⇒ 12A = 180°
⇒ A = 15°
B = 5A = 75°
C = 6A = 90°
a : b : c = sin A : sin B : sin C
= sin 15° : sin 75° : sin 90°
= \(\frac{\sqrt{3}-1}{2 \sqrt{2}}: \frac{\sqrt{3}+1}{2 \sqrt{2}}: 1\)
= (√3 – 1) : (√3 + 1) : 2√2

Question 6.
2(bc cos A + ca cos B + ab cos C) = a² + b² + c² అని చూపండి. [Mar. ’05]
Solution:
L.H.S. = Σ2bc cos A
= Σ2bc \(\frac{\left(b^2+c^2-a^2\right)}{2 b c}\)
= Σ(b² + c² – a²)
= b² + c² – a² + c² + a² – b² + a² + b² – c²
= a² + b² + c²
= R.H.S.

Question 7.
\(\frac{a^2+b^2-c^2}{c^2+a^2-b^2}=\frac{\tan B}{\tan C}\) అని నిరూపించండి.
Solution:

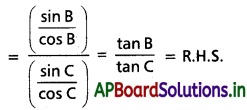
Question 8.
(b + c) cos A + (c + a) cos B + (a + b) cos C = a + b + c అని నిరూపించండి.
Solution:
L.H.S. = (b + c) cos A + (c + a) cos B + (a + b) cos C
= (b cos A + c cos A) + (c cos B + a cos B) + (a cos C + b cos C)
= (b cos C + c cos B) + (a cos C+ c cos A) + (a cos B + b cos A)
= a + b + c
= R.H.S.

Question 9.
(b – a cos C) sin A = a cos A sin C అని నిరూపించండి. [Mar. ’06]
Solution:
(b – a cos C) sin A
= (a cos C + c cos A – a cos C) sin A
= c cos A sin A [∵ b = a cos C + c cos A]
= (2R sin C) cos A sin A
= a cos A sin C (∵ 2R sin A = a)

Question 10.
ఒక త్రిభుజం భుజాలు 4, 5 అవుతూ ఆ భుజాల మధ్య కోణం 60° అయితే, దాని వైశాల్యాన్ని కనుక్కోండి.
Solution:
a = 4, b = 5 వాటి మధ్య కోణం C = 60 ° అనుకుందాం.
ΔABC వైశాల్యం = \(\frac{1}{2}\) × 4 × 5 × sin 60°
= 2 × 5 × sin 60°
= 2 × 5 × \(\frac{\sqrt{3}}{2}\)
= 5√3 చ. సెం.మీ.

Question 11.
\(b \cos ^2 \frac{C}{2}+c \cos ^2 \frac{B}{2}\) = s అని చూపండి.
Solution:

Question 12.
\(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}\) అయితే, ΔABC సమబాహు త్రిభుజమని చూపండి.
Solution:

Question 13.
\(\sin \left(\frac{B-C}{2}\right)=\frac{b-c}{a} \cos \left(\frac{A}{2}\right)\) అని నిరూపించండి.
Solution:

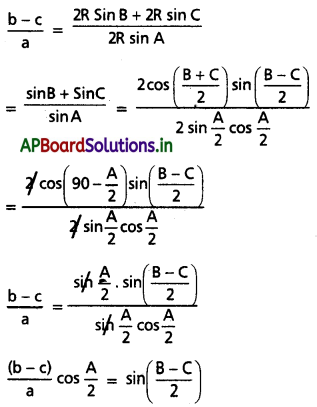
II.

Question 1.
a cos A + b cos B + c cos C = 4R sin A sin B sin C అని నిరూపించండి.
Solution:
L.H.S. = (2R sin A) cos A + (2R sin B) cos B + (2R sin C) cos C
= R (sin 2A + sin 2B + sin 2C)
= R (2 sin(A + B) cos(A – B) + sin 2C)
= R[2 sin(180° – C) cos (A – B) + sin 2C]
= R(2 sin C . cos(A – B) + 2 sin C . cos C)
= 2R sin C (cos(A – B) + cos C)
= 2R sin C (cos(A – B) + cos(180° – \(\overline{A+B}\))
= 2R sin C [cos(A – B) – cos(A + B)]
= 2R sin C (2 sin A sin B)
= 4R sin A sin B sin C
= R.H.S.

Question 2.
Σa³ sin(B – C) = 0 అని నిరూపించండి.
Solution:
L.H.S. = Σ a² [a sin(B – C)]
= Σa² (2R. sin A sin (B-C)]
= RΣa² (2 sin(180° – \(\overline{B+C}\)) sin (B – C))
= RΣa² (2 sin(B + C) . sin(B – C)]
= RΣa² (sin²B – sin²C)
= 2R Σa² \(\left(\frac{b^2}{4 R^2}-\frac{c^2}{4 R^2}\right)\)
= \(\frac{1}{2R}\) Σ[a² (b² – c²)]
= \(\frac{1}{2R}\) [a² (b² – c²) + b² (c² – a²) + c² (a² – b²)]
= \(\frac{1}{2R}\) (a²b² – a²c² + b²c² – a²b²+ a²c² – b²c²)
= \(\frac{1}{2R}\) . 0
= 0
= R.H.S.

Question 3.
\(\frac{a \sin (B-C)}{b^2-c^2}=\frac{b \sin (C-A)}{c^2-a^2}=\frac{c \sin (A-B)}{a^2-b^2}\) అని నిరూపించండి.
Solution:

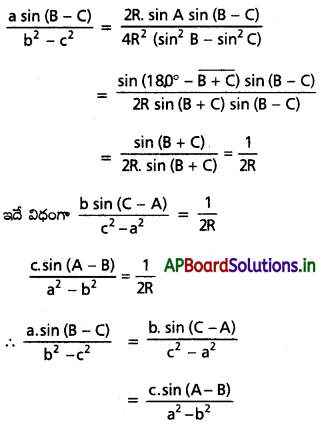
Question 4.
\(\sum \frac{a^2 \sin (B-C)}{\sin B+\sin C}=0\) అని నిరూపించండి.
Solution:

= Σa . 2R(sin B – sin C)
= Σa(2R sin B – 2R sin C)
= Σa(b – c)
= a(b – c) + b(c – a) + c(a – b)
= ab – ac + bc – ab + ca – bc
= 0

Question 5.
\(\frac{a}{b c}+\frac{\cos A}{a}=\frac{b}{c a}+\frac{\cos B}{b}=\frac{c}{a b}+\frac{\cos C}{c}\) అని నిరూపించండి.
Solution:

Question 6.
\(\frac{1+\cos (A-B) \cos C}{1+\cos (A-C) \cos B}=\frac{a^2+b^2}{a^2+c^2}\) అని నిరూపించండి.
Solution:

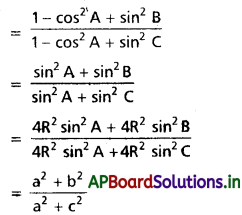
Question 7.
C = 60°, అయితే
(i) \(\frac{a}{b+c}+\frac{b}{c+a}=1\)
(ii) \(\frac{b}{c^2-a^2}+\frac{a}{c^2-b^2}=0\) అని చూపండి.
Solution:
∠C = 60°
⇒ c² = a² + b² – 2ab cos C
⇒ c² = a² + b² – 2ab cos 60°
⇒ c² = a² + b² – 2ab (\(\frac{1}{2}\))
⇒ c² = a² + b² – ab ………(1)

Question 8.
a : b : c = 7 : 8 : 9 అయితే, cos A : cos B : cos C ను కనుక్కోండి. [May ’13]
Solution:

Question 9.
\(\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^2+b^2+c^2}{2 a b c}\) అని చూపండి.
Solution:

Question 10.
(b – a) cos C + c (cos B – cos A) = \(c \sin \frac{A-B}{2} \cdot {cosec} \frac{A+B}{2}\) అని నిరూపించండి.
Solution:
L.H.S. = b cos C – a cos C + c cos B – c cos A
= (b cos C + c cos B) – (a cos C + c cos A)
= a – b
= 2R (sin A – sin B)

Question 11.
\(\text { a. } \sin ^2 \frac{C}{2}+\text { c. } \sin ^2 \frac{A}{2}\) ను s, a, b, c లలో వ్యక్తపరచండి.
Solution:

Question 12.
b + c = 3a అయితే, \(\cot \frac{B}{2} \cdot \cot \frac{C}{2}\) విలువను కనుక్కోండి.
Solution:

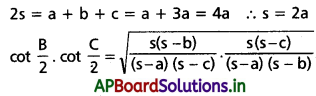
Question 13.
\((b+c) \cos \frac{B+C}{2}=a \cos \frac{B-C}{2}\) అని నిరూపించండి.
Solution:

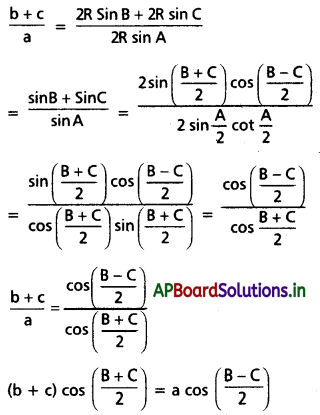
Question 14.
∆ABC లో \(\frac{b^2-c^2}{a^2}=\sin \frac{(B-C)}{(B+C)}\) అని చూపండి. [(A.P) Mar. ’15]
Solution:

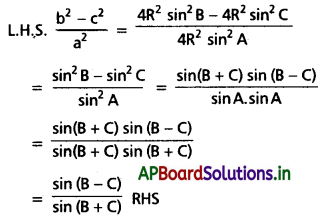
III.

Question 1.
(i) \(\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\frac{s^2}{\Delta}\)
(ii) \(\tan \frac{A}{2}+\tan \frac{B}{2}+\tan \frac{C}{2}\) = \(\frac{b c+c a+a b-s^2}{\Delta}\)
(iii) \(\frac{\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}}{\cot A+\cot B+\cot C}\) = \(\frac{(a+b+c)^2}{a^2+b^2+c^2}\) అని నిరూపించండి.
Solution:

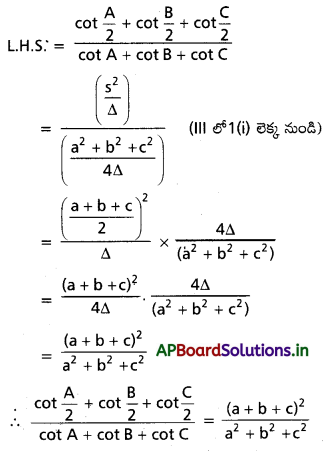
Question 2.
(i) \(\Sigma(a+b) \tan \left(\frac{A-B}{2}\right)=0\)
(ii) \(\frac{\mathbf{b}-c}{\mathbf{b}+c} \cot \frac{A}{2}+\frac{b+c}{b-c} \tan \frac{A}{2}\) = 2 cosec(B – C) అని చూపండి.
Solution:

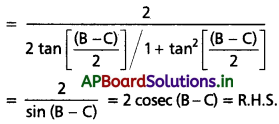
Question 3.
(i) sin θ = \(\frac{\mathbf{a}}{\mathbf{b}+\mathbf{c}}\) అయితే, cos θ = \(\frac{2 \sqrt{b c}}{b+c} \cos \frac{A}{2}\) అని చూపండి. [Mar. ’12]
Solution:

(ii) a = (b + c) cos θ అయితే, sin θ = \(\frac{2 \sqrt{b c}}{b+c} \cos \frac{A}{2}\) అని నిరూపించండి. [May ’11]
Solution:

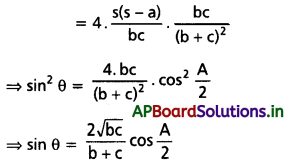
(iii) ఏదైనా కోణం ‘θ’ కు a cos θ = b cos(C + θ) + c cos(B – θ) అని చూపండి.
Solution:
b cos(C + θ) + c cos(B – θ)
= b (cos C . cos θ – sin C sin θ) + c (cos B cos θ + sin B sin θ)
= (b cos C + c cos B) cos θ + (-b sin C + C sin B) sin θ
= a cos θ + (-2R sin B sin C + 2R sin B sin C) sin θ
= a cos θ

Question 4.
ΔABC లోని కోణాలు A.P. లో ఉంటూ b : c = √3 : √2 అయితే, A = 75° అని చూపండి.
Solution:
∵ త్రిభుజ కోణాలు A, B, C లు A.P. లో ఉన్నవి కనుక
⇒ 2B = A + C
⇒ 3B = A + B + C
⇒ 3B = A + B + C
⇒ 3B = 180°
⇒ B = 60°

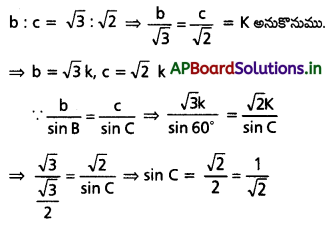
⇒ C = 45°
∴ A = 180° – 60° – 45° = 75°

Question 5.
\(\frac{a^2+b^2}{a^2-b^2}=\frac{\sin C}{\sin (A-B)}\) అయితే, ΔABC సమద్విబాహు లేదా లంబకోణ త్రిభుజమని నిరూపించండి.
Solution:


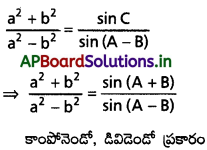
⇒ sin 2A = sin 2B
⇒ A = B
⇒ ΔABC సమద్విబాహు లేదా
2A = 180° – 2B
⇒ A = 90° – B
⇒ A + B = 90°
∴ ΔABC లంబకోణ త్రిభుజం. [∵ A ≠ B]
∴ ABC సమద్విబాహు లేదా లంబకోణ త్రిభుజం.

Question 6.
cos A + cos B + cos C = \(\frac{3}{2}\) అయితే, ΔABC సమబాహు త్రిభుజమని చూపండి.
Solution:

Question 7.
cos²A + cos²B + cos²C = 1 అయితే, ΔABC లంబకోణ త్రిభుజమని నిరూపించండి.
Solution:
cos²A + cos²B + cos²C = 1 …….(1)
ఇప్పుడు cos²A + cos²B + cos²C
= cos²A + 1 – sin²B + cos²C
= 1 + (cos²A – sin²B) + cos²C
= 1 + cos (A + B) cos (A – B) + cos²C
= 1 + cos (180° – C) cos (A – B) + cos²C
= 1 – cos C . cos (A – B) + cos²C
= 1 – cos C (cos (A – B) – cos C)
= 1 – cos C (cos (A – B) – cos (180° – \(\overline{A+B}\)))
= 1 – cos C (cos (A – B) + cos (A + B))
= 1 – cos C (2 cos A cos B)
= 1 – 2 cos A cos B cos C
(1) నుండి, 1 – 2 cos A cos B cos C = 1
⇒ 2 cos A cos B cos C = 0
⇒ cos A = 0 లేదా cos B = 0 లేదా cos C = 0
⇒ A = 90° లేదా B = 90° లేదా C = 90°
∴ ΔABC లంబకోణ త్రిభుజం.

Question 8.
a² + b² + c² = 8R² అయితే, ΔABC లంబకోణ త్రిభుజమని నిరూపించండి.
Solution:
a² + b² + c² = 8R²
⇒ 4R² (sin²A + sin²B + sin²C) = 8R²
⇒ sin²A + sin²B + sin²C = 2 ……..(1)
ఇప్పుడు sin²A + sin²B + sin²C
= 1 – cos²A + sin²B + sin²C
= 1 – (cos²A – sin²B) + sin²C
= 1 – cos (A + B) . cos (A – B) + sin²C
= 1 – cos (180° – C) cos (A – B) + sin²C
= 1 + cos C cos (A – B) + 1 – cos²C
= 2 + cos C (cos (A – B) – cos C)
= 2 + cos C (cos (A – B) – cos (180° – \(\overline{A+B}\)))
= 2 + cos C (cos (A – B) + cos (A + B))
= 2 + cos C (2 cos A cos B)
= 2 + 2 cos A cos B cos C
(1) లో వ్రాయగా
2 + 2 cos A cos B cos C = 2
⇒ 2 cos A cos B cos C = 0
⇒ cos A = 0 లేదా cos B = 0 లేదా cos C = 0
⇒ A = 90° లేదా B = 90° లేదా C = 90°
∴ ΔABC లంబకోణ త్రిభుజము.

Question 9.
\(\cot \frac{A}{2}, \cot \frac{B}{2}, \cot \frac{C}{2}\) లు A.P. లో ఉంటే a, b, c లు A.P. లో ఉంటాయని చూపండి.
Solution:
∵ \(\cot \frac{A}{2}, \cot \frac{B}{2}, \cot \frac{C}{2}\) లు A.P. లో ఉన్నవి.
⇒ \(\frac{(\mathrm{s})(\mathrm{s}-\mathrm{a})}{\Delta}, \frac{(\mathrm{s})(\mathrm{s}-\mathrm{b})}{\Delta}, \frac{(\mathrm{s})(\mathrm{s}-\mathrm{c})}{\Delta}\) లు A.P. లో ఉంటాయి.
⇒ s – a, s – b, s – c లు A.P. లో ఉన్నాయి.
⇒ -a, -b, -c లు A.P. లో ఉంటాయి.
⇒ a, b, c లు A.P. లో ఉంటాయి.

Question 10.
\(\sin ^2 \frac{A}{2}, \sin ^2 \frac{B}{2}, \sin ^2 \frac{C}{2}\) లు H.P. లో ఉంటే a, b, c లు H.P. లో ఉంటాయని చూపండి.
Solution:

Question 11.
C = 90° అయితే \(\left(\frac{a^2+b^2}{a^2-b^2}\right)\) sin (A – B) = 1 అని నిరూపించండి.
Solution:
∵ C = 90° అప్పుడు c² = a² + b²
LHS = \(\frac{a^2+b^2}{a^2-b^2}\) sin (A – B)
= \(\frac{c^2}{a^2-b^2}\) sin (A – B)

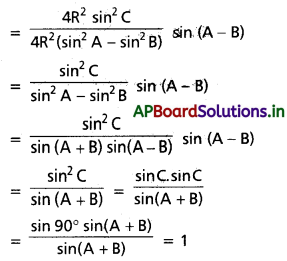
Question 12.
\(\frac{a^2}{4}\) sin 2C + \(\frac{c^2}{4}\) sin 2A = ∆ అని చూపండి.
Solution:
\(\frac{a^2}{4}\) sin 2C + \(\frac{c^2}{4}\) sin 2A
= \(\frac{4 R^2 \sin ^2 A}{4}\) 2 sin C cos C + \(\frac{4 R^2 \sin ^2 C}{4}\) 2 sin A cos A
= 2R² sin²A sin C cos C + 2R² sin²C sin A cos A
= 2R² sin A sin C (sin A cos C + cos A sin C)
= 2R² sin A sin C sin (A + C)
= 2R² sin A sin C sin (180° – B)
= 2R² sin A sin B sin C
= ∆
= RHS

Question 13.
ఒక త్రిభుజాకార స్థలం ABCలో, AC మధ్యబిందువు M వద్ద ఒక దీపస్తంభం ఉంది. BC = 7 మీ., CA = 8 మీ. AB = 9 మీ., ఇంకా B వద్ద దీపస్తంభం చేసే కోణం 15° అయితే దీపస్తంభం ఎత్తు ఎంత?
Solution:

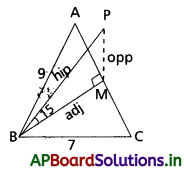
దీప స్తంభము ఎత్తు MP అనుకొండి.
MP = h అనుకొనుము.
∆BMP నుండి tan 15° = \(\frac{h}{BM}\)
(2 – √3) BM = h
ఇచ్చింది AB = 9, BC = 7, AC = 8

Question 14.
ఒక రేవు వద్ద రెండు ఓడలు ఒకే సమయంలో బయలు దేరాయి. ఒకటి గంటకు 24 కి.మీ. వేగంతో N45°E దిశలో, మరొకటి గంటకు 32 కి.మీ. వేగంతో S75°E దిశలో ప్రయాణం చేస్తే, 3 గంటల తరువాత ఓడల మధ్య దూరాన్ని కనుక్కోండి.
Solution:

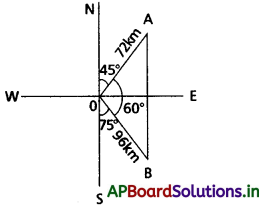
మొదటి ఓడ గంటకు 24 కి. మీ వెళ్తుంది. కనుక 3 గంటల తర్వాత, ఆ ఓడ 72 కి.మీ ప్రయాణం చేస్తుంది.
రెండవ ఓడ గంటకు 32 km వెళ్తుంది. కనుక 3 గంటల తర్వాత, ఆ ఒడ 96 km ప్రయాణం చేస్తుంది.
AB = x అనుకొండి.
∠AOB = 180° – (75° + 45°) = 60°
cosine rule for ∆AOB,
cos 60° = \(\frac{(72)^2+(96)^2-x^2}{2(72)(96)}\)
⇒ \(\frac{1}{2}=\frac{5184+9216-x^2}{13824}\)
⇒ 13824 = 28800 – 2x²
⇒ 2x² = 14976
⇒ x² = 7488
⇒ x = 86.4 (Appx)
∴ 3 గంటల తర్వాత రెండు ఓడల మధ్య దూరం 86.4 km.

Question 15.
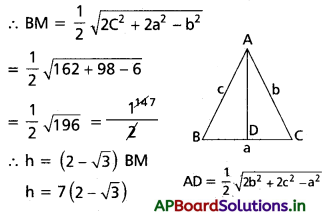
కొండవాలుపై నిటారుగా ఒక చెట్టు ఉన్నది. చెట్టు పాదం నుంచి 35 మీ. దూరంలో A అనే బిందువు నుంచి చెట్టు పై భాగానికి ఊర్థ్వ కోణం 60°. చెట్టు పాదానికి A నుంచి చేసే ఊర్ధ్వ కోణం 15° అయితే చెట్టు ఎత్తు ఎంత?
Solution:
చెట్టు ఎత్తు BC అనుకొండి.
BC = h
BD = x, AD = y అనుకొండి.
AB = 35 m
∆ADB నుంచి, sin 15° = \(\frac{x}{35}\)
\(35\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)\) = x

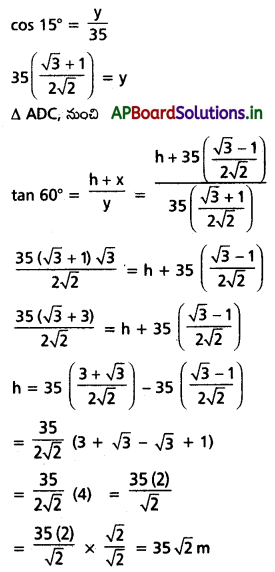
Question 16.
ఒక స్తంభం పాదం నుంచి క్షితిజంపై 40 మీ. దూరంలో ఉన్న బిందువుతో స్తంభం యొక్క \(\frac{3}{4}\)వ పై భాగం \(\tan ^{-1} \frac{3}{5}\) కోణం చేస్తుంది. క్షితిజం నుండి 100 మీ కంటే తక్కువైన ఎత్తుతో స్తంభం ఉంటే స్తంభం ఎత్తు కనుక్కోండి.
Solution:


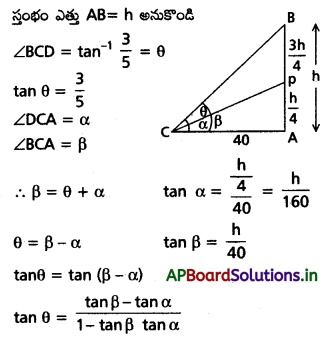
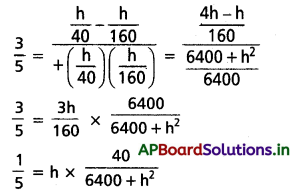
6400 + h² = 200h
h² – 200h + 6400 = 0
h² – 160h – 40h + 6400 = 0
h(h – 160) – 40(h – 160) = 0
(h – 160) (h – 40) = 0
h = 40 or 160
∴ స్తంభం ఎత్తు 100 మీ కంటే తక్కువ కనుక h = 40 m

Question 17.
ఊర్ధ్వంగా ఉండే ఒక స్తంభం AB పాదం B భూమట్టంపైనా, శీర్షం వద్దనూ ఉన్నాయి. ఒక వ్యక్తి భూమి మీద C అనే బిందువు నుండి A ఊర్ధ్వ కోసం 60° గా గమనించాడు. BC రేఖ మీదుగా స్తంభానికి దూరంగా CD = 7మీటర్లు గాగల లి అనే బిందువు వద్దకు వెళ్ళి అక్కడ నుంచి A ఊర్ధ్వ కోణం 45° ఉన్నట్లుగా గమనించాడు. ఆ స్తంభం ఎత్తు ఎంత?
Solution:
స్తంభం ఎత్తు ‘h’ అనుకొండి.
AB = h
CD = 7
∠ACB = 60°, ∠ADB = 45°, Let BC = x

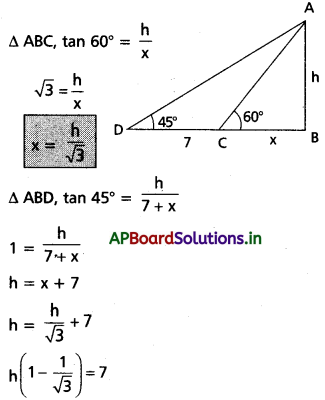
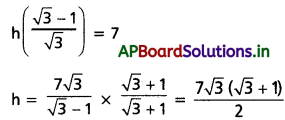
Question 18.
క్షితిజ తలం నుండి h సెం.మీ. ఎత్తులో ఒక లక్ష్యం ఉంది. క్షితిజంతో 15° కోణం చేసే ఒక రేఖపై 10 సెం.మీ. దూరంలో గల P, Q అనే బిందువుల నుండి ఆ లక్ష్యం ఊర్ధ్వ కోణాలు వరసగా 30°, 60° కోణాలు చేస్తే h కనుక్కోండి.
Solution:

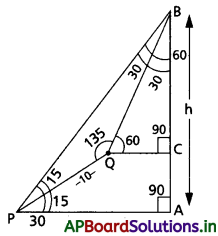
A నుంచి లక్ష్యం B యొక్క ఎత్తు = h మీ.
P & Q లు రెండు లక్ష్యాలు
PQ = 10 సెం.మీ.
∆APB నుండి
∠P = 30°; ∠A = 90°; ∠B = ?
A + P + B = 180°
⇒ 90° + 30° + B = 180°
⇒ B = 180° – 120°
⇒ B = 60°
∆BQC నుండి
∠Q = 60°; ∠C = 90°; ∠B = ?
Q + C + B = 180°
⇒ 60° + 90° + B = 180°
⇒ B = 180° – 150°
⇒ B = 30°
∆BQP నుండి
∠P = 15°; ∠B = 30°; ∠Q = ?
P + B + Q = 180°
⇒ 15° + 30° + Q = 180°
⇒ Q = 180° – 45°
⇒ Q = 135°
Sine rule ఉపయోగించగా


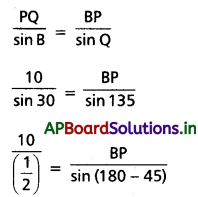
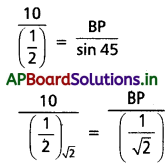
√2 . 10 = BP
∆PAB నుండి
⇒ sin 30° = \(\frac{\mathrm{BA}}{\mathrm{BP}}\)
⇒ BP . sin 30° = AB = h
⇒ √2 . 105 . \(\frac{1}{2}\) = AB = h
⇒ 5√2 = AB = h
⇒ h = 5√2 సెం.మీ.