AP Inter 2nd Year Maths 2B Important Questions Chapter 2 వృత్త సరణులు

Students get through AP Inter 2nd Year Maths 2B Important Questions Chapter 2 వృత్త సరణులు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2B Important Questions Chapter 2 వృత్త సరణులు

ప్రశ్న 1.
x²+y²+4 x-14 y+28=0, x²+y²+4 x-5=0 వృత్తాల మధ్య కోణాన్ని కనుక్కోండి.
సాధన:
దత్త వృత్తాల సమీకరణాలు
x² + y² + 4x- 14y + 28 = 0
x² + y² + 4x – 5 = 0

ప్రశ్న 2.
x²+y² – 12x-6y+41 =0
x²+y²+kx+6y-59=0
ల మధ్య కోణం 45° అయితే k విలువ కనుక్కోండి
సాధన:
x²+y² – 12x-6y+41 =0 ………………….(1)
మరియు x²+y²+kx+6y-59=0 ………………….(2)
వృత్తాల మధ్య కోణము అనుకుందాం

ప్రశ్న 3.
x²+y²-8x – 2y+16=0 ………….. (1)
x²+y²-4x – 4y-1=0 ……………… (2)
వృత్తాలను లంబ చేదనం చేస్తూ, (1,1) గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
కావలసిన వృత్త సమీకరణము
x²+y²+2gx+2fy+c=0 అనుకుందాం ……………… (3)
(3) వృత్తం (1), (2) వృత్తాలకు లంబంగా వుంది.
∴ లంబంగా ఖండించుకొనే నియమాన్ని ఉపయోగిస్తే
2g(-4)+2 f(-1)=c+16 ……………… (4)
2 g(-2)+2 f(-2)=c-1 ……………… (5)
వృత్తం (3), (1,1) ల గుండా పోతుంది
∴ 1²+1²+2 g(1)+2 f(1)+c & =0
2 g+2 f+c+2 =0 ……………… (6)
(4), (5) మరియు (6) లను సాధించగా
\(g=-\frac{7}{3}, f=\frac{23}{6}, c=-5\)
కావలసిన వృత్త సమీకరణము
3(x²+y²)-14 x+23 y-15=0

ప్రశ్న 4.
x²+y²+2x+17y+4=0 ………….. (1)
x²+y²+7x+6y+11=0 ………….. (2)
x²+y²-x+22y+3=0 …………..  (3)
లకు లంబంగా ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి.
Answer:
కావలసిన వృత్త సమీకరణం
x²+y²+2gx+2fy+c=0 అనుకుందాం ………….. (4)
(1), (2) మరియు (3) లు ఈ వృత్తాలు లంబంగా ఖండిస్తాయి.
2(g)(1)+2(f)\(\left(\frac{7}{2}\right)\) = c+4 ………….. (5)
2(g)\(\left(\frac{7}{2}\right)\)+2(f)(3)=c+11 ………….. (6)
2(g)\(\left(-\frac{1}{2}\right)\)+2(f)(11)=c+3 ………….. (7)
(5), (6) మరియు (7) లను సాధించగా g = – 3, f=-2 మరియ c =-44
కావలసిన వృత్త సమీకరణము
x²+y²-6 x – 4y – 44=0

ప్రశ్న 5.
x cos α + y sin α= p ……………. (1) సమీకరణం సూచించే రీఖ x²+y²=a² ……………. (2) వృత్తాన్ని A, B బిందువుల వద్ద ఖండిస్తే \(\overline{\mathbf{A B}}\) వ్యాసంగా ఉండే వృత్త సమీకరణం (x²+y²-a²)-2p(x cos α +y sin α -p )=0 అని చూపండి.
సాధన:
A, B ల గుండా పోయే వృత్త సమీకరణం
(x²+y²-a² right)+λ (x cosα +y sin α -p)=0 …………………….. (3)
వృత్త కేంద్రము \(\left(-\frac{\lambda \cos \alpha}{2},-\frac{\lambda \sin \alpha}{2}\right)\)
సమీకరణం (3) సూచించే వృత్తానికి \(\overline{A B}\) వ్యాసం కావాలంటే దీని కేంద్రం (1) పై ఉండాలి.
∴ \(-\frac{\lambda \cos \alpha}{2}(\cos \alpha)-\frac{\lambda \sin \alpha}{2}(\sin \alpha)=p\)
అంటే \(-\frac{\lambda}{2}\)(cos ²α+sin² α)=p
అంటే λ =-2 p
కావలసిన వృత్త సమీకరణము
(x²+y²-a²)-2 p(x cos α+y sin α -p)=0

ప్రశ్న 6.
X² + y²– 8x – 6y + 21 = 0 …………….. (1)
x²+y² – 2x-15= 0 …………….. (2)
వృత్తాల ఖండన బిందువుల గుండా (1,2) బిందువు గుండా పోమే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
(1), (2) వృత్తాల ఖండన బిందువు గుండా పోమే వృత్తం
(x²+y²-8 x-6 y+21)
λ (x²+y²-2 x-15)=0 …………….. (3)
ఈ వృత్తం (1,2) గుండా పోతుంది.
(1+4-8-12 +21)
+λ(1+4-2-15)=0
అంటే 6+ λ(-12)=0
అంటే λ = \(\frac{1}{2}\)
కావలసిన వృత్త సమీకరణము
(x²+y²-8 x-6 y+21)
+ \(\frac{1}{2}\) (x²+y²-2 x-15)=0
అంటే 3(x²+y²)-18 x-12 y+27=0

ప్రశ్న 7.
కింది వృత్లాలతో ఏర్పడిన మాలకేంద్రాన్ని కనుక్కోండి.
x²+y²-2x+6 y=0 …………….. (1)
x²+y²-4 x-2 y+6=0 ……………. (2)
x²+y²-12 x+2 y+3=0 ……………. (3)
సాధన:
(1), (2), (3) వృత్తాల మూలాక్షాలు
x+4 y-3=0 ……………. (4)
8 x-4 y+3=0 ……………. (5)
10 x+4 y-3=0 ……………. (6) (4), (5) లను సాధిస్తే ఖండన దిందువు \(\left[0, \frac{3}{4}\right]\) ఇది దత్త వృత్త మూలకేంద్రము

ప్రశ్న 8.
S ≡ x²+y²+3 x+5 y+4=0 …………… (1)
S’ ≡ x²+y²+5 x+3 y+4=0 …………… (2)
ల ఉమ్మడి జ్యా సమీంరణం, దాని పొడవును కనుక్రోండి.
సాధన:
దత్త వృత్తాల సమీకరణాలు
S ≡ x²+y²+3 x+5 y+4=0 …………… (1)
మరియు S’ ≡ x²+y²+5 x+3 y+4=0 …………… (2)
ఉమ్మడి జ్యసమీకరణం S-S′=0
-2 x+2 y=0
L ≡ x-y=0

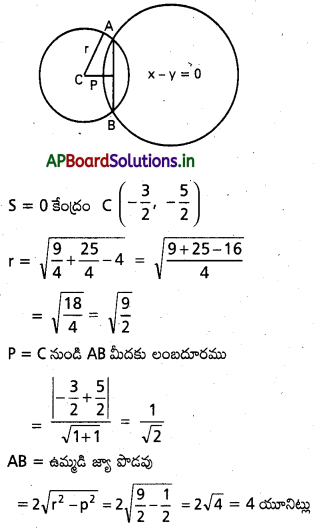
ప్రశ్న 9.
S ≡ x²+y² – 2x – 4y -20 = 0 ……….. (1)
S ≡ x² + y² + 6x + 2y – 90 = 0 ……….. (2)
వృత్తాలు అంతరంగా స్పృశించుకుంటాయని చూపండి. ఇంకా స్ర్శబిందువును, ఈ బిందువు వద్ద ఉమ్మడి, స్పర్శరేఖను కనుక్కోండి.
సాధన:
C₁ C₂ లు కేంద్రాలు మరియు r₁, r₂ లు వ్యాసార్థాలు
C₁=(1,2) ; C₂=(-3,-1) ; r₁=5 ; r₂=10
C₁ C₂=కేంద్రాల మధ్యదూరము = 5
\(\left|r_1-r_2\right|=|5-10|=5=C_1 C_2\)
∴ దత్త వృత్తాలు అంతరంగా స్పృశించుకుంటాయి. ఉమ్మడి జ్యానే మాలక్షము S-S’=0 దాని సమీకరణము.
4 x+3 y-35=0
ఇప్పుడు స్పర్శ ఐిందువును కనుగొందాం
స్పర్య బిందువు C₁ C₂ ను 5: 10 అంటే 1: 2 నిష్పత్తిలో
బాహ్యంగా విభజిస్తుంది.
స్పర్యు బిందువు = \(\left(\frac{(1)(-3)-2(1)}{1-2}, \frac{(1)(-1)-2(2)}{1-2}\right)\)
= (5,5)

ప్రశ్న 10.
S ≡ x²+y²+2x+3y+1=0 ……………….. (1)
S’ ≡ x²+y²+4x+3y+20 ……………… (2)
ల ఉమ్మడి జ్యా వ్యాసంగా గల వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
(1) మరియు (2) ల ఉమ్మడి జ్యానే మూలాక్షం.
సమీకరణం S-S’=0.
అంటే 2x+1=0 ……………… (3)
(1), (3) ల ఖండన బిందువు గుండా ఏదేనా పోమే వృత్తము
(S+λL=0)
(x²+y²+2 x+3 y+1)+λ(2 x+1)=0
x²+y²+2(λ+1) x+3y+ (1+λ)=0 …………………… (4)
వృత్త కేంద్రం  \(\left(-(\lambda+1), \frac{3}{2}\right)\)
సమీకరణం (4) సూచించే వృత్తానికి 2 x+1= 0 ఒక జ్యా. ఈ జ్యా వృత్తం (4) నకు వ్యాసమయితే (4) కేంద్రం (3) మీద ఉంటుంది.
∴ 2{-(λ+1)}+1=0
⇒ λ = – \(\frac{1}{2}\)
(1), (2) ల ఉమ్మడి జ్యా వ్యాసంగా గల వృత్త సమీకరణము
(λ =\(\frac{1}{2}\) ను సమీకరణం (4) లో (ప్రకక్షేపించిన)
2(x²+y²)+2 x+6 y+1=0

ప్రశ్న 11.
(కింది వృత్తాలలోని ప్రతి వృత్తాన్ని లంబ చేదనం చేసే వృత్త సమీకరణాన్ని కనుక్కొందాం.
S’ ≡ x²+y²+3x+2y+1 =0 ………………  (1)
S’’ ≡ x² + y²-x + 6y + 5 = 0 ………………  (2)
S’’’ ≡ x² + y² + 5x – 8y+ 15 = 0 ……………… (3)
సాధన:
కావలసిన వృత్త కేంద్రం దత్త వృత్తాల మాలకేంద్రం. మూలకేంద్రం నుండి ఈ వృత్లాలకు గీయబడిన స్పర్శరేఖ పొడవు కావలసిన వృత్త వ్యాసార్థము
(1), (2) ల మూలాక్షం
x – y = 1 …………….  (4)
(2), (3) ల మూలాక్షము
3 x-7 y=-5 ……………. (5)
(4), (5)ల ఖండన బిందువు (3,2). (1), (2) మరియు (3) వృత్తాల మూలకేంద్రం (3,2)(3,2) నుండి (1) వృత్తానికి స్పర్శరేఖ
పొడవు \(=\sqrt{3^2+2^2+3(3)+2(2)+1}=3 \sqrt{3}\)
కావలసిన వృత్త సమీకరణము
(x-3)²+(y-2)²=\((3 \sqrt{3})^2\)
x²+y²-6 x-4 y-14=0