AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Ex 3(c)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 3 మాత్రికలు Exercise 3(c) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Exercise 3(c)

I.

Question 1.
A = \(\left[\begin{array}{ccc}
2 & 0 & 1 \\
-1 & 1 & 5
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-1 & 1 & 0 \\
0 & 1 & -2
\end{array}\right]\) అయితే (AB’)’ ను కనుక్కోండి.
Solution:

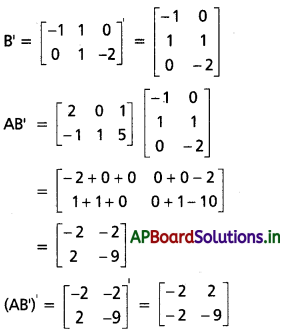
Question 2.
A = \(\left[\begin{array}{cc}
-2 & 1 \\
5 & 0 \\
-1 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-2 & 3 & 1 \\
4 & 0 & 2
\end{array}\right]\) అయితే 2A + B’, 3B’ – A లను కనుక్కోండి.
Solution:

Question 3.
A = \(\left[\begin{array}{cc}
2 & -4 \\
-5 & 3
\end{array}\right]\) అయితే A + A’, A . A’ లను కనుక్కోండి. [May ’07]
Solution:
A = \(\left[\begin{array}{cc}
2 & -4 \\
-5 & 3
\end{array}\right]\)

Question 4.
A = \(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\) ఒక సౌష్ఠవ మాత్రిక అయితే x విలువ ఎంత? [Mar. ’03]
సూచన : ‘A’ ఒక సౌష్ఠవ మాత్రిక ⇒ A^T = A
Solution:
A సౌష్టవ మాత్రిక
⇒ A^T = A
\(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
2 & 5 & x \\
3 & 6 & 7
\end{array}\right]=\left[\begin{array}{ccc}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\)
∴ x = 6

Question 5.
A = \(\left[\begin{array}{ccc}
0 & 2 & 1 \\
-2 & 0 & -2 \\
-1 & x & 0
\end{array}\right]\) ఒక వక్ర సౌష్ఠవ మాత్రిక అయితే x విలువ ఎంత? [May ’13]
సూచన: ‘A’ ఒక వక్ర సౌష్ఠవ మాత్రిక ⇒ A^T = -A
Solution:
A ఒక వక్ర సౌష్టవ మాత్రిక
⇒ A^T = -A

∴ x = 2

Question 6.
\(\left[\begin{array}{ccc}
0 & 1 & 4 \\
-1 & 0 & 7 \\
-4 & -7 & 0
\end{array}\right]\) ఒక సౌష్ఠవ మాత్రిక అవుతుందా, వక్ర సౌష్ఠవ మాత్రిక అవుతుందా?
Solution:

∴ A ఒక వక్ర సౌష్ఠవ మాత్రిక.

II.

Question 1.
A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\) అయితే AA’ = A’A = I అని చూపండి. [Mar. ’07]
Solution:

Question 2.
A = \(\left[\begin{array}{ccc}
1 & 5 & 3 \\
2 & 4 & 0 \\
3 & -1 & -5
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
2 & -1 & 0 \\
0 & -2 & 5 \\
1 & 2 & 0
\end{array}\right]\) అయితే 3A – 4B’ ను కనుక్కోండి.
Solution:

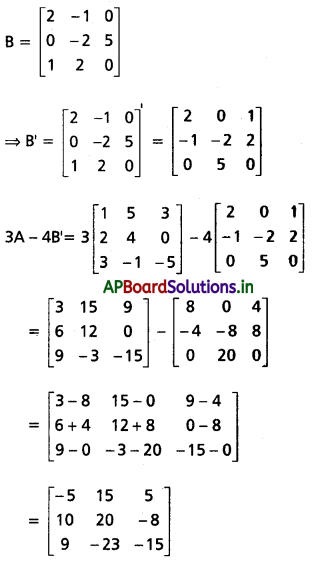
Question 3.
A = \(\left[\begin{array}{cc}
7 & -2 \\
-1 & 2 \\
5 & 3
\end{array}\right]\), B = \(\left[\begin{array}{cc}
-2 & -1 \\
4 & 2 \\
-1 & 0
\end{array}\right]\) అయితే AB’ మరియు BA’ లను కనుక్కోండి.
Solution:

Question 4.
A ఒక చతురస్ర మాత్రిక అయితే AA’ సౌష్ఠవ మాత్రిక అని చూపండి. [(A.P) Mar. ’15]
Solution:
A చతురస్ర మాత్రిక
(AA’)’ = (A’)’ A’ = A . A’
∵ (AA’)’ = AA’
⇒ AA’ ఒక సౌష్ఠవ మాత్రిక.