Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 4 సదిశల సంకలనం Exercise 4(a) will help students to clear their doubts quickly.
AP Inter 1st Year Maths 1A Solutions Chapter 4 సదిశల సంకలనం Exercise 4(a)
I.
Question 1.
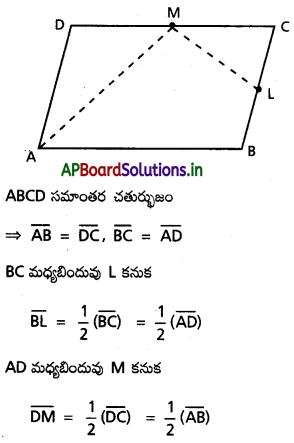
ABCD సమాంతర చతుర్భుజంలో BC, CD ల మధ్య బిందువులు వరుసగా L, M అయితే
(i) \(\overline{\mathrm{AL}}\), \(\overline{\mathrm{AM}}\) లను \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{AD}}\) లలో కనుక్కోండి.
(ii) \(\overline{\mathbf{A M}}=\lambda \overline{\mathrm{AD}}-\overline{\mathrm{LM}}\) అయితే λ విలువ కనుక్కోండి.
Solution:


Question 2.
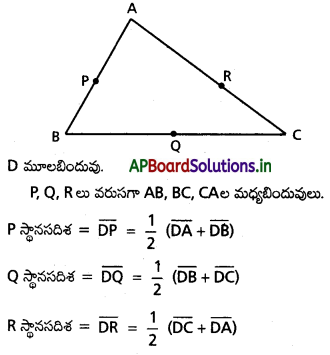
∆ABC లో AB, BC, CA ల మధ్య బిందువులు వరుసగా P, Q, R. ‘D’ ఏదైనా బిందువు అయితే,
(i) \(\overline{\mathrm{DA}}+\overline{\mathrm{DB}}+\overline{\mathrm{DC}}\) ను \(\overline{\mathbf{D P}}, \overline{\mathbf{D Q}}, \overline{\mathbf{D R}}\) లలో వ్యక్తపరచండి.
(ii) \(\overline{\mathrm{PA}}+\overline{\mathrm{QB}}+\overline{\mathrm{RC}}=\bar{\alpha}\) అయితే \(\bar{\alpha}\) ను కనుక్కోండి.
Solution:

![]()
Question 3.
\(\overline{\mathbf{a}}=\overline{\mathbf{i}}+\mathbf{2} \overline{\mathbf{j}}+\mathbf{3} \overline{\mathbf{k}}, \overline{\mathbf{b}}=\mathbf{3} \overline{\mathbf{i}}+\overline{\mathbf{j}}\) అనుకోండి. \(\overline{\mathbf{a}}+\overline{\mathbf{b}}\) దిశలో యూనిట్ సదిశను కనుక్కోండి.
Solution:

Question 4.
సదిశలు \(-\mathbf{3} \overline{\mathbf{i}}+\mathbf{4} \overline{\mathbf{j}}+\lambda \overline{\mathbf{k}}, \mu \overline{\mathbf{i}}+\mathbf{8} \overline{\mathbf{j}}+\mathbf{6} \overline{\mathbf{k}}\) సరేఖీయాలైతే, λ, µ లను కనుక్కోండి. [Mar. ’14; May ’12]
Solution:

Question 5.
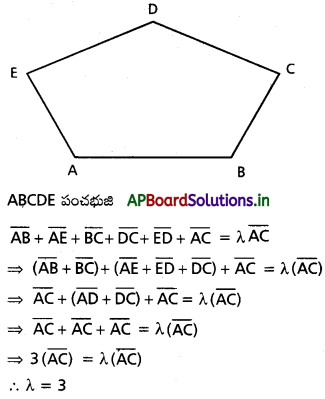
పంచభుజి ABCDE లో \(\overline{\mathbf{A B}}, \overline{\mathbf{A E}}, \overline{\mathbf{B C}}, \overline{\mathbf{D C}}, \overline{\mathbf{E D}}\), \(\overline{\mathbf{A C}}\) ల మొత్తం λ \(\overline{\mathbf{A C}}\) అయితే, λ విలువను కనుక్కోండి.
Solution:
Question 6.
A, B, C బిందువుల స్దాన దిశలు వరుసగా \(-\mathbf{2} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}\), \(-4 \overline{\mathbf{i}}+2 \bar{j}+2 \overline{\mathbf{k}}, 6 \overline{\mathbf{i}}-3 \overline{\mathbf{j}}-13 \overline{\mathbf{k}}\) అవుతూ \(\overline{\mathbf{A B}}=\lambda \overline{\mathrm{AC}}\) అయితే λ విలువను కనుక్కోండి.
Solution:
‘O’ మూలబిందువు.

Question 7.
\(\overline{\mathbf{O A}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{A B}}=\mathbf{3} \overline{\mathbf{i}}-\mathbf{2} \overline{\mathbf{j}}+\overline{\mathbf{k}}\), \(\overline{\mathbf{B C}}=\overline{\mathbf{i}}+\mathbf{2} \overline{\mathbf{j}}-\mathbf{2} \overline{\mathbf{k}}, \overline{\mathbf{C D}}=\mathbf{2} \overline{\mathbf{i}}+\overline{\mathbf{j}}+\mathbf{3} \overline{\mathbf{k}}\), అయితే \(\overline{O D}\) సదిశను కనుక్కోండి. [May ’13]
Solution:

![]()
Question 8.
\(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}+\mathbf{5} \overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{b}}=\mathbf{4} \overline{\mathbf{i}}+\mathbf{m} \overline{\mathbf{j}}+\mathbf{n} \overline{\mathbf{k}}\) లు సరేఖీయ సదిశలైతే m, n లను కనుక్కోండి. [(T.S), Mar ’15; May ’11]
Solution:

Question 9.
\(\overline{\mathbf{a}}=\mathbf{2 i}+\mathbf{4} \overline{\mathbf{j}}-5 \overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{c}}=\overline{\mathbf{j}}+\mathbf{2 \overline { \mathbf { k } }}\) అయితే \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}\) సదిశకు అభిముఖ దిశలో యూనిట్ సదిశను కనుక్కోండి. [(A.P) Mar. ’15 ’12, ’04; May ’12]
Solution:

Question 10.
\(3 \bar{i}+5 \bar{j}+2 \bar{k}, 2 \bar{i}-3 \bar{j}-5 \bar{k},-5 \bar{i}-2 \bar{j}+3 \bar{k}\) సదిశలతో ఏర్పడే త్రిభుజం, సమబాహు త్రిభుజం అవుతుందా?
Solution:
∆ABC భుజాలు
\(\overline{\mathrm{AB}}=3 \overline{\mathrm{i}}+5 \overline{\mathrm{j}}+2 \overline{\mathrm{k}}\)

Question 11.
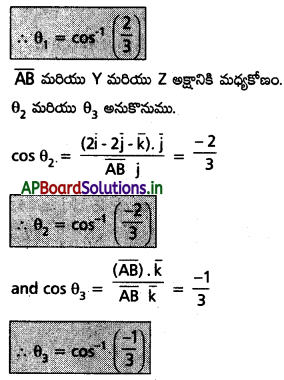
\(3 \bar{i}-6 \bar{j}+2 \bar{k}\) సదిశ నిరూపక అక్షాలతో ధనాత్మక దిశలో α, β, γ కోణాలు చేస్తుంటే cos α, cos β, cos γ లను కనుక్కోండి.
Solution:

![]()
Question 12.
(1, -3, 2), (3, -5, 1) ల గుండా పోయే సరళరేఖ నిరూపకాక్షాలతో చేసే కోణాలను కనుక్కోండి.
Solution:
నిరూపకాక్షాలతో యూనిట్ సదిశలు వరసగా \(\bar{i}, \bar{j}, \bar{k}\).
ఇచ్చిన బిందువు A(1, -3, 2) మరియు B(3, -5, 1) మూల బిందువు ‘O’ అనుకొనుము.

II.
Question 1.
\(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}=\alpha \overline{\mathbf{d}}, \overline{\mathbf{b}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}=\beta \overline{\mathbf{a}}, \overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతలీయ సదిశలైతే \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}=\mathbf{0}\) అని చూపండి.
Solution:


Question 2.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతలీయ సదిశలైతే, ఈ కింది నాలుగు బిందువులు సతలీయాలని చూపండి. [May ’12]
(i) \(-\bar{a}+4 \bar{b}-3 \bar{c}, 3 \bar{a}+2 \bar{b}-5 \bar{c}\), \(-3 \bar{a}+8 \bar{b}-5 \bar{c},-3 \bar{a}+2 \bar{b}+\bar{c}\)
Solution:
‘O’ మూలబిందువు, A, B, C, D లు దత్త బిందువులు.

ఏదేని ఒక సదిశను మిగిలిన రెండు సదిశల రేఖీయ సంయోగంగా వ్రాస్తే,

A, B, C, D లు సతలీయాలు.
∴ దత్త బిందువులు సతలీయాలు.
(ii) \(6 \bar{a}+2 \bar{b}-\bar{c}, 2 \bar{a}-\bar{b}+3 \bar{c},-\bar{a}+2 \bar{b}-4 \bar{c}\), \(-12 \bar{a}-\bar{b}-3 \bar{c}\) [(T.S) Mar. ’15]
Solution:
‘O’ మూలబిందువు. A, B, C, D లు దత్త బిందువులు.


![]()
Question 3.
\(\overline{\mathbf{i}}, \overline{\mathbf{j}}, \overline{\mathbf{k}}\) ధన నిరూపకాక్షాల వెంబడి యూనిట్ సదిశలైతే, \(\mathbf{4} \overline{\mathbf{i}}+5 \overline{\mathbf{j}}+\overline{\mathbf{k}},-\overline{\mathbf{j}}-\overline{\mathbf{k}}, 3 \overline{\mathbf{i}}+9 \overline{\mathbf{j}}+4 \overline{\mathbf{k}}\), \(-4 \bar{i}+4 \bar{j}+4 \bar{k}\) అనే నాలుగు బిందువులు సతలీయాలని చూపండి. [Mar. ’14]
Solution:
‘O’ మూలబిందువు. A, B, C, D లు దత్త బిందువులు.



Question 4.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతలీయ సదిశలైతే ఈ కింద ఇచ్చిన స్థాన సదిశల బిందువుల సరేఖీయత పరీక్షించండి.
(i) \(\bar{a}-2 \bar{b}+3 \bar{c}, 2 \bar{a}+3 \bar{b}-4 \bar{c},-7 \bar{b}+10 \bar{c}\)
Solution:
‘O’ మూలబిందువు, A, B, C లు దత్త బిందువులు.

(ii) \(3 \bar{a}-4 \bar{b}+3 \bar{c},-4 \bar{a}+5 \bar{b}-6 \bar{c}\), \(4 \bar{a}-7 \bar{b}+6 \bar{c}\)
Solution:
‘O’ మూలబిందువు. A, B, C లు దత్తబిందువులు


(iii) \(2 \bar{a}+5 \bar{b}-4 \bar{c}, \bar{a}+4 \bar{b}-3 \bar{c}, 4 \bar{a}+7 \bar{b}-6 \bar{c}\)
Solution:
‘O’ మూలబిందువు. A, B, C లు దత్త బిందువులు.

III.
Question 1.
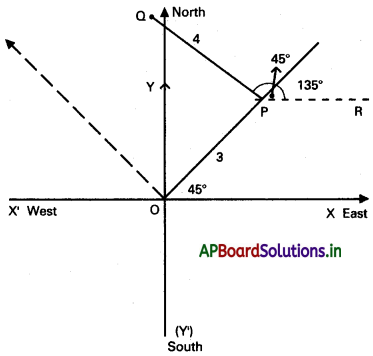
కార్టీసియన్ తలంలో మూలబిందువు O. ఒక వ్యక్తి O నుంచి ఈశాన్య (NORTH-EAST) దిశలో 3 యూనిట్లు నడచి P అనే బిందువును చేరుకున్నాడు. అక్కడనుంచి వాయవ్య (NORTH-WEST) దిశకు సమాంతరంగా 4 యూనిట్లు నడిచి, Q అనే బిందువును చేరుకున్నాడు. OQ సదిశను \(\overline{\mathbf{i}}, \overline{\mathbf{j}}\) లలో కనుక్కోండి. (ఇక్కడ ∠XOP = 45°).
Solution:
‘O’ మూలబిందువు
∠ХОР = 45°

![]()
Question 2.
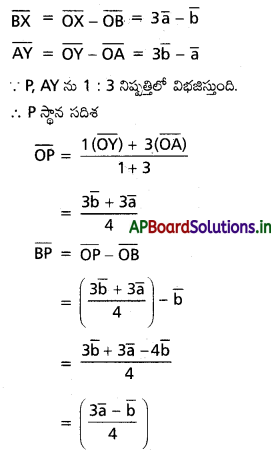
O, A, B, X, Y బిందువులు \(\overline{\mathbf{O A}}=\overline{\mathbf{a}}, \overline{\mathbf{O B}}=\overline{\mathbf{b}}\), \(\overline{\mathbf{O X}}=3 \overline{\mathbf{a}}, \overline{\mathbf{O Y}}=\mathbf{3} \overline{\mathbf{b}}\) అయ్యేటట్లు ఉంటే \(\overline{\mathrm{BX}}\), \(\overline{\mathrm{AY}}\) సదిశలను \(\overline{\mathbf{a}}, \overline{\mathbf{b}}\) లలో రాయండి. ఇంకా P అనే బిందువు AY ను 1 : 3 నిష్పత్తిలో విభజిస్తే \(\overline{\mathbf{B P}}\) ని \(\overline{\mathbf{a}}, \overline{\mathbf{b}}\) లలో రాయండి.
Solution:
\(\overline{O A}=\bar{a}, \overline{O B}=\bar{b}, \overline{O X}=3 \bar{a}, \overline{O Y}=3 \bar{b}\)
Question 3.
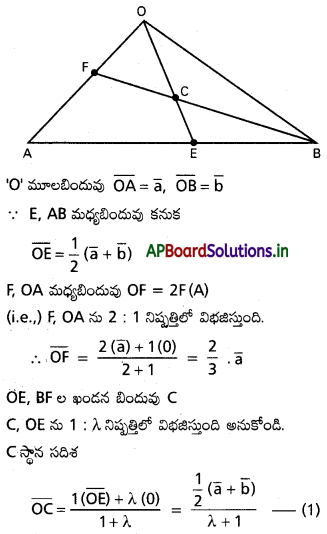
∆OAB లో AB మధ్యబిందువు E, OF = 2FA అయ్యేలా OA మీద F ఒక బిందువు. OE, BF ల ఖండన బిందువు C అయితే OC : CE, BC : CF నిష్పత్తులను కనుక్కోండి.
Solution:


![]()
Question 4.
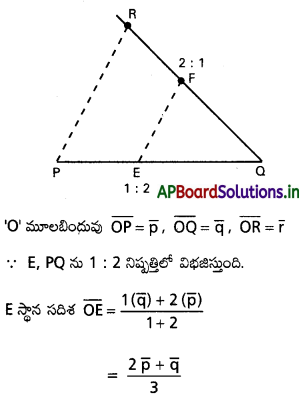
PQ రేఖాఖండాన్ని E బిందువు 1 : 2 నిష్పత్తిలో అంతరంగా విభజిస్తుంది. PQ రేఖపై లేని బిందువు R. QF : FR = 2 : 1 అయ్యేటట్లు QR మీద F ఒక బిందువు అయితే PR కు EF సమాంతరంగా ఉంటుందని చూపండి.
Solution: