AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(d)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(d) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(d)

I.

Question 1.
కింది వాటిని సూక్ష్మీకరించండి.
(i) \(\frac{\sin 2 \theta}{1+\cos 2 \theta}\)
Solution:
\(\frac{\sin 2 \theta}{1+\cos 2 \theta}\)
= \(\frac{2 \sin \theta \cos \theta}{2 \cos ^2 \theta}\)
= tan θ

(ii) \(\frac{3 \cos \theta+\cos 3 \theta}{3 \sin \theta-\sin 3 \theta}\)
Solution:
\(\frac{3 \cos \theta+4 \cos ^3 \theta-3 \cos \theta}{3 \sin \theta-\left(3 \sin \theta-4 \sin ^3 \theta\right)}=\frac{4 \cos ^3 \theta}{4 \sin ^3 \theta}=\cot ^3 \theta\)

Question 2.
కింది వాటిని గణించండి.
(i) 6 sin 20° – 8 sin³20°
Solution:
6 sin 20° – 8 sin³20°
= 2(3 sin 20° – 4 sin³20°)
= 2 sin(3 × 20)
= 2 sin 60°
= 2(\(\frac{\sqrt{3}}{2}\))
= √3

(ii) cos²72° – sin²54°
Solution:

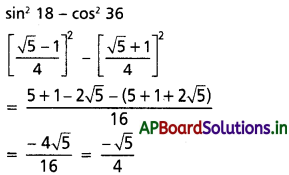
(iii) sin²42° – sin²12°
sin²42° – sin²12°
= sin(42° + 12°) sin(42° – 12°)
= sin 54° . sin 30°
= \(\left[\frac{\sqrt{5}+1}{4}\right] \frac{1}{2}\)
= \(\frac{\sqrt{5}+1}{8}\)

Question 3.
(i) \(\frac{\sin 4 \theta}{\sin \theta}\) ను cos³θ, cos θ పదాలలో రాయండి.
Solution:
sin 4θ = sin(3θ + θ)
= sin 3θ cos θ + cos 3θ sin θ
= (3 sin θ – 4 sin³θ) cos θ + (4 cos³θ – 3 cos θ) sin θ
= 3 sin θ cos θ – 4 sin³θ cos θ + 4 cos³θ sin θ – 3 cos θ sin θ
= 4 cos³θ sin θ – 4 sin³θ cos θ
= sin θ (4 cos³θ – 4 sin²θ cos θ)
\(\frac{\sin 4 \theta}{\sin \theta}=\frac{\sin \theta\left(4 \cos ^3 \theta-4 \sin ^2 \theta \cos \theta\right)}{\sin \theta}\)
= 4 cos³θ – 4(1 – cos²θ) cos θ
= 4 cos³θ – 4 cos θ + 4 cos³θ
= 8 cos³θ – 4 cos θ

(ii) cos⁶A + sin⁶A ను sin 2A పదాలలో రాయండి.
Solution:
cos⁶A + sin⁶A
= (cos²A)³ + (sin²A)³
= (cos²A + sin²A)³ – 3 cos²A sin²A (cos²A + sin²A)
= 1 – 3 cos²A sin²A
= 1 – \(\frac{3}{4}\) (4 cos²A sin²A)
= 1 – \(\frac{3}{4}\) sin²2A

(iii) \(\frac{1-\cos \theta+\sin \theta}{1+\cos \theta+\sin \theta}\) ను tan θ/2 పదాలలో రాయండి.
Solution:
\(\frac{1-\cos \theta+\sin \theta}{1+\cos \theta+\sin \theta}\)

Question 4.
(i) \(\frac{\pi}{2}\) < α < π, sin α = \(\frac{3}{5}\), అయితే cos 3α ను, tan 2α విలువలను గణించండి. [(T.S) Mar. ’15]
Solution:

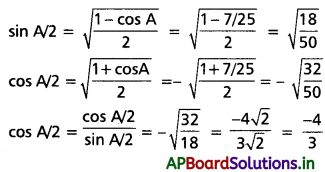
(ii) \(\frac{3 \pi}{2}\) < A < 2π, cos A = \(\frac{7}{25}\), అయితే cot A/2 విలువ కనుక్కోండి.
Solution:
cos A = \(\frac{7}{25}\)
ఇచ్చినవి \(\frac{3 \pi}{2}\) < A < 2π
⇒ \(\frac{3 \pi}{4}<\frac{A}{2}<\pi\)
∴ A, 4వ పాదంలో ఉంది మరియు \(\frac{A}{2}\) రెండవ పాదంలో ఉంది.

(iii) 0 < θ < \(\frac{\pi}{8}\), అయితే \(\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 4 \theta)}}}=2 \cos (\theta / 2)\) అని చూపండి.
Solution:

Question 5.
(i) cos 2x + cos²x లకు అంతిమ విలువలు కనుక్కోండి.
Solution:
cos 2x + cos²x = 2 cos²x – 1 + cos²x = 3 cos²x – 1
-1 ≤ cos x ≤ 1
0 ≤ cos²x ≤ 1
0 ≤ 3cos²x ≤ 3
-1 ≤ 3cos²x – 1 ≤ 2
గరిష్ట విలువ = 2, కనిష్ఠ విలువ = -1

(ii) 3 sin²x + 5 cos²x లకు అంతిమ విలువలు కనుక్కోండి.
Solution:
3 sin²x + 5 cos²x
= 3(1 – cos²x) + 5cos²x
= 3 – 3 cos²x + 5 cos²x
= 3 + 2 cos²x
-1 ≤ cos x ≤ 1
0 ≤ cos²x ≤ 1
0 ≤ 2 cos²x ≤ 2
3 ≤ 3 + 2 cos²x ≤ 5
గరిష్ఠ విలువ = 5, కనిష్ఠ విలువ = 3

Question 6.
a ≤ cos θ + 3√2 sin[θ + \(\frac{\pi}{4}\)] + 6 ≤ b a గరిష్ట విలువ, b కనిష్ఠ విలువలను కనుక్కోండి.
Solution:

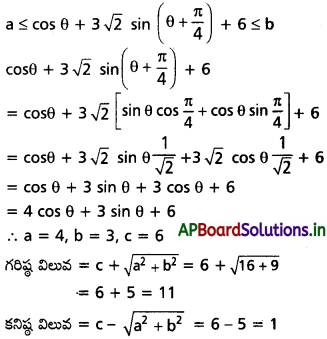
Question 7.
కింది ప్రమేయాల ఆవర్తనాలు కనుక్కోండి.
(i) cos⁴x
Solution:

(ii) \(2 \sin \left[\frac{\pi x}{4}\right]+3 \cos \left[\frac{\pi x}{3}\right]\)
Solution:

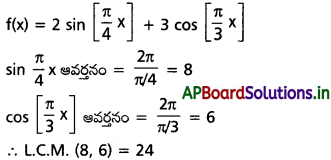
(iii) sin²x + 2cos²x
Solution:
Let f(x) = sin²x + 2cos²x
= 1 – cos²x + 2cos²x
= 1 + cos²x
= 1 + \(\frac{1+\cos 2 x}{2}\)
∴ cos 2x = \(\frac{2 \pi}{2}\) = π ఆవర్తనం
∴ f(x) = π ఆవర్తనం

(iv) 2sin[\(\frac{\pi}{4}\) + x] cos x
Solution:

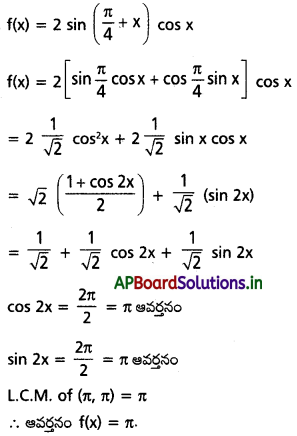
(v) \(\frac{5 \sin x+3 \cos x}{4 \sin 2 x+5 \cos x}\)
Solution:
Let f(x) = \(\frac{5 \sin x+3 \cos x}{4 \sin 2 x+5 \cos x}\)
sin x = 2π ఆవర్తనం
cos x = 2π ఆవర్తనం
sin 2x = \(\frac{2 \pi}{2}\) = π ఆవర్తనం
cos x = 2π ఆవర్తనం
L.C.M. of (2π, 2π, π‚ 2π) = 2π ఆవర్తనం
∴ f(x) = 2π ఆవర్తనం

II.

Question 1.
(i) 0 < A < \(\frac{\pi}{4}\), cos A = \(\frac{4}{5}\) అయితే sin 2A, cos 2A విలువలను కనుక్కోండి.
Solution:

(ii) \(\frac{\cot ^3 A-3 \cot A}{3 \cot ^2 A-1}\) ధనాత్మకం అయ్యేటట్లు ప్రథమ పాదంలోని A విలువలు కనుక్కోండి.
Solution:

(iii) \(\frac{\cos 3 A+\sin 3 A}{\cos A-\sin A}\) = 1 + 2 sin 2A అని చూపండి.
Solution:

Question 2.
(i) \(\cot \left[\frac{\pi}{4}-\theta\right]=\frac{\cos 2 \theta}{1-\sin 2 \theta}\) అని చూపి దాని నుంచి cot 15° విలువను రాబట్టండి.
Solution:

(ii) sin θ = \(\frac{-4}{5}\), θ మూడవ పాదంలోకి కోణం అయితే cosec(θ/2), tan(θ/2) ల విలువలు కనుక్కోండి.
Solution:

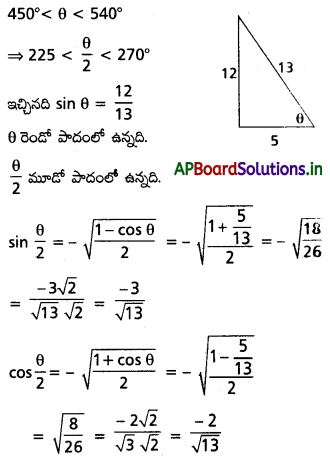
(iii) 450°< θ < 540°, sin θ = \(\frac{12}{13}\), అయితే sin(θ/2), cos(θ/2) ల విలువలను కనుక్కోండి.
Solution:

(iv) \(\frac{1}{\cos 290^{\circ}}+\frac{1}{\sqrt{3} \sin 250^{\circ}}=\frac{4}{\sqrt{3}}\) అని చూపండి.
Solution:

Question 3.
కింది వాటిని నిరూపించండి.
(i) \(\frac{\sin 2 A}{(1-\cos 2 A)} \cdot \frac{(1-\cos A)}{\cos A}=\tan \frac{A}{2}\)
Solution:

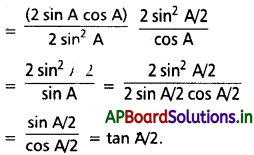
(ii) \(\frac{\sin 2 x}{(\sec x+1)} \cdot \frac{\sec 2 x}{(\sec 2 x+1)}=\tan \left[\frac{x}{2}\right]\)
Solution:

(iii) \(\frac{\left(\cos ^3 \theta-\cos 3 \theta\right)}{\cos \theta}+\frac{\left(\sin ^3 \theta+\sin 3 \theta\right)}{\sin \theta}=3\)
Solution:

Question 4.
(i) cos A = \(\frac{\cos 3 A}{(2 \cos 2 A-1)}\) అని చూపి, దాని నుంచి cos 15° విలువను కనుక్కోండి.
Solution:

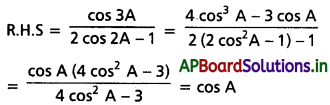
(ii) sin A = \(\frac{\sin 3 A}{1+2 \cos 2 A}\) అని చూపి, దాని నుంచి sin 15° విలువను కనుక్కోండి.
Solution:

(iii) tan α = \(\frac{\sin 2 \alpha}{1+\cos 2 \alpha}\) అని చూపి, దాని నుంచి tan 15°, tan 22\(\frac{1^{\circ}}{2}\) ల విలువలను కనుక్కోండి.
Solution:

Question 5.
కింది వాటిని నిరూపించండి.
(i) \(\frac{1}{\sin 10^{\circ}}-\frac{\sqrt{3}}{\cos 10^{\circ}}=4\) [June ’04]
Solution:

(ii) √3 cosec 20° – sec 20° = 4
Solution:
L.H.S. = √3 cosec 20° – sec 20°
= \(\frac{\sqrt{3}}{\sin 20}-\frac{1}{\cos 20}\)

(iii) tan 9° – tan 27° – cot 27° + cot 9° = 4.
Solution:

(iv) \(\frac{\sin \alpha}{a}=\frac{\cos \alpha}{b}\) అయితే a sin 2α + b cos 2α = b.
Solution:
ఇచ్చినది \(\frac{\sin \alpha}{a}=\frac{\cos \alpha}{b}\)
⇒ b sin α = a cos α
L.H.S. = a sin 2α + b cos 2α
= a 2 sin α cos α + b(1 – 2 sin²α)
= 2 sin α (a cos α) + b – 2b sin²α
= 2 sin α (b sin α) + b – 2b sin²α
= 2b sin²α + b – 2b sin²α
= b

Question 6.
(i) ABC త్రిభుజంలో \(\tan \frac{A}{2}=\frac{5}{6}, \tan \frac{B}{2}=\frac{20}{37}\) అయితే, \(\tan \left[\frac{C}{2}\right]=\frac{2}{5}\) అని చూపండి.
Solution:

(ii) cos θ = \(\frac{5}{13}\), 270° < θ < 360° అయితే, sin(θ/2), cos(θ/2) లను గణించండి.
Solution:

(iii) 180°< θ < 270°, sin θ = \(\frac{-4}{5}\) అయితే, sin(θ/2), cos(θ/2) లను గణించండి.
Solution:

Question 7.
(i) \(\cos ^2 \frac{\pi}{8}+\cos ^2 \frac{3 \pi}{8}+\cos ^2 \frac{5 \pi}{8}+\cos ^2 \frac{7 \pi}{8}\) = 2 అని నిరూపించండి.
Solution:

(ii) \(\cos ^4\left(\frac{\pi}{8}\right)+\cos ^4\left(\frac{3 \pi}{8}\right)+\cos ^4\left(\frac{5 \pi}{8}\right)+\cos ^4\left(\frac{7 \pi}{8}\right)\) = \(\frac{3}{2}\) అని చూపండి.
Solution:

III.

Question 1.
(i) \(\tan x+\tan \left(x+\frac{\pi}{3}\right)+\tan \left(x+\frac{2 \pi}{3}\right)=3\), అయితే tan 3x = 1 అని చూపండి.
Solution:

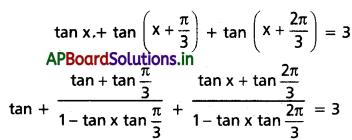
(ii) \(\sin \frac{\pi}{5} \cdot \sin \frac{2 \pi}{5} \cdot \sin \frac{3 \pi}{5} \cdot \sin \frac{4 \pi}{5}=\frac{5}{16}\) అని నిరూపించండి. [Mar. ’13]
Solution:

(iii) \(\cos ^2\left(\frac{\pi}{10}\right)+\cos ^2\left(\frac{2 \pi}{5}\right)+\cos ^2\left(\frac{3 \pi}{5}\right)\) + \(\cos ^2\left(\frac{9 \pi}{10}\right)\) = 2 అని చూపండి.
Solution:

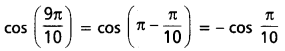
Question 2.
కింది వాటిని నిరూపించండి.
(i) \(\frac{1-\sec 8 \alpha}{1-\sec 4 \alpha}=\frac{\tan 8 \alpha}{\tan 2 \alpha}\)
Solution:

(ii) \(\left[1+\cos \frac{\pi}{10}\right]\left[1+\cos \frac{3 \pi}{10}\right]\left[1+\cos \frac{7 \pi}{10}\right]\) \(\left[1+\cos \frac{9 \pi}{10}\right]=\frac{1}{16}\) [(AP) Mar. ’15]
Solution:
\(\left(1+\cos \frac{\pi}{10}\right)\left(1+\cos \frac{3 \pi}{10}\right)\left(1+\cos \frac{7 \pi}{10}\right)\)

Question 3.
కింది వాటిని నిరూపించండి.
(i) \(\cos \frac{2 \pi}{7} \cdot \cos \frac{4 \pi}{7} \cdot \cos \frac{8 \pi}{7}\) = \(\frac{1}{8}\)
Solution:

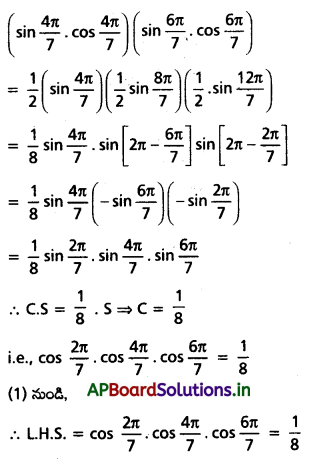
(ii) \(\cos \frac{\pi}{11} \cdot \cos \frac{2 \pi}{11} \cdot \cos \frac{3 \pi}{11} \cdot \cos \frac{4 \pi}{11} \cdot \cos \frac{5 \pi}{11}\) = \(\frac{1}{32}\)
Solution:

Question 4.
(i) α, β లు లఘు కోణాలు, cos α = \(\frac{3}{5}\), cos β = \(\frac{5}{13}\) అయితే, (a) \(\sin ^2\left(\frac{\alpha-\beta}{2}\right)=\frac{1}{65}\) (b) \(\cos ^2\left(\frac{\alpha+\beta}{2}\right)=\frac{16}{65}\) అని చూపండి.
Solution:

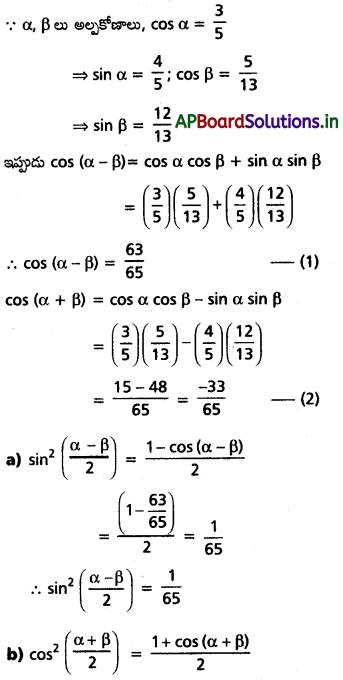
(ii) A అనేది π యొక్క పూర్ణాంక గుణిజం కాకపోతే, cos A . cos 2A . cos 4A . cos 8A = \(\frac{\sin 16 A}{16 \sin A}\) అని నిరూపించండి. దీని నుంచి \(\cos \frac{2 \pi}{15} \cdot \cos \frac{4 \pi}{15} \cdot \cos \frac{8 \pi}{15} \cdot \cos \frac{16 \pi}{15}=\frac{1}{16}\) అని చూపండి. [May ’13; Mar. ’12]
Solution:
16 sin A {cos A . cos 2A . cos 4A . cos 8A}
= 8(2 sin A . cos A) cos 2A . cos 4A . cos 8A
= 8 sin 2A . cos 2A . cos 4A . cos 8A
= 4(2 sin 2A . cos 2A) . cos 4A . cos 8A
= 4 sin 4A . cos 4A . cos 8A
= 2(2 sin 4A . cos 4A) . cos 8A
= 2 sin 8A . cos 8A
= sin(16A)
∴ 16 sin A {cos A . cos 2A . cos 4A . cos 8A} = sin(16A)
∴ cos A . cos 2A . cos 4A . cos 8A = \(\frac{\sin 16 A}{16 \sin A}\)