AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(e)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(e) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(e)

I.

Question 1.
sin 50° – sin 70° + sin 10° = 0 అని నిరూపించండి.
Solution:
L.H.S = sin 50° – sin 70° + sin 10°
= 2 cos\(\left(\frac{50^{\circ}+70^{\circ}}{2}\right)\) sin\(\left(\frac{50^{\circ}-70^{\circ}}{2}\right)\) + sin 10°
= 2 cos 60° . sin(-10°) + sin 10°
= 2(\(\frac{1}{2}\)) (-sin 10°) + sin 10°
= -sin 10° + sin 10°
= 0
∴ sin 50° – sin 70° + sin 10° = 0

Question 2.
\(\frac{\sin 70^{\circ}-\cos 40^{\circ}}{\cos 50^{\circ}-\sin 20^{\circ}}=\frac{1}{\sqrt{3}}\) అని నిరూపించండి.
Solution:

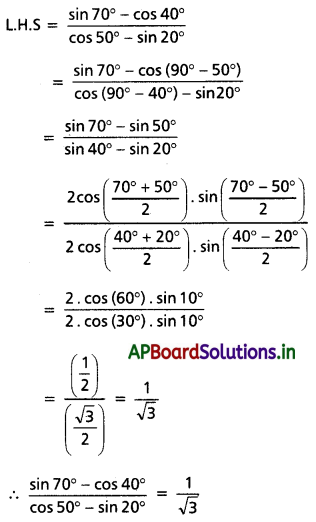
Question 3.
cos 55° + cos 65° + cos 175° = 0 అని రుజువు చేయండి.
Solution:
L.H.S = cos 55° + cos 65° + cos 175°
= cos 65° + cos 55° + cos(180° – 5°)
= 2 cos\(\left(\frac{65^{\circ}+55^{\circ}}{2}\right)\) . cos\(\left(\frac{65^{\circ}-55^{\circ}}{2}\right)\) – cos 5°
= 2 cos (60°) . cos (5°) – cos 5°
= 2(\(\frac{1}{2}\)) cos 5° – cos 5°
= cos 5° – cos 5°
= 0
∴ cos 55° + cos 65° + cos 175° = 0

Question 4.
4(cos 66° + sin 84°) = √3 + √15 అని నిరూపించండి.
Solution:
LHS = 4(cos 66° + sin 84°)
= 4[cos 66° + sin (90° – 6°)]
= 4[cos 66° + cos 6°]
= \(4\left[2 \cdot \cos \left(\frac{66^{\circ}+6^{\circ}}{2}\right) \cdot \cos \left(\frac{66^{\circ}-6^{\circ}}{2}\right)\right]\)
= 8 . cos 30° . cos 36°
= \(8 \cdot\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{5}+1}{4}\right)\)
= √3(√5 + 1)
= √3 + √15
∴ 4(cos 66°+ sin 84°) = √3 + √15

Question 5.
cos 20° cos 40° – sin 5° sin 25° = \(\frac{\sqrt{3}+1}{4}\) అని రుజువు చేయండి.
Solution:
cos 20° cos 40° – sin 5° sin 25°
= \(\frac{1}{2}\) [2 cos 20° cos 40° – 2 sin 5° sin 25°]
= \(\frac{1}{2}\) [cos(20° + 40°) + cos(20° – 40°) – {cos (5° – 25°) cos (5° + 25°)}]
= \(\frac{1}{2}\) [cos 60° + cos 20° – cos 20° + cos 30°]
= \(\frac{1}{2}\left[\frac{1}{2}+\frac{\sqrt{3}}{2}\right]\)
= \(\frac{\sqrt{3}+1}{4}\)
∴ cos 20° cos 40° – sin 5° sin 25° = \(\frac{\sqrt{3}+1}{4}\)

Question 6.
cos 48° . cos 12° = \(\frac{3+\sqrt{5}}{8}\) అని నిరూపించండి.
Solution:
L.H.S = cos 48° . cos 12°
= \(\frac{1}{2}\) (2 cos 48° . cos 12°)
= \(\frac{1}{2}\) [cos (48° + 12°) + cos (48° – 12°)]
= \(\frac{1}{2}\) [cos 60° + cos 36°]
= \(\frac{1}{2}\left[\frac{1}{2}+\frac{\sqrt{5}+1}{4}\right]\)
= \(\frac{1}{2}\left[\frac{2+\sqrt{5}+1}{4}\right]\)
= \(\frac{3+\sqrt{5}}{8}\)
∴ cos 48° . cos 12° = \(\frac{3+\sqrt{5}}{8}\)

II.

Question 1.
cos θ + cos[\(\frac{2 \pi}{3}\) + θ] + cos[\(\frac{4 \pi}{3}\) + θ] = 0 అని చూపండి.
Solution:
LHS = cos θ + cos(120° + θ) + cos(240° + θ)
= cos θ + {cos 120° cos θ – sin 120° sin θ} + {cos 240° cos θ – sin 240° . sin θ}

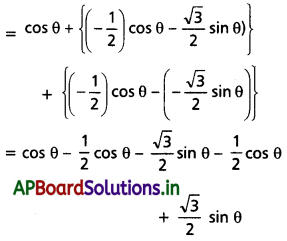
= cos θ – cos θ
= 0
∴ cos θ + cos(120° + θ) + cos(240° + θ) = 0

Question 2.
sin²(α – π/4) + sin²(α + π/2) – sin²(α – π/2) = \(\frac{1}{2}\) అని చూపండి.
Solution:

Question 3.
sin x + sin y = \(\frac{1}{y}\), cos x + cos y = \(\frac{1}{3}\) అయితే (i) \(\tan \left(\frac{x+y}{2}\right)=\frac{3}{4}\) (ii) cot(x + y) = \(\frac{7}{24}\) అని చూపండి.
Solution:

Question 4.
\(\left[A-\frac{\pi}{12}\right] \cdot\left[A-\frac{5 \pi}{12}\right]\) అనేవి π కి పూర్ణాంక గుణిజం కాకపొతే cot(π/2 – A) + tan(π/12 + A) = \(\frac{4 \cos 2 A}{1-2 \sin 2 A}\) అని నిరూపించండి.
Solution:

Question 5.
4 cos 12° cos 48° cos 72° = cos 36° అని నిరూపించండి.
Solution:
L.H.S. = 4 cos 12° cos 48° cos 72°
= 2 cos 12° {2 cos 72° cos 48°}
= 2 cos 12° {cos(72° + 48°) + cos(72° – 48°)}
= 2 cos 12° {cos(120°) + cos 24°}
= 2 cos 12° {\(-\frac{1}{2}\) + cos 24°}
= 2 cos 12° \(\left\{\frac{-1+2 \cos 24^{\circ}}{2}\right\}\)
= -cos 12° + 2 cos 24° cos 12°
= -cos 12° + {cos(24° + 12°) + cos(24° – 12°)}
= -cos 12° + cos 36° + cos 12°
= cos 36°
∴ 4 cos 12° cos 48° cos 72° = cos 36°

Question 6.
sin 10° + sin 20° + sin 40° + sin 50° = sin 70° + sin 80° అని నిరూపించండి.
Solution:
L.H.S. = sin 10° + sin 20° + sin 40° + sin 50°
= (sin 50°+ sin 10°) + (sin 40° + sin 20°)
= 2 sin\(\left(\frac{50^{\circ}+10^{\circ}}{2}\right)\) . cos\(\left(\frac{50^{\circ}-10^{\circ}}{2}\right)\) + 2 sin\(\left(\frac{40^{\circ}+20^{\circ}}{2}\right)\) . cos\(\left(\frac{40^{\circ}-20^{\circ}}{2}\right)\)
= 2 sin 30° . cos 20° + 2 sin 30° . cos 10°
= 2 sin 30° (cos 20° + cos 10°)
= 2(\(\frac{1}{2}\)) [cos(90° – 70°) + cos(90° – 80°)]
= sin 70° + sin 80°
∴ sin 10° + sin 20° + sin 40° + sin 50° = sin 70° + sin 80°

III.

Question 1.
cos x + cos y = \(\frac{4}{5}\), cos x – cos y = \(\frac{2}{7}\) అయితే \(14 \tan \frac{x-y}{2}+5 \cot \frac{x+y}{2}\) విలువను కనుక్కోండి.
Solution:

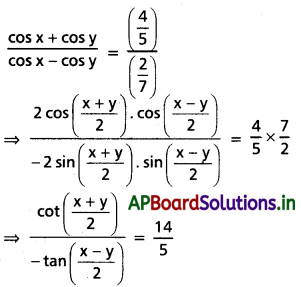
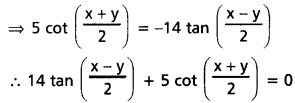
Question 2.
కింది సమీకరణంలో హారాలు సున్నా కానప్పుడు,

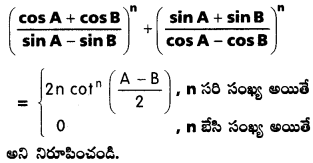
Solution:

Question 3.
sin A = sin B, cos A = cos B అయితే A = 2nπ + B (n ∈ Z) అని చూపండి.
Solution:

Question 4.
cos nα ≠ 0, cos \(\frac{\alpha}{2}\) ≠ 0 అయితే \(\frac{\sin (n+1) \alpha-\sin (n-1) \alpha}{\cos (n+1) \alpha+2 \cos n \alpha+\cos (n-1) \alpha}\) = tan \(\frac{\alpha}{2}\) అని చూపండి.
Solution:

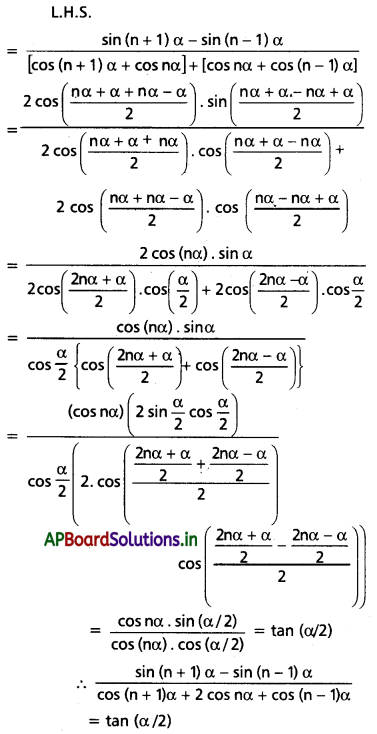
Question 5.
sec(θ + α) + sec(θ – α) = 2 sec θ, cos α ≠ 1 అయితే, cos θ = ±√2 cos α/2 అని చూపండి.
Solution:
cos α ≠ 1,
sec(θ + α) + sec(θ – α) = 2 sec θ
⇒ \(\frac{1}{\cos (\theta+\alpha)}+\frac{1}{\cos (\theta-\alpha)}=\frac{2}{\cos \theta}\)
⇒ \(\frac{\cos (\theta-\alpha)+\cos (\theta+\alpha)}{\cos (\theta+\alpha) \cdot \cos (\theta-\alpha)}=\frac{2}{\cos \theta}\)
⇒ \(\frac{2 \cos \theta \cdot \cos \alpha}{\cos ^2 \theta-\sin ^2 \alpha}=\frac{2}{\cos \theta}\)
⇒ cos²θ cos α = cos²θ – sin²α
⇒ cos²θ (cos α – 1) = -sin²α
⇒ cos²θ (1 – cos α) = sin²α
⇒ cos²θ (1 – cos α) = 1 – cos²α
⇒ cos²θ = 1 + cos α, [∵ cos α ≠ 1]
⇒ cos²θ = 2 cos²(α/2)
∴ cos θ = ±√2 cos(α/2)

Question 6.
x, y, z లు ఏవీ \(\frac{\pi}{2}\) బేసి గుణిజాలు కాకపోయి, sin(y + z – x), sin(z + x – y), sin(x + y – z) లు అంకశ్రేఢిలో ఉంటే, tan x, tan y, tan z లు కూడా అంకశ్రేఢిలో ఉంటాయని చూపండి.
Solution:
sin(y + z – x), sin(z + x – y), sin(x + y – z) లు A.P. లో ఉన్నవి.
⇒ sin(z + x – y) – sin(y + z – x) = sin(x + y – z) – sin(z + x – y)
⇒ 2 cos z sin(x – y) = 2 cos x sin(y – z)
⇒ cos z [sin x cos y – cos x sin y] = cos x [sin y cos z – cos y sin z]
cos x, cos y, cos z చే భాగించగా
⇒ \(\frac{\sin x}{\cos x}-\frac{\sin y}{\cos y}=\frac{\sin y}{\cos y}-\frac{\sin z}{\cos z}\)
⇒ tan x – tan y = tan y – tan z
⇒ tan x + tan z = 2 tan y
∴ tan x, tan y, tan z లు A.P. లో వున్నాయి.

Question 7.
x, y, z ∈ R – {0}, x cos θ = y cos(θ + \(\frac{2 \pi}{3}\)) = z cos(θ + \(\frac{4 \pi}{3}\)), θ ∈ R అయితే xy + yz + zx = 0 అని చూపండి.
Solution:
x ≠ 0, y ≠ 0, z ≠ 0,
x cos θ = y cos(θ + \(\frac{2 \pi}{3}\)) = z cos(θ + \(\frac{4 \pi}{3}\)) = λ అనుకుంటే

Question 8.
A, A + B లు \(\frac{\pi}{2}\) బేసి గుణిజాలు కావు, m sin B = n sin(2A + B) అయితే (m + n) tan A = (m – n) tan(A + B) అని చూపండి.
Solution:
A, (A + B) లు \(\frac{\pi}{2}\) బేసి గుణిజాలు కావు.

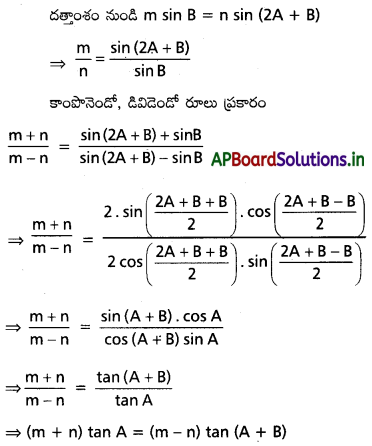
Question 9.
tan(A + B) = λ tan(A – B) అయితే, (λ + 1) sin 2B = (λ – 1) sin 2A అని చూపండి.
Solution: