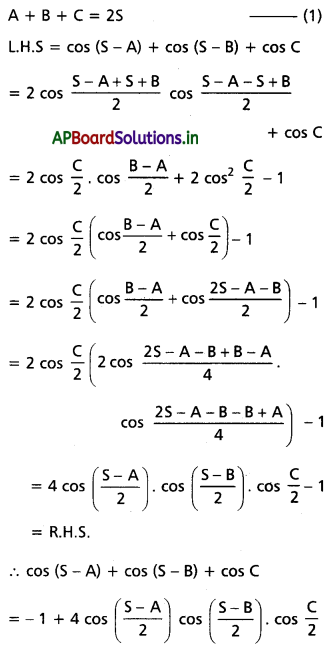AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f)

by

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(f) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(f)

Question 1.
A, B, C లు త్రిభుజ కోణాలయితే, కింది వాటిని రుజువు చేయండి.
(i) sin 2A – sin 2B + sin 2C = 4 cos A sin B cos C
Solution:
∵ A, B, C లు త్రిభుజ కోణాలు, కాబట్టి
A + B + C = 180° ………(1)
L.H.S. = sin 2A – sin 2B + sin 2C
= sin 2A + sin 2C – sin 2B
= 2 sin\(\left(\frac{2 A+2 C}{2}\right)\) . cos\(\left(\frac{2 A-2 C}{2}\right)\) – sin 2B
= 2 sin(A + C) cos(A – C) – sin 2B
= 2 sin(180° – B) cos(A – C) – 2 sin B cos B
= 2 sin B cos(A – C) – 2 sin B cos B
= 2 sin B [cos(A – C) – cos B]
= 2 sin B [cos(A – C) cos (180° – (A + C)]
=2 sin B [cos(A – C) + cos(A + C)]
= 2 sin B (2 cos A cos C)
= 4 cos A sin B cos C
∴ sin 2A – sin 2B + sin 2C = 4 cos A sin B cos C

(ii) cos 2A – cos 2B + cos 2C = 1 – 4 sin A cos B sin C
Solution:
L.H.S. = -(cos 2B – cos 2A) + cos 2C
= -2 sin(A + B) sin(A – B) + cos 2C
= -2 sin(180° – C) sin(A – B) + cos 2C
= -2 sin C sin(A – B) + 1 – 2 sin2C
= 1 – 2 sinC (sin(A – B) + sin C)
= 1 – 2 sin C (sin(A – B) + sin(180° – \(\overline{A+B}\))
= 1 – 2 sin C (sin(A – B) + sin(A + B))
= 1 – 2 sin C (2 sin A cos B)
= 1 – 4 sin A cos B sin C
= R.H.S.

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f)

Question 2.
A, B, C లు త్రిభుజం కోణాలయితే, కింది వాటిని రుజువు చేయండి.
(i) sin A + sin B – sin C = \(4 \sin \frac{A}{2} \sin \frac{B}{2} \cos \frac{C}{2}\)
Solution:
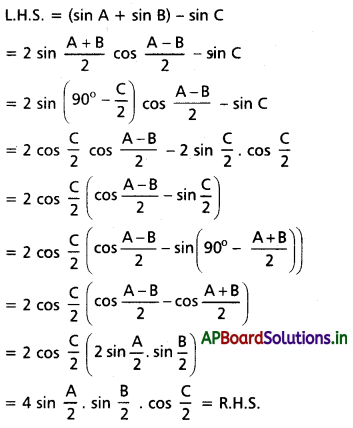
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q2(i)

(ii) cos A + cos B – cos C = -1 + \(4 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\) [May ’06]
Solution:
A, B, C లు త్రిభుజ కోణాలు, కాబట్టి
A + B + C = 180° ………(1)
L.H.S. = cos A + cos B – cos C
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q2(ii)
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q2(ii).1

Question 3.
A, B, C లు త్రిభుజ కోణాలయితే, కింది వాటిని రుజువు చేయండి.
(i) sin2A + sin2B – sin2C = 2 sin A sin B cos C
Solution:
A + B + C = 180°
L.H.S. = sin2A + [sin2B – sin2C]
= sin2A + sin(B + C) sin(B – C)
= sin2A + sin(180° – A) . sin(B – C)
= sin2A + sin A . sin(B – C)
= sin A (sin A + sin(B – C))
= sin A [sin(180° – \(\overline{B+C}\)) + sin(B – C)]
= sin A [sin(B + C) + sin(B – C)]
= sin A [2 sin B cos C]
= 2 sin A sin B cos C
= R.H.S.

(ii) cos2A + cos2B – cos2C = 1 – 2 sin A sin B cos C
Solution:
A, B, C లు త్రిభుజ కోణాలు
A + B + C = 180° ……..(1)
L.H.S. = cos2A + cos2B – cos2C
= cos2A + cos2B – cos2C
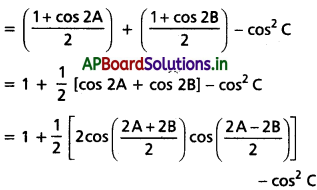
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q3(ii)
= 1 + cos(A + B) cos(A – B) – cos2C
= 1 + cos(180° – C) cos(A – B) – cos2C [(1) నుండి]
= 1 – cos C cos(A – B) – cos2C
= 1 – cos C [cos(A – B) + cos C]
= 1 – cos C [cos(A – B) + cos(180° – \(\overline{A+B}\))] (సమీ. (1) నుండి)
= 1 – cos C [cos(A – B) – cos(A + B)]
= 1 – cos C [2 sin A sin B]
= 1 – 2 sin A sin B cos C
∴ cos2A + cos2B – cos2C = 1 – 2 sin A sin B cos C

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f)

Question 4.
A + B + C = π అయితే కింది ఫలితాలు రుజువు చేయండి. [(A.P & T.S) Mar. ’12, Mar. ’15]
(i) \(\cos ^2 \frac{A}{2}+\cos ^2 \frac{B}{2}+\cos ^2 \frac{C}{2}=2\) \(\left[1+\sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}\right]\)
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q4(i)

(ii) \(\cos ^2 \frac{A}{2}+\cos ^2 \frac{B}{2}-\cos ^2 \frac{C}{2}\) = \(2 \cos \frac{A}{2} \cdot \cos \frac{B}{2} \sin \frac{C}{2}\)
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q4(ii)

Question 5.
ABC త్రిభుజంలో, కింది వాటిని రుజువు చేయండి.
(i) \(\cos \frac{A}{2}+\cos \frac{B}{2}+\cos \frac{C}{2}\) = \(4 \cos \frac{\pi-A}{4} \cos \frac{\pi-B}{4} \cos \frac{\pi-C}{4}\) [May ’13]
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q5(i)
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q5(i).1
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q5(i).2

(ii) \(\cos \frac{A}{2}+\cos \frac{B}{2}-\cos \frac{C}{2}\) = \(4 \cos \frac{\pi+A}{4} \cdot \cos \frac{\pi+B}{4} \cdot \cos \frac{\pi-C}{4}\) [Mar. ’05]
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q5(ii)
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q5(ii).1

(iii) \(\sin \frac{A}{2}+\sin \frac{B}{2}-\sin \frac{C}{2}\) = \(1+4 \cos \frac{\pi-A}{4} \cos \frac{\pi-B}{4} \sin \frac{\pi-C}{4}\)
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q5(iii)
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q5(iii).1
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q5(iii).2

Question 6.
A + B + C = π/2 అయితే cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C అని చూపండి.
Solution:
A + B + C = π/2 ……..(1)
L.H.S = cos 2A + cos 2B + cos 2C
= 2 cos\(\left(\frac{2 A+2 B}{2}\right)\) cos\(\left(\frac{2 A-2 B}{2}\right)\) + cos 2C
= 2 cos(A + B) . cos(A – B) + cos 2C
= 2 cos(π/2 – C) cos(A – B) + cos 2C
= 2 sin C cos(A – B) + (1 – 2 sin2C)
= 1 + 2 sin C [cos(A – B) – sin C]
= 1 + 2 sin C [cos(A – B) sin(π/2 – \(\overline{A+B}\))]
= 1 + 2 sin C [cos(A – B) – cos(A + B)]
= 1 + 2 sin C [2 sin A sin B]
= 1 + 4 sin A sin B sin C
∴ cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f)

Question 7.
A + B + C = 3π/2 అయితే, కింది వాటిని ఋజువు చేయండి.
(i) cos2A + cos2B – cos2C = -2 cos A cos B sin C
Solution:
A + B + C = 3π/2 ……..(1)
L.H.S. = cos2A + cos2B – cos2C
= cos2A + (1 – sin2B) – cos2C
= (cos2A – sin2B) + (1 – cos2C)
= cos(A + B) cos(A – B) + sin2C
= cos(3π/2 – C) cos(A – B) + sin2C
= -sin C cos(A – B) + sin2C
= sin C [sin C – cos(A – B)]
= sin C [sin(270° – \(\overline{A+B}\)) – cos(A – B)]
= sin C [-cos(A + B) – cos(A – B)]
= -sin C [cos(A + B) + cos(A – B)]
= -sin C [2 cos A cos B]
= -2 cos A cos B sin C
∴ cos2A + cos2B – cos2C = -2 cos A cos B sin C

(ii) sin 2A + sin 2B – sin 2C = -4 sin A sin B cos C
Solution:
A + B + C = 270° …….(1)
L.H.S = sin 2A + sin 2B – sin 2C
= 2 sin\(\left(\frac{2 A+2 B}{2}\right)\) cos\(\left(\frac{2 A-2 B}{2}\right)\) – sin 2C
= 2 sin(A + B) . cos(A – B) – 2 sin C cos C
= 2 sin(270° – C) cos(A – B) – 2 sin C cos C
= -2 cos C cos(A – B) – 2 sin C cos C
= -2 cos C [cos(A – B) + sin C]
= -2 cos C [cos(A – B) + sin(270° – \(\overline{A+B}\))]
= -2 cos C [cos(A – B) – cos(A + B)]
= -2 cos C (2 sin A sin B)
= -4 sin A sin B cos C
∴ sin 2A + sin 2B – sin 2C = -4 sin A sin B cos C

Question 8.
A + B + C = 0 అయితే, కింది వాటిని ఋజువు చేయండి.
(i) sin 2A + sin 2B + sin 2C = -4 sin A sin B sin C
Solution:
A + B + C = 0 …….(1)
L.H.S.= sin 2A + sin 2B + sin 2C
= 2 sin\(\left(\frac{2 A+2 B}{2}\right)\) cos\(\left(\frac{2 A-2 B}{2}\right)\) + sin 2C
= 2 sin(A + B) cos (A – B) + 2 sin C cos C
= 2 sin(-C) cos(A – B) + 2 sin C cos C
= -2 sin C cos(A – B) + 2 sin C cos C
= -2 sin C [cos(A – B) – cos C]
= -2 sin C [cos(A – B) – cos(-A – B))
= -2 sin C [cos(A – B) – cos (A + B)]
= -2 sin C [2 sin A sin B]
= -4 sin A sin B sin C
∴ sin 2A + sin 2B + sin 2C = -4 sin A sin B sin C

(ii) sin A + sin B – sin C = \(-4 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\)
Solution:
A + B + C = 0°
L.H.S = sin A + sin B – sin C
= \(2 \sin \left(\frac{A+B}{2}\right) \cdot \cos \left(\frac{A-B}{2}\right)-\sin C\)
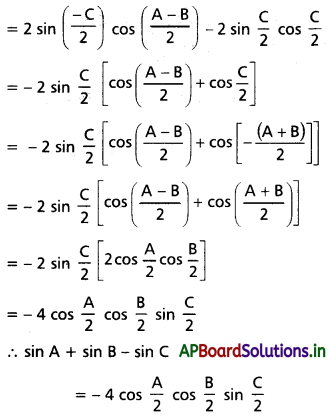
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q8(ii)

Question 9.
A + B + C + D = 2π అయితే, కింది వాటిని రుజువు చేయండి.
(i) sin A – sin B + sin C – sin D = \(-4 \cos \frac{A+B}{2} \sin \frac{A+C}{2} \cos \frac{A+D}{2}\)
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q9(i)
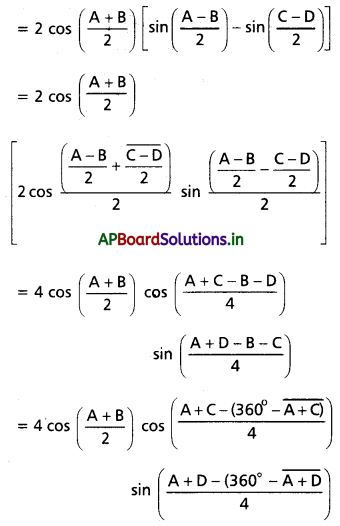
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q9(i).1
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q9(i).2

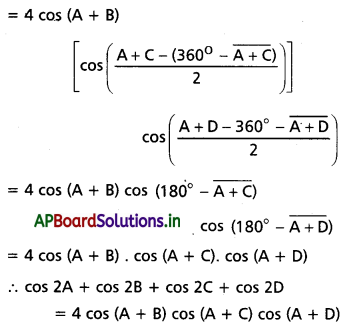
(ii) cos 2A + cos 2B + cos 2C + cos 2D = 4 cos(A + B) cos(A + C) cos(A + D)
Solution:
A + B + C + D = 360° …….(1)
L.H.S = cos 2A + cos 2B + cos 2C + cos 2D
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q9(ii)
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q9(ii).1

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f)

Question 10.
A + B + C = 2S అయితే, కింది వాటిని రుజువు చేయండి.
(i) sin(S – A) + sin(S – B) + sin C = \(4 \cos \frac{S-A}{2} \cos \frac{S-B}{2} \sin \frac{C}{2}\)
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q10(i)
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q10(i).1

(ii) cos(S – A) + cos(S – B) + cos C = \(-1+4 \cos \frac{S-A}{2} \cos \frac{S-B}{2} \cos \frac{C}{2}\)
Solution:
AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(f) I Q10(ii)