AP Inter 1st Year Maths 1A Solutions Chapter 8 విలోమ త్రికోణమితీయ ప్రమేయాలు Ex 8(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 8 విలోమ త్రికోణమితీయ ప్రమేయాలు Exercise 8(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 8 విలోమ త్రికోణమితీయ ప్రమేయాలు Exercise 8(a)

I.

Question 1.
క్రింది వాటి విలువలను కనుక్కోండి.
(i) \(\sin ^{-1}\left(\frac{-\sqrt{3}}{2}\right)\)
Solution:

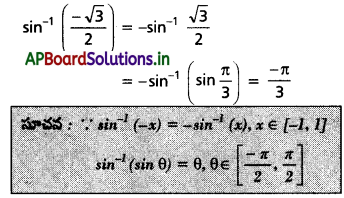
(ii) \(\cos ^{-1}\left(\frac{1}{\sqrt{2}}\right)\)
Solution:

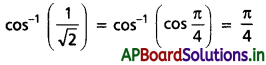
(iii) sec^-1(-√2)
Solution:

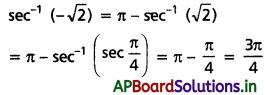
(iv) cot^-1(-√3)
Solution:

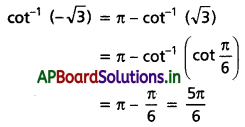
(v) \(\sin \left(\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right)\)
Solution:

(vi) \(\sin ^{-1}\left(\sin \left(\frac{5 \pi}{6}\right)\right)\)
Solution:

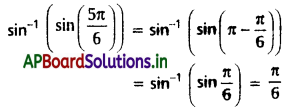
(vii) \(\cos ^{-1}\left(\cos \frac{5 \pi}{4}\right)\)
Solution:

Question 2.
క్రింది వాటి విలువలు కనుక్కోండి.
(i) \(\sin \left(\cos ^{-1} \frac{3}{5}\right)\)
Solution:

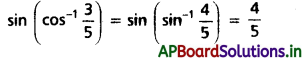
(ii) \(\tan \left({cosec}^{-1} \frac{65}{63}\right)\)
Solution:

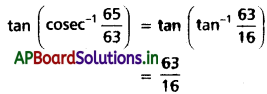
(iii) \(\sin \left(2 \sin ^{-1} \frac{4}{5}\right)\)
Solution:

(iv) \(\sin ^{-1}\left(\sin \frac{33 \pi}{7}\right)\)
Solution:

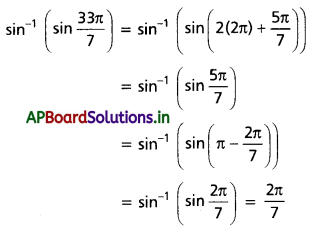
(v) \(\cos ^{-1}\left(\cos \frac{17 \pi}{6}\right)\)
Solution:

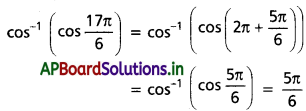
Question 3.
క్రింది వాటిని సూక్ష్మీకరించండి.
(i) \(\tan ^{-1}\left[\frac{\sin x}{1+\cos x}\right]\)
Solution:

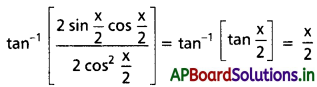
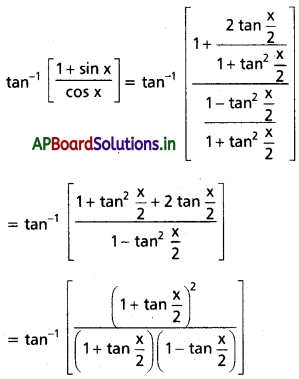
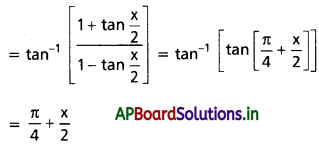
(ii) tan^-1(sec x + tan x)
Solution:

(iii) \(\tan ^{-1} \sqrt{\frac{1-\cos x}{1+\cos x}}\)
Solution:

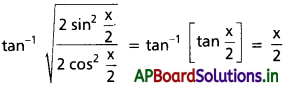
(iv) sin^-1(2 cos²θ – 1) + cos^-1(1 – 2 sin²θ)
Solution:
sin^-1(cos 2θ) + cos^-1(cos 2θ)
= sin^-1[sin(90° – 2θ°)] + cos^-1(cos 2θ)
= 90° – 2θ° + 2θ°
= 90°

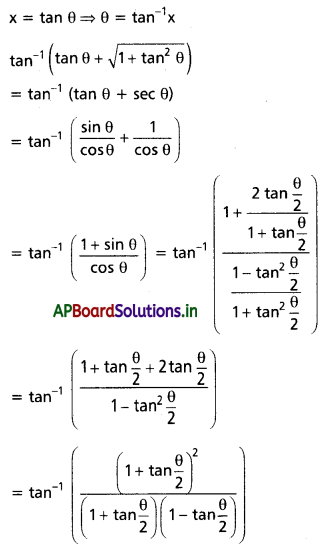
(v) \(\tan ^{-1}\left(x+\sqrt{1+x^2}\right)\); x ∈ R
Solution:

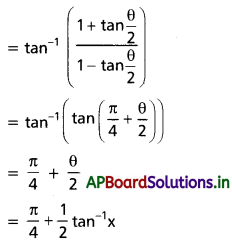
II.

Question 1.
క్రింది వాటిని రుజువు చేయండి.
(i) \(\sin ^{-1} \frac{3}{5}+\sin ^{-1} \frac{8}{17}=\cos ^{-1}\left(\frac{36}{85}\right)\) [May ’12]
Solution:

(ii) \(\sin ^{-1} \frac{3}{5}+\cos ^{-1} \frac{12}{13}=\cos ^{-1} \frac{33}{65}\)
Solution:

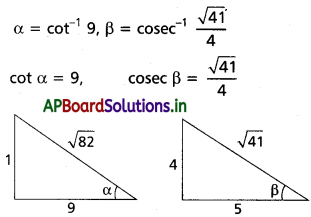
(iii) \(\tan \left[\cot ^{-1} 9+{cosec}^{-1} \frac{\sqrt{41}}{4}\right]=1\)
Solution:

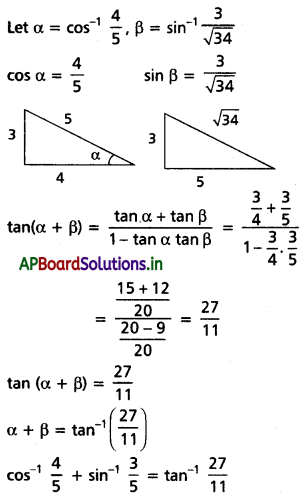
(iv) \(\cos ^{-1} \frac{4}{5}+\sin ^{-1} \frac{3}{\sqrt{34}}=\tan ^{-1} \frac{27}{11}\) [May ’13]
Solution:

Question 2.
క్రింది వాటి విలువలను కనుక్కోండి.
(i) \(\sin \left(\cos ^{-1} \frac{3}{5}+\cos ^{-1} \frac{12}{13}\right)\)
Solution:

(ii) \(\tan \left(\sin ^{-1} \frac{3}{5}+\cos ^{-1} \frac{5}{\sqrt{34}}\right)\)
Solution:

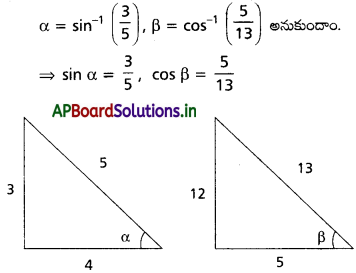
(iii) \(\cos \left(\sin ^{-1} \frac{3}{5}+\sin ^{-1} \frac{5}{13}\right)\)
Solution:

Question 3.
కింది వాటిని రుజువు చేయండి.
(i) \(\cos \left[2 \tan ^{-1} \frac{1}{7}\right]=\sin \left[2 \tan ^{-1} \frac{3}{4}\right]\)
Solution:
\(\tan ^{-1} \frac{1}{7}\) = α
⇒ tan α = \(\frac{1}{7}\)

(ii) \(\tan \left[2 \tan ^{-1} \cdot\left(\frac{\sqrt{5}-1}{2}\right)\right]=2\)
Solution:

(iii) \(\cos \left\{2\left[\tan ^{-1}\left(\frac{1}{4}\right)+\tan ^{-1}\left(\frac{2}{9}\right)\right]\right\}=\frac{3}{5}\)
Solution:

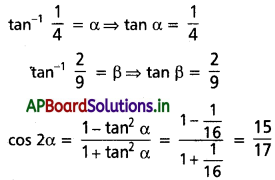
Question 4.
కింది వాటిని రుజువు చేయండి.
(i) \(\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{13}-\tan ^{-1} \frac{2}{9}=0\)
Solution:

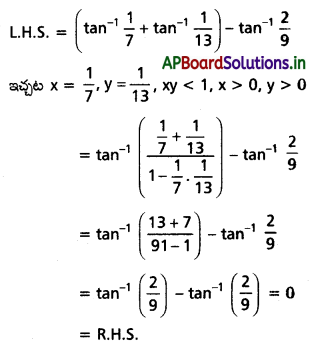
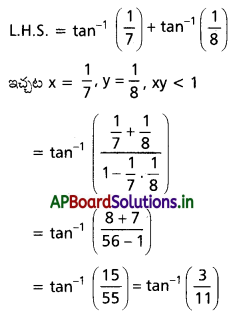
(ii) \(\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}\) [(A.P) Mar. ’15, ’11; May ’06]
Solution:

(iii) \(\tan ^{-1} \frac{3}{4}+\tan ^{-1} \frac{3}{5}-\tan ^{-1} \frac{8}{19}=\frac{\pi}{4}\)
Solution:

(iv) \(\tan ^{-1}\left(\frac{1}{7}\right)+\tan ^{-1}\left(\frac{1}{8}\right)\) = \(\cot ^{-1}\left(\frac{201}{43}\right)+\cot ^{-1}(18)\)
Solution:

Question 5.
(i) sec²(tan^-1 2) + cosec²(cot^-1 2) = 10 అని చూపండి.
Solution:
Let α = tan^-1 2 ⇒ tan α = 2
sec²α = 1 + tan²α = 1 + 4 = 5
Let β = cot^-1 2 ⇒ cot β = 2
cosec²β = 1 + cot²β = 1 + 4 = 5
L.H.S. = sec²(tan^-1 2) + cosec² (cot^-1 2)
= 5 + 5
= 10
= R.H.S.

(ii) \(\tan \left(\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}\right)\) విలువను కనుక్కోండి.
Solution:

(iii) sin^-1 x – cos^-1 x = \(\frac{\pi}{6}\) అయితే x విలువను కనుక్కోండి.
Solution:

III.

Question 1.
క్రింది వాటిని రుజువు చేయండి.
(i) \(2 \sin ^{-1}\left(\frac{3}{5}\right)-\cos ^{-1}\left(\frac{5}{13}\right)=\cos ^{-1}\left(\frac{323}{325}\right)\) [Mar. ’14]
Solution:

(ii) \(\sin ^{-1} \frac{4}{5}+2 \tan ^{-1} \frac{1}{3}=\frac{\pi}{2}\) [(T.S) Mar. ’15]
Solution:

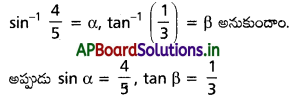
(iii) \(4 \tan ^{-1}\left(\frac{1}{5}\right)+\tan ^{-1} \frac{1}{99}-\tan ^{-1} \frac{1}{70}=\frac{\pi}{4}\)
Solution:

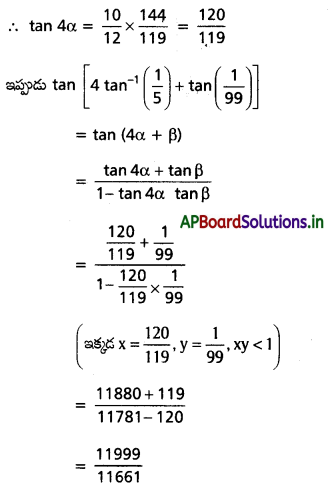
Question 2.
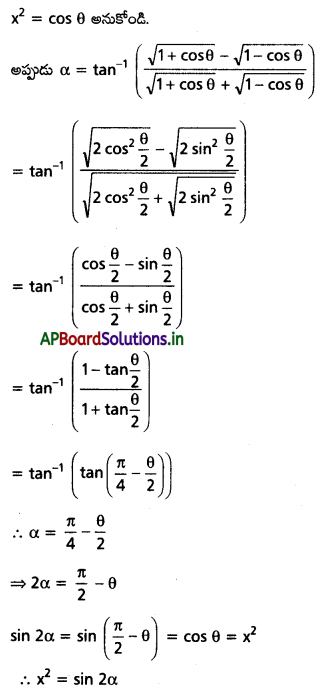
(i) α = \(\tan ^{-1}\left(\frac{\sqrt{1+x^2}-\sqrt{1-x^2}}{\sqrt{1+x^2}+\sqrt{1-x^2}}\right)\), అయితే x² = sin 2α అని చూపండి.
Solution:

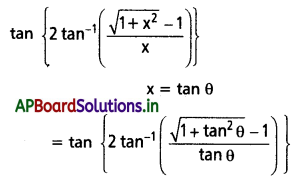
(ii) \(\tan \left\{2-\tan ^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)\right\}\) = x అని చూపండి.
Solution:

(iii) \(\sin \left[\cot ^{-1} \frac{2 x}{1-x^2}+\cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\right]\) = 1 అని చూపండి.
Solution:

(iv) \(\tan \left(\frac{\pi}{4}+\frac{1}{2} \cos ^{-1} \frac{a}{b}\right)+\tan \left(\frac{\pi}{4}-\frac{1}{2} \cos ^{-1} \frac{a}{b}\right)\) = \(\frac{2 b}{a}\) అని చూపండి.
Solution:

Question 3.
(i) cos^-1 p + cos^-1 q + cos^-1 r = π అయితే p² + q² + r² + 2pqr = 1 అని చూపండి. [June ’04]
Solution:
cos^-1 p = A, cos^-1 q = B, cos^-1 r = C అయితే
A + B + C = π అవుతుంది …….(1)
⇒ p = cos A, q = cos B, r = cos C
ఇప్పుడు p² + q² + r² = cos²A + cos²B + cos²C
= cos²A + (1 – sin²B) + cos²C
= 1 + (cos²A – sin²B + cos²C)
= 1 + cos(A + B) . cos (A – B) + cos²C
= 1+ cos(π – C) cos(A – B) + cos²C ((1) నుంచి)
= 1 – cos C cos(A – B) + cos²C
= 1 – cos C [cos(A – B) – cos C]
= 1 – cos C [cos(A – B) – cos (180° – \(\overline{A+B}\)]
= 1 – cos C [cos(A – B) + cos(A + B)]
= 1 – cos C [2 cos A cos B]
= 1 – 2pqr
∴ p² + q² + r² + 2pqr = 1

(ii) \(\sin ^{-1}\left[\frac{2 p}{1+p^2}\right]-\cos ^{-1}\left(\frac{1-q^2}{1+q^2}\right)\) = \(\tan ^{-1}\left[\frac{2 x}{1-x^2}\right]\), అయితే x = \(\frac{p-q}{1+p q}\) అని చూపండి.
Solution:

(iii) a, b, c లు ఒకే గుర్తు గల విభిన్న శూన్యేతర వాస్తవ సంఖ్యలు అయితే \(\cot ^{-1}\left(\frac{a b+1}{a-b}\right)+\cot ^{-1}\left(\frac{b c+1}{b-c}\right)\) + \(\cot ^{-1}\left(\frac{c a+1}{c-a}\right)\) = π లేదా 2π అని చూపండి.
Solution:
∵ (a – b) + (b – c) + (c – a) = 0
(a – b), (b – c), (c – a) లన్నింటికీ ఒకే గుర్తు ఉండదు. రెండు సందర్భాలు వస్తాయి. పై మూడింటిలో ఏవేని రెండు ధనాత్మకాలు, ఒకటి ఋణాత్మకం, లేదా రెండు ఋణాత్మకాలు, ఒకటి ధనాత్మకం.
సందర్భం (i): (a – b), (b – c) లు ధనాత్మకాలు, (c – a) ఋణాత్మకం అనుకోండి.

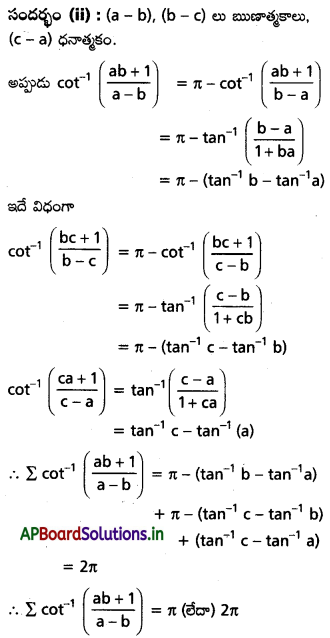
(iv) sin^-1 x + sin^-1 y + sin^-1 z = π అయితే \(x \sqrt{1-x^2}+y \sqrt{1-y^2}+z \sqrt{1-z^2}\) = 2xyz అని చూపండి. [Mar. ’06; May ’05]
Solution:
sin^-1(x) = A, sin^-1(y) = B, sin^-1(z) = C అయిన
A + B + C = π ……(1)
x = sin A, y = sin B, z = sin C
L.H.S. = \(x \sqrt{1-x^2}+y \sqrt{1-y^2}+z \sqrt{1-z^2}\)
= sin A \(\sqrt{1-\sin ^2 A}\) + sin B \(\sqrt{1-\sin ^2 B}\) + sin C \(\sqrt{1-\sin ^2 C}\)
= sin A cos A + sin B cos B + sin C cos C
= \(\frac{1}{2}\) [sin 2A + sin 2B + sin 2C]
= \(\frac{1}{2}\) [2 . sin(A + B) cos(A – B) + sin 2C]
= \(\frac{1}{2}\) [2 sin(π – c). cos (A – B) + sin 2C]
= \(\frac{1}{2}\) [2 sin C cos (A – B) + 2 sin C cos C]
= \(\frac{1}{2}\) (2 sin C) [cos (A – B) + cos C]
= sin C [cos(A – B) + cos (180° – \(\overline{A+B}\)]
= sin C [cos(A – B) – cos(A + B)]
= sin C [2 sin A sin B]
= 2xyz
∴ x \sqrt{1-x^2}+y \sqrt{1-y^2}+z \sqrt{1-z^2} = 2xyz

(v) (a) tan^-1 x + tan^-1 y + tan^-1 z = π, అయితే x + y + z = xyz
Solution:
A = tan^-1 x, B = tan^-1 y, C = tan^-1 z
⇒ tan A = x, tan B = y, tan C = z
A + B + C = π ……….(1)
A + B = π – C
tan(A + B) = tan(π – C)
\(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = -tan C
\(\frac{x+y}{1-x y}\) = -z
x + y = -z + xyz
∴ x + y + z = xyz

(b) tan^-1 x + tan^-1 y + tan^-1 z = \(\frac{\pi}{2}\) అయితే, xy + yz + zx = 1
Solution:

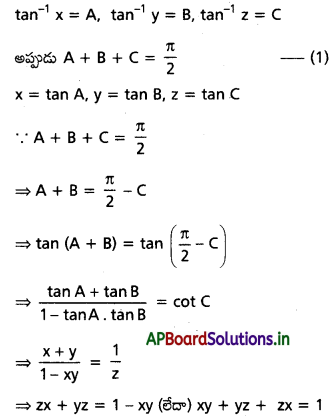
Question 4.
క్రింది సమీకరణాలను సాధించండి.
(i) \({tan}^{-1}\left(\frac{x-1}{x-2}\right)+{tan}^{-1}\left(\frac{x+1}{x+2}\right)=\frac{\pi}{4}\)
Solution:

(ii) \(\tan ^{-1}\left(\frac{1}{2 x+1}\right)+\tan ^{-1}\left(\frac{1}{4 x+1}\right)\) = \(\tan ^{-1}\left(\frac{2}{x^2}\right)\)
Solution:

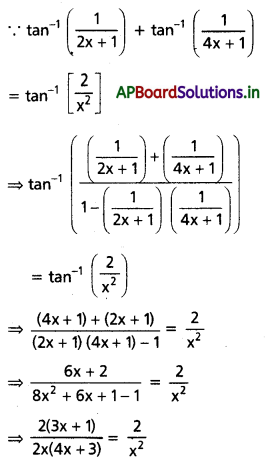
x² (3x + 1) = 2x (4x + 3)
x[x(3x + 1) – 2(4x + 3)] = 0
⇒ x = 0 (లేదా) 3x² – 7x – 6 = 0
⇒ x = 0 (లేదా) 3x² – 9x + 2x – 6 = 0
⇒ x = 0 (లేదా) 3x(x – 3) + 2(x – 3) = 0
⇒ x = 0 (లేదా) (3x + 2) (x – 3) = 0
⇒ x = 0 (లేదా) 3 (లేదా) \(\frac{-2}{3}\)

(iii) \(3 \sin ^{-1}\left(\frac{2 x}{1+x^2}\right)-4 \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\) + \(2 \tan ^{-1}\left(\frac{2 x}{1-x^2}\right)=\frac{\pi}{3}\)
Solution:

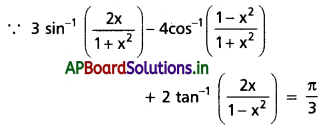
(iv) sin^-1(1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\)
Solution:
sin^-1(1 – x) – 2 sin^-1x = \(\frac{\pi}{2}\)
sin^-1(1 – x) = α, sin^-1(x) = β అనుకుంటే
sin α = (1 – x), sin β = x
cos α = \(\sqrt{1-(1-x)^2}\), cos β = \(\sqrt{1-x^2}\)
ఇప్పుడు sin^-1(1 – x) – 2 sin^-1(x) = \(\frac{\pi}{2}\)
α – 2β = \(\frac{\pi}{2}\)
α = \(\frac{\pi}{2}\) + 2β
⇒ sin α = sin[\(\frac{\pi}{2}\) + 2β]
⇒ sin α = cos 2β
⇒ 1 – x = 1 – 2 sin²β
⇒ 1 – x = 1 – 2x²
⇒ 2x² – x = 0
⇒ x(2x – 1) = 0
⇒ x = 0 (లేదా) x = \(\frac{1}{2}\)
కాని x = \(\frac{1}{2}\) అయినప్పుడు

కాబట్టి x = 0 ఒకటి మాత్రమే దత్త సమీకరణానికి సాధన.

Question 5.
కింది సమీకరణాలను సాధించండి.
(i) \(\cot ^{-1}\left(\frac{1+x}{1-x}\right)=\frac{1}{2} \cot ^{-1}\left(\frac{1}{x}\right)\), x > 0, x ≠ 1
Solution:

x = \(\frac{-1}{\sqrt{3}}\) కాబట్టి ఇచ్చిన సమీకరణాన్ని సంతృప్తి పర్చలేదు.
∴ x = \(\frac{-1}{\sqrt{3}}\)

(ii) \(\tan \left[\cos ^{-1} \frac{1}{x}\right]=\sin \left[\cot ^{-1} \frac{1}{2}\right]\); x ≠ 0
Solution:

(iii) \(\cos ^{-1} x+\sin ^{-1} \frac{x}{2}=\frac{\pi}{6}\)
Solution:

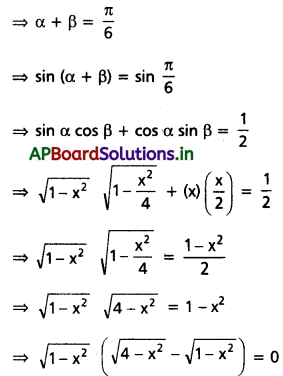
(iv) cos^-1(√3 . x) + cos^-1x = \(\frac{\pi}{2}\)
Solution:
α = cos^-1(√3x)
⇒ cos α = √3x అనుకుందాం.
β = cos^-1x
⇒ cos β = x
cos (α + β) = cos \(\frac{\pi}{2}\)
cos α cos β – sin α sin β = 0
⇒ \((\sqrt{3 x}) x-\left(\sqrt{1-3 x^2}\right)\left(\sqrt{1-x^2}\right)=0\)
⇒ \(\sqrt{3 x^2}=\sqrt{\left(1-3 x^2\right)\left(1-x^2\right)}\)
ఇరువైపులా వర్గం చేయగా
⇒ 3x⁴ = 1 – x² – 3x² + 3x⁴
⇒ 0 = 1 – 4x²
⇒ 4x² = 1
⇒ x = \(\frac{1}{2}\)

(v) \(\sin \left[\sin ^{-1}\left(\frac{1}{5}\right)+\cos ^{-1} x\right]=1\)
Solution: