AP Inter 1st Year Maths 1A Solutions Chapter 10 త్రిభుజ ధర్మాలు Ex 10(b)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 10 త్రిభుజ ధర్మాలు Exercise 10(b) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 10 త్రిభుజ ధర్మాలు Exercise 10(b)

I. ఈ అభ్యాసం లోని అన్ని సమస్యలు ∆ABC కి సంబంధించినవి.

Question 1.
Σ r₁ cot \(\frac{A}{2}\) ని s పదాలలో వ్యక్తపరచండి. [May ’11]
Solution:
Σ r₁ cot \(\frac{A}{2}\)
= Σ (s tan \(\frac{A}{2}\)) cot \(\frac{A}{2}\)
= Σ s
= s + s + s
= 3s

Question 2.
Σ a cot A = 2(R + r) అని చూపండి.
Solution:

Question 3.
r₁ + r₂ + r₃ – r = 4R అని నిరూపించండి. [Mar. ’06]
Solution:

Question 4.
r + r₁ + r₂ – r₃ = 4R cos C అని నిరూపించండి. [May ’06]
Solution:

Question 5.
r₁ + r₂ = r₃ – r అయితే, C = 90° అని చూపండి.
Solution:

II.

Question 1.
4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)² అని నిరూపించండి.
Solution:

Question 2.
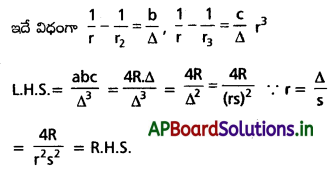
\(\left(\frac{1}{r}-\frac{1}{r_1}\right)\left(\frac{1}{r}-\frac{1}{r_2}\right)\left(\frac{1}{r}-\frac{1}{r_3}\right)=\frac{a b c}{\Delta^3}=\frac{4 R}{r^2 s^2}\) అని నిరూపించండి.
Solution:

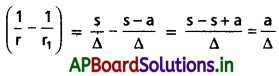
Question 3.
r(r₁ + r₂ + r₃) = ab + bc + ca – s² అని నిరూపించండి.
Solution:

Question 4.
\(\sum \frac{r_1}{(s-b)(s-c)}=\frac{3}{r}\) అని చూపండి.
Solution:

Question 5.
(r₁ + r₂) tan \(\frac{C}{2}\) = (r₃ – r) cot \(\frac{C}{2}\) = c అని చూపండి.
Solution:

Question 6.
r₁r₂r₃ = \(r^3 \cot ^2 \frac{A}{2} \cdot \cot ^2 \frac{B}{2} \cdot \cot ^2 \frac{C}{2}\) అని చూపండి.
Solution:

III.

Question 1.
cos A + cos B + cos C = 1 + \(\frac{r}{R}\) అని చూపండి.
Solution:
L.H.S. = cos A + cos B + cos C

Question 2.
\(\cos ^2 \frac{A}{2}+\cos ^2 \frac{B}{2}+\cos ^2 \frac{C}{2}=2+\frac{r}{2 R}\) అని చూపండి. [Mar. ’05]
Solution:

Question 3.
\(\sin ^2 \frac{A}{2}+\sin ^2 \frac{B}{2}+\sin ^2 \frac{C}{2}=1-\frac{r}{2 R}\) అని చూపండి.
Solution:

Question 4.
(i) a = (r₂ + r₃) \(\sqrt{\frac{r r_1}{r_2 r_3}}\)
(ii) ∆ = r₁r₂ \(\sqrt{\frac{4 R-r_1-r_2}{r_1+r_2}}\) అని చూపండి.
Solution:

Question 5.
\(r_1^2+r_2^2+r_3^2+r^2\) = 16R² – (a² + b² + c²) అని నిరూపించండి.
Solution:

= 2(3s² – 2s(2s) + (ab + bc + ca))
= 2(3s² – 4s² + (ab + bc + ca))
= -2s² + 2(ab + bc + ca) ………(3)
(2) నుంచి \(r_1^2+r_2^2+r_3^2+r^2\)
= 16R² – 2s² + 2(ab + bc + ca) – 2s²
= 16R² – (4s² – 2(ab + bc + ca))
= 16R² – ((a + b + c)² – 2(ab + bc + ca))
= 16R² – (a² + b² + c²)

Question 6.
A, B, C శీర్షాల నుంచి ఎదుటి భుజాలకు గీసిన ఉన్నతులు P₁, P₂, P₃ అయితే,
(i) \(\frac{1}{p_1}+\frac{1}{p_2}+\frac{1}{p_3}=\frac{1}{r}\)
(ii) \(\frac{1}{p_1}+\frac{1}{p_2}-\frac{1}{p_3}=\frac{1}{r_3}\)
(iii) p₁ . p₂ . p₃ = \(\frac{(a b c)^2}{8 R^3}=\frac{8 \Delta^3}{a b c}\) అని చూపండి.
Solution:

Question 7.
a = 13, b = 14, c = 15 అయితే, R = \(\frac{65}{8}\), r = 4, r₁ = \(\frac{21}{2}\), r₂ = 12, r₃ = 14 అని చూపండి. [(A.P) Mar. ’15, ’14; May ’11]
Solution:

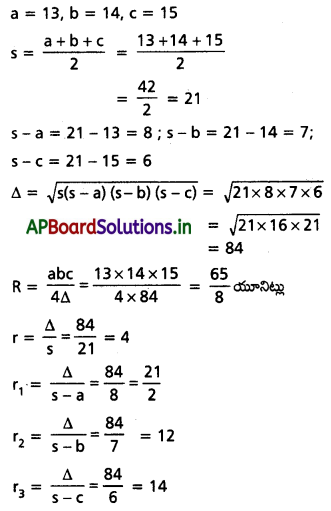
Question 8.
r₁ = 2, r₂ = 3, r₃ = 6, r = 1 అయితే, a = 3, b = 4, c = 5 అని చూపండి. [(T.S) Mar. ’15]
Solution: