Students get through AP Inter 1st Year Maths 1B Important Questions Chapter 7 సమతలం which are most likely to be asked in the exam.
AP Inter 1st Year Maths 1B Important Questions Chapter 7 సమతలం
సాధించిన సమస్యలు
ప్రశ్న 1.
మూలబిందువు నుంచి తలానికి లంబపాదం A(2, 3, -5) అయితే ఆ తలం సమీకరణం కనుక్కోండి.
సాధన:
0 (0, 0, 0), A (2, 3, -5) లు దత్త బిందువులు.
OA యొక్క D.R.లు 2, 3, -5
OA సమతలానికి లంబంగా ఉంది. ఇది A (2, 3, -5) గుండా పోతుంది.
సమతల సమీకరణం
2(x -2) + 3(y – 3) – 5 (z – 5) = 0
2x – 4 + 3y – 9 – 5z – 25 = 0
2x + 3y – 5z – 38 = 0
![]()
ప్రశ్న 2.
(0, -1, -1) (4, 5, 1), (3, 9, 4) బిందువుల గుండా పోయే తలం సమీకరణం కనుక్కోండి.
సాధన:
A(0, -1, -1), B(4, 5, 1), ((3, 9, 4) లు దత్త బిందువులు.
పోయే సమతల సమీకరణము
a(x – 0) + b(y + 1) + c(z + 1) = 0 ………………. (1)
B(4, 5, 1), C(3, 9, 4) ల గుండా పోతుంది.
4a + 6b + 2c = 0 …………….. (2)
3a + 10b + 5c = 0 ……………… (3)
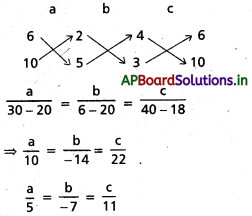
(1) లో ప్రతిక్షేపించగా, ABC తల సమీకరణము
5x – 7 (y + 1) + 11 (z + 1) = 0
5x – 7y – 7 + 11z + 11 = 0
5x – 7y + 11z + 4 = 0
ప్రశ్న 3.
ZX- తలానికి సమాంతరంగా ఉండి (0, 4, 4) బిందువు. గుండా పోయే తలం సమీకరణం కనుక్కోండి.
సాధన:
ZX తల సమీకరణము y = 0
సమాంతర సమతల సమీకరణము y = k
ఈ తలం P(0, 4, 4) = 4 = k గుండా పోతుంది.
కావలసిన సమతల సమీకరణము y = 4.
![]()
ప్రశ్న 4.
(α, β, γ) బిందువు గుండా పోతూ ax + by + cz = 0 తలానికి సమాంతరంగా ఉండే తలం సమీకరణం రాబట్టండి.
సాధన:
దత్త సమతల సమీకరణము ax + by + cz = 0
సమాంతర సమతల సమీకరణము ax + by + cz = K
ఈ తలం P(α, β, γ) గుండా పోతుంది.
aα + bβ + cγ = K
∴ కావలసిన సమతల సమీకరణము
ax + by + cz = aα + bβ + cγ
i.e., a(x – α) + b(y – β) + c(z – γ) = 0.
ప్రశ్న 5.
2x – y + z = 6, x + 2y + 2z = 75 సూచించే తలాల మధ్యకోణం కనుక్కోండి. [A.P Mar. ’15, ’11]
సాధన:
సమతలాల సమీకరణము
2x – y + z = 6; x + y + 2z = 7
సమతలాల మధ్యకోణము θ అయితే
cos θ = \(\frac{\left|a_1 a_2+b_1 b_2+c_1 c_2\right|}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\)
= \(\frac{|2.1+(-1) \cdot 1+1.2|}{\sqrt{4+1+1} \sqrt{1+1+4}}\)
= \(\frac{3}{6}=\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
∴ θ = \(\frac{\pi}{2}\)
![]()
ప్రశ్న 6.
(2, 0, 1), (3, -3, 4) బిందువుల గుండాపోతూ, x – 2y + 2 = 6 తలానికి లంబంగా ఉండే తలం సమీకరణం కనుక్కోండి.
సాధన:
(2, 0, 1) గుండా పోయే సమతల సమీకరణము
a(x – 2) + by + c(z – 1) = 0 ……………… (1)
ఈ తలం B(3, -3, 4) గుండా పోతుంది.
a – 3b + 3c = 0 …………………. (2)
(1)వ తలము x – 2y + 2 = 6 కు లంబముగా ఉంది.
a – 2b + c = 0 ……………… (3)
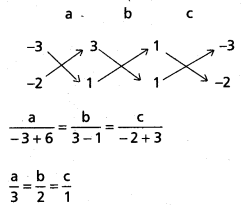
(1) లో ప్రతిక్షేపిస్తే, కావలసిన సమతల సమీకరణము
3(x – 2)+ 2y +1 (z – 1) = 0
3x – 6 + 2y + z – 1 = 0
3x + 2y + z – 7 = 0
3x + 2y + z = 7
![]()
ప్రశ్న 7.
సమతల సమీకరణం x + 2y – 2z – 9 = 0 అని అభిలంబ రూపానికి కుదించి అభిలంబ రేఖ దిక్ కొసైన్లను మూల బిందువు నుంచి సమతలానికి దూరాన్ని కనుక్కోండి.
సాధన:
దత్త సమతల సమీకరణం x + 2y – 2z – 9 = 0
స్థిర రాశిని కుడివైపు రాస్తే,
x + 2y – 2z = 9 ……………… (1)
(1) లో x, y, z ల గుణకాల వర్గాల మొత్తానికి వర్గమూలం
\(\sqrt{1^2+2^2+2^2}\) = ±3
p = ±\(\left(\frac{-9}{\pm 3}\right)\) = 3
(1) ని ± 3 తో భాగిస్తే
± \(\frac{1}{3}\)x ± \(\frac{2}{3}\)y ± \(\frac{2}{3}\)z = ±3
కుడివైపు స్థిరరాశి గుర్తు ధనాత్మకం అయ్యేలా సమీకరణం అభిలంబ రూపంలో తలం సమీకరణం గుర్తు ఎంచుకొంటే,
\(\frac{x}{3}\) + \(\frac{2}{3}\)y – \(\frac{2}{3}\)z = 3 …………………. (2)
(2) నుంచి అభిలంబ రేఖ దిక్ కొసైన్లు (\(\frac{1}{3}\), \(\frac{2}{3}\), –\(\frac{2}{3}\))
మూలబిందువు నుంచి తలానికి లంబదూరం = 3 యూనిట్లు
ప్రశ్న 8.
ఒక సమతలం X, Y, Z – అక్షాలపై చేసే అంతర ఖండాలు వరుసగా 2,3,4 అయితే, a, b, c లు వరుసగా X, Y, Z – అంతర ఖండాలుగా గల సమతల సమీకరణం \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) అని చూపండి.
సాధన:
సమతల సమీకరణం
\(\frac{x}{2}+\frac{y}{3}+\frac{z}{4}\) = 1 నుంచి
లేదా 6x + 4y + 3z = 12
![]()
ప్రశ్న 9.
x – 3y + 2z = 9 సమతలం గల సమీకరణం కనుక్కోండి.
సాధన:
x – 3y + 2z = 9 ను 9 తో భాగిస్తే
\(\frac{x}{9}+\frac{y}{-3}+\frac{9}{9 / 2}\) = 1
దీనిని \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1 తో పోలిస్తే,
X-అంతరఖండం = a = 9,
Y-అంతరఖండం = b = -3,
Z-అంతరఖండం = c = \(\frac{9}{2}\)