AP Inter 1st Year Maths 1B Important Questions Chapter 9 అవకలనం

Students get through AP Inter 1st Year Maths 1B Important Questions Chapter 9 అవకలనం which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1B Important Questions Chapter 9 అవకలనం

సాధించిన సమస్యలు

ప్రశ్న 1.
f(x) = x² (x ∈ R), అయితే R పై f అవకలనీయమని చూపి దాని అవకలజాన్ని కనుక్కోండి.
సాధన:
f(x) = x² అనుకుందాం.

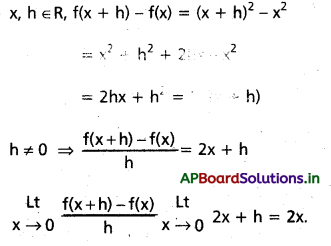
∴ f ప్రమేయము R మీద అవకలనీయము
f'(x) = 2x ∀ x ∈ R

ప్రశ్న 2.
f(x) = \(\sqrt{x}\) (x > 0). (0, ∞) పై f అవకలనీయం అని నిరూపించి P(x) ను కనుక్కోండి.
సాధన:
x ∈ (0, ∞)h ≠ 0 మరియు |h| < 0

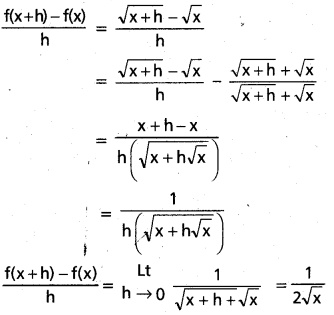
f ప్రమేయము (0, ∞) మీద అవకలనీయము f'(x) \(\frac{1}{2 \sqrt{x}}\)

ప్రశ్న3.
f(x) = \(\frac{1}{x^2+1}\) (x ∈ R) అయితే R పై f అవకలనీయం అని నిరూపించి f'(x) కనుక్కోండి.
సాధన:
x ∈ R మరియు h ≠ 0 అనుకుందాం.

∴ f అవకలనీయము మరియు f'(x) = \(\frac{2 x}{\left(x^2+1\right)^2}\), ∀ x ∈ R

ప్రశ్న 4.
f(x) = sin x (x ∈ R) అయితే R పై f అవకలనీయం, f'(x) = cos x అని చూపండి.
సాధన:
x ∈ R మరియు h ≠ 0 అనుకుందాం.

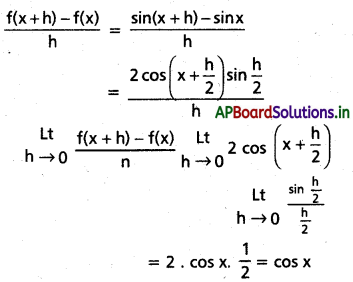
∴ f ప్రమేయం R మరియు అవకలనీయము f'(x) = cos x వద్ద ∀ x ∈ R

ప్రశ్న 5.
f(x) = |x| (x ∈ R) ప్రమేయం సున్నా వద్ద అవకలనీయం కాదని, ప్రతి x ≠ 0 వద్ద f అవకలనీయమని చూపండి.
సాధన:

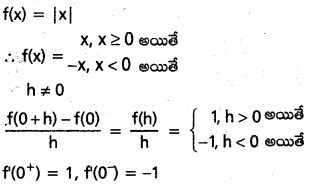
∴ 0 వద్ద f అవకలనీయము కాదు.
x ≠ 0 అయితే f అవకలనీయమని మరియు

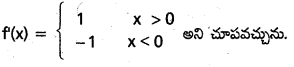
ప్రశ్న 6.
క్రింద పేర్కొన్న ప్రమేయం సున్నా వద్ద అవకలనీయమేమో చూడండి.

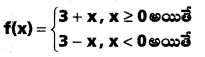
సాధన:


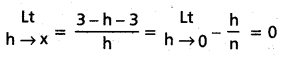
f యొక్క ఎడమ అవకలజము -1, f'(0^–) = -1
∴ f'(0⁺) ≠ f(0^–)
f(x) ప్రమేయము 0 వద్ద అవకలనీయం కాదు.

ప్రశ్న 7.
ఒక అంతరంపై ఏదైనా స్థిర ప్రమేయం అవకలజం సున్నా అని చూపండి.
సాధన:
ప్రమేయము I అంతరంలోని f.
f(x) = C ∀ x ∈ I, c స్థిరము.

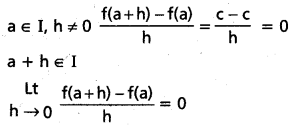
∴ f, 0 వద్ద అవకలనీయము f'(a) = 0

ప్రశ్న 8.
అన్ని x, y ∈ R లకు f(x + y) = f(x). f(y) అని f'(0) వ్యవస్థితమని అనుకోండి. అప్పుడు ప్రతీ x ∈ R కు f(x) వ్యవస్థితమని అది f(x). f'(0) కు సమానమని చూపండి.
సాధన:
x ∈ R, h ≠ 0,
\(\frac{f(x+h)-f(x)}{h}\) = \(\frac{f(x) f(h)-f(x)}{h}\)
= \(f(x) \frac{[f(h)-1]}{h}\) —– (1)
f(0) = f(0 + 0) = f(0) f(0)
⇒ (0) (1 − f(0))
∴ f(0) = 0, f(0) = 1
సందర్భం i) : f(0) = 0 అయితే
f(x) = f(x + 0) = f(x) f(0) = 0 ∀ x ∈ R
∴ f(x) స్థిర ప్రమేయము ⇒ f'(x) = 0
∀ x ∈ R
∴ f'(x) = 0 = f(x).f'(0)
సందర్భం ii) : f(0) = 1 అయితే

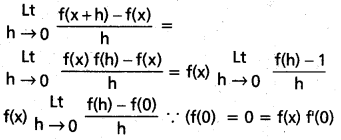
∴ f అవకలనీయం మరియు f”(x) = f(x) f'(0).

ప్రశ్న 9.
f(x) = (ax + b)ⁿ (x > \(-\frac{\mathbf{b}}{\mathbf{a}}\)), అయితే f'(x) కనుక్కోండి.
సాధన:
ս = ax + by ⇒ y = uⁿ
f'(x) = \(\frac{d}{d n}\left(u^n\right) \frac{d u}{d x}\)
= n. u^n-1a
= an (ax + b)^n-1

ప్రశ్న 10.
f(x) = e^x (x² + 1) యొక్క అవకలజాన్ని కనుక్కోండి.
సాధన:
u = e^x = x² + 1
\(\frac{d u}{d x}\) = e^x, \(\frac{d v}{d x}\) = 2x
f(x) = u(x). v(x)
f'(x) = u(x). v'(x) + u'(x) . v(x)
= e^x. 2x + (x² + 1) e^x
= e^x (2x + x² + 1)
= e^x (x + 1)²

ప్రశ్న 11.
y = \(\frac{a-\mathbf{x}}{\mathbf{a}+\mathbf{x}}\) (x ≠ -a) అయితే \(\frac{d y}{d x}\) కనుక్కోండి.
సాధన:
u = a – x మరియు u = a + x అయితే y = \(\frac{u}{v}\)

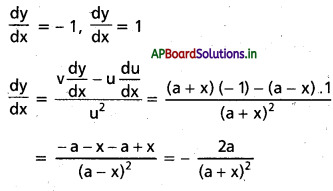
ప్రశ్న 12.
f(x) = e^2x.log x (x > 0) అయితే f'(x) కనుక్కోండి.
సాధన:
u = e^2x, v = log x అయితే,
\(\frac{\mathrm{du}}{\mathrm{dx}}\) = 2.e^2x, \(\frac{d v}{d x}\) = \(\frac{1}{x}\)
f(x) = u.v
f'(x) = u. \(\frac{d v}{d x}\) + v. \(\frac{\mathrm{du}}{\mathrm{dx}}\)
= e^2x. \(\frac{1}{x}\) + log x (2e^2x)
= e^2x(\(\frac{1}{x}\) + 2logx)

ప్రశ్న 13.
f(x) = \(\sqrt{\frac{1+x^2}{1-x^2}}\) (|x| < 1) అయితే f'(x) ను కనుక్కోండి
సాధన:

ప్రశ్న 14.
f(x) = x² . 2^x log x(x > 0) అయితే f'(x) ను కనుక్కోండి.
సాధన:

ప్రశ్న 15.

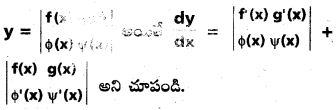
సాధన:

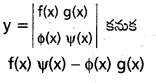
ప్రశ్న 16.
f(x) = 7^{x3 +3x} (x > 0) అయితే f'(x) ను కనుక్కోండి.
సాధన:
u = x³ + 3x ⇒ \(\frac{\mathrm{du}}{\mathrm{dx}}\) = 3x² + 3 = 3 (x² + 1)
f(x) = 7^u ⇒ f'(x) = 7^u log 7
f'(x) = \(\frac{d f}{d u} \cdot \frac{d u}{d x}\) = (7^u. log 7) [3(x² + 1)]
= 3(x² + 1) 7^{x3 + 3x} log 7

ప్రశ్న 17.
f(x) = x e^x అయితే f'(x) ను కనుక్కోండి.
సాధన:
u = x, v = e^x, w = sin x అనుకుందాం
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 1, \(\frac{\mathrm{dv}}{\mathrm{dx}}\) = e^x. \(\frac{d w}{d x}\) = cos x
f(x) = u.v.w
f”(x) = uv. \(\frac{d w}{d x}\) + uw \(\frac{d v}{d x}\) + vw \(\frac{d u}{d x}\)
= xe^x cos x + x. sinx . e^x + e^x sin x

ప్రశ్న 18.
f(x) sin (log x) (x > 0) అయితే f'(x) ను కనుక్కోండి.
సాధన:
u = log x, y = f(x) ⇒ y = sin u
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{d y}{d u} \cdot \frac{d u}{d x}\)
\(\frac{\mathrm{dy}}{\mathrm{du}}\) = cos u, \(\frac{\mathrm{du}}{\mathrm{dx}}\) = \(\frac{1}{x}\)
f'(x) = \(\frac{1}{x}\). cos u = \(\frac{1}{x}\) cos (log x)

ప్రశ్న 19.
f(x) = (x³ + 6x² + 12x – 13) అయితే f'(x) కనుక్కోండి.
సాధన:
u = x³ + 6x² + 12x – 13
⇒ \(\frac{\mathrm{du}}{\mathrm{dx}}\) = 3x² + 12x + 12
= 3(x² + 4x + 4)
= 3(x + 2)²
f(x) = u¹⁰⁰
f(x) = 100.u⁹⁹. \(\frac{\mathrm{du}}{\mathrm{dv}}\)
= 100(x³ + 6x² + 12x – 13)⁹⁹. 3(x + 2)²
= 300 (x + 2)² (x³ + 6x² + 12x – 13)⁹⁹

ప్రశ్న 20.
f(x) = \(\frac{x \cos x}{\sqrt{1+x^2}}\) యొక్క అవకలజం కనుక్కోండి.
సాధన:

ప్రశ్న 21.
f(x) = log (sec x + tan x) అయితే f'(x) కనుకోండి. (Mar. ’14, May ’11)
సాధన:
u = sec x + tan x, y = log u
\(\frac{d y}{d u}\) = \(\frac{1}{u}\), \(\frac{\mathrm{du}}{\mathrm{dx}}\) = sec x. tan x + sec²x
= sec x (sec x + tan x)
\(\frac{d y}{d x}\) = \(\frac{\mathrm{dy}}{\mathrm{du}} \cdot \frac{\mathrm{du}}{\mathrm{dx}}\)
= \(\frac{1}{\sec x+\tan x}\). sec x (sec x + tan x) = sec x

ప్రశ్న 22.
y = sin^-1 \(\sqrt{\mathbf{x}}\) అయితే \(\frac{d y}{d x}\) కనుక్కోండి. (Mar. ’13)
సాధన:
u = \(\sqrt{x}\)
y = sin^-1 u.

ప్రశ్న 23.
y = sec \((\sqrt{\tan x})\) అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:

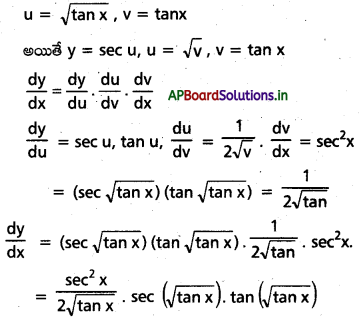
ప్రశ్న 24.
y = \((\sqrt{\tan x})\) అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:

ప్రశ్న 25.
y = log (cosh 2x) అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:
u = cosh 2x, అనుకుంటే y = log u
\(\frac{d y}{d x}\) = \(\frac{1}{u} \cdot \frac{d u}{d x}\) = 2 sin h2x
\(\frac{d y}{d x}\) = \(\frac{d y}{d u} \cdot \frac{d u}{d x}\)
= 2 sin h 2x. \(\frac{1}{\cosh 2 x}\) = 2 tan h 2x

ప్రశ్న 26.
y = log (sin(log x)) అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:

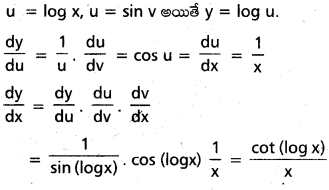
ప్రశ్న 27.
y = (cot^-1x³)² అయితే, \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:
u = cot^-1x³, u = x³, y = u²

ప్రశ్న 28.
y = cosec^-1(e^{2x + 1}) అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:

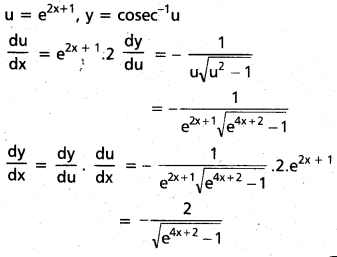
ప్రశ్న 29.
y = tan^-1 (cos \(\sqrt{\mathbf{x}}\)), అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:

ప్రశ్న 30.
y = tan^-1 \(\left(\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right)\), 0 < |x| < 1, అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:

ప్రశ్న 31.
y = x² e^x sin x అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:
log y = log x². e^x. sin x
= log x² + log e^x + log sin x
= 2 log x + e^x + log sin x
x దృష్ట్యా అవకలనం చేయగా
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = \(\frac{2}{x}\) + 1 + \(\frac{1}{\sin x}\) . cos x
\(\frac{d y}{d x}\) = y(\(\frac{2}{x}\) + 1 + cot x)

ప్రశ్న 32.
y = x^{tan x} + (sin x)^{cos x} అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి. (Mar. 14, ’11; May ’13)
సాధన:
u = x^{tan x}, v = (sin x)^{cos x}
log u = log x^{tan x} = (tan x) log x

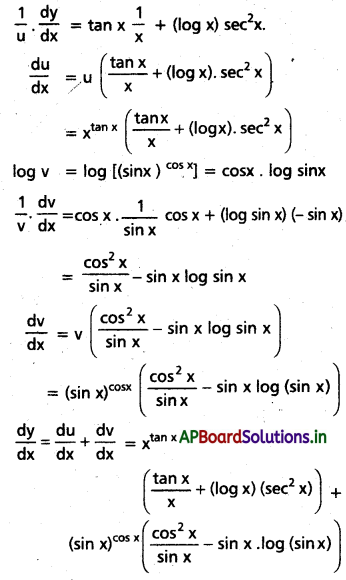
ప్రశ్న 33.
x = a(cos t + log tan\(\left(\frac{t}{2}\right)\)), y = a sin t, అయితే \(\frac{d y}{d x}\) ను కనుక్కోండి.
సాధన:

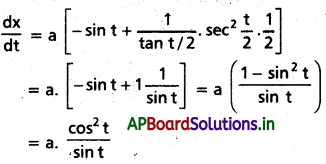
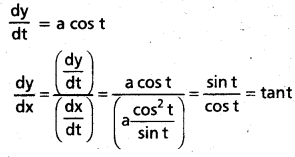
ప్రశ్న 34.
x^y = e^{x – y} అయితే \(\frac{d y}{d x}\) = \(\frac{\log x}{(1+\log x)^2}\) అని చూపండి.
సాధన:
x^y = e^{x – y}
log x^y = log e^{x – y}
y log x = x – y (log e = 1)
y(1 + log x) = x

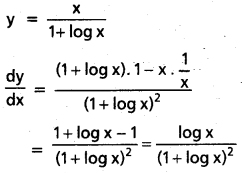
ప్రశ్న 35.
sin y = x sin (a + y) అయితే \(\frac{d y}{d x}\) = \(\frac{\sin ^2(a+y)}{\sin a}\) అని చూపండి.
(a అనేది π యొక్క గుణిజం కాదు)
సాధన:

ప్రశ్న 36.
y = x⁴ + tan x అయితే y” కనుక్కోండి.
సాధన:
y = x⁴ + tan x
\(\frac{d y}{d x}\) = 4x³ + sec² x
\(\frac{d^2 y}{d x^2}\) = 12x² + 2 sec²x. tan x

ప్రశ్న 37.
f(x) = sinx sin 2x sin 3x అయితే f”(x) ను కనుక్కోండి.
సాధన:
f(x) = \(\frac{1}{2}\)sin 2x (2 sin 3x sin x)
= \(\frac{1}{2}\)(sin 2x) (cos 2x – cos 4x)
= \(\frac{1}{4}\)(2 sin 2x cos 2x – 2 sin 2x cos 4x)
= \(\frac{1}{4}\)(sin 2x + sin 4x – sin 6x)
f'(x) = \(\frac{1}{4}\)[2 cos 2x + 4 cos 4x – 6 cos 6x]
f”(x) = \(\frac{1}{4}\)(-4 sin 2x – 16 sin 4x + 36 sin 6x)
= 9 sin 6x – 4 sin 4x – sin 2x.

ప్రశ్న 38.
cos²x \(\frac{d y^2}{d x^2}\) + 2x = 2y ని y = x + tan x తృప్తిపరుస్తుందని చూపండి.
సాధన:
y = x + tan x ⇒ y’ = 1 + sec² x
y’ cos² x = 1 + cos²x.
పై సమీకరణాన్ని ఇరువైపులా అవకలనం చేయగా
y” cos² x + y’.2 cos x (-sin x) = 2 cos x (- sin x)
∴ y” cos² x = 2(y’ – 1) sin x cos x
= 2 sec²x sin x cos x = 2 tan x = 2(y – x)
కావలసిన ఫలితము వచ్చినది.

ప్రశ్న 39.
x = a(t – sin t), y = a(1 + cos t) అయితే \(\frac{d^2 y}{d^2}\) ను కనుక్కోండి.
సాధన:

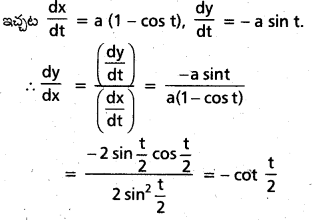
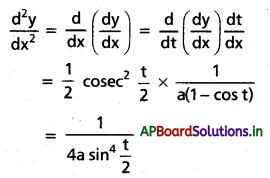
ప్రశ్న 40.
y = tan^-1 \(\left(\frac{2 x}{1-x^2}\right)\) కు రెండో పరిమాణం అవకలజాన్ని కనుక్కోండి.
సాధన:
x = tan θ అయితే
y = tan^-1 \(\left(\frac{2 \tan \theta}{1-\tan ^2 \theta}\right)\)
y = tan^-1(tan 2θ)
= 2θ = 2 tan^-1 x
∴ \(\frac{d y}{d x}\) = \(\frac{2}{1+x^2}\) and \(\frac{d^2 y}{d x^2}\) = \(\frac{-4 x}{\left(1+x^2\right)^2}\)

ప్రశ్న 41.
y = sin (sin x) అయితే
y” + (tan x) y’ + y cos² x = 0 అని చూపండి.
సాధన:
y = sin (sin x) అయితే
y’ = cos x. cos (sin x) మరియు
y” = – cos²x sin (sin x) – sin x cos (sin x)
= – y cos² x – sin x\(\left(\frac{y^{\prime}}{\cos x}\right)\)
= -y cos² x – y’ tan x
∴ y” + (tan x) y’ + y cos² x = 0.

ప్రశ్న 42.
f(x) = e^x(x∈R) అయితే ప్రాధమిక సూత్రాన్ని అనుసరించి f'(x) = e^x అని చూపండి.
సాధన:
h ≠ 0 కు f(x) = e^x నుంచి

ప్రశ్న 43.
f(x) = log x (x > 0) అయినప్పుడు ప్రాథమిక సూత్రాన్ని అనుసరించి f(x) = \(\frac{1}{x}\) అని చూపండి.
సాధన:

ప్రశ్న 44.
f(x) = x^x (x ∈ R) (a > 0) అయినప్పుడు ప్రాధమిక సూత్రాన్ని అనుసరించి f(x) = a^x అని చూపండి
సాధన:

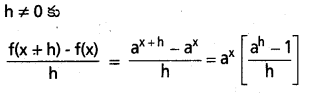
h→ 0 అయినప్పుడు \(\frac{a^h-1}{h}\) → log a అని మనకు తెలుసు. కాబట్టి f'(x) = a^x. log a.
\(\frac{d}{d x}\left(a^x\right)\) = a^x. log a

ప్రశ్న 45.
y = Tan^-1 \(\sqrt{\frac{1-x}{1+x}}(|x|<1)\) అయితే \(\frac{d y}{d x}\)ను కనుక్కోండి.
సాధన:
y లో x = cos u (u ∈ (0, π)) ను ప్రతిక్షేపిస్తే


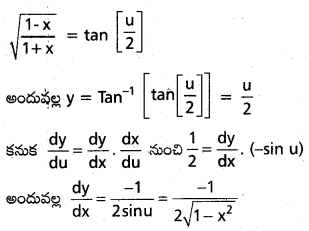
ప్రతిక్షేపణ పద్ధతిలో వివరించిన f(x), g(x), h(u) ల స్థానంలో వరుసగా ఇక్కడ Tan^-1x \(\sqrt{\frac{1-x}{1+x}}\), cos u లు ఉంచామని గమనించండి.

ప్రశ్న 46.
y = Tan^-1 \(\left[\frac{2 x}{1-x^2}\right]\) (|x| < 1) అయితే \(\frac{d y}{d x}\)ను కనుక్కోండి. (A.P. Mar. 15)
సాధన:

ప్రశ్న 47.
x = a cos³ t, y = a sin³ t, అయితే \(\frac{d y}{d x}\)ను కనుక్కోండి.
సాధన:

ప్రశ్న 48.
y = e^t + cos t, x = log t + sin t అయితే \(\frac{d y}{d x}\)ను కనుక్కోండి.
సాధన:
ఇక్కడ \(\frac{d y}{d t}\) = e^t – sin t, \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = \(\frac{1}{t} \cos t\)
కాబట్టి \(\frac{d y}{d x}\) = \(\frac{t\left(e^t-\sin t\right)}{(1+t \cos t)}\)

ప్రశ్న 49.
f(x) = \(x^{\sin ^{-1}} x\) అవకలజాన్ని g(x) = sin^-1 x దృష్ట్యా కనుక్కుని, \(\frac{\mathrm{df}}{\mathrm{dg}}\) ని గుణించండి.
సాధన:

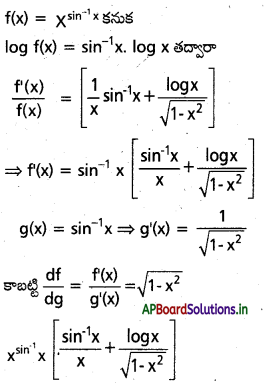
ప్రశ్న 50.
x³ + y³ – 3axy = 0 అయితే \(\frac{d y}{d x}\)ను కనుక్కోండి.
సాధన:
ఇచ్చిన సమీకరణం y = f(x) ప్రమేయాన్ని నిర్వచిస్తుందను కొనుము. అంటే x³ – (f(x))³ – 3ax f(x) = 0
ఈ సమీకరణం రెండు వైపులా x దృష్ట్యా అవకలనం చేస్తే 3x² + 3 (f(x))² f'(x) – [3a. f(x) + 3axf'(x)] = 0
అందువల్ల 3x² + 3y² f'(x) – [3ay + 3ax f'(x)] = 0
కనుక f'(x) = \(\frac{d y}{d x}\) = \(\frac{a y-x^2}{y^2-a x}\)

ప్రశ్న 51.
2x² – 3xy + y² + x + 2y – 8 = 0 అయినప్పుడు \(\frac{d y}{d x}\) కనుక్కోండి.
సాధన:
2x² – 3xy + y² + x + 2y – 8 = 0
y ని x లో ప్రమేయంగా భావించి (1)కి ఇరువైపులా x దృష్ట్యా అవకలనం చేస్తే
4x – 3y – 3xy’ + 2yy’ + 1 + 2y’ = 0.
అందువల్ల \(\frac{d y}{d x}\) = y’ = \(\frac{3 y-4 x-1}{2 y-3 x+2}\)

ప్రశ్న 52.
y = x^x (x > 0) అయినప్పుడు \(\frac{d y}{d x}\)ను కనుక్కోండి.
సాధన:
y = x^xకు ఇరువైపులా సంవర్గమానాలను తీసుకొంటే logy = x log x వస్తుంది. రెండువైపులా X దృష్ట్యా అవకలనం చేస్తే,
\(\frac{y^{\prime}}{y}\) = x. \(\frac{1}{x}\) + log x = 1 + log x.
అందువల్ల \(\frac{d y}{d x}\) = y’ = y(1 + log x)
= x^x (1 + log x)

ప్రశ్న 53.
y = (tan x)^{sin x} [0 < x < \(\frac{\pi}{2}\)] అయితే \(\frac{d y}{d x}\) ను గణించండి.
సాధన:
y = (tan x)^{sin x} కు రెండు వైపులా సంవర్గమానాలు తీసుకొంటే, log y = sin x. log(tan x) వస్తుంది. దీన్ని రెండు వైపులా x దృష్ట్యా అవకలనం చేస్తే
\(\frac{y^{\prime}}{y}\) = \(\frac{\sin x}{\tan x}\). sec²x + cosx. log (tan x)
= sec x + cos x. log (tan x)
అందువల్ల \(\frac{d y}{d x}\)(tan x)^{sin x} [sec x + cos x log (tan x)]