AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Ex 10(h)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(h) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(h)

అభ్యాసం 10 (హెచ్)

I. క్రింది ప్రమేయాలకు వాటి ప్రక్కనే సూచించిన ప్రదేశాలపై స్థానిక అంత్యబిందువులు, స్థానిక అంత్య విలువలు (ఉంటే) కనుక్కోండి.

i) f(x) = x², ∀ x ∈ R.
సాధన:
f(x) = x²
f(x) = 2x = f”(x) = 2
గరిష్టం, కనిష్ట విలువలు f'(x) = 0
2x = 0
x = 0
ఇప్పుడు f”(x) = 2 > 0
∴ f(x) వద్ద x = 0 కనిష్ట విలువ ఉంది.
స్థానిక కనిష్ట బిందువు x’ = 0
స్థానిక కనిష్ట విలువ = 0.

ii) f(x) = sin x, [0, π)
సాధన:
ఇచ్చినది f(x) = sinx
⇒ f'(x) = cosx
⇒ f”(x) = – sin x
గరిష్ట లేక కనిష్ట విలువలు
f'(x) = 0
cos x = 0
⇒ x = \(\frac{\pi}{2}\), \(\frac{3 \pi}{2}\), \(\frac{5 \pi}{2}\), \(\frac{7 \pi}{2}\)

i) \(f^{\prime \prime}\left(\frac{\pi}{2}\right)\) = \(-\sin \frac{\pi}{2}\) = -1 < 0
f(x) = sin \(\frac{\pi}{2}\) = 1
∴ స్థానిక గరిష్ట బిందువు x = \(\frac{\pi}{2}\)
స్థానిక గరిష్ట విలువ x = 1

ii) \(f^{\prime \prime}\left(\frac{3 \pi}{2}\right)\)
= – sin \(\frac{3 \pi}{2}\) = -1 > 0
f(x) = sin \(\frac{3 \pi}{2}\) = -1
∴ స్థానిక కనిష్ట బిందువు x = \(\frac{3 \pi}{2}\)
స్థానిక కనిష్ట బిందువు x = -1

iii) \(f^{\prime \prime}\left(\frac{5 \pi}{2}\right)\)
= -sin \(\frac{5 \pi}{2}\) = -1 < 0
f(x) = sin \(\frac{5 \pi}{2}\) = 1
∴ స్థానిక గరిష్ట బిందువు x = \(\frac{5 \pi}{2}\)
స్థానిక గరిష్ట విలువ x = 1

iv) \(f^{\prime \prime}\left(\frac{7 \pi}{2}\right)\) = -sin \(\frac{7 \pi}{2}\) = 1 > 0
f(x) = sin \(\frac{7 \pi}{2}\) = 1
∴ స్థానిక కనిష్ట బిందువు x = \(\frac{7 \pi}{2}\)
స్థానిక కనిష్ట విలువ x = -1

ii) f(x) = x³ – 6x² + 9x + 15
సాధన:
f'(x) = 3x² – 12x + 9 ⇒ f”(x) = 6x – 12
∴ గరిష్ఠ, కనిష్ఠ విలువలకు f'(x) = 0
⇒ 3x² – 12x + 9 = 0
⇒ x² – 4x + 3 = 0
⇒(x – 1) (x – 3) = 0.
⇒ x = 1 లేదా 3
ఇప్పుడు f”(1) = 6(1) – 12 = -6 < 0
∴ f(x), x = 1 వద్ద గరిష్టము
గరిష్ఠ విలువ f(1)= 1³ – 6 (1)² + 9(1) + 15
= 1 – 6 + 9 + 15 = 19
f”(3) = 6(3) – 12 = 18 – 12 = 6 > 0
∴ f(x), x = 35 g వద్ద కనిష్టము
కనిష్ఠ విలువ = f(3) = 3³ – 6.3² + 9.3 + 15
= 27 – 54 + 27 + 15
= 15

iv) f(x) = \(x \sqrt{(1-x)}\) ∀ x = (0, 1)
సాధన:

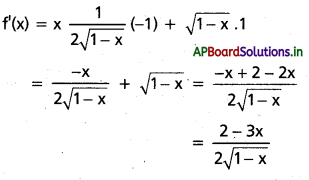
గరిష్ట, కనిష్ట విలువలు f'(x) = 0

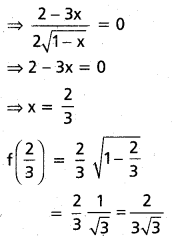
v) f(x) = \(\frac{1}{x^2+2}\) ∀ x ∈ R
సాధన:

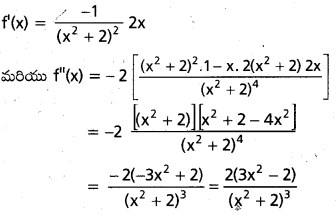
∴ గరిష్ఠ, కనిష్ఠ విలువలకు f'(x) = 0
⇒ \(\frac{-2 x}{\left(x^2+2\right)^2}\) = 0 ⇒ x = 0
f”(0) = \(\frac{2(0-2)}{(0+2)^3}\) = \(\frac{-4}{8}\) = \(\frac{-1}{2}\) < 0
∴ f(x), x = 0 వద్ద గరిష్ఠము
గరిష్ఠ విలువ f(0) = \(\frac{1}{0+2}\) = \(\frac{1}{2}\)

vi) f(x) = x³ – 3x ∀ x ∈R
సాధన:
f'(x) = 3x² – 3 మరియు f'(x) = 6x
∴గరిష్ఠ, కనిష్ట విలువలకు f'(x) = 0
⇒ 3x² – 3 = 0
⇒ x² – 1 = 0
⇒ x = ±1
ఇప్పుడు f”(1) = 6(1) = 6 > 0
∴ f(x), x = 1 ల వద్ద కనిష్ఠము
గరిష్ఠ విలువ f(1) = 1³ – 3 (1) = -2
f”(-1) = 6(-1) = -6 < 0
∴ f(x) కు x = 1 వద్ద గరిష్ఠం
గరిష్ఠ విలువ = f(-1) = (-1)³ – 3(-1)
= -1 + 3 = 2

vii) f(x) = (x – 1)(x + 2)² ∀ x ∈ R
సాధన:
f'(x) = (x – 1) (x + 2)²
f(x) = (x – 1)2(x + 2) + (x + 2)²
= 2(x – 1) (x + 2) + (x + 2)²
f”(x) = 2(x – 1) + 2(x + 2) + 2(x + 2)
= 2(x – 1 + x + 2 + x + 2)
= 2(3x + 3) = 6(x + 1)
∴ గరిష్ఠ, కనిష్ఠ విలువలకు f'(x) = 0
2(x – 1)(x + 2) + (x + 2)² = o
(x + 2) [2(x – 1) + (x + 2)] = 0
⇒ (x + 2) (3x) = 0
⇒ x = 0, x = -2
ఇప్పుడు f”(0) = 6(0 + 1) = 6 > 0
∴ f(x), x = -2 వద్ద కనిష్ఠము
కనిష్ఠ విలువ f(0) = (0 – 1)(0 + 2)² = -4
f”(-2) = 6(-2 + 1) = -6 < 0
∴ f(x), x = -2 వద్ద గరిష్ఠము
గరిష్ఠ విలువ f(-2) = (-2 – 1)(-2 + 2)² = 0

viii) f(x) = \(\frac{x}{2}+\frac{2}{x}\) ∀ x ∈ R
సాధన:
f'(x) = \(\frac{1}{2}\) – \(\frac{2}{x^2}\) మరియు f”(x) = \(\frac{4}{x^3}\)
∴ గరిష్ఠ, కనిష్ఠ విలువలకు f'(x) = 0
⇒ \(\frac{1}{2}-\frac{2}{x^2}\) = 0 ⇒ x² – 4 = 0 ⇒ x = ±2
f”(2) = \(\frac{4}{2^3}\) = \(\frac{1}{2}\) > 0 (x > 0 కనుక)
∴ f(x), x = 2 వద్ద కనిష్ఠ విలువ ఉంది
కనిష్ఠ విలువ = f(2) = \(\frac{2}{2}\) + \(\frac{2}{2}\) = 1 + 1 = 2

ix) f(x) = -(x – 1)³ (x + 1)² ∀ x ∈ R
సాధన:
f(x) = -(x – 1)³ (x + 1)² = (1 – x)³ (x + 1)²
f'(x) = (1 – x)³ 2(x + 1) + 3(1 – x)² (-1) (x + 1)
= (1 – x²) (x + 1) {2(1 – x) – 3(x + 1)}
= (1 – x)²(x + 1){2 – 2x – 3x – 3} = 0
= (1 – x)²(x + 1)(-1 – 5x)
f’'(x) = (1 – x)²(x + 1)(-5) + (1 – x)²(-1 – 5x) + (x + 1)(-1 – 5x) 2(1 – x)(-1)
= -5 (1 – x)² (x + 1) — (1 + 5x) (1 – x)² + (x + 1)(1 + 5x)2(1 – x)
∴ గరిష్ఠ, కనిష్ఠ విలువలకు f'(x) = 0
(1 – x)² (x + 1) (-1 – 5x) = 0
⇒ x = ±1 లేదా -1/5
f’'(1) = 0 – 0 + 0 ⇒ x = 0
f”(1 + 1)²(-1) = 0 – (1 – 5) + 0 = 16 > 0
∴ f(x), x = -1 వద్ద కనిష్ఠం
కనిష్ఠ విలువ f(-1) = (1 + 1)³(-1 + 1)² = o
f”\(\left(-\frac{1}{5}\right)\) < 0
⇒ f(x), x = \(-\frac{1}{5}\) వద్ద గరిష్టము
గరిష్ఠ విలువ f\(\left(-\frac{1}{5}\right)\) = \(\frac{3456}{3125}\)

x) f(x) = x² e^3x x ∈R
సాధన:
f'(x) = x² e^3x . 3 + e^3x. 2x
గరిష్ట, కనిష్ట విలువలు f'(x) = 0
3x² e^3x + 2e^3x.x = 0
x² e^3x (3x + 2) = 0
x = 0, x = \(\frac{-2}{3}\) మరియు e^3x = 0
ఇప్పుడు f”(x) = 3(x² e^3x. 3 + e^3x 2x) + e^3x 2 + 2x e^3x f”(x)
= 9x²e^3x + 6x e^3x + 2 e^3x + 6xe^3x
= 9x²e^3x + 12xe^3x + 2e^3x
f”(0) = 2 > 0
∴ స్థానిక కనిష్ట బిందువు = 0
స్థానిక కనిష్ట విలువ = 0
\(f^{\prime \prime}\left(\frac{-2}{3}\right)\) = \(\frac{-2}{e^2}\) < 0
∴ స్థానిక గరిష్ట బిందువు = \(\frac{-2}{3}\)
స్థానిక గరిష్ట విలువ = \(\frac{4}{9 e^2}\)

II. క్రింది ప్రమేయాలకు వాటి ప్రక్కనే సూచించిన ప్రదేశాలపై గరిష్ఠత్వ, పరమ కనిష్ఠం చూపండి.

i) f(x) = e^x
సాధన:
f'(x) = e^x మరియు f”(x) = e^x
∴ గరిష్ఠ, కనిష్ఠ విలువలకు f'(x) = 0 ⇒ e^x = 0 ⇒ e^x = 0
⇒ x నిర్వచితం కాదు
దత్త ప్రమేయానికి గరిష్ఠ, కనిష్టాలు లేవు.

ii) f(x) = log x (0, ∝)
సాధన:
f'(x) = \(\frac{1}{x}\) మరియు f”(x) = \(-\frac{1}{x^2}\)
f'(x) = 0 = x నిర్వచితం కాదు
⇒ f(x) కు గరిష్ఠ, కనిష్ఠ విలువలు లేవు

iii) f(x) = x³ + x² + x + 1
సాధన:
f(x) = 3x² + 2x + 1 = 0 కు వాస్తవ విలువలు లేవు.
⇒ f(x) కు గరిష్ఠ, కనిష్ఠ విలువలు లేవు.

II. క్రింది ప్రమేయాలకు పక్కనే సూచించిన ప్రదేశాలపై పరమ గరిష్ఠ, పరమ కనిష్ఠ విలువలను (ఉంటే) కనుక్కోండి.

i) f(x) = x³ ; [-2, 2]
సాధన:
f'(x) = 3x² > 0 కనుక f ఆరోహణము f”(x) = 6x
కనిష్ఠ విలువ f(-2) = (-2)³ = 8
గరిష్ఠ విలువ f(2) = 2³ = 8

ii) f(x) = (x – 1)² + 3 ; [-3, 1]
సాధన:
x = 1 వద్ద కనిష్ఠము
కనిష్ఠ విలువ = f(1) = 0 + 3 = 3
(-3, 1) లో f ఆరోహణము రిష్ట విలువ
f(-3) = (-3, -1)² + 3 = 16 + 3 = 19
f(1) = 0 + 3 = 3
గరిష్ఠ విలువ = 19
కనిష్ఠ విలువ = 3

iii) f(x) = 2|x| on [-1, 6]
సాధన:
f'(x) = \(\frac{2|x|}{x}\)
గరిష్ఠ, కనిష్ఠ విలువలు f'(x) = 0
\(\frac{2|x|}{x}\) = 0 ⇒ x = 0
f(0) = 0
f(-1) = 2(-1) = 2
f(6) = 2(6) = 12
కనిష్ఠ విలువ = 0
గరిష్ఠ విలువ = 12

iv) f(x) = sin x + cos x ; [0, π]
సాధన:
f(x) = cos x – sin x ప్రతి x ∈ (0, π) కు వ్యవస్థితం
f'(x) = 0 ⇒ cos x – sin x = 0 కనుక
⇒ tan x = 1
⇒ x = \(\frac{\pi}{4}\) ∈(0,π)
f(0) = sin 0 + cos 0 = 1 కనుక
\(f\left(\frac{\pi}{4}\right)\) = sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\) = \(\frac{2}{\sqrt{2}}\) = \(\sqrt{2}\)
∴ కనిష్ట విలువ -1
గరిష్ఠ విలువ \(\sqrt{2}\)

v) f(x) = x + sin 2x ; [0, 2π]
సాధన:
f(x) = x + sin 2x
f'(x) = 1 + 2 cos 2x
f'(x) = 0 ⇒ 2 cos 2x + 1 = 0
⇒ cos 2x = \(-\frac{1}{2}\) = cos \(\frac{2 \pi}{3}\)
⇒ 2x = \(\frac{2 \pi}{3}\)
⇒ x = \(\frac{\pi}{3}\) ∈ (0, 2π)
f(0) = 0 + sin 2(0) = 0
f\(\left(\frac{\pi}{3}\right)\) = \(\frac{\pi}{3}\) + sin 2. \(\frac{\pi}{3}\) = \(\frac{\pi}{3}\) + \(\frac{\sqrt{3}}{2}\)
f(2π) 2π + sin 2. 2л = 2л + 0 = 2π
కనిష్ట విలువ = 0
గరిష్ఠ విలువ = 2π

ప్రశ్న 2.
మొదటి అవకలజ పరీక్షను ఉపయోగించి f(x) = x³ – 12x ప్రమేయానికి R పై స్థానిక అంత్య విలువలు కనుక్కోండి.
సాధన:
f(x) = x³ – 12x
f(x) = 3x² – 12
f”(x) = 6x
గరిష్ట, కనిష్ట విలువలు f'(x) = 0
3x² – 12 = 0
3x² = 12
x = ± 2
f”(2) = 12 > 0
స్థానిక గరిష్ట బిందువు x = 2
స్థానిక గరిష్ట విలువ = -16
f”(-2) = -12 < 0
స్థానిక గరిష్ట బిందువు x = -1
స్థానిక గరిష్ట విలువ = 16

ప్రశ్న 3.
మొదటి అవకలజ పరీక్షను ఉపయోగించి f(x) = x² – 6x + 8 ∀ x ∈ Rకు స్థానిక అంత్య విలువలను కనుక్కోండి.
సాధన:
f(x) = x² – 6x + 8
f'(x) = 2x – 6 ⇒ f”(x) = 2
గరిష్ట, కనిష్ట విలువకు f(x) = 0.
2x – 6 = 0
x = 3
f”(3) = 2 > 0
x = 3
∴ స్థానిక గరిష్ట బిందువు x = 3
స్థానిక కనిష్ట విలువ = -1

ప్రశ్న 4.
రెండో అవకలజ పరీక్షను ఉపయోగించి f(x) = x³ – 9x² – 48x + 72 ∀ x ∈ Rకు స్థానిక అంత్య విలవులు కనుక్కోండి.
సాధన:
f(x) = x³ – 9x³ – 48x + 72.
f'(x) = 3x² – 18x – 48
= 3(x – 8) (x + 2)
విరామ బిందువులు – 2 & 8
f”(x) = 6x – 18 = 6(x – 3)
At x = 8, f”(8) = 30 > 0.
∴ (8) = (8)³ – 9(8)² – 48(8) + 72
= 512 – 576 – 384 + 72
= -376
At x = -2, f”(-2) = -30 < 0
f(-2) = (-2)³ – 9(-2)² – 48(-2) + 72
= -8 – 36 + 96 + 72
= 124
స్థానిక కనిష్ట బిందువు = -376
స్థానిక గరిష్ట విలువ = 124

ప్రశ్న 5.
రెండో అవకలజ పరీక్షను ఉపయోగించి
f(x) = -x³ + 12x⁵ – 5 ∀ x ∈ R కు స్థానిక అంత్య విలువలు కనుక్కోండి.
సాధన:
f(x) = -x³ + 12x² – 5
⇒ f(x) = -3x² + 24x
= -3x(x – 8)
విరామ బిందువులు 0, 8
f”(x) = -6x + 24
At x = 0, f”(0) = 24 > 0.
f(0) = -5
At x = 8, f”(8) = -24 < 0
f(8) = 8³ + 12(8)² – 5
= -512 + 768 – 5
= 251
స్థానిక కనిష్ట విలువ = -5
స్థానిక గరిష్ట విలువ = 251

ప్రశ్న 6.
\(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) పై నిర్వచితమైన ప్రమేయం f(x) = -sin 2x – x కు స్థానిక గరిష్ట, స్థానిక కనిష్టాలను కనుక్కోండి.
సాధన:
f(x) = -sin 2x – x
f'(x) = -2cos 2x – 1
f”(x) = 4 sin 2x

స్థానిక కనిష్ట విలువ = \(-\frac{\sqrt{3}}{2}\) – \(\frac{\pi}{3}\)
స్థానిక గరిష్ట విలువ = \(\frac{\sqrt{3}}{2}\) + \(\frac{\pi}{3}\)

ప్రశ్న 7.
[0, 5] పై నిర్వచితమైన ప్రమేయం f(x) = 2x³ – 3x² – 36x + 2 కు స్థానిక గరిష్ట, స్థానిక కనిష్టాలను కనుక్కోండి.
సాధన:
f(x) = 2x³ – 3x² – 36x + 2
f(x) = 6x² – 6x – 36
f”(x) = 12x – 6
గరిష్ట, కనిష్ట విలువలు f'(x) = 0
6x² – 6x – 36 = 0
x² – x – 6 = 0
x² – 3x + 2x – 6 = 0
x(x + 3) + 2(x – 3) = 0
(x + 2) (x – 3) = 0
x = 3, -2
f”(3) = 30 > 0
x = 3 వద్ద f(x)కు గరిష్ట/కనిష్ట విలువ
f(3) = 2(3)³ – 3(3)² – 36(3) + 2
= 54 – 27 – 108 + 2
= -79
స్థానిక గరిష్ట విలువ = – 79
0 ≤ x ≤ 5
∴ f(0) = 0 – 0 – 0 + 2
= 2
∴ స్థానిక గరిష్ట విలువ = 2.

ప్రశ్న 8.
[-2, \(\frac{9}{2}\)] పై నిర్వచితమైన ప్రమేయం f(x) = 4x – \(\frac{x^2}{2}\) అంత్య విలువలు కనుక్కోండి.
సాధన:
f(x) = 4x – \(\frac{x^2}{2}\)
f'(x) = 4 – x
f”(x) = -1
గరిష్ట లేదా కనిష్ట విలువ f'(x) = 0
4 – x = 0
x = 4
f”'(4) = −1 <0
x = 4 వద్ద కు గరిష్ట విలువ
f(4) = 16 – \(\frac{16}{2}\) = 8.
∵ -2 ≤ x ≤ \(\frac{9}{2}\)
∴ f(-2) = -8 – \(\frac{4}{2}\)
= -8 – 2 = -10
∴ స్థానిక కనిష్ట విలువ = -10
స్థానిక గరిష్ట విలువ = 8

ప్రశ్న 9.
ఒక కంపెనీ లాభప్రమేయం P(x) = -41 + 72x – 18x² అయితే కంపెనీ గరిష్ట లాభాన్ని కనుక్కోండి.
సాధన;
P(x) = -41 + 72x – 18x²
\(\frac{d p(x)}{d x}\) = 72 – 36x
గరిష్ట లేదా కనిష్ట విలువ
72 – 36x = 0
x = 2
\(\frac{d^2 p}{d x^2}\) = -36′ < 0
∴ x = 2 వద్ద f(x) కు గరిష్ట లాభం
గరిష్ట లాభం P(2) = -41 + 72(2) – 18(4)
= 31

ప్రశ్న 10.
ఒక కంపెనీ ఒక వస్తువును x యూనిట్లను అమ్మితే వచ్చే P(x) = -x² + 9x² – 15x – 13 (x యూనిట్లు వెలలో) ఆ కంపెనీ 6000 వస్తువులను తయారు (ఉత్పత్తి) చేసే సామర్థ్యం ఉంటే గరిష్ట లాభాన్ని కనుక్కోండి.
సాధన:
P(x) = -x³ + 9x² – 15x – 13
\(\frac{\mathrm{dp}(\mathrm{x})}{\mathrm{dx}}\) = -3x² + 18x – 15
గరిష్ట, కనిష్ట విలువలు \(\frac{d p}{d x}\) = 0
-3x² + 18x – 15 = 0
x² – 6x + 5 = 0
x² – 5x – x + 5 = 0
x(x – 5) – 1(x – 5) = 0
(x – 1) (x – 5) = 0
x = 1, 5
P(1) = -1 + 9 – 15 – 13 = -10
P(5) = -125 + 225 – 75 – 13 = 12
∴ గరిష్ట లాభం = 12.

III.

ప్రశ్న 1.
ఒక కంపెనీ రోజుకు X సంఖ్యలో ఒక వస్తువును అమ్మితే వచ్చే లాభ ప్రమేయం P(x) = (150 – x) x – 1000. అది గరిష్ట లాభాన్ని పొందడానికి కంపెనీ ఆ వస్తువును ఎన్ని తయారు (ఉత్పత్తి) చేయాలి. గరిష్ట లాభాన్ని కూడా కనుక్కోండి.
సాధన:
లాభ ప్రమేయం
P(x) = (150 – x) x – 1000.
గరిష్ట లేదా కనిష్ట విలువ \(\frac{d p}{d x}\) = 0
(150 – x(1) – x (-1) = 0
150 – 2x = 0
x = 75
\(\frac{d^2 p}{d x^2}\) = -2 < 0
∴ x = 75 వద్ద గరిష్ట లాభం
గరిష్ట లాభాన్ని పొందటానికి కంపెనీ 75 వస్తువులు అమ్మాలి.
గరిష్ట లాభం P(75) = 4625.

ప్రశ్న 2.
f(x) = 8x³ + 81x² – 42x – 8 ∀ x ∈ R [-8, 2] పరమ గరిష్టం, పరమ కనిష్టాలను కనుక్కోండి.
సాధన:
f(x) = 8x³ + 81x² – 42x – 8.
f'(x) = 24x² + 162x – 42 = 0
గరిష్ట, కనిష్ట విలువలు f(x) = 0
24x² + 162x – 42 = 0
4x² + 27x – 7 = 0
4x² + 28x – x – 7 = 0
4x(x + 7) – 1(x + 7) = 0
(x + 7) (4x – 1) = 0
x = – 7 లేదా \(\frac{1}{4}\)
f(-8) = 8(-8)³ + 81(-8)² – 42(-8) – 8
= -8(512) + 81(64) + 336 – 8
= – 4096 + 5184 + 336 – 8
= 5520 – 4104 = 1416
f(2) = 8(2)³ + 81(2)² – 42(2) – 8
= 64 + 324 – 84 – 8
= 296

పరమ గరిష్ట విలువ = 1416
పరమ కనిష్ట విలువ = \(\frac{-213}{16}\)

ప్రశ్న 3.
రెండు సంఖ్యల మొత్తం 16గా ఉంటూ వాటి వర్గాల మొత్తం కనిష్టంగా ఉండే సంఖ్యలను కనుక్కోండి.
సాధన:
x, yలు రెండు సంఖ్యలు అనుకోండి.
x + y = 16
⇒ у = 16 – x
f(x) = x² + y² = x² + (16 – x)²
= x² + 256 + x² – 32x
f'(x) = 4x – 32
కనిష్ట, గరిష్ట విలువలు f'(x) = 0
⇒ 4x – 32 = 0
4x = 32
x = 8
f”(x) = 4 > 0
∴ x = 8 వద్ద f(x) కనిష్ఠం
y = 16 – x = 16 – 8 = 9
∴ కావలసిన సంఖ్యలు 8, 8.

ప్రశ్న 4.
x + y = 60, xy³ మహిష్ఠం అయ్యేటట్లుగా రెండు ధనాత్మక సంఖ్యలు x, y లను కనుక్కోండి ధనాత్మక సంఖ్యలు x, y లను కనుక్కోండి. (A.P Mar. ’15)
సాధన:
x + y = 60 ⇒ y = 60 – x – (1)
p = xy³ = x(60 – x)³.
= -3(60 – x)²(-1) + (60 – x)³
=-3x (60 – x)² + (60 – x)³
= (60 – x)² – 3x + 60 – x]
= (60 – x)² (60 – 4x) = 4(60 – x)² (15 – x)
\(\frac{d^2 p}{d x^2}\) = 4[(60 – x)² (-1) + (15 – x) 2(60 – x) (-1)].
= 4(60 – x) [-60 + x – 30 + 2x]
= 4(60 – x) (3x – 90)
= 12 (60 – x) (x – 30)
గరిష్ట, కనిష్ట విలువలు \(\frac{\mathrm{dp}}{\mathrm{dx}}\) = 0
⇒ 4(60 – x)² (15 – x) = 0
⇒ 4(60 – x)² (15 – x) = 0
⇒ x = 60 లేదా x = 15 ; x అనేది 60 అవ్వదు.
∴ x = 15 ⇒ y = 60 – 15 = 45
\(\left(\frac{d^2 p}{d x^2}\right)_{x=15}\) = 12(60 – 15) (15 – 3x) < 0
⇒ p గరిష్టము
∴ కావలసిన సంఖ్యలు 15, 45.

ప్రశ్న 5.
30 సెం.మీ × 80 సెం.మీ కొలతలుగా ఉండే ఒక దీర్ఘచతురస్రాకారపు రేకు ముక్క నాలుగు మూలల నుంచి x భుజంగా ఉండే చతురస్రాకార ముక్కలను కత్తిరించి మిగిలిన రేకులు మడిచి మూతలేని పెట్టెను తయారుచేశారు. ఆ పెట్టె ఘనపరిమాణం గరిష్టం అయితే x విలువ కనుక్కోండి ? (Mar. ’14)
సాధన:
పెట్టె యొక్క పొడవు = 80 – 2x = l
పెట్టె యొక్క వెడల్పు = 30 – 2x = b

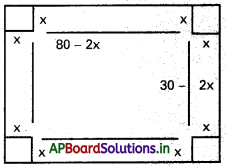
పెట్టె ఎత్తు = x = h
ఘన పరిమాణము = lbh= (80 – 2x) (30 – 2x). x
= x (2400 – 220 x + 4x²)
f(x) = 4x³ – 220x² + 2400x
f”(x) = 12x² – 440x + 2400
= 4[3x² – 110 x + 600]
f’ (x) = 0 = 3x² – 110x + 600 = 0
x = \(\frac{110 \pm \sqrt{12100-7200}}{6}\)
= \(\frac{110 \pm 70}{6}\) = \(\frac{180}{6}\) లేదా \(\frac{40}{6}\) = \(\frac{30}{3}\) లేదా \(\frac{20}{3}\)
x = 30, b = 30 – 2x = 30 – 2 (30) = -30 < 0 అయితే
⇒ x ≠ 30
∴ x = \(\frac{20}{3}\)
f”(x) = 24x – 440
x = \(\frac{20}{3}\), అయితే f”(x) = 24. \(\frac{20}{3}\) – 440
= 160 – 440
= -280 < 0
f(x) విలువ x = \(\frac{20}{3}\) వద్ద గరిష్టము
x = \(\frac{20}{3}\) సెం. మీ వద్ద పెట్టె ఘనపరిమాణము గరిష్టము

ప్రశ్న 6.
దీర్ఘచతురస్రంపై అర్థవృత్తం ఉన్న ఆకారంలో ఉన్న కిటికీ చుట్టుకొలత 20 అడుగులు ఉండేటట్లు తయారుచేసే కిటికీలన్నింటికీ వైశాల్యాలలో గరిష్ఠ వైశాల్యాన్ని కోరుక్కోండి. (T.S Mar. ’15)
సాధన:
ఒక దీర్ఘచతురస్రం యొక్క పొడవు = 2x అనుకొనుము. మరియు వెడల్పు = y అనుకుంటే అర్ధవృత్తం యొక్క వ్యాసార్థం = x అవుతుంది.

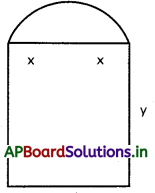
చుట్టుకొలత = 2x + 2y + π. x = 20
2y = 20 – 2x – πx
y = 10 – x – \(\frac{\pi}{2} \cdot x\)
వైశాల్యం = 2xy + \(\frac{\pi}{2} \cdot x^2\)
= 2x \(\left(10-x-\frac{\pi x}{2}\right)\) + \(\frac{\pi}{2} x^2\)
= 20x – 2x² – πx² + \(\frac{\pi}{2} \mathrm{x}^2\)
f(x) = 20x − 2x² – \(\frac{\pi}{2} x^2\)
f'(x) = 0 ⇒ 20x – 2x² – \(\frac{\pi}{2} x^2\)
f'(x) = 0 ⇒ 20 – 4x – πx = 0
(π + 4) x = 20
x = \(\frac{20}{\pi+4}\)
f”(x) = -4 – π < 0
f(x) ను గరిష్ఠం అనుకుంటే x = \(\frac{20}{\pi+4}\)

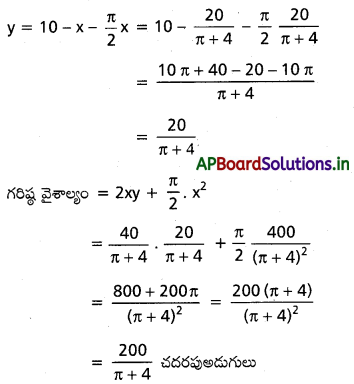
ప్రశ్న 7.
వ్యాసార్ధం గల గోళంలో అంతర్లిఖిత స్థూపాలలో (లంబవృత్త) వక్రతల వైశాల్యం గరిష్ఠమయ్యే స్థూపం ఎత్తు \(\sqrt{2}\)r అని చూపండి. (May ’11 ’13; Mar. ’13, ’08, ’04; June ’04)
సాధన:
స్థూపం వ్యాసార్ధము r, ఎత్తు h, అనుకొందాం.

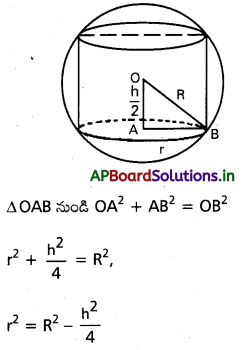
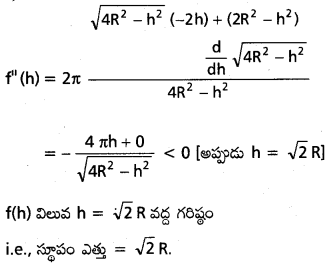
ప్రశ్న 8.
l పొడవు ఉండే తీగను రెండు ముక్కలు చేసి ఒక ముక్కను చతురస్రాకారంగాను, రెండో ముక్కను వృత్తాకారంగాను వంచగా ఏర్పడిన వైశాల్యాల మొత్తం అల్పిష్ఠం కావాలంటే ఆ ముక్కల పొడవు ఎంత ?
సాధన:
చతురస్రం భుజము X, వృత్త వ్యాసార్ధం r, అనుకొందాం.

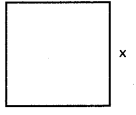
4x + 2πr = l అని ఇవ్వబడింది.
4x = l – 2πr
x = \(\frac{l-2 \pi \mathrm{r}}{4}\)
వైశాల్యాల మొత్తం = x² + πr²


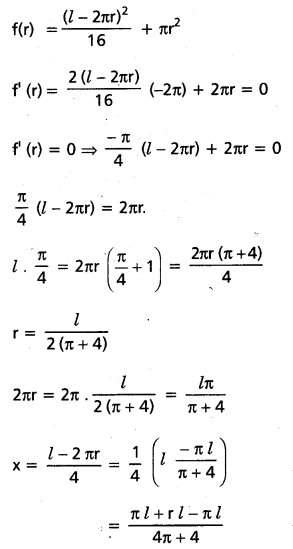
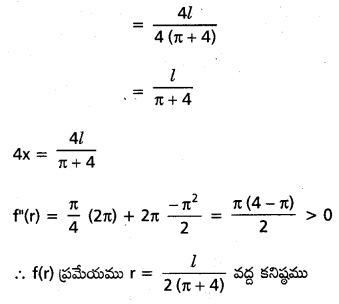
ఇచ్చిన తీగ \(\frac{\pi l}{\pi+4}\) మరియు \(\frac{4 l}{\pi+4}\) ముక్కలుగా విడగొడితే వైశాల్యాల మొత్తము కనిష్ఠము.