AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Ex 3(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 3 సరళరేఖ Exercise 3(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Exercise 3(a)

అభ్యాసం – 3 (ఎ)

I.

ప్రశ్న 1.
x + y = 0, x – y = 0 రేఖల వాలులు కనుక్కోండి.
సాధన:
x + y = 0 రేఖ వాలు – \(\frac{a}{b}\) = -1
x – y = 0 రేఖ వాలు = 1

ప్రశ్న 2.
(2, -3), (0, -3) బిందువులు ఉండే రేఖ సమీకరణం కనుక్కోండి.
సాధన:
రేఖ సమీకరణము
(y – y₁) (x₁ – x₂) = (x – x₁) (y₁ – y₂)
(y + 3) (2 – 0) = (x – 2) (-3 + 3)
2(y + 3) = 0
= y + 3 = 0

ప్రశ్న 3.
(1, 2), (1, -2) బిందువులు ఉండే రేఖ సమీకరణం కనుక్కోండి.
సాధన:
రేఖ సమీకరణం
(y – y₁) (x₁ − x₂) = (x – x₁) (y₁ – y₂)
(y – 2) (1 – 1) = (x – 1) (2 + 2)
0 = 4(x – 1)
x – 1 = 0.

ప్రశ్న 4.
సరళరేఖ y = \(\sqrt{3}\)x – 4 Y – అక్షంతో చేసే కోణం, కనుక్కోండి.
సాధన:
రేఖ సమీకరణము y = \(\sqrt{3}\)x – 4
వాలు = m = \(\sqrt{3}\) = tan \(\frac{\pi}{3}\)
X- అక్షంతో చేసే కోణం = \(\frac{\pi}{3}\)
Y- అక్షంతో చేసే కోణం = \(\frac{\pi}{2}\) – \(\frac{\pi}{3}\) = \(\frac{\pi}{6}\)

ప్రశ్న 5.
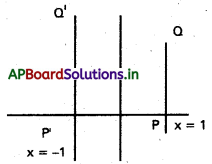
Y- అక్షంలో X = 1 రేఖకు ప్రతిబింబం సమీకరణం కనుక్కోండి.
సాధన:
PQ సమీకరణము x = 1
Y-అక్షం దృష్ట్యా X = -1 యొక్క ప్రతిబింబము
i.e., x + 1 = 0

ప్రశ్న 6.
ab = 0 అయినప్పుడు (a, 0), (h, k), (0, b) బిందువులు సరేఖీయాలు కావడానికి నియమం కనుక్కోండి.
సాధన:
A(a, 0), B(h, k), C(0, b) లు సరేఖీయాలు.
⇒ AB వాలు = AC వాలు
\(\frac{k-0}{h-a}=\frac{-b}{a}\)
ak = – bh + ab
bh + ak = ab
\(\frac{h}{a}+\frac{k}{b}\) = 1

ప్రశ్న 7.
X- అక్షానికి సమాంతరంగా ఉంటూ
i) X- అక్షానికి ఎగువన 3 యూనిట్ల దూరంలో
ii) X- అక్షానికి దిగువన 4 యూనిట్ల దూరంలో ఉన్న సరళరేఖల సమీకరణాలు రాయండి.
సాధన:
i)

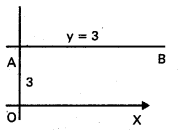
AB సమీకరణము y = 3

ii)

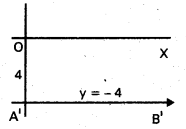
AB సమీకరణము y = -4
y + 4 = 0

ప్రశ్న 8.
Y- అక్షానికి సమాంతరంగా ఉంటూ
i) Y- అక్షానికి కుడివైపున 2 యూనిట్ల దూరంలో
ii) Y- అక్షానికి ఎడమవైపున 5 యూనిట్ల దూరంలో ఉన్న సరళరేఖల సమీకరణాలను రాయండి.
సాధన:
i)

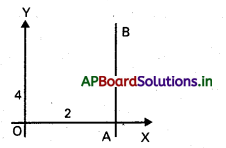
కావలసిన AB సమీకరణము X = 2 లేదా X – 2 = 0

ii)

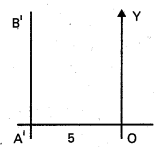
కావలసిన AB సమీకరణము
x = -5
x + 5 = 0

II.

ప్రశ్న 1.
క్రింద ఇచ్చిన బిందు యుగ్మాల ద్వారా పోయే సరళరేఖల వాలులు కనుక్కోండి.
i) (-3, 8) (10, 5)
ii) (3, 4) (7, -6)
iii) (8, 1), (-1, 7)
iv) (-p, q) (q, -p) (pq ≠ 0)
సాధన:
i) వాలు = \(\frac{y_1-y_2}{x_1-x_2}=\frac{8-5}{-3-10}=\frac{-3}{13}\)
ii) వాలు = \(\frac{4+6}{3-7}=\frac{10}{-4}=\frac{-5}{2}\)
iii) వాలు = \(\frac{1-7}{8+1}=\frac{-6}{9}=\frac{-2}{3}\)
iv) వాలు = \(\frac{q+p}{-p-q}=\frac{(p+q)}{-(p+q)}=-1\)

ప్రశ్న 2.
(2, 5), (x, 3) బిందువులగుండా పోయే సరళరేఖ వాలు 2 అయితే X విలువ కనుక్కోండి.
సాధన:
వాలు = \(\frac{y_1-y_2}{x_1-x_2}=\frac{5-3}{2-x}\) = 2
2 = 2(2 – x) ⇒ 1 = 12 – x
x = 2 – 1 = 1

ప్రశ్న 3.
(3, y), (2, 7) బిందువులను కలిపే రేఖ (−1, 4), (0, 6) బిందువులను కలిపే రేఖకు సమాంతరంగా ఉంటే y విలువ కనుక్కోండి. [Mar. ’14]
సాధన:
A(3, y), B(2, 7), P (-1, 4), Q(0, 6) లు దత్త బిందువులు.
m₁ = AB వాలు = \(\frac{y-7}{3-2}\) = y – 7
m₂ = PQ వాలు = \(\frac{4-6}{-1-0}=\frac{-2}{-1}\) = 2

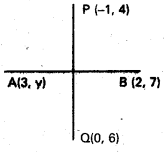
AB, PQ లు సమాంతరాలు.
m₁ = m₂ ⇒ y – 7 = 2
y = 2 + 7 = 9

ప్రశ్న 4.
(6, 3), (- 4, 5) బిందువుల గుండా పోయే రేఖకు
(i) సమాంతరంగా
(ii) లంబంగా ఉన్న సరళరేఖల వాలులు కనుక్కోండి.
సాధన:
(6, 3), B(-4, 5) లు దత్త బిందువులు.
m = AB వాలు = \(\frac{3-5}{6+4}=\frac{-2}{10}=-\frac{1}{5}\)

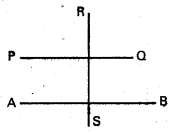
PQ కు సమాంతరం AB
PQ వాలు = m = –\(\frac{1}{5}\)
RS కు లంబంగా AB
RS వాలు = – \(\frac{1}{m}\) = 5

ప్రశ్న 5.
ధన X-అక్షంతో ధనదిశలో క్రింద ఇచ్చిన కోణాలు చేస్తూ, దత్త బిందువు గుండా పోయే సరళరేఖల సమీకరణాలు కనుక్కోండి.
i) \(\frac{\pi}{4}\), (0,0)
ii) \(\frac{\pi}{3}\), (1, 2)
ili) 135°, (3, -2)
iv) 150°, (-2, -1)
సాధన:
i) m = వాలు = tan 45° = 1
రేఖా సమీకరణము y – y₁ = m(x – x₁)
y – 0 = 1(x – 0)
i.e., y = x
లేదా x – y = 0

ii) m = tan 60° = \(\sqrt{3}\)
రేఖా సమీకరణము
y – 2 = \(\sqrt{3}\)(x – 1)
= \(\sqrt{3}\)x – \(\sqrt{3}\)
\(\sqrt{3}\)x – y +(2 – \(\sqrt{3}\)) = 0

iii) m = tan 135° tan (180° – 45°)
– tan 45° = -1 .
రేఖా సమీకరణము y + 2 = 1 (x + 3)
= – x + 3
i.e., x + y – 1 = 0

iv) m = tan 150 ° = tan (180° – 30)
= -tan 30° = –\(\frac{1}{\sqrt{3}}\)
రేఖా సమీకరణము
y + 1 = –\(\frac{1}{\sqrt{3}}\) (x + 2)
\(\sqrt{3}\)y + \(\sqrt{3}\) = -x – 2
x + \(\sqrt{3}\)y + (2 + \(\sqrt{3}\)) = 0

ప్రశ్న 6.
మూల బిందువు గుండాపోతూ నిరూపకాక్షాలతో సమాన కోణాలు చేసే సరళరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
సందర్భం (i) : PP’ రేఖ X – అక్షం ధన దిశలో 45° కోణం చేస్తుంది.
m = tan 45° = 1
PP’ రేఖ (0, 0) గుండా పోతుంది.
PP’ సమీకరణము y – 0 = 1(x – 0)
y = x

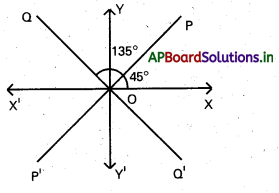
సందర్భం ii) : QQ’ రేఖ X – అక్షం ధన దిశలో 135° కోణం చేస్తుంది.
m = tan 135° =tan (180° – 45°) = -tan 45°
QQ’ సమీకరణము y – 0 = -1(x – 0)
y = -x

ప్రశ్న 7.
సరళరేఖ ధన X- అక్షం ధన దిశతో చేసే కోణం, దాని Y-అంతర ఖండం క్రింద ఇచ్చాం. ఆ సరళరేఖ సమీకరణం కనుక్కోండి.
i) 60°, 3
ii) 150°, 2
iii) 45°, -2
iv) tan^-1 \(\left(\frac{2}{3}\right)\), 3
సాధన:
i) రేఖ సమీకరణము y = mx + c
m = tan 60° = \(\sqrt{3}\), c = 3
రేఖ సమీకరణము y = \(\sqrt{3}\)x + 3
\(\sqrt{3}\)x – y + 3 = 0

ii) m = tan 150° = tan (180° – 30°)
= – tan 30° = \(\frac{-1}{\sqrt{3}}\), c = 2
రేఖ సమీకరణము y = −x + 2
\(\sqrt{3}\)y = -x + 2\(\sqrt{3}\)
x + \(\sqrt{3}\)y – 2\(\sqrt{3}\) = 0

iii) m = tan 45° = 1
c = -2
రేఖ సమీకరణము
y = x – 2
x – y – 2 = 0

iv) θ = tan^-1 \(\left(\frac{2}{3}\right)\) ⇒ m = tan θ = \(\frac{2}{3}\), c = 3
రేఖా సమీకరణము y = \(\frac{2}{3}\)x + 3
3y = 2x + 9
2x – 3y + 9 = 0

ప్రశ్న 8.
(- 4, 5) బిందువుగుండా పోతూ నిరూపకాక్షాలలో సమాన శూన్యేతర అంతరఖండాలు చేసే సరళరేఖ సమీకరణం కనుక్కోండి. [T.S Mar. ’15; May ’13]
సాధన:
అంతరఖండ రూపంలో సరళరేఖ సమీకరణము
\(\frac{x}{a}+\frac{y}{b}\) = 1
దత్తాంశము ప్రకారము a = b
రేఖా సమీకరణము \(\frac{x}{a}+\frac{y}{b}\) = 1
⇒ x + y = a
ఈ రేఖ P(- 4, 5) గుండా పోతుంది.
– 4 + 5 = a ⇒ a = 1
కావలసిన రేఖ సమీకరణము
x + y = 1
లేదా x + y – 1 = 0

ప్రశ్న 9.
(-2, 4) బిందువు గుండా పోతూ శూన్యేతర అంతర ఖండాల మొత్తము సున్న అయ్యే సరళరేఖ సమీకరణం కనుక్కోండి. [A.P Mar. ’15]
సాధన:
అంతరఖండ రూపంలో రేఖ సమీకరణము
\(\frac{x}{a}+\frac{y}{b}\) = 1
దత్తాంశము ప్రకారం a + b = 0 ⇒ b = -a
రేఖ సమీకరణము \(\frac{x}{a}-\frac{y}{a}\) = 1
⇒ x – y = a
ఈ రేఖ P(−2, 4) గుండా పోతుంది.
∴ -2 – 4 = a ⇒ a = -6
కావలసిన రేఖ సమీకరణము x – y = -6
x − y + 6 = 0

III.

ప్రశ్న 1.
(3, – 4) బిందువు గుండా పోతూ X, Y- అంతరఖండాలు 2:3 నిష్పత్తిలో గల సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
అంతరఖండ రూపంలో రేఖ సమీకరణము
\(\frac{x}{a}+\frac{y}{b}\) = 1
దత్తాంశం ప్రకారం \(\frac{a}{b}=\frac{2}{3}\) ⇒ b = \(\frac{3 a}{2}\)
రేఖ సమీకరణం \(\frac{x}{a}+\frac{2 y}{3 a}\) = 1
3x + 2y = 3a
ఈ రేఖ P(3, – 4) గుండా పోతుంది.
9 – 8 = 3a ⇒ 3a = 1
కావలసిన రేఖ సమీకరణము 3x + y = 1
3x + 2y – 1 = 0

ప్రశ్న 2.
(4, -3) బిందువు గుండా పోతూ (1, 1), (2, 3) బిందువుల ద్వారా పోయే సరళరేఖకు లంబంగా ఉండే సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
A(1, 1); B(2, 3) లు దత్త బిందువులు.
m = AB వాలు = \(\frac{1-3}{1-2}=\frac{-2}{-1}\) = 2

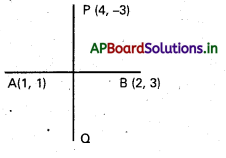
PQ రేఖ AB కి లంబంగా ఉంది.
PQ వాలు = – \(\frac{1}{m}\) = –\(\frac{1}{2}\)
PQ రేఖ (4, -3) గుండా పోతుంది.
PQ సమీకరణము y – y₁ = m(x – x₁)
y + 3 = –\(\frac{1}{2}\) (x – 4)
2y + 6 = -x + 4
x + 2y + 2 = 0

ప్రశ్న 3.
కింది బిందువులు సరేఖీయాలని చూపి కలిగి ఉండే L సరళరేఖ సమీకరణం కనుక్కోండి.
i) (-5, 1), (5, 5), (10, 7)
ii) (1, 3), (-2, -6), (2, 6)
iii) (a, b + c), (b, c + a), (c, a + b)
సాధన:
i) A(-5, 1), B(5, 5), C(10, 7) లు దత్త బిందువులు.
AB సమీకరణము
(y – y₁) (x, – x₂) = (x – x₁) (y₁ – y₂)
(y – 1) (-5 – 5) = (x + 5) (1 – 5)
-10y + 10 = -4x – 20
4x – 10y + 30 = 0
లేదా 2x – 5y + 15 = 0
C (10, 7)
2x – 5y + 15 = 2.10 – 5.7 + 15
= 20 – 35 + 15 = 0
A,B,C లు సరేఖీయాలు.
దత్త బిందువుల గుండా పోయే రేఖ సమీకరణం
2x – 5y + 15 = 0

ii) A(1, 3), B(-2, -6), C(2, 6)
AB సమీకరణం
(y – 3)(1 + 2) = (x – 1) (3 + 6)
3(y – 3) = 9(x – 1)
y – 3 = 3x – 3
3x – y = 0
C(2, 6)
3x – y = 3.2 – 6 = 6 – 6 = 0
∴ దత్త బిందువులు A, B, C లు సరేఖీయాలు,
A,B,C ల గుండా పోయే రేఖ సమీకరణము
3x – y = 0

iii) A(a, b + c), B(b, c + a), C(c, a + b)
AB సమీకరణము
(y – (b + c)) (a – b) = (x – a) (b + c – c – a)
(y – b – c) (a – b) = -(a – b) (x − a)
y – b – c = -x + a
లేదా x + y – (a + b + c) = 0
C(c, a + b)
c + a + b – a – b – c = 0
బిందువు AB మీద ఉంది.
A, B, C లు సరేఖీయాలు.
ఈ రేఖ సమీకరణము x + y = a + b + c

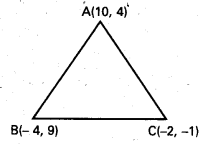
ప్రశ్న 4.
ఒక త్రిభుజానికి A(10, 4), B(-4, 9), C(-2, -1) లు శీర్షాలు.
i) \(\overleftrightarrow{A B}\)
ii) A ద్వారా పోయే మధ్యగత రేఖ
iii) B ద్వారా పోయే ఉన్నతి
iv) భుజం \(\overleftrightarrow{A B}\) కి లంబ సమద్విఖండన రేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
i) A(10, 4), B(-4, 9)లు దత్త బిందువులు.
AB సమీకరణము
(y – 4) (10 + 4) = (x – 10) (4 – 9)
14y – 56 = -5x + 50
5x + 14y – 106 = 0

ii) D బిందువు BC మధ్య బిందువు
D నిరూపకాలు \(\left(\frac{-4-2}{2}, \frac{9-1}{2}\right)\)
= (-3, 4)

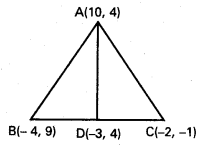
A (10, 4) మూడవ శీర్షంలో AD సమీకరణం
(y – 4) (10 + 3) = (x + 3) (4 −4)
13(y – 4) = 0 ⇒ y – 4 = 0 (లేదా) y = 4

iii)

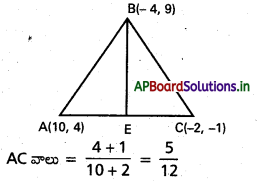
BE రేఖ AC కి లంబంగా ఉంది.
BE వాలు = \(\frac{-1}{m}=\frac{-12}{5}\)
BE రేఖ B(-4, 9) గుండా పోతుంది.
BE సమీకరణం ఉన్నతి
y – 9 = \(\frac{-12}{5}\) (x + 4)
5y – 45 = -12x – 48
12x + 5y + 3 = 0

iv) మధ్య బిందువు AB

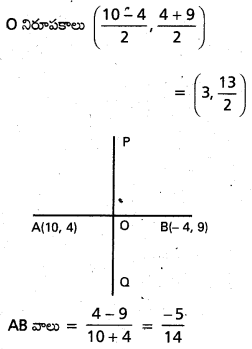
PQ రేఖ AB కి లంబంగా ఉంది.
PQ వాలు = \(\frac{-1}{m}=\frac{14}{5}\)
AB లంబ సమద్విఖండన రేఖ సమీకరణము
У – \(\frac{13}{2}\) = \(\frac{14}{5}\) (x – 3)
5y – \(\frac{65}{2}\) = 14x – 42
14x – 5y + \(\left(\frac{65}{2}-42\right)\) = 0
14x – 5y – \(\frac{19}{2}\) = 0
28x – 10y – 19 = 0