AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Ex 3(c)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 3 సరళరేఖ Exercise 3(c) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Exercise 3(c)

అభ్యాసం – 3 (సి)

I.

ప్రశ్న 1.
కింద సూచించిన సరళరేఖలు దత్త బిందువులను కలిపే రేఖాఖండాలను విభజించే నిష్పత్తులను కనుక్కోండి. ఆ బిందువులు సరళరేఖకు ఒకే వైపున ఉన్నాయో, చెరొక వైపున ఉన్నాయో తెలపండి.
i) 3x −4y=7, (2, -7), (−1, 3)
సాధన:
3x – 4y – 7 = 0

L₁₁, L₂₂ లు వ్యతిరేక గుర్తులు కలిగి వున్నాయి.

ii) 3x + 4y = 6, (2, -1), (1, 1)
సాధన:
సరళరేఖ సమీకరణము 3x + 4y – 6 = 0

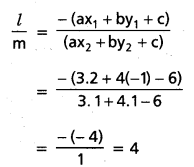
దత్త బిందువులు రేఖకు వ్యతిరేక దిశలలో ఉంటాయి.

iii) 2x + 3y = 5, (0, 0), (-2, 1) [Mar. ’14]
సాధన:
2x + 3y – 5 = 0.
\(\frac{l}{m}=\frac{-(0+0-5)}{-4+3-5}\)
= \(\frac{-5}{6}\)
దత్త బిందువులు రేఖకు ఒకే వైపున ఉంటాయి.

ప్రశ్న 2.
కింది రేఖల ఖండన బిందువును కనుక్కోండి.

i) 4x + 8y 1 = 0, 2x − y + 1 = 0
సాధన:
4x + 8y – 1 = 0, 2x – y + 1 = 0
ఖండన బిందువు

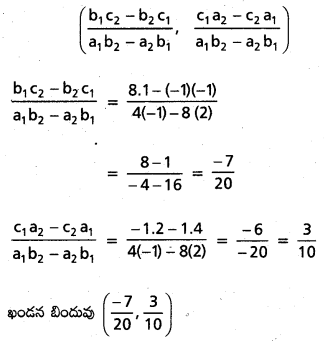
ii) 7x + y + 3 = 0, x + y = 0
సాధన:
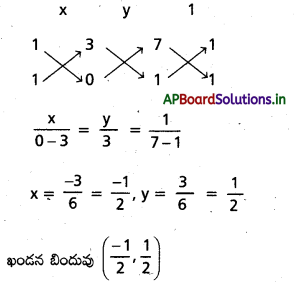
7x + y + 3 = 0, x + y = 0

ప్రశ్న 3.
(a – b) x + (b – c) y = c – a, (b – c)x + (c – a)y = (a – b), (c – a)x + (a – b)y b – c సరళరేఖలు అనుషక్తాలని చూపండి.
సాధన:
దత్త రేఖల సమీకరణాలు
(a – b) x + (b – c) y = c – a ……………… (1)
(b-c) x + (c – a) y = a – b ……………… (2)
(c – a) x + (a – b) y = b – c …………….. (3)
(1), (2) ల నుండి


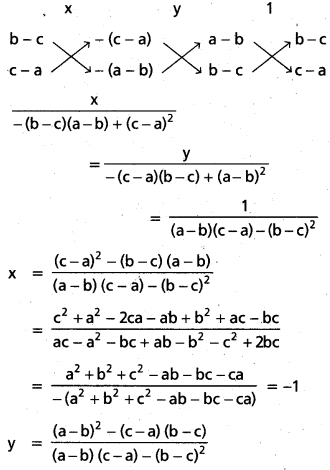
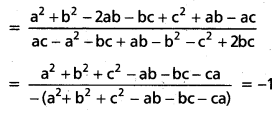
(1), (2) ల ఖండన బిందువు P (-1, -1)
(3) లో ప్రతిక్షేపించగా
(c − a) (-1) + (a – b) (−1) = c + a – a + b = b – c
∴ P (−1, −1) బిందువు (3) మీద ఉంది.
దత్త రేఖలు అనుషక్తాలు.

ప్రశ్న 4.
కింద ఇచ్చిన సమీకరణాలను L₁ + λL₂ = 0 రూపంలోకి మార్చండి. ఈ సమీకరణం సూచించే సరళరేఖా కుటుంబం అనుషక్త బిందువును కనుక్కోండి.
i) (2 + 5k)x – 3(1 + 2k)y + (2 − k) = 0
సాధన:
(2 + 5k)x − 3(1 + 2k)y + (2 – k) = 0
(2x – 3y+ 2) + k (5x – 6y – 1) = 0
ఇది L₁ + λL₂ = 0 రూపంలో ఉంది.
L₁ = 2x – 3y + 2 = 0
L₂ = 5x – 6y – 1 = 0

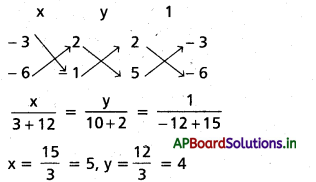
P(5, 4) అనుషక్త బిందువు.

ii) (k + 1)x + (k + 2) y + 5 = 0
సాధన:
(k + 1)x + (k + 2) y + 5 = 0
k (x + y) + (x + 2y + 5) = 0
i.e., (x + 2y + 5) + k (x + y) = 0
ఇది L₁ + λL₂ = 0 రూపంలో ఉంది.
∴ L₁ = x + 2y + 5 = 0
L₂ = x + y = 0

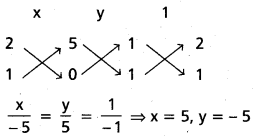
అనుషక్త బిందువు P(5, – 5).

ప్రశ్న 5.
x + p = 0, y + 2 = 0, 3x + 2y + 5 = 0 సరళరేఖలు అనుషకాలయితే p విలువను కనుక్కోండి. [Mar. ’13]
సాధన:
దత్తరేఖల సమీకరణాలు
x + p = 0 …………… (1)
y + 2 = 0 …………… (2)
3x + 2y + 5 = 0 ……………… (3)
(2) నుండి y = -2
(3) లో ప్రతిక్షేపించగా 3x – 4 + 5 = 0
3x = 4 – 5 = -1
x = –\(\frac{1}{3}\)
(2), (3) ల ఖండన బిందువు P(-\(\frac{1}{3}\), 2)
దత్త రేఖలు అనుషక్తాలు.
బిందువు x + p = 0 పై ఉంది.
–\(\frac{1}{3}\) + p = 0 ⇒ p = \(\frac{1}{3}\)

ప్రశ్న 6.
నిరూపకాక్షాలతోను, కింద సూచించిన సరళరేఖలతోను ఏర్పడే త్రిభుజ వైశాల్యాలను కనుక్కోండి.
i) x – 4y + 2 = 0
సాధన:
AB సమీకరణము x – 4y + 2 = 0
– x + 4y = 2
\(\frac{x}{-2}+\frac{y}{\left(\frac{1}{2}\right)}\) = 1
a = -2, b = \(\frac{1}{2}\)
∆OAB వైశాల్యము = \(\frac{1}{2}\)|ab|
= \(\frac{1}{2}\) |-2 × \(\frac{1}{2}\)| = \(\frac{1}{2}\) చ. యూనిట్లు.

ii) 3x – 4y + 12 = 0 [A.P Mar. ’15]
సాధన:
AB సమీకరణము 3x – 4y + 12 = 0
– 3x + 4y = 12
\(\frac{x}{-4}+\frac{y}{3}\) = 1
a = – 4, b = 3
∆OAB వైశాల్యము = \(\frac{1}{2}\)|ab|
= \(\frac{1}{2}\)|(-4) (3)|= \(\frac{1}{2}\) (12)
= 6 చ. యూనిట్లు.

II.

ప్రశ్న 1.
ఒక సరళరేఖ నిరూపకాక్షాలను A, B లలో కలుస్తుంది.
i) (−5, 2) వద్ద 2 : 3 నిష్పత్తిలో \(\overline{\mathrm{A B}}\) విభజించబడినప్పుడు
సాధన:

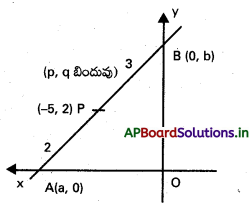
OA = a, OB = b అనుకుందాం.
A నిరూపకాలు (a, 0), B నిరూపకాలు (0, b)
P బిందువు AB ని 2 : 3 నిష్పత్తిలో విభజిస్తుంది.
P నిరూపకాలు \(\left(\frac{3 a}{5}, \frac{2 b}{5}\right)\) = (-5,2)
\(\frac{3 a}{5}\) = -5, \(\frac{3 b}{5}\) = 2
a = – \(\frac{25}{3}\), b = 5
AB సమీకరణము \(\frac{x}{a}+\frac{y}{b}\) = 1
\(\frac{x}{\left(-\frac{25}{3}\right)}+\frac{y}{5}\) = 1
\(\frac{-3 x}{25}+\frac{y}{5}\) = 1
-3x + 5y = 25
3x – 5y + 25 = 0

ii) (-5, 4) వద్ద 1:2 నిష్పత్తిలో \(\overline{\mathrm{A B}}\) ని విభజించబడినప్పుడు
సాధన:
OA = a, OB = b అనుకుందాం.
– A నిరూపకాలు (a, 0), B నిరూపకాలు (0, b)
P బిందువు AB ని 1 : 2 నిష్పత్తిలో విభజిస్తుంది.
P నిరూపకాలు \(\left(\frac{2 a}{3}, \frac{b}{3}\right)\) = (-5, 4)
\(\frac{2 a}{3}\) = -5, \(\frac{b}{3}\) = 4
a = –\(\frac{15}{2}\), b = 12
AB సమీకరణము \(\frac{x}{a}+\frac{y}{b}\) = 1
\(\frac{x}{\left(-\frac{15}{2}\right)}+\frac{y}{12}\) = 1
\(\frac{-2 x}{15}+\frac{y}{12}\) = 1
– 8x + 5y = 60
8x – 5y + 60 = 0

iii) (p, q) బిందువు \(\overline{\mathrm{A B}}\) ని సమద్విఖండన చేసినప్పుడు ఆ సరకరేఖ సమీకరణాన్ని కనుక్కోండి.
సాధన:
OA = a, OB = b అనుకుందాం.
A నిరూపకాలు (a, 0), B నిరూపకాలు (0, b)
AB మధ్యబిందువు = \(\left(\frac{a}{2}, \frac{b}{2}\right)\) = (p, q)
\(\frac{a}{2}\) = p, \(\frac{b}{2}\) = q
a = 2p, b = 2q
AB సమీకరణము \(\frac{x}{a}+\frac{y}{b}\) = 1
\(\frac{x}{2p}+\frac{y}{2q}\) = 1
\(\frac{x}{p}+\frac{y}{q}\) = 2

ప్రశ్న 2.
(−1, 2), (5, –1) బిందువుల గుండా పోయే సరళరేఖ సమీకరణం కనుక్కొని, ఈ రేఖతోను, నిరూపకాక్షాలతోను ఏర్పడే త్రిభుజ వైశాల్యాన్ని కూడా కనుక్కోండి.
సాధన:
P (-1, 2), Q (5, – 1) లు దత్త బిందువులు.
PQ సమీకరణము
(y − y₁) (x₁ − x₂) = (x − x₁) (y₁ – y₂)
(y – 2) (−1 – 5) = (x + 1) (2 + 1)
-6 (y – 2) = 3 (x + 1)
−2y + 4 = x + 1
x + 2y – 3 = 0

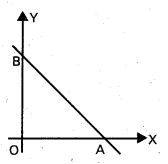
∆ OAB వైశాల్యము = \(\frac{c^2}{2|a b|}=\frac{9}{2|1.2|}=\frac{9}{4}\) చ. యూనిట్లు.

ప్రశ్న 3.
నిరూపకాక్షాలతో, ఒక సరళరేఖతోను మొదటి పాదంలో ఏర్పడిన త్రిభుజవైశాల్యం 24 చ. యూనిట్లు. ఆ సరళరేఖ (3, 4) బిందువు గుండా పోతూంటే, దాని సమీకరణం కనుక్కోండి.

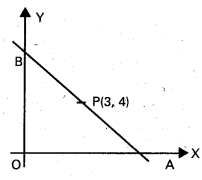
సాధన:
అంతరఖండ రూపంలో AB సమీకరణము
\(\frac{x}{a}+\frac{y}{b}\) = 1
ఈ రేఖ P (3, 4) గుండా పోతుంది.
\(\frac{3}{a}+\frac{4}{b}\) = 1
\(\frac{4}{b}=1-\frac{3}{a}=\frac{a-3}{a}\)
b = \(\frac{4 a}{a-3}\)
∆ OAB వైశాల్యము = 24 ⇒ \(\frac{1}{2}\) |ab| = 24
\(\frac{1}{2} \frac{4 a^2}{a-3}\) = 24
a² = 12 (a – 3)
= 12a – 36
a² – 12a + 36 = 0
(a – 6)² = 0 ⇒ a = 6
b = \(\frac{4 a}{a-3}=\frac{24}{3}\) = 8
AB సమీకరణము \(\frac{x}{6}+\frac{y}{8}\) = 1
4x + 3y = 24
4x + 3y – 24 = 0

ప్రశ్న 4.
వాలు 1 కలిగి Q(- 3, 5) గుండా పోయే సరళరేఖ x + y − 6 = 0 సరళరేఖను P వద్ద ఖండిస్తోంది. PQ దూరాన్ని కనుక్కోండి. [T.S Mar. ’15]

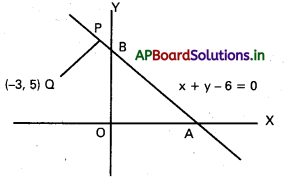
సాధన:
వాలు = 1
tan α = 1 = tan 45°
α = 45°
ఈ రేఖ Q (−3, 5) గుండా పోతుంది.
P నిరూపకాలు (x₁ + r cos α₁, y₁ + r sin α)
= (-3 + r cos 45°, 5 + r sin 45°)
= \(\left(-3+\frac{r}{\sqrt{2}}, 5+\frac{r}{\sqrt{2}}\right)\)
P బిందువు x + y − 6 = 0 రేఖపై ఉంది.
– 3 + \(\frac{r}{\sqrt{2}}\) + 5 + \(\frac{r}{\sqrt{2}}\) – 6 = 0
2 . \(\frac{r}{\sqrt{2}}\) = 4 ⇒ r = \(\frac{4 \sqrt{2}}{2}\) = 2\(\sqrt{2}\)
PQ = 2\(\sqrt{2}\)

ప్రశ్న 5.
(1, 2), (3, 4) బిందువులు 3x – 5y + a = 0 సరళరేఖకు ఒకే వైపున ఉంటే a విలువల సమితిని కనుక్కోంది.
సాధన:
P (1, 2), Q (3, 4) లు దత్త బిందువులు.
దత్తరేఖ సమీకరణము 3x – 5y + a = 0
L₁₁ = 3.1 − 5.2 + a = a − 7
L₂₂ = 3.3 – 5.4 + a = a – 11
a – 7, a – 11 లు రెండూ ధనాత్మకాలు లేదా రెండూ ఋణాత్మకాలు కావాలి.
సందర్భం (i): a – 7 > 0, a – 11 > 0
a > 7, a > 11
∴ a > 7. 11 ⇒ a ∈ (11, α)

సందర్భం (ii) : a – 7 < 0, a – 17 < 0
a < 7, a < 17
⇒ a < 17 ⇒ a = (-α, 27)
∴ a ∈ (α, 7) U (11, α)

ప్రశ్న 6.
2x + y – 3 = 0, 3x + 2y – 2 = 0, 2x – 3y – 23 = 0 సరళరేఖలు అనుషక్తాలని చూపి, అనుషక్త బిందువును కనుక్కోండి.
సాధన:
దత్త రేఖల సమీకరణాలు
2x + y – 3 = 0 ………………. (1)
3x + 2y – 2 = 0 ………………… (2)
2x – 3y – 23 = 0 …………………… (3)

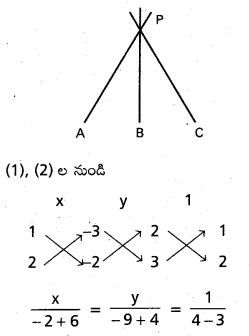
x = 4, y = -5
ఖండన బిందువు P నిరూపకాలు (4, -5)
2x – 3y – 23 = 2(4) – 3(-5) – 23
= 8 + 15 – 23 = 0
P బిందువు (3) మీద ఉంది.
దత్త రేఖలు అనుషక్తాలు.
అనుషక్త బిందువు P (4, -5)

ప్రశ్న 7.
క్రింది రేఖలు అనుపకాలయితే, ఆ విలువ కనుక్కోండి.
(i) 3x + 4y = 5, 2x + 3y = 4, px + 4y = 6
(ii) 4x – 3y – 7 = 0, 2x + py + 2 = 0, 6x + 5y – 1 = 0. [May ’06]
సాధన:
(i) దత్తరేఖల సమీకరణాలు 3x + 4y – 5 = 0
2x + 3y – 4 = 0

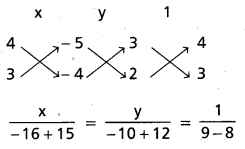
x = −1, y = 2
(1), (2) ల ఖండన బిందువు P (-1, 2)
దత్త రేఖలు అనుషక్తాలు.
P బిందువు px + 4y = 6 మీద ఉంది.
-p + 8 = 6 ⇒ p = 8 – 6 = 2

(ii) దత్తరేఖల సమీకరణాలు 4x – 3y – 7 = 0
6x + 5y – 10

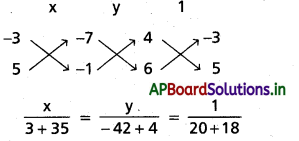
x = 1, y = -1
P నిరూపకాలు (1, −1)
దత్తరేఖలు అనుషక్తాలు.
P బిందువు 2x + py + 2 = 0 పై ఉంది.
2 – p + 2 = 0
p = 4

ప్రశ్న 8.
x + 2y – 3 = 0, 3x + 4y – 7 = 0, 2x + 3y – 4 = 0, 4x + 5y – 6 = 0 అనే నాలుగు సరళరేఖలు అనుషక్తాలు అవునో, కాదో నిర్ధారించండి.
సాధన:
దత్త రేఖల సమీకరణాలు
x + 2y – 3 = 0 …………………. (1)
3x + 4y – 7 = 0 ……………….. (2)
2x + 3y – 4 = 0 ……………….. (3)
4x + 5y – 6 = 0 ………………. (4)
(1), (2) లను సాధించగా

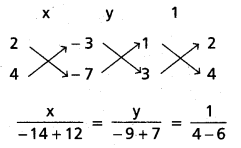
x = 1, y = 1
(1), (2) ల ఖండన బిందువు P (1, 1)
2x + 3y – 4 = 2.1 + 3.1 – 4 = 5 – 4 = 1 ≠ 0
4x + 5y – 6 = 4.1 + 5.1 – 6 = 9 – 6 = 3 ≠ 0
∴ P (1, 1) బిందువు (3), (4) ల మీద బిందువు కాదు.
∴ దత్త రేఖలు అనుషక్తాలు కావు.

ప్రశ్న 9.
3a + 2b + 4c = 0 అయితే ax + by + c = 0 సమీకరణము అనుషక్త రేఖల కుటుంబాన్ని సూచిస్తుందని చూపండి. అనుషక్త బిందువును కనుక్కోండి.
సాధన:
దత్త నియమము 3a + 2b + 4c = 0
\(\left(\frac{3}{4}\right)\)a + \(\left(\frac{1}{2}\right)\)b + c = 0
a, b ల అన్ని విలువలలో ax + by + c = 0 రేఖ
\(\left(\frac{3}{4}, \frac{1}{2}\right)\) బిందువు గుండా పోతుంది.
ax + by + c = 0 సమీకరణం అనుషక్త రేఖలను సూచిస్తుంది.
అనుషక్త బిందువు \(\left(\frac{3}{4}, \frac{1}{2}\right)\)

ప్రశ్న 10.
శూన్యేతర సంఖ్యలు a, b, c లు హరాత్మక శ్రేఢిలో ఉంటే \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) = 0 సమీకరణం ఒక అనుషక్త రేఖల కుటుంబాన్ని సూచిస్తుందని చూపి, అనుషక్త బిందువును కనుక్కోండి.
సాధన:
a, b, c లు H.P. లో వున్నాయి.
∴ \(\frac{2}{b}=\frac{1}{a}+\frac{1}{c}\)
\(\frac{1}{a}+\frac{(-2)}{b}+\frac{1}{c}\) = 0
∴ a, b, c అన్ని విలువలకు
\(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) = 0
రేఖ (1, – 2) బిందువు గుండా పోయే రేఖను సూచిస్తుంది.
∴ \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) = 0 అనుషక్త రేఖలను సూచిస్తున్నాయి.
అనుషక్త బిందువు P (1, – 2)

III.

ప్రశ్న 1.
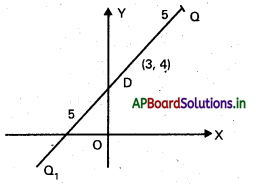
(−5, 6), (3, 2) బిందువుల నుంచి సమదూరంలో ఉంటూ, 3x + y + 4 = 0 సరళరేఖపై ఉన్న బిందువును కనుక్కోండి. [Mar. ’13]
సాధన:
P(x, y) బిందువు 3x + y + 4 = 0 మీద ఉంది.
3x + y + 4 = 0 …………….. (1)
దత్తాంశం ప్రకారం PA = PB ⇒ PA² = PB²

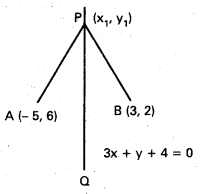
(x₁ + 5)² + (y₁ – 6)² = (x₁ – 3)² + (y₁ – 2)²
x₁² + 10x₁ + 25 + y₁² – 12y₁ + 36
= x₁² – 6x₁ + 9 + y₁² – 4y₁ + 4
16x₁ – 8y₁ +48 = 0
2x₁ – y₁ + 6 = 0 ………………. (2)
3x₁ + y₁ +4 = 0 ………………. (1)
కూడగా 5x₁ + 10 = 0 ⇒ x₁ = -2
(1) నుండి -6 + y₁ + 4 = 0
У₁ = 6 – 4 = 2
P నిరూపకాలు (-2, 2)

ప్రశ్న 2.
ఒక సరళరేఖ P (3, 4) గుండా పోతూ X – అక్షం ధన దిశతో 60° కోణం చేస్తుంది. P నుండి 5 యూనిట్ల దూరంలో ఆ రేఖపై ఉన్న బిందువులు నిరూపకాలను కనుక్కోండి.
సాధన:
రేఖ మీది ఏదేని బిందువు Q నిరూపకాలు
(x₁ + r cos θ, y₁ + r sin θ)
దత్తాంశం (x₁, y₁) = (3, 4) i.e., x₁ = 3, y₁ = 4
θ = 60° ⇒ cos = cos 60° = \(\frac{1}{2}\), sin θ = sin 60° = \(\frac{\sqrt{3}}{2}\)
సందర్భం (i) : r = 5

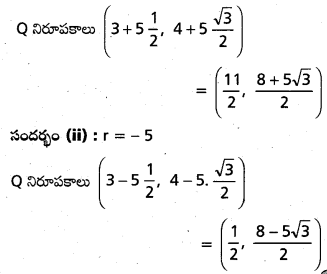
ప్రశ్న 3.
ఒక సరళరేఖ Q (\(\sqrt{3}\), 2) గుండా పోతూ, X – అక్షం ధన దిశలో \(\frac{\pi}{6}\) కోణం చేస్తుంది. ఆ సరళరేఖ \(\sqrt{3}\)x − 4y + 8 = 0 రేఖను P వద్ద ఖండిస్తూంటే PQ దూరం కనుక్కోండి. [Mar. ’04]
సూచన : AB, PQ లు లంబంగా లేవు.
కనుక మొదటి పద్ధతినుపయోగించాలి.
సాధన:

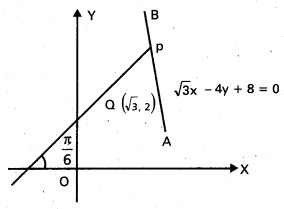
PQ రేఖ X – అక్షం ధన దిశలో \(\frac{\pi}{6}\) కోణం చేస్తుంది.
m = PQ వాలు = tan 30° = \(\frac{1}{\sqrt{3}}\)
PQ రేఖ Q (\(\sqrt{3}\), 2) గుండా పోతుంది.
PQ సమీకరణము y – 2 = \(\frac{1}{\sqrt{3}}\)(x – \(\sqrt{3}\))
\(\sqrt{3}\)y – 2\(\sqrt{3}\) = x – \(\sqrt{3}\)
x – \(\sqrt{3}\) y = – \(\sqrt{3}\) …………….. (1)
AB సమీకరణము \(\sqrt{3}\)x – 4y + 8 = 0
\(\sqrt{3}\)x – 4y = – 8 ………………. (2)
(1) × √3 = \(\sqrt{3}\)x – 3y = -3
తీసివేయగా – y = -5
y = 5
(1) నుండి x = \(\sqrt{3}\)y – \(\sqrt{3}\)
= 5\(\sqrt{3}\) – \(\sqrt{3}\) = 4\(\sqrt{3}\)
P నిరూపకాలు (4\(\sqrt{3}\), 5)
Q నిరూపకాలు (\(\sqrt{3}\), 2)
PQ² = (4\(\sqrt{3}\) – \(\sqrt{3}\))² + (5 – 2)²
27 + 9 = 36
PQ = 6 యూనిట్లు.

ప్రశ్న 4.
(2, 1), (3, – 2), (− 4, -1) బిందువులు శీర్షాలుగా గల త్రిభుజం లోపల మూలబిందువు ఉంటుందని చూపండి.
సాధన:
ABC త్రిభుజ శీర్షాలు
A (2, 1), B = (3,-2), C (-4, -1)

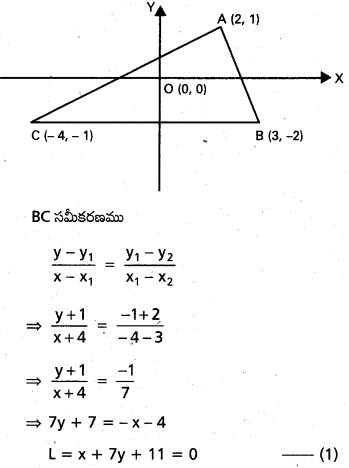
CA సమీకరణము
\(\frac{y+1}{x+4}=\frac{-1-1}{-4-2}\)
⇒ \(\frac{y+1}{x+4}=\frac{-2}{-6}\)
⇒ \(\frac{y+1}{x+4}=\frac{1}{3}\)
⇒ 3y + 3 = x + 4
⇒ L’ = x – 3y + 1 = 0 ……………….. (2)
AB సమీకరణము
\(\frac{y-1}{x-2}=\frac{1+2}{2-3}\)
⇒ \(\frac{y-1}{x-2}=\frac{3}{-1}\)
⇒ 3x – 6 = -y + 1
L” = -3x + y – 7 = 0 ………………. (3)
L” (-4, -1) = 3(-4) – 1 – 7
= – 20 ఋణాత్మకము.
L” (0, 0) = 3(0) + 0 – 7
= – 7 ఋణాత్మకము.
(- 4, -1), (0, 0) లు AB కి ఒకవైపున ఉంటాయి.
O (0, 0) – AB కి ఎడమవైపున ఉంది. ……………. (4)
L’ (3, -2) = 3 – 3 (-2) + 1
= 10 ధనాత్మకము .
L” (0, 0) = 0 – 3 (0) + 1
= 1 ధనాత్మకము
(0, 0), (3, -2) లు AC కి ఒకవైపున ఉంటాయి. …………….. (5)
L (2, 1) = 2 + 7 (1) + 11
= 20 ధనాత్మకం
L (0, 0) = 0 + 7 (0) + 11
= 11 ధనాత్మకం
(0, 0), (2, 1) లు BC కి ఒకే వైపున ఉంటాయి.
(0, 0) బిందువు BC కి ఎగువన ఉంది. …………….. (6)
(4), (5), (6) ల నుండి 0 (0,0) బిందువు AC కి దిగువన,
BC కి ఎగువన, AB కి ఎడమవైపున ఉంటుంది.
O (0, 0) బిందువు ∆ ABC లోపల ఉంటుంది.

ప్రశ్న 5.
ఒక సరళరేఖ Q(2, 3) గుండా పోతూ X – అక్షం రుణ దిశ \(\frac{3\pi}{4}\) కోణం చేస్తోంది. x + y – 7 = 0 రేఖను P వద్ద ఆ సరళరేఖ ఖండిస్తూంటే, PQ దూరాన్ని కనుక్కోండి.

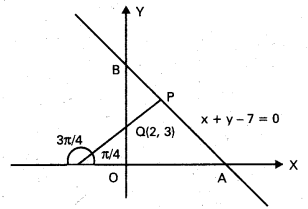
సాధన:
PQ రేఖ X – అక్షం ఋణదిశలో \(\frac{3\pi}{4}\) కోణం చేస్తుంది. PQ రేఖ X – అక్షం ధన దిశలో π – \(\frac{3\pi}{4}\) = \(\frac{\pi}{4}\) కోణం చేస్తుంది.
Q నిరూపకాలు (2, 3)
P నిరూపకాలు (x₁ + r cos θ, y₁ + r sin θ)
= (2 + r. cos \(\frac{\pi}{4}\), 3 + r . sin \(\frac{\pi}{4}\))
= \(\left(2+\frac{r}{\sqrt{2}}, 3+\frac{r}{\sqrt{2}}\right)\)
P బిందువు x + y − 7 = 0 రేఖపై ఉంది.
2 + \(\frac{r}{\sqrt{2}}\) + 3 + \(\frac{r}{\sqrt{2}}\) – 7 = 0
2 . \(\frac{r}{\sqrt{2}}\) = 7 – 2 – 3 = 2
∴ r = \(\sqrt{2}\)
PQ = r = \(\sqrt{2}\) యూనిట్లు.

ప్రశ్న 6.
x + y = 0, 3x + y – 4 = 0, x + 3y – 4 = 0 సరళరేఖలు ఒక సమబాహు త్రిభుజాన్ని ఏర్పరుస్తాయని చూపండి.
సాధన:
దత్త రేఖలు
x + y = 0 ………………… (1)
3x + y – 4 = 0 ……………….. (2)
x + 3y – 4 = 0 ………………. (3)
(1), (2) రేఖల మధ్యకోణము 8 అయితే

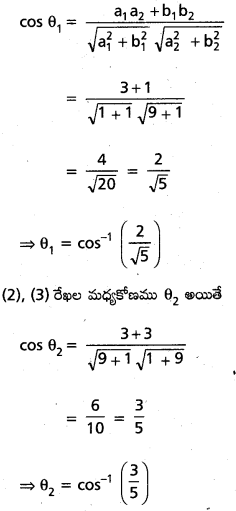
(3), (1) రేఖల మధ్యకోణము θ₃ అయితే
cos θ₃ = \(\frac{1+3}{\sqrt{1+1} \sqrt{1+9}}\)
= \(\frac{4}{\sqrt{20}}=\frac{2}{\sqrt{5}}\)
⇒ θ₃ = cos^-1 \(\left(\frac{2}{\sqrt{5}}\right)\)
θ₁ = θ₃
∴ కనుక దత్త త్రిభుజము సమద్విబాహు త్రిభుజము.

ప్రశ్న 7.
2x – y – 5 = 0, x – 5y + 11 = 0, x + y – 1 = 0 సరళరేఖలతో ఏర్పడిన త్రిభుజం వైశాల్యాన్ని కనుక్కోండి.
సాధన:
దత్త రేఖలు
2x – y – 5 = 0 ………………. (1)
x – 5y + 11 = 0 ………………. (2)
x + y – 1 = 0 ………………… (3)
(1), (2) లను సాధించగా

C నిరూపకాలు = (4, 3)
(2), (3) లను సాధించగా

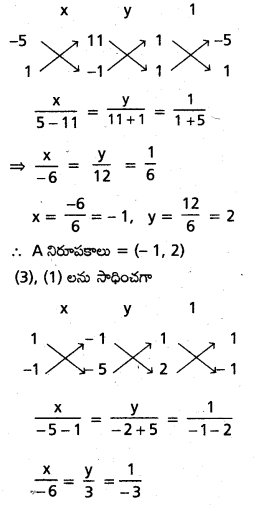
x = \(\frac{-6}{-3}\) = 2, y = \(\frac{3}{-3}\) = -1
∴ B నిరూపకాలు = (2, -1)
∆ ABC వైశాల్యం = \(\frac{1}{2}\left|\begin{array}{ll}
x_1-x_2 & x_1-x_3 \\
y_1-y_2 & y_1-y_3
\end{array}\right|\)
= \(\frac{1}{2}\left|\begin{array}{cc}
4+1 & 4-2 \\
3-2 & 3+1
\end{array}\right|\)
= \(\frac{1}{2}\left|\begin{array}{ll}
5 & 2 \\
1 & 4
\end{array}\right|\)
= \(\frac{1}{2}\) |20 – 2|
= \(\frac{1}{2}\) × 18 = 9 చ. యూనిట్లు .