AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Ex 10(d)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(d) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(d)

అభ్యాసం – 10 (డి)

I. కింద ఇచ్చిన వక్రాల మధ్యకోణం కనుక్కోండి.

ప్రశ్న 1.
x + y + 2 = 0; x² + y² – 10y = 0 (Mar. 14)
సాధన:
x + y + 2 = 0 ⇒ x = -(y + 2)
x² + y² – 10y = 0.
(y + 2)² + y² – 10y = 0
y² + 4y + 4 + y² – 10y = 0
2y² – 6y + 4 = 0
y² – 3y + 2 = 0
(y + 1) (y – 2) = 0
y = 1 లేదా= 15 y = 2
x = – (y + 2)
y = 1 ⇒ x = -(1 + 2) = -3
y = 2 ⇒ x = -(2 + 2) = -4
ఖండన బిందువులు P(-3, 1) మరియు Q(-4, 2), వక్రం సమీకరణము
x² + y² – 10y = 0
x దృష్ట్యా అవకలనము చేయగా
2x + 2y\(\frac{d y}{d x}\) – 10\(\frac{d y}{d x}\) = 0
2\(\frac{d y}{d x}\)(y – 5) = -2x
\(\frac{d y}{d x}\) = –\(\frac{x}{y-5}\)
f'(x₁) = –\(\frac{x}{y-5}\)
రేఖా సమీకరణ x + y + 2 = 0
1 + \(\frac{d y}{d x}\) = 0 ⇒ \(\frac{d y}{d x}\) = -1
g'(x₁) = -1
సందర్భం (i) :

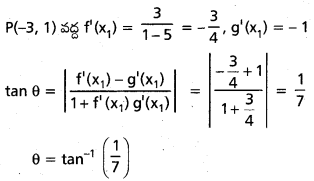
సందర్భం (ii) :
Q (-4, 2) వద్ద f'(x₁) = \(\frac{4}{2-5}\)
= –\(\frac{4}{3}\), g'(x₁) = -1

ప్రశ్న 2.
y² = 4x, x² + y² = 5
సాధన:
y ని తొలగించగా x² + 4x = 5
x² + 4x – 5 = 0
(x – 1) (x + 5) = 0
x – 1 = 0 లేదా -5
y² = 4x
x = 1 లేదా – 5
y² = 4x
x = 1 ⇒ y² = 4
y = ±2
x = -5 ⇒ y వాస్తవం కాదు
∴ ఖండన బిందువులు (1, 2) మరియు Q(1, -2) మొదటి వక్రం సమీకరణము y² = 4x
2y. \(\frac{d y}{d x}\) = 4
\(\frac{d y}{d x}\) = \(\frac{4}{2 y}\)
f'(x) = \(\frac{2}{y}\)
రెండవ వక్రం సమీకరణం x² + y² = 5
2x + 2y \(\frac{d y}{d x}\) = 0
2y. \(\frac{d y}{d x}\) = -2x
\(\frac{d y}{d x}\) = \(-\frac{2 x}{2 y}\) = –\(\frac{x}{y}\) ; g'(x) = \(-\frac{x}{y}\)
P(1, 2) వద్ద f'(x₁) = \(\frac{2}{2}\) = 1, g'(x₁) = –\(\frac{1}{2}\)

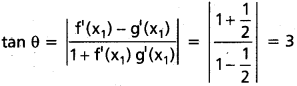
θ = tan^-1 (3)
Q(1, -2) వద్ద f'(x₁) = \(\frac{2}{-2}\) = -1, g'(x₁) = \(\frac{1}{2}\)

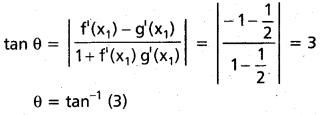
ప్రశ్న 3.
x² + 3y = 3, x² – y² + 25 = 0
సాధన:
x² = 3 – 3y ; x² – y² + 25 = 0
3 – 3y – y² + 25 = 0
y² – 3y – 28 = 0
(y – 4) (y + 7) = 0
y – 4 = 0 (లేదా) y + 7 = 0
y = 4 లేదా -7
x² = 3 – 3y
y = 4 ⇒ x² = 3 – 12 = -9 ⇒ x వాస్తవం కాదు
y = -7 ⇒ x² = 3 + 21 = 24
⇒ x = ± \(\sqrt{24}\) = ±2\(\sqrt{6}\)
ఖండన బిందువు P(\(2 \sqrt{6}\), 7), Q(\(-2 \sqrt{6}\), -7)
మొదటి వక్రం సమీకరణము x² + 3y = 3
3y = 3 – x²
3 \(\frac{d y}{d x}\) = -2x
\(\frac{d y}{d x}\) = \(-\frac{2 x}{3}\) i.e., f'(x₁) = \(-\frac{2 x}{3}\)
రెండవ వక్రం సమీకరణము
x² – y² + 25 = 0
y² = x² + 25

ప్రశ్న 4.
x² = 2(y + 1); y = \(\frac{8}{x^2+4}\)
సాధన:
x² = 2\(\left(\frac{8}{x^2+4}+1\right)\) = \(\frac{16+2 x^2+8}{x^2+4}\)
x²(x² + 4) = 2x² + 24
x⁴ + 4x² – 2x² – 24 = 0
x⁴ + 2x² – 24 = 0
(x² + 6) (x² – 4) = 0
x² = -6 లేదా x² = 4
x² = -6 ⇒ x = ±2
y = \(\frac{8}{x^2+4}\) = \(\frac{8}{4+4}\) = \(\frac{8}{8}\) = 1
∴ ఖండన బిందువులు P(2, 1) మరియు Q(-2, 1)
మొదటి వక్రం సమీకరణం x,sup>2 = 2(y + 1)
2x = 2. \(\frac{d y}{d x}\) ⇒ \(\frac{d y}{d x}\) = x
f'(x₁) = x₁
రెండవ వక్రం సమీకరణము y = \(\frac{8}{x^2+4}\)
\(\frac{d y}{d x}\) = \(\frac{8(-1)}{\left(x^2+4\right)^2}\) 2x = –\(\frac{16 x}{\left(x^2+4\right)^2}\)
g'(x₁) = –\(\frac{16 x}{\left(x^2+4\right)^2}\)
P(2, 1) వద్ద f'(x₁) = 2.
g'(x₁) = \(\frac{-16 \times 2}{8^2}\) = \(-\frac{32}{64}\) = \(-\frac{1}{2}\)
f'(x₁). g’ (x₁) = 2 × (\(-\frac{1}{2}\)) = -1
∴ దత్త వక్రాలు లంబంగా ఖండించుకుంటున్నాయి.
i.e., θ = \(\frac{\pi}{2}\)

ప్రశ్న 5.
2y² – 9x = 0; 3x² + 4y = 0 (4వ పాదంలో)
సాధన:
2y² – 9x = 0 ⇒ 9x = 2y²
x = \(\frac{2}{9} y^2\)
3x² + 4y = 0 ⇒ 3.\(\frac{4}{81}\)y⁴ + 4y = 0
\(\frac{4 y^4+108 y}{27}\) = 0
4y(y³ + 27) = 0
y = 0 లేదా y³ = -27 ⇒ y= -3.
9x = 2y² = 2 × 9 ⇒ x = 2
ఖండన బిందువులు (4 వ పాదంలో) P(2, -3)
మొదటి వక్రం సమీకరణము 2y² = 9x
4y\(\frac{d y}{d x}\) = 9 ⇒ \(\frac{d y}{d x}\) = \(\frac{9}{4 y}\)
f'(x) = \(\frac{9}{4 y}\)
P(2,-3) వద్ద f'(x) = \(\frac{9}{-12}\) = \(-\frac{3}{4}\)
రెండవ వక్రం సమీకరణము
3x² + 4y = 0
4y = -3x²
4. \(\frac{d y}{d x}\) = -6x
\(\frac{d y}{d x}\) = \(\frac{-6 x}{4}\) = \(\frac{-3 x}{2}\)
P(2,-3) వద్ద g'(x₁) = \(\frac{-6}{2}\) = -3

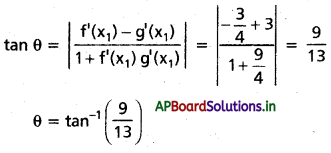
ప్రశ్న 6.
y² = 8x, 4x² + y² = 32
సాధన:
4x² + 8x = 32 ⇒ x² + 2x = 8
x² + 2x – 8 = 0
(x – 2) (x + 4) = 0
x = 2 లేదా -4
y² = 8x
x = -4 → y² వాస్తవం కాదు
x = 2 ⇒ y² = 16 ⇒ y = ±4
ఖండన బిందువులు P(2, 4), Q(2, – 4)
మొదటి వక్రం సమీకరణము y² = 8x
2y. \(\frac{d y}{d x}\) = 8 ⇒ \(\frac{d y}{d x}\) = \(\frac{8}{2 y}\) = \(\frac{4}{y}\)
f'(x₁) = \(\frac{4}{y}\)
రెండవ వక్రం సమీకరణము
4x₂ + y₂ = 32
8x + 2y. \(\frac{d y}{d x}\) = 0
2y\(\frac{d y}{d x}\) = -8x ⇒ \(\frac{d y}{d x}\) = \(\frac{-8 x}{2 y}\) = \(\frac{-4 x}{y}\)
g'(x₁) = \(-\frac{4 x}{y}\)
P(2, 4) వద్ద f'(x₁) = \(\frac{4}{4}\) = 1,
g'(x₁) = \(\frac{-4.2}{4}\) = -2
tan θ = |\(\frac{f^{\prime}\left(x_1\right)-g^{\prime}\left(x_1\right)}{1+f^{\prime}\left(x_1\right) g^{\prime}\left(x_1\right)}\)| = |\(\frac{1+2}{1-2}\)| = 3
θ = tan^-1(3)
Q(2, -4) వద్ద f'(x₁) = \(\frac{4}{-4}\) = -1,
g'(x₁) = \(\frac{-4.2}{-4}\) = 2
tan θ = |\(\frac{f^{\prime}\left(x_1\right)-g^{\prime}\left(x_1\right)}{1+f^{\prime}\left(x_1\right) g^{\prime}\left(x_1\right)}\)| = |\(\frac{-1-2}{1+(-1) \cdot 2}\)|
= |\(\frac{-3}{-1}\)| = 3
θ = tan^-1(3)

ప్రశ్న 7.
x₂y = 4; y(x₁ + 4) = 8.
సాధన:
x₂y = 4 ⇒ x² = \(\frac{4}{y}\)
y(x₂ + 4) = 8
y\(\frac{(4+4 y)}{y}\) = 8
\(y \frac{(4+4 y)}{y}\) = 8
4y – 4 ⇒ y = 1
x₂ = 4 ⇒ x₂ = ±2
ఖండన బిందువులు P (2, 1), Q (-2, 1)
x₂y = 4 ⇒ y = \(\frac{4}{x^2}\)

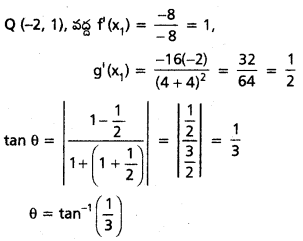
ప్రశ్న 8.
6x₂ – 5x + 2y = 0, 4x₂ + 8y₂ = 3 విక్రాలు (\(\frac{1}{2}\), \(\frac{1}{2}\)) బిందువు వద్ద స్పృశించుకొంటాయని చూపండి. (A.P Mar. ’15)
సాధన:
మొదటి వక్రం సమీకరణము
6x₂ – 5x + 2y = 0
2y = 5x – 6x₂
2. \(\frac{d y}{d x}\) = 5 – 12x
\(\frac{d y}{d x}\) = \(\frac{5-12 x}{2}\)
P(\(\frac{1}{2}\), \(\frac{1}{2}\)) వద్ద f'(x₁) = \(\frac{5-12 \cdot \frac{1}{2}}{2}\)
= \(\frac{5-6}{2}\) = \(-\frac{1}{2}\)
రెండవ వక్రం సమీకరణము 4x² + 8y² = 3
8x + 16y. \(\frac{d y}{d x}\) = 0
16y. \(\frac{d y}{d x}\) = -8x
\(\frac{d y}{d x}\) = \(\frac{-8 x}{16 y}\) = \(-\frac{x}{2 y}\)
P(\(\frac{1}{2}\), \(\frac{1}{2}\)) వద్ద g'(x₁) = \(\frac{-\frac{1}{2}}{2\left(\frac{1}{2}\right)}\) = \(-\frac{1}{2}\)
∴ f'(x₁) = g'(x₁)
దత్త వక్రాలు P(\(\frac{1}{2}\), \(\frac{1}{2}\)) వద్ద స్పృశించుకొంటాయి.