AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Ex 3(e)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 3 సరళరేఖ Exercise 3(e) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Exercise 3(e)

అభ్యాసం – 3 (ఇ)

I.

ప్రశ్న 1.
(1, \(\sqrt{3}\) ) (2, 0), (0, 0) లు శీర్షాలుగా గల త్రిభుజం అంతర కేంద్రం కనుక్కోండి.
సాధన:
O(0, 0), A (1, \(\sqrt{3}\)), B (2, 0) లు ∆ ABC శీర్షాలు

ప్రశ్న 2.
x + y + 10 = 0, x – y − 2 = 0, 2x + y +7 = 0 భుజాలుగా గల త్రిభుజ లంబకేంద్రం కనుక్కోండి. [May ’13]
సాధన:
AB సమీకరణము x + y + 10 = 0 …………….. (1)
BC సమీకరణము x – y – 2 = 0 ………………… (2)
AC సమీకరణము 2x + y – 7 = 0 ……………… (3)

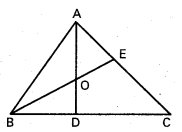
(1), (2) లను సాధించగా B నిరూపకాలు (-4, -6)
(1), (3) లను సాధించగా A నిరూపకాలు (17, 27)
BC సమీకరణము x – y – 2 = 0
AD రేఖ BC కి లంబంగా ఉంది.
AD సమీకరణము x + y + k = 0
AD రేఖ A (17, −27) గుండా పోతుంది.
17 – 27 + k = 0 ⇒ k = 10
∴ AB సమీకరణము x + y + 10 = 0 ……………. (1)
AC సమీకరణము 2x + y – 7 = 0
BE రేఖ AC కి లంబంగా ఉంది.
DE సమీకరణము x – 2y = k
BE సమీకరణము B (-4, -6)
-4 + 12k = k ⇒ k = 8
BE సమీకరణము x – 2y = 8

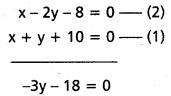
3y = -18 ⇒ y = -6
x + y + 10 = 0 ⇒ x – 6 + 10 = 0
x = 6 – 10 = -4
∆ ABC యొక్క లంబకేంద్రం (-4, – 6)

ప్రశ్న 3.
4x – 7y + 10 = 0, x + y = 5, 7x + 4y = 15 భుజాలుగా గల త్రిభుజ లంబకేంద్రం కనుక్కోండి.
సాధన:
AB సమీకరణము 4x – 7y + 10 = 0 ……………. (1)
BC సమీకరణము x + y = 5 ………………… (2)
AC సమీకరణము 7x + 4y – 15 = 0 ………………. (3)
AB, AC లు లంబంగా ఉన్నాయి. ∠A = 90°
∴ ABC లంబకోణ త్రిభుజం
లంబకోణ శీర్షం A లంబకేంద్రం
(1), (3) లను సాధించగా

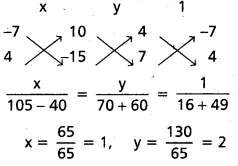
లంబకేంద్రం O (1, 2)

ప్రశ్న 4.
x = 1, y = 1, x + y = 1 భుజాలుగా గల త్రిభుజ పరికేంద్రం కనుక్కోండి.
సాధన:
AB సమీకరణము x = 1
BC సమీకరణము y = 1
AC సమీకరణము x + y = 1

AB, BC లు లంబాలు
∴ ABC ఒక లంకోణ త్రిభుజము ∠B = 90°
AC మధ్య బిందువు, AC పరికేంద్రము
A నిరూపకాలు (1, 0), C నిరూపకాలు (0, 1).
పరికేంద్రము \(\left(\frac{1}{2}, \frac{1}{2}\right)\)

ప్రశ్న 5.
x = 1, y = 1, x + y = 1 లు భుజాలుగా గల త్రిభుజం అంతర కేంద్రం కనుక్కోండి.
సాధన:
AB సమీకరణము X = 1
BC సమీకరణము y = 1
AC సమీకరణము x + y = 1
సాధించగా A(1, 0), B (1, 1), C (0, 1) లు శీర్షాలు

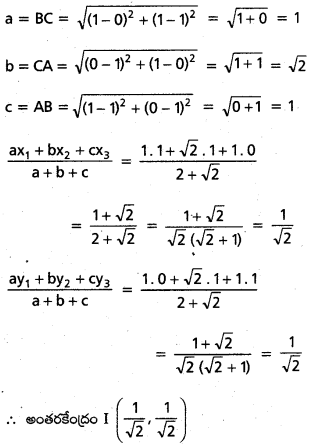
ప్రశ్న 6.
(1, 0),(–1, 2), (3, 2) శీర్షాలుగా గల త్రిభుజం పరికేంద్రం కనుక్కోండి.
సాధన:
A (1, 0), B (-1, 2), C (3, 2) లు ∆ ABC త్రిభుజ శీర్షాలు

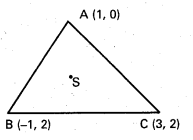
S (x, y) ∆ ABC యొక్క పరికేంద్రం
SA = SB = SC
SA = SB ⇒ SA² = SB²
(x – 1)² + y² = (x + 1)² + (y – 2)²
x² – 2x + 1 + y² = x² + 2x + 1 + y² – 4y + 4
4x – 4y = -4 ⇒ x – y = -1 ………………. (1)
SB SC ⇒ SB² = SC²
(x + 1)² + (y – 2)² = (x – 3) + (y – 2)²
x² + 2x + 1 = x² – 6x + 9
8x = 8 ⇒ x = 1
(1) నుండి 1 – y = -1
y = 2
∴ పరికేంద్రము (1, 2)

ప్రశ్న 7.
kx + y + 9 = 0, 3x – y = 4 సరళరేఖల మధ్యకోణం 45° అయితే k విలువను కనుక్కోండి.
సాధన:
దత్త రేఖల సమీకరణాలు
kx + y + 9 = 0
3x – y + 4 = 0
cos \(\frac{\pi}{4}\) = \(\frac{|3 k-1|}{\sqrt{k^2+1} \sqrt{9+1}}\)
\(\frac{1}{\sqrt{2}}=\frac{|3 k-1|}{\sqrt{10} \sqrt{k^2+1}}\)
వర్గీకరించి అడ్డగుణకారము చేయగా
5k² + 5 = (3k – 1)² = 9k² – 6k + 1
4k² – 6k – 4 = 0
2k² – 3k – 2 = 0
(k – 2) (2k + 1) = 0
k = 2 లేదా -1/2

ప్రశ్న 8.
మూల బిందువు గుండాను 2x + y + 5 = 0, x + y + 1 = 0 సరళ రేఖల ఖండన బిందువు గుండాను పోయే సరళరేఖ సమీకరణం కనుక్కోండి.

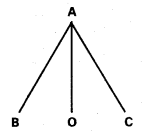
సాధన:
AB సమీకరణము L₁ = 2x – y + 5 = 0
AC సమీకరణము L₂ = x + y + 1 = 0
A గుండా పోయే ఏదేని రేఖ సమీకరణము
L₁ + KL₂ = 0
(2x – y + 5) +k (x + y + 1) = 0 ……………… (1)
ఈ రేఖ 0 (0, 0) ల గుండా పోతుంది.
5 + k = 0 ⇒ k = -5
(1) నుండి ప్రతిక్షేపించగా OA సమీకరణం
(2x + y + 5) − 5(x + y + 1) = 0
2x – y + 5 – 5x – 5y – 5 = 0
-3x – 6y = 0 ⇒ x + 2y = 0

ప్రశ్న 9.
3x + 4y,= 7 రేఖకు సమాంతరంగా ఉంటూ, x – 2y – 3 = x + 3y – 6 = 0 సరళరేఖల ఖండన బిందువు గుండా పోయే సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
దత్త రేఖల సమీకరణాలు
L₁ = x – 2y – 3 = 0 మరియు
L₂ = x + 3y – 6 = 0
ఖండన బిందువు గుండా పోయే ఏదేని రేఖ సమీకరణము
L₁ + kL₂ = 0
(x – 2y – 3) + k(x + 3y – 6) = 0
(1 + k)x + (-2 + 3k)y + (-3 – 6k) = 0
ఈ రేఖ 3x + 4y = 7 కు సమాంతరం.
a₁b₂ = a₂b₁
3(−2 + 3k) = (1 + k) 4
– 6 + 9k = 4 + 4k
⇒ 5k = 10 ⇒ k = 2 +
కావలసిన రేఖ సమీకరణం 3x + 4y – 15 = 0

ప్రశ్న 10.
2x + 3y = 0 రేఖకు లంబంగా ఉంటూ x + 3y – 1 = 0, x − 2y + 4 = 0 రేఖల ఖండన బిందువు గుండా పోయే సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
AB సమీకరణము x + 3y – 1 = 0
AC సమీకరణము X -2y + 4 = 0

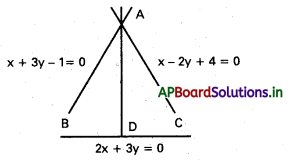
A గుండా పోయే ఏదేని రేఖ సమీకరణము
(x + 3y – 1) + k(x – 2y + 4) = 0
(1 + k)x + (3 – 2k)y + (4k – 1) = 0 ……………… (1)
ఈ రేఖ 2x + 3y = 0 కు లంబము
a₁a₂ + b₁b₂ = 0
2(1 + k) + 3(3 – 2k) = 0
2 + 2k + 9 – 6k = 0
4k = 11 ⇒ k = \(\frac{11}{4}\)
(1) లో ప్రతిక్షేపిస్తే AD సమీకరణము
\(\left(1+\frac{11}{4}\right)\) x + \(\left(3-\frac{11}{2}\right)\) y + (11 – 1) = 0
\(\frac{15}{4}\) x – \(\frac{5}{2}\) y + 10 = 0
15x – 10y + 40 = 0
3x – 2y + 8 = 0

ప్రశ్న 11.
నిరూపకాక్షాలతో శూన్యేతర సమాన అంతర ఖండాలు చేస్తూ, 2x – 5y + 1 = 0, x – 3y – 4 = 0 సరళరేఖల ఖండన బిందువు గుండా పోయే సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
దత్త రేఖల సమీకరణాలు
L₁ = 2x – 5y + 1 = 0
L₂ = x – 3y – 4 = 0
ఈ రేఖల ఖండన బిందువు గుండా పోతే
ఏదేని రేఖ సమీకరణము
L₁ + kL₂ = 0
(2x – 5y + 1) + k(x – 3y – 4) = 0
(2 + k)x – (5+ 3k)y + (1 – 4k) = 0 …………….. (1)
అంతర ఖండాలు సమానం
2 + k – 5 – 3k
4k = -7
⇒ k = -7/4
(1) లో ప్రతిక్షేపించగా కావలసిన రేఖ సమీకరణము
\(\left(2-\frac{7}{4}\right)\) x – \(\left(5-\frac{21}{4}\right)\) y + (1 + 7) = 0
\(\frac{1}{4}\)x + \(\frac{1}{4}\)y + 8 = 0
⇒ x + y + 32 = 0

ప్రశ్న 12.
3x + 2y + 4 = 0, 2x + 5y − 1 = 0, రేఖల ఖండన బిందువు నుంచి 7x + 24y – 15 0 సరళరేఖకు గల లంబదూరం కనుక్కోండి.
సాధన:
దత్త రేఖల సమీకరణాలు
3x + 2y + 4 = 0
2x + 5y – 1 = 0

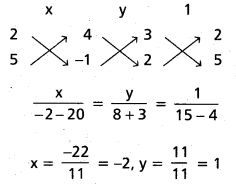
P నిరూపకాలు (-2, 1)
రేఖ సమీకరణము 7x + 24y – 15 = 0
లంబ దూరము
= \(\left|\frac{-14+24-15}{\sqrt{49+576}}\right|=\frac{5}{25}=\frac{1}{5}\)

ప్రశ్న 13.
3x + 4y – 8 = 0 సరళరేఖల నుంచి (2, 3), (-4, a) బిందువుల దూరాలు సమానమయితే ‘a’ విలువ కనుక్కోండి.
సాధన:
PQ సమీకరణము 3x + 4y – 8 – 0
P (2, 3), Q (-4, a) లు దత్త బిందువులు.
PP’, QQ’ లు P, ల నుండి లంబం

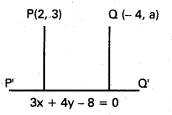
PP’ = QQ’
\(\frac{|3.2+4.3-8|}{\sqrt{9+16}}=\frac{|3 \cdot(-4)+4 a-8|}{\sqrt{9+16}}\)
10 = |4a – 20|
4a – 20 = ±10 ⇒ 4a = 20 ± 10 = 30 లేదా 10
a = \(\frac{30}{4}\) లేదా \(\frac{10}{4}\)
i.e., a = \(\frac{15}{2}\) లేదా 5/2

ప్రశ్న 14.
x + y = 0, 2x + y + 5 = 0, x – y = 2 భుజాలుగా గల త్రిభుజ పరికేంద్రం కనుక్కోండి.
సాధన:
AB సమీకరణము x + y = 0 ………………. (1)
BC సమీకరణము 2x + y + 5 = 0 ……………… (2)
AC సమీకరణము x – y = 2 ……………. (3)

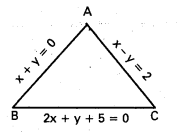
(1), (2) లను సాధిస్తే, B నిరూపకాలు (-5, 5)
(2), (3) లను సాధిస్తే, A నిరూపకాలు (-1,-3)
(1), (3) సాధిస్తే A నిరూపకాలు (1, -1)
S(x, y) పరికేంద్రం అనుకుందాం.
SA = SB = SC
SA = SB ⇒ SA² = SB²
(x + 5)² + (y − 5)² = (x + 1)² + (y + 3)²
x² + 10x + 25 + y² – 10y + 25
= x² + 2x + 1 + y² + 6y + 9
8x – 16y = -40
x – 2y = -5 ………………. (1)
SB = SC ⇒ SB² = SC²
(x + 1)² + (y + 3)² = (x – 1)² + (y + 1)²
x² + 2x + 1 + y² + 6y + 9
x² – 2x + 1 + y² + 2y + 1
4x + 4y = -8
x + y = -2 …………… (2)
(2) – (1) 3y = 3 ⇒ y = 1
x + 1 = -2 ⇒ x = -3
పరికేంద్ము S(-3, 1)

ప్రశ్న 15.
\(\frac{x}{a}+\frac{y}{b}\) = 1, \(\frac{x}{b}+\frac{y}{a}\) = 1 రేఖల మధ్య కోణం θ అయితే a > b అయినప్పుడు sin θ విలువ కనుక్కోండి.
సాధన:
AB సమీకరణము \(\frac{x}{a}+\frac{y}{b}\) = 1 ⇒ bx + ay = ab
AC సమీకరణము \(\frac{x}{b}+\frac{y}{a}\) = 1 ⇒ bx + ay = ab

II.

ప్రశ్న 1.
(−10, 4) బిందువు గుండా పోతూ x – 2y = 10 రేఖతో θ కోణాన్ని tan θ = 2 అయ్యేటట్లు చేసే సరళరేఖల సమీకరణాలు కనుక్కోండి:
సాధన:
QR సమీకరణము x – 2y = 10

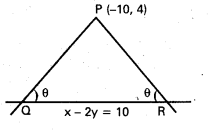
PQ వాలు m అనుకుందాం.
PQ రేఖ P(-10, 4) గుండా పోతుంది.
PQ సమీకరణము y – 4 = m(x + 10) У
= mx + 10m …………….. (1)
i.e., mxy + (10m + 4) = 0
tan θ = 2 ⇒ cos θ = \(\frac{1}{\sqrt{5}}\)
cos θ = \(\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\)
\(\frac{1}{\sqrt{5}}=\frac{|m+2|}{\sqrt{1+4} \sqrt{m^2+1}}\)
వర్గీకరించి, అడ్డగుణకారము చేయగా
m² + 1 = (m + 2)²
= m² + 4m + 4
4m + 3 = 0
m = –\(\frac{3}{4}\)

సందర్భం (i) : m² = 0
⇒ ఒక మూలము ∞
PR ఊర్ధ్వ రేఖ
∴ PR సమీకరణము x + 10 = 0

సందర్భం (ii) : m = –\(\frac{3}{4}\)
(1) లో ప్రతిక్షేపించగా
PQ సమీకరణము –\(\frac{3}{4}\) x – y + \(\left(-\frac{30}{4}+4\right)\) = 0
\(\frac{-3 x-4 y-14}{4}\) = 0
⇒ 3x + 4y + 14 = 0

ప్రశ్న 2.
(1, 2) బిందువు గుండా పోతూ \(\sqrt{3}\) x + y + 2 = సరళరేఖతో 60° కోణాన్ని చేసే సరళరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
QR సమీకరణము \(\sqrt{3}\)x + y + 2 = 0

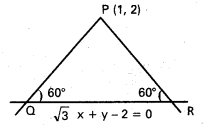
PQ, PR లు P(1, 2) గుండా పోతూ QR తో 60° కోణం చేస్తున్నాయి.
PQ వాలు m అనుకుందాం.
PQ వాలు у – 2 = m(x − 1)
= mx – m
mx – y + (2 – m) = 0 ………………. (1)
cos θ = \(\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\)
cos 60° = \(\frac{|\sqrt{3} m-1|}{\sqrt{3+1} \sqrt{m^2+1}}\)
\(\frac{1}{2}\) = \(\frac{|\sqrt{3} m-1|}{2 \sqrt{m^2+1}}\)
వర్గీకరించి అడ్డగుణకారము చేయగా
m² + 1 = (\(\sqrt{3}\)m – 1)²
= 3m² + 1 – 2\(\sqrt{3}\) m
2m² – 2\(\sqrt{3}\) m = 0
2m(m – \(\sqrt{3}\)) = 0
m = 0 లేదా \(\sqrt{3}\)
సందర్భం (i) : m = 0
PQ సమీకరణము -y + 2 = 0 లేదా y – 2 = 0
సందర్భం (ii) : m = \(\sqrt{3}\)
PQ సమీకరణము \(\sqrt{3}\)x – y + (2 – \(\sqrt{3}\)) = 0

ప్రశ్న 3.
ఒక సమబాహు త్రిభుజం భూమి x + y – 2 = 0, ఎదుటి శీర్షం (2, −1) అయితే మిగిలిన భుజాల సమీకరణాలు కనుక్కోండి.
సాధన:
ABC సమబాహు త్రిభుజము
∴ ∠B = ∠C = 60°

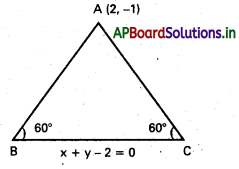
BC సమీకరణము x + y – 2 = 0
AB రేఖ A(2, -1) గుండా పోతుంది.
AB వాలు = m అనుకుందాం.
AB సమీకరణము y + 1 = m(x – 2)
= mx – 2m
mx – y – (2m + 1) = 0 ………………. (1)
cos 60° = \(\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\)
\(\frac{1}{2}\) = \(\frac{|m-1|}{\sqrt{1+1} \sqrt{m^2+1}}\)
వర్గీకరించి, అడ్డగుణకారము చేయగా,
m² + 1 = 2 (m − 1)² = 2 (m² – 2m + 1)
= 2m² – 4m + 2
m² – 4m + 1 = 0
m = \(\frac{4 \pm \sqrt{16-4}}{2}\) = \(\frac{4 \pm 2 \sqrt{3}}{2}\) = 2 ± \(\sqrt{3}\)
(1) లో ప్రతిక్షేపిస్తే,
AB సమీకరణము y + 1 = (2 + \(\sqrt{3}\)) (x – 2)
AC సమీకరణము y + 1 = (2\(\sqrt{3}\)) (x – 2)

ప్రశ్న 4.
కింద సూచించిన శీర్షాలు గల త్రిభుజం లంబకేంద్రాన్ని కనుక్కోండి. [A.P. Mar. ’15, ’12, ’07, ’04]
i) (-2, -1), (6, -1), (2, 5)
ii) (5,-2), (-1, 2), (1, 4)
సాధన:
i) A(-2, -1), B(6, -1), C(2, 5) ∆ ABC లు త్రిభుజ శీర్షాలు

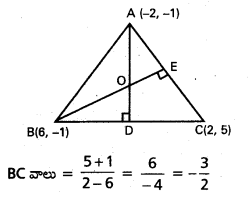
AD కి BC లు లంబంగా ఉంది.
AD వాలు = \(\frac{2}{3}\)
AD సమీకరణము
y + 1 = \(\frac{2}{3}\) (x + 2)
2x – 3y + 1 = 0 ………………. (1)
AC వాలు = \(\frac{5+1}{2+2}=\frac{6}{4}=\frac{3}{2}\)
BE కి AC లు లంబంగా ఉంది.
BE వాలు = –\(\frac{2}{3}\)
BE సమీకరణము
y + 1 = –\(\frac{2}{3}\) (x – 6)
2x + 3y – 9 = 0 ………………… (2)

ii) (5,-2), (1, 2), (1, 4)
A(5,-2), B(-1, 2), C(1, 4) ∆ ABC లు త్రిభుజ శీర్షాలు
BC వాలు = \(\frac{2-4}{-1-1}=\frac{-2}{-2}\) = 1
AD రేఖ BC కి లంబంగా ఉంది.

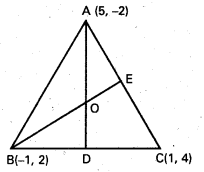
AD వాలు = –\(\frac{1}{m}\) = -1
AD సమీకరణము y + 2 = -(x – 5)
= -x + 5
x + y – 3 = 0 ………………. (1)
BE రేఖ AC’కి లంబంగా ఉంది.
BE వాలు = –\(\frac{1}{m}\) = \(\frac{2}{3}\)
BE సమీకరణము y – 2 = 1 (x + 1)
3y – 6 = 2x + 2
2x – 3y + 8 = 0 ………………… (2)
(1), (2) ల నుండి అడ్డగుణకార సూత్రం ప్రకారం

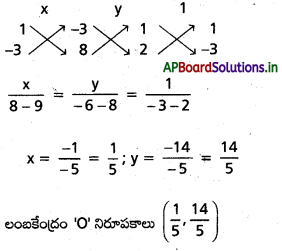
ప్రశ్న 5.
కింద ఇచ్చిన శీర్షాలు గల త్రిభుజం పరికేంద్రం కనుక్కోండి.
i) (-2, 3) (2, -1), (4, 0) [Mar. ’11]
ii) (1, 3), (0, -2), (-3, 1) [May ’06]
సాధన:
i) A(-2, 3), B(2, −1), C(4, 0) ∆ ABC లు శీర్షాలు
BC మధ్య బిందువు D

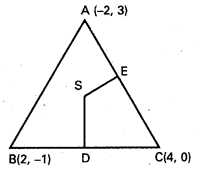
D నిరూపకాలు \(\left(\frac{2+4}{2}, \frac{-1+0}{2}\right)\)
= \(\left(3, \frac{-1}{2}\right)\)
BC వాలు = \(\frac{-1-0}{2-4}=\frac{-1}{-2}=\frac{1}{2}\)
SD రేఖ BC కి లంబంగా ఉంది.
SD వాలు = –\(\frac{1}{m}\) = -2
SD సమీకరణము y + \(\frac{1}{2}\) = -2(x – 3)
2y + 1 = -4(x – 3)
= – 4x + 12
4x + 2y – 11 = 0 ………………. (1)
AC కి మధ్య బిందువు E
E నిరూపకాలు \(\left(\frac{-2+4}{2}, \frac{3+0}{2}\right)=\left(1, \frac{3}{2}\right)\)
AC వాలు = \(\frac{3-0}{-2-4}=-\frac{3}{6}=-\frac{1}{2}\)
SE రేఖ AC కి లంబంగా ఉంది.
SE వాలు = –\(\frac{1}{m}\) = 2
SE సమీకరణము y – \(\frac{3}{2}\) = 2(x – 1)
2y – 3 = 4(x – 1)
= 4x – 4
4x – 2y – 1 = 0 ……………….. (2)
4x + 2y – 11 = 0 …………….. (1)
(1), (2) ల నుండి ⇒ 8x – 12 = 0
8x = 12
x = \(\frac{12}{8}\) = \(\frac{3}{2}\)
(1) లో ప్రతిక్షేపించగా
2y = 11 – 4x = 11 – 4 . \(\frac{3}{2}\) = 11 – 6 = 5
y = \(\frac{5}{2}\)
∴ S నిరూపకాలు \(\left(\frac{3}{2}, \frac{5}{2}\right)\)

ii) (1, 3), (0, −2) మరియు (−3, 1)

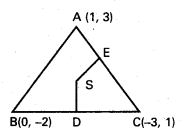
లో ∆ ABC,
A = (1, 3), B = (0,-2), C = (-3, 1)
D మధ్య బిందువు BC
D = \(\left(\frac{0-3}{2}, \frac{-2+1}{2}\right)=\left(\frac{-3}{2}, \frac{-1}{2}\right)\)
BC వాలు = \(\frac{1+2}{-3-0}\) = -1
SD రేఖ BC కి లంబం.
SD వాలు = 1
SD సమీకరణము
y + \(\frac{1}{2}\) = 1(x + \(\frac{3}{2}\))
⇒ 2y + 1 = 2x + 3
⇒2x – 2y + 2 = 0
⇒x – y + 1 = 0
CA కి మధ్య బిందువు E
⇒ E = \(\left(\frac{-3+1}{2}, \frac{1+3}{2}\right)\) = (-1, 2)
CA వాలు = \(\frac{1-3}{-3-1}=\frac{1}{2}\)
SE రేఖ CA కి లంబం.
SE వాలు = -2
SE సమీకరణము
y – 2 = -2(x + 1)
⇒ y – 2 = 2x – 2
⇒ 2x + y = 0 ……………… (2)
(1), (2) లను సాధించగా

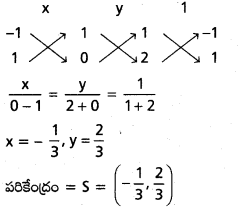
ప్రశ్న 6.
P(2, 2), Q (6, – 1), R(7, 3) శీర్షాలుగా గల త్రిభుజానిక \(\overleftrightarrow{\mathrm{P S}}\) మధ్యగతం అయితే (1, -1) గుండా పోతూ \(\overleftrightarrow{\mathrm{P S}}\) మధ్యగత రేఖకు సమాంతరంగా ఉండే సరళరేఖ సమీకరణం కనుక్కోండి.

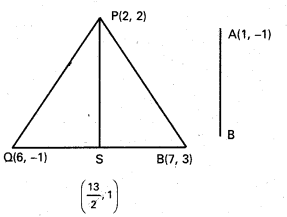
సాధన:
P(2, 2), Q(6, -1), R(7, 3) లు ∆ABC శీర్షాలు
S మధ్య బిందువు QR
S నిరూపకాలు \(\left(\frac{6+7}{2}, \frac{-1+3}{2}\right)=\left(\frac{13}{2}, 1\right)\)
PS వాలు = \(\frac{1-2}{\frac{13}{2}-2}=-\frac{1}{\left(\frac{9}{2}\right)}=-\frac{2}{9}\)
AB కి సమాంతరంగా మరియు A(1, -1) గుండా పోతుంది.
AB సమీకరణము y + 1 = – \(\frac{2}{9}\) (x – 1)
9y + 9 = -2x + 2
2x + 9y + 7 = 0

III.

ప్రశ్న 1.
x + 2y = 0, 4x + 3y – 5 = 0, 3x + y = 0 రేఖలతో ఏర్పడిన త్రిభుజానికి లంబకేంద్రం కనుక్కోండి.

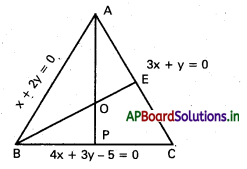
సాధన:
AB సమీకరణం x + 2y = 0 ……………… (1)
BC సమీకరణం 4x + 3y – 5 = 0 ……………… (2)
AC సమీకరణం 3x + y = 0 ………………. (3)
(1), (2) లను సాధిస్తే A నిరూపకాలు (0,0)

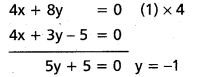
4x – 8 = 0 ⇒ 4x = 8, x = 2
B నిరూపకాలు (2, -1)
BC సమీకరణము 4x + 3y – 5 = 0
AB రేఖ BC కి లంబంగా ఉంది.
ఇది (0, 0) గుండా పోతుంది.
AB సమీకరణము 3x – 4y = 0 ……………… (1)
BE రేఖ AC కి లంబంగా ఉంది.
∴ BE సమీకరణము x – 3y = k
BE రేఖ B (2, -1) గుండా పోతుంది.
2 + 3 = k ⇒ k = 5
BE సమీకరణము x – 3y – 5 = 0 ……………….. (2)

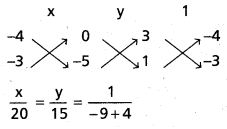
x = -4, y = -3
∴ లంబకేంద్రం 0 (- 4, – 3)

ప్రశ్న 2.
x + y + 2 = 0, 5x-y-2= 0, x – 2y + 5 = 0 భుజాలుగా గల త్రిభుజానికి పరికేంద్రం కనుక్కోండి. [Mar. ’14]
సాధన:
దత్త రేఖలు x + y + 2 = 0 ……………… (1)
5x – y – 2 = 0 ……………. (2)
x – 2y + 5 = 0 …………….. (3)
(1), (2) ల ఖండన బిందువు A = (0, -2)
(2), (3) ల ఖండన బిందువు B = (1, 3)
(1), (3) ల ఖండన బిందువు C = (-3, 1)
S = (α, β) ∆ ABC త్రిభుజానికి పరికేంద్రం.
SA = SB = SC
⇒ SA² = SB² = SC²
⇒ (α – 0)² + (β + 2)² = (α – 1)² + (β – 3)²
= (α + 3)² + (β – 1)²

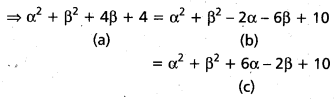
(a) = (b) ⇒ α² + β² + 4β + 4 = α² + β² – 2α – 6β + 10
⇒ 2α + 10β – 6 = 0
⇒ α + 5β – 3 = 0 …………….. (4)
(a) = (c) α² + β² + 4β + 4 = α² + β² + 6α – 2β + 10
⇒ 6α – 6β + 6 = 0
⇒ α – β + 1 = 0 ……………… (5)
(4), (5) ల నుండి

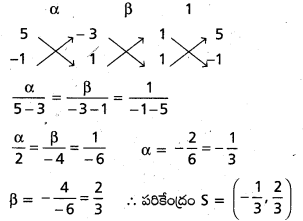
ప్రశ్న 3.
(1, 1) గుండాపోతూ, (-2, 3) నుంచి 3 యూనిట్ల దూరంలో గల సరళరేఖల సమీకరణాలను కనుక్కోండి.
సాధన:
AB రేఖ A(1, 1) గుండా పోతుంది.
AB వాలు ‘m’ అనుకుందాం.
AB సమీకరణము y – 1 = m(x – 1)
mx – m
mx – y + (1 – m) = 0. ……………… (1)
(−2, 3) నుండి AB కి లంబదూరము = 3
\(\frac{|-2 m-3+1-m|}{\sqrt{m^2+1}}\) = 3
వర్గీకరించి అడ్డగుణకారము చేయగా
(3m + 2)² = 9(m² + 1)
9m² + 4 + 12m = 9m² + 9
12m = 5 ⇒ m = \(\frac{5}{12}\)
m² గుణకం = 0 ⇒ m = ∞

i) m = ∞
AB ఊర్ధ్వ రేఖ
AB సమీకరణము x = a
AB రేఖ A(1, 1) గుండా పోతుంది.
∴ a = 1
AB సమీకరణము x = 1

ii) m = \(\frac{5}{12}\)
(1) లో ప్రతిక్షేపించగా
AB సమీకరణము \(\frac{5}{12}\) x – y + [1 – \(\frac{5}{12}\)] = 0
\(\frac{5}{12}\) x – y + \(\frac{7}{12}\) = 0
5x – 12y + 7 = 0

ప్రశ్న 4.
x sec α + y cosec α = a, x cos α y sin α = a cos 2α మూలబిందువు నుంచి లంబదూరాలు p, q అయితే 4p² + q² = a² అని చూపండి. [May ’13]
సాధన:
AB సమీకరణము x sec α + y cosec α = a,
\(\frac{x}{\cos \alpha}+\frac{y}{\sin \alpha}\) = a
x sin α + y cos α = a sin α cos α
x sin α + y cos α – a sin α cos α = 0
p = 0 ల నుండి AB మీదకు లంబదూరము
= \(\frac{|0+0-a \sin \alpha \cos \alpha|}{\sqrt{\sin ^2 \alpha+\cos ^2 \alpha}}\)
= a sin α. cos α = a . \(\frac{\sin 2 \alpha}{2}\)
2p = a sin 2α ………………. (1)
CD సమీకరణము x cos α – y sin α = a cos 2α
x cos α – y sin α – a cos 2α = 0
q = 0 నుండి CD మీదకు లంబదూరము
\(\frac{|0+0-a \cos 2 \alpha|}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\) = a cos 2α ……………… (2)
(1), (2) లను వర్గీకరించగా
4p² + q² = a² sin² 2α + a² cos² 2α
= a² (sin2 2α + cos2 2α)
= a².1
= a²

ప్రశ్న 5.
4x + 5y = 0, 7x + 2y = 0 లు ఒక సమాంతర చతుర్భుజం ఆసన్న భుజాలు 11x + 7y = 9 దాని ఒక వికర్ణం అయితే మిగిలిన రెండు భుజాలు, మరో వికర్ణం సమీకరణాలను కనుక్కోండి.
సాధన:
\(\overleftrightarrow{O A}\), \(\overleftrightarrow{O B}\) లు సమాంతర చతుర్భుజ ఆసన్న భుజాలు
OA, OB ల సమీకరణాలు
4x + 5y = 0 ……………….. (1)
7x + 2y = 0 ………………. (2)
\(\overleftrightarrow{A B}\) 11x + 7y – 9 = 0 ………………… (3)

(1), (2) లను సాధించగా O = (0, 0)
(1), (3) లను సాధించగా

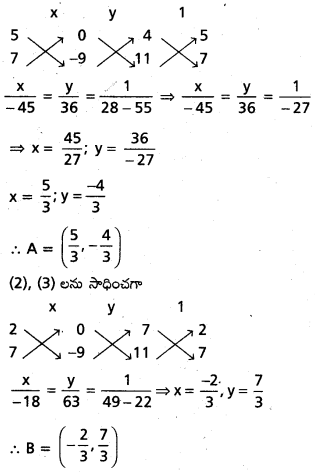
AB మధ్యబిందువు P\(\left(\frac{1}{2}, \frac{1}{2}\right)\). OP వాలు 1.
x = y
BC రేఖ BA కు సమాంతరము
BC సమీకరణము 4x + 5y = k
BC రేఖ B\(\left(-\frac{2}{3}, \frac{7}{3}\right)\) గుండా పోతుంది.
\(4\left(-\frac{2}{5}+51 \frac{7}{3}\right)\) = k
k = \(\frac{35-8}{3}=\frac{27}{3}\) = 9
BC సమీకరణము 4x + 5y = 9
AC రేఖ OB సమాంతరము
AC సమీకరణము 7x + 2y = k
AC రేఖ A\(\left(\frac{5}{3}-\frac{4}{3}\right)\) గుండా పోతుంది.
7\(\left(\frac{5}{3}\right)\) + 2\(\left(-\frac{4}{3}\right)\) = k
k = \(\frac{35-8}{3}=\frac{27}{3}\) = 9
AC సమీకరణము 7x + 2y = 9.

ప్రశ్న 6.
కింద ఇచ్చిన భుజాలు గల త్రిభుజం అంతరకేంద్రాన్ని కనుక్కోండి.
i) x + 1 = 0, 3x – 4y = 5, 5x + 12y = 27
ii) x + y – 7 = 0, x – y + 1 = 0, x – 3y + 5 = 0
సాధన:
i)

∆ ABC
AC సమీకరణము
x + 1 = 0 …………….. (1)
AB సమీకరణము
3x – 4y – 5 = 0 …………….. (2)
BC సమీకరణము
5x + 12y – 27 = 0 ………………. (3)
(1) నుండి x = -1
(2) లో ప్రతిక్షేపించగా ⇒ 3 (-1) – 4y – 5 = 0
4y = – 8
y = -2
(1), (2) ల ఖండన బిందువు
A = (-1,-2)
(2), (3) లను సాధించగా

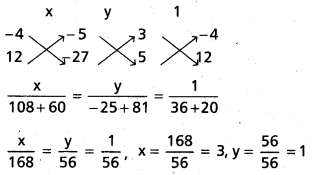
(2), (3) ల ఖండన బిందువు B = (3, 1)
(1) నుండి x = -1
(3) లో ప్రతిక్షేపించగా
-5 + 12y – 27 = 0
12y = 32
y = \(\frac{32}{12}\) = \(\frac{8}{3}\)
(3), (1) ల ఖండన బిందువు

∴ అంతర కేంద్రము = \(\left(\frac{1}{3}, \frac{2}{3}\right)\)

ii)

∆ ABC,
AC సమీకరణము x + y – 7 = 0 ………………. (1)
AB సమీకరణము’ x – y + 1 = 0 ……………….. (2)
BC సమీకరణము x – 3y + 5 = 0 ……………… (3)
(1), (2), (3) లను సాధిస్తే
శీర్షాలు A (3, 4) B (1, 2), C (4, 3)

ప్రశ్న 7.
ax + by + c = 0, lx + my + n = 0, px + qy + r = 0 రేఖలతో ఒక త్రిభుజం ఏర్పడింది. అది సమకోణ త్రిభుజం కాకపోతే,
\(\frac{a x+b y+c}{a p+b q}=\frac{l x+m y+n}{l p+m q}\) -సమీకరణం సూచించే సరళరేఖ ఆ త్రిభుజం లంబకేంద్రం గుండా పోతుందని చూపండి.
సాధన:
దత్త త్రిభుజము

ax + by + c = 0 ………………. (1)
lx + my + n = 0 ………………. (2)
px + qy + r = 0 ………………. (3)
(1), (2) ల ఖండన బిందువు గుండా పోతే రేఖ సమీకరణం.
ax + by + c + k (lx + my + n) = 0
(a + kl) x + (b + km)y + (c + nk) = 0
ఇది (3) కి లంబం కనుక
p(a + kl) + q(b + km) = 0
⇒ k = –\(\frac{\mathrm{ap}+\mathrm{bq}}{l p+\mathrm{m} q}\)
(4) లో ప్రతిక్షేపించగా
(ap + bq + c) – \(\left(\frac{a p+b q}{l p+m q}\right)\) (lx + my + n) = 0
∴ \(\frac{a x+b y+c}{a p+b q}=\frac{l x+m y+n}{l p+m q}\)
కావలసిన రేఖ AD సమీకరణము
ఈ ఉన్నతి A గుండాపోతుంది.
∴ ఈ రేఖ. \(\frac{a x+b y+c}{a p+b q}=\frac{l x+m y+y}{l p+m q}\)
త్రిభుజ లంబకేంద్రం గుండాపోతుంది.

ప్రశ్న 8.
ఒక త్రిభుజం భుజాలు \(\overleftrightarrow{B C}, \overleftrightarrow{C A}, \overleftrightarrow{A B}\) కార్టీసియన్ సమీకరణాలు క్రమంగా u_r = a_rx + b_ry + c_r = 0, r = 1, 2, 3. A గుండాపోతూ \(\overleftrightarrow{B C}\) ని సమద్విఖండన చేసే సరళరేఖ సమీకరణం \(\frac{u_3}{a_3 b_1-a_1 b_3}=\frac{u_2}{a_1 b_2-a_2 b_1}\) అని చూపండి.
సాధన:
u₂ = 0, u₃ = 0 ల ఖండన బిందువు A.
∴ A గుండా పోయే రేఖ సమీకరణము
u₂ + λu₃ = 0⇒ (a₂x + b₂y + c₂) + λ(a₃x + b₃y + C₃) = 0 ………………. (1)
⇒ (a₂ + λa₃)x + (b₂ + λb₃) y + (c₂ + λc₃) = 0
ఈ రేఖ a₁x + b₁y + c₁ = 0 కి సమానం.
\(-\frac{\left(a_2+\lambda a_3\right)}{\left(b_2+\lambda b_3\right)}=-\frac{a_1}{b_1}\)
⇒ (a₂ + λa₃) b₁ = (b₂ + λb₃) a₁
⇒ a₂b₁ +λa₃b₁ = a₁b₂ + λa₁ b₃
⇒ λ (a₃b₁ − a₁b₃) = – (a₂b₁ – a₁b₂)
⇒ λ = – \(\frac{\left(a_2 b_1-a_1 b_2\right)}{a_3 b_1-a_1 b_3}\)
λ విలువను (1) లో ప్రతిక్షేపిస్తే కావలసిన సమీకరణము
(a₂x + b₂y + c₂) – \(\frac{\left(a_2 b_1-a_1 b_2\right)}{\left(a_3 b_1-a_1 b_3\right)}\) (a₃x + b₃y + c₃) = 0
⇒ (a₃b₁ – a₁b₃) (a₂x + b₂y + c₂) – (a₂b₁ – a₁b₂) (a₃x + b₃y + c₃) = 0
⇒ (a₃b₁ − a₁b₃) u₂ – (a₂b₁ – a₁b₂) u₃ = 0
⇒ (a₃b₁ – a₁b₃) u₂ = (a₂b₁ – a₁b₂) u₃
⇒ \(\frac{u_3}{\left(a_3 b_1-a_1 b_3\right)}=\frac{u_2}{\left(a_2 b_1-a_1 b_2\right)}\)