AP Inter 1st Year Maths 1B Solutions Chapter 4 సరళరేఖాయుగ్మాలు Ex 4(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 4 సరళరేఖాయుగ్మాలు Exercise 4(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 4 సరళరేఖాయుగ్మాలు Exercise 4(a)

అభ్యాసం – 4 (a)

I.

ప్రశ్న 1.
ఈ క్రింద ఇచ్చిన ప్రతీ సరళరేఖాయుగ్మపు మధ్య లఘు కోణాన్ని కనుక్కోండి.
i) x² – 7xy + 12y² = 0
ii) y² – xy – 6x² = 0
iii) (x cos α- y sin α)² = (x² + y²) sin² α
iv) x² + 2xy cot α – y² = 0
సాధన:
i) x² – 7xy + 12y² = 0
a = 1, b = 12, h = –\(\frac{7}{2}\)
tan θ = \(\frac{2 \sqrt{h^2-a b}}{a+b}\)
= \(\frac{2 \sqrt{\frac{49}{4}-12}}{1+12}=\frac{2 \sqrt{\frac{1}{4}}}{13}=\frac{\sqrt{1}}{13}\)
tan θ = \(\frac{1}{13}\) ⇒ θ = tan^-1 \(\left(\frac{1}{13}\right)\)

ii) y² – xy – 6x² = 0
a = – 6, b = 1, h = –\(\frac{1}{2}\)

iii) (x cos α- y sin α)² = (x² + y²) sin² α
x² cos² α + y² sin² α – 2xy cos α sin α = x² sin² α + y² sin²α
.. x² (cos² α – sin² α) – 2xy cos α sin α = 0
x² . cos 2α – xy sin 2α = 0
a = cos 2α, b = 0, 2h = – sin 2α
cos θ = \(\frac{|\cos 2 \alpha+0|}{\sqrt{(\cos 2 \alpha-0)^2+\sin ^2 2 \alpha}}\)
= cos 2α
∴ θ = 2α

iv) x² + 2xy cot α – y² = 0
a + b = 1 – 1 = 0
∴ θ = \(\frac{\pi}{2}\)

II.

ప్రశ్న 1.
క్రింద సరళరేఖాయుగ్మాల జతలు ఇవ్వడమైంది. వాటిలో ప్రతీ జతకి ఒకే కోణీయ సమద్విఖండన రేఖాయుగ్మం ఉంటుందని చూపండి. (అంటే ప్రతి జతలోను ఒకే రేఖా యుగ్మంలోని రేఖలు రెండో రేఖాయుగ్మంలోని రేఖలతో సమాన నిమ్నత కలిగి ఉంటాయి.)
i) 2x² + 6xy + y² = 0,
4x² + 18xy + y² = 0.
ii) a²x² + 2h(a + b) xy + b²y² = 0,
ax² + 2hxy + by² = 0; a + b ≠ 0.
iii) ax² + 2hxy + by² + 2(x² + y²) = 0; (λ ∈ R),
ax² + 2hxy + by² = 0.

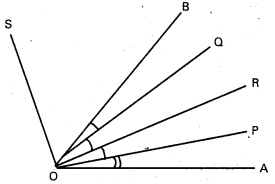
సాధన:
i) OA, OB ల ఉమ్మడి సమీకరణము
2x² + 6xy + y² = 0
కోణ సమద్విఖండన రేఖల సమీకరణము
3(x² – y²) = (2 – 1) xy
3(x² – y²) = xy ……………….. (1)
OP, OQ ల ఉమ్మడి సమీకరణము
4x² + 18xy + y² = 0
కోణ సమద్విఖండన రేఖల సమీకరణం
9(x² – y²) = (4 − 1) xy
9(x² – y²) = 3xy
3(x² – y²) = xy ……………….. (2)
(1), (2) ఒక్కటే కనుక
∴ OA, OB లు OP, OQ లు సమాన నిమ్నత కలిగి ఉన్నాయి.

ii) OA, OB ల ఉమ్మడి సమీకరణము
a²x² + 2h(a + b) xy + b²y² = 0
కోణ సమద్విఖండన రేఖల సమీకరణము
h (a + b) (x² – y²) = (a² – b²) xy
h (a + b) (x² – y²) = (a + b)(a – b) xy
i.e., h(x² – y²) = (a – b) xy ……………. (1)
OP, OQ ల ఉమ్మడి సమీకరణము
ax² + 2hxy + by² = 0
కోణ సమద్విఖండన రేఖల సమీకరణము
h (x² – y²) = (a – b) xy ………………. (2)
(1), (2) ఒకటే
∴ OA, OB లు OP, OQ లు సమాన నిమ్నత కలిగి ఉన్నాయి.

iii) OA, OB ల ఉమ్మడి సమీకరణము
ax² + 2hxy + by² + 2 (x² + y²) = 0
(a + λ) x² + 2hxy + (b + 2λ) y² = 0
OA, OB ల కోణ సమద్విఖండన రేఖల సమీకరణము
h (x² – y²) = (a + λ – b – λ)xy
= (a – b) xy ……………… (1)
OP, OQ ల ఉమ్మడి సమీకరణము
ax² + 2hxy + by² = 0
OP, OQ ల సమద్విఖండన రేఖల సమీకరణము
h(x² – y²) = (a – b) xy ……………… (2)
(1), (2) ఒకటే కనుక
∴ OA, OB లు OP, OQ లు సమాన నిమ్నత కలిగి ఉన్నాయి.

ప్రశ్న 2.
6x² + 2hxy + y² = 0 తో సూచించే సరళరేఖల వాలులు 1 : 2 నిష్పత్తిలో ఉంటే h విలువ కనుక్కోండి.
సాధన:
దత్త రేఖల ఉమ్మడి సమీకరణము
6x² + 2hxy + y² = 0
వాటి విడివిడి సమీకరణాలు
y = m₁x మరియు y = m₂x అనుకొనుము.
∴ m₁ + m₂ = \(\frac{-2 h}{6}=-\frac{h}{3}\) , m₁m₂ = \(\frac{1}{6}\)
దత్తాంశం \(\) ⇒ m₂ = 2m₁
3m₁ = –\(\frac{h}{3}\) ; 2m₁² = \(\frac{1}{6}\)
m₁ = –\(\frac{h}{9}\) ; m₁² = \(\frac{1}{12}\)
\(\left(-\frac{\mathrm{h}}{9}\right)^2=\frac{1}{12}\)
\(\frac{h^2}{81}=\frac{1}{12}\)
h² = \(\frac{81}{12}=\frac{27}{4}\)
h = ± \(\sqrt{\frac{27}{4}}=\pm \frac{3 \sqrt{3}}{2}\)

ప్రశ్న 3.
ax² + 2hxy + by² = 0 ఒక రేఖాయుగ్మింలోని రేఖలలో ఒక దాని వాలు రెండో దాని వాలుకు రెట్టింపయితే 8h² = 9ab అని చూపండి
సాధన:
దత్త రేఖలు ఉమ్మడి సమీకరణము
ax² + 2hxy + by² = 0
y = m₁x మరియు y = m₂x లు వాటి విడి విడి సమీకరణాలు అనుకొందాం.
∴ m₁ + m₂ = –\(\frac{2 h}{b}\), m₁m₂ = \(\frac{a}{b}\)
m₂ = 2m₁ కనుక
∴ 3m₁ = –\(\frac{2 h}{b}\) ; 2m₁² = \(\frac{a}{b}\)
m₁ = – \(\frac{2 h}{3}\) ; m₁² = \(\frac{a}{2b}\)
∴ \(\left(-\frac{2 h}{3 b}\right)^2=\frac{a}{2 b}\)
\(\frac{4 h^2}{9 b^2}=\frac{a}{2 b}\)
8h² = 9ab.

ప్రశ్న 4.
మూలబిందువు గుండా పోతూ 3x – y – 1 = 0 అనే సరళరేఖతో 30° కోణం చేసే సరళరేఖాయుగ్మం సమీకరణం 13x² + 12xy – 3y = 0 అని చూపండి.

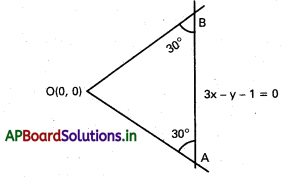
సాధన:
AB సమీకరణము 3x – y – 1 = 0
OA, OB లు AB తో 30° కోణం చేస్తూ మూలబిందువు గుండా పోతుంది.
OA వాలు m అనుకొందాం.
∴ OA సమీకరణము
y – 0 = m (x − 0) = mx లేదా mx – y = 0
cos ∠OAB = \(\frac{|3 m+1|}{\sqrt{9+1} \sqrt{m^2+1}}\)
cos ∠OAB = cos 30° = \(\frac{\sqrt{3}}{2}\)
∴ \(\frac{\sqrt{3}}{2}=\frac{|3 m+1|}{\sqrt{10} \sqrt{m^2+1}}\)
వర్గీకరించి, అడ్డ గుణకారము చేయగా,
\(\frac{3\left(m^2+1\right)}{4}=\frac{(3 m+1)^2}{10}\)
15(m² + 1) = 2 (3m + 1)²
15m² + 15 = 2 (9m² + 6m + 1)
= 18m² + 12m + 2
3m² + 12m – 13 = 0
m₁, m₂ లు మూలాలనుకుందాం.
m₁ + m₂ = -4, m₁ m₂ = \(\frac{-13}{3}\)
OA, OB ల ఉమ్మడి సమీకరణము
(m₁x – y) (m₁x – y) = 0
m₁m₁ x² – (m₁ + m₂) xy + y² = 0
\(\frac{-13}{3}\) x² + 4xy + y² = 0
-13x² + 12 xy + 3y² = 0 (లేదా)
13x² – 12xy – 3y² = 0

ప్రశ్న 5.
మూలబిందువు గుండాపోతూ x + y + 5 = 0 సరళరేఖతో లఘుకోణం α చేసే సరళరేఖాయుగ్మం సమీకరణం కనుక్కోండి.

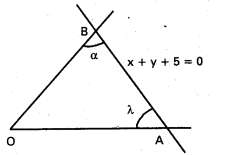
సాధన:
AB సమీకరణము x + y + 5 = 0
AB వాలు = -1
OA, OB లు కావలసిన రేఖలు
OA సమీకరణము y = mx ⇒ mx – y = 0
cos α = \(\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\)
= \(\frac{|m-1|}{\sqrt{2} \sqrt{m^2+1}}\)
2(m² + 1) cos² α = (m – 1)²
2(m² + 1) = \(\frac{(m-1)^2}{\cos ^2 \alpha}\) = (m – 1)² sec² α.
2m² + 2 = m² sec² α – 2m sec² α + sec² α.
m² (sec² α – 2) – 2m sec² α + (sec² α – 2) = 0
m₁ + m₁ = \(\frac{2 \sec ^2 \alpha}{\sec ^2 \alpha-2}\), m₁m₂ = 1
OA, OB ల ఉమ్మడి సమీకరణము
(y – m₁x) (y – m₂x) = 0
y² – (m₁ + m₂) xy + m₁m₂ x² = 0
y² + \(\frac{2 \sec ^2 \alpha}{\sec ^2 \alpha-2}\) . xy + x² = 0
m₁ + m₂ = \(\frac{2 \sec ^2 \alpha}{\sec ^2 \alpha-2}=\frac{2}{1-2 \cos ^2 \alpha}\)
= \(\frac{-2}{2 \cos ^2 \alpha-1}=\frac{-2}{\cos 2 \alpha}\)
= 2 sec 2 α
OA, OB ల ఉమ్మడి సమీకరణాలు
x² + 2xy sec 2α + y² = 0

ప్రశ్న 6.
(x + 2a)² – 3y² = 0, x = లు సూచించే రేఖలు ఒక సమబాహు త్రిభుజాన్ని ఏర్పరుస్తాయని చూపండి.
సాధన:
OA, OB ల ఉమ్మడి సమీకరణము
(x + 2a)² – 3y² = 0
(x + 2a)² – (\(\sqrt{3}\)y)² = 0
(x + 2a + \(\sqrt{3}\) y) (x + 2a – \(\sqrt{3}\)y) = 0

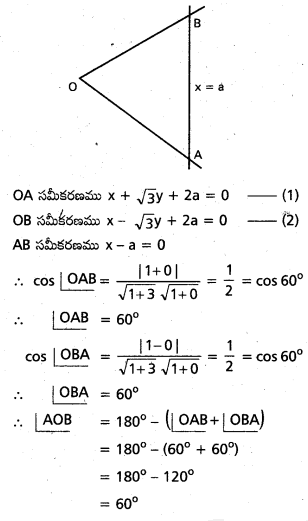
∴ ∆OAB సమబాహు త్రిభుజం.

ప్రశ్న 7.
(ax + by)² = c(bx – ay)², c > 0 తో సూచించే సరళరేఖల మధ్యకోణాల సమద్విఖండన రేఖలు ax+ by + k= 0 సరళరేఖకు సమాంతరంగాను, లంబంగాను ఉంటాయని చూపండి.
సాధన:
దత్త రేఖల ఉమ్మడి సమీకరణాలు,
(ax + by)² = c (bx – ay)²
a²x² + b²y² + 2ab xy = c (b²x² + a²y² – 2abxy)
= c b²x² +ca²y² – 2cabxy
(a² – cb²)x² + 2ab (1 + c²) xy + (b² – ca²)y² = 0
కోణ సమద్విఖండన రేఖల సమీకరణము
h (x – y²) = (a – h) xy
ab (1 + c) (x² – y²)
= (a² – cb² – b² + ca²) (x² – y²) = 0
= (a² – b²)(1 + c) xy.
i.e., ab (x² – y²) – (a² – b²) xy = 0
(ax + by) (bx – ay) = abx² – a²xy + b²xy – aby²
= ab (x² – y²) – (a² – b²) xy
∴ కోణ సమద్విఖండన రేఖల సమీకరణము
(ax + by) (bx – ay) = 0
సమద్విఖండన రేఖలు ax + by = 0 మరియు bx – ay = 0
ax + by = 0 కు సుమాంతరం ax + by + k = 0
bx – ay = 0 కు సుమాంతరం ax + by + k = 0.

ప్రశ్న 8.
2x² – 5xy + 3y² = 0 అనే సమీకరణం ఒక సమాంతర చతుర్భుజపు రెండు పక్క భుజాలను సూచిస్తుంది. దీని వికర్ణాలలో ఒకదాని సమీకరణం x + y + 2 = 0 అయితే, ఆ సమాంతర చతుర్భుజపు శీర్షాలు, రెండో వికర్ణం సమీకరణం కనుక్కోండి.

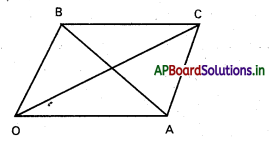
సాధన:
OA, OB ల ఉమ్మడి సమీకరణము
2x² – 5xy + 3y² = 0 …………… (1)
AB సమీకరణము x + y + 2 = 0
y = (x + 2)
(1) లో ప్రతిక్షేపించగా
2x² + 5x (x + 2) + 3(x + 2)² = 0
2x² + 5x² + 10x + 3(x² + 4x + 4) = 0
7x² + 10x + 3x² + 12x + 12 = 0
10x² + 22x + 12 = 0
5x² + 11x + 6 = 0
(x + 1) (5x + 6) = 0
x + 1 = 0 లేదా 5x + 6 = 0
x = – 1 లేదా 5x = – 6
x = –\(\frac{6}{4}\)
y = (x + 2)
x = -1 ⇒ y = -(-1 + 2) = -1
⇒ A నిరూపకాలు (−1, -1)
x = –\(\frac{6}{5}\) ⇒ y = -(-\(\frac{6}{5}\) + 2) = –\(\frac{4}{5}\)
⇒ B నిరూపకాలు \(\left(-\frac{6}{5},-\frac{4}{5}\right)\)
కర్ణాలు AB, OC లు ‘O’ వద్ద ఖండించుకొంటాయి.
AB, OC ల మధ్యబిందువు
C నిరూపకాలు (x, y) అనుకుందాము.
OC మధ్యబిందువు = AB మధ్య బిందువు
\(\left(\frac{x}{2}, \frac{y}{2}\right)=\left(\frac{-1-\frac{6}{5}}{2}, \frac{-1-\frac{4}{5}}{2}\right)\)
∴ x = -1 – \(\frac{6}{5}\) = –\(\frac{11}{5}\) ;
y = -1 – \(\frac{4}{5}\) = –\(\frac{9}{5}\)
C నిరూపకాలు \(\left(-\frac{11}{5},-\frac{9}{5}\right)\)
∴ శీర్షాలు O(0, 0), A (-1, -1)
C\(\left(-\frac{11}{5},-\frac{9}{5}\right)\) , B\(\left(-\frac{6}{5},-\frac{4}{5}\right)\)
OC సమీకరణము y – 0 = \(\frac{\frac{-9}{5}}{\frac{-11}{5}}(x-0)\)
y = \(\frac{9}{11}\) ⇒ 11y = 9x
లేదా 9x – 11y = 0

ప్రశ్న 9.
కింది రేఖలతో ఏర్పడే త్రిభుజం కేంద్రభాసం, వైశాల్యం కనుక్కోండి.
i) 2y² – xy – 6x² = 0, x + y + 4 = 0
ii) 3x² – 4xy + y² = 0, 2x – y = 6

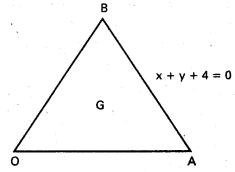
సాధన:
i) OA, OB ల ఉమ్మడి సమీకరణాలు
2y² – xy – 6x² = 0 …………….. (1)
AB సమీకరణము x + y + 4 = 0
y = -(x + 4) ……………… (2)
(1) లో ప్రతిక్షేపించగా
2(x + 4)² + x (x + 4) – 6x² = 0
2(x² + 8x + 16) + x² + 4x – 6x² = 0
2x² + 16x + 32 + x² + 4x – 6x² = 0
-3x² + 20x + 32 = 0
3x² – 20x – 32 = 0
(3x + 4) (x – 8) = 0
3x + 4 = 0 లేదా x – 8 = 0
3x = -4 లేదా x = 8
x = –\(\frac{4}{3}\) లేదా 8

సందర్భం (i) : x = –\(\frac{4}{3}\)
y = – (x + 4)
= -(\(\frac{-4}{3}\) + 4) = –\(\frac{8}{3}\)
A నిరూపకాలు \(\left(-\frac{4}{3},-\frac{8}{3}\right)\)

సందర్భం (ii) : x = 8
y = – (x + 4) = – (8 + 4) = -12
B నిరూపకాలు (8, – 12)
∆AOB కేంద్ర భాసము G అనుకుందాం.
G నిరూపకాలు

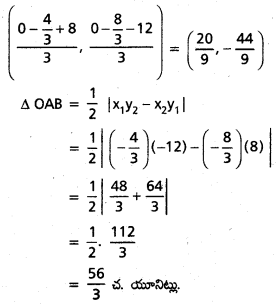
ii) OA, OB ల ఉమ్మడి సమీకరణము,
3x² – 4xy + y² = 0 ……………. (1)
AB సమీకరణము 2x – y = 6
y = 2x – 6 ……………… (2)
(1) లో ప్రతిక్షేపించగా
3x² – 4x (2x – 6) + (2x – 6)² = 0
3x² – 8x² + 24x + 4x² + 36 – 24x = 0
-x² + 36 = 0
x² – 36 = 0
(x + 6) (x – 6) = 0
x + 6 = 0 లేదా x – 6 = 0
x = 6 లేదా 6
y = 2x – 6
x = 6y ⇒ y = 12 – 6 = 6
A నిరూపకాలు (6, 6)
x = -6y ⇒ u = -12 – 6 = -18
B నిరూపకాలు (-6, 18)
G నిరూపకాలు
\(\left(\frac{0+6-6}{3}, \frac{0+6-18}{3}\right)\) = (0, -4)
∆ OAB = \(\frac{1}{2}\)|x₁y₂ – x₂y₁|
= \(\frac{1}{2}\)|(6 (-18) – (-6) . 6|
= \(\frac{1}{2}\) |-108 + 36
= \(\frac{1}{2}\) . 72 = 36 చ. యూనిట్లు

ప్రశ్న 10.
(2, -1) బిందువు వద్ద ఖండించుకొంటూ 6x² – 13xy – 5y² = 0 సూచించే రేఖాయుగ్మానికి
i) లంబంగా ఉండే రేఖాయుగ్మపు సమీకరణం,
ii) సమాంతరంగా ఉండే రేఖాయుగ్మపు సమీకరణం కనుక్కోండి.
సాధన:
OA, OB ల సమీకరణము 6x² – 13xy – 5y² = 0
i) (x₁, y₁) గుండా పోతూ
ax² + 2hxy + by² = 0 కు లంబంగా ఉండే రేఖా సమీకరణము
b (x – x₁)² – 2h (x – x₁) (y – y₁) + a (y – y₁)² = 0
లంబరేఖల సమీకరణము
-5(x – 2)² + 13(x – 2) (y + 1) + 6(y + 1)² = 0
-5(x² – 4x + 4) + 13 (xy + x – 2y – 2) + 6 (y² + 2y + 1) = 0
-5x² + 20x – 20 + 13xy + 13x – 26y – 26 + 6y² + 12y + 6 = 0
-5x² + 13xy + 6y²+ 33x – 14y – 40 = 0
లేదా 5x² – 13xy – 6y² – 33x + 14y + 40 = 0

ii) (x₁, y₁) గుండాపోతూ ax² + 2hxy + by² = 0
సమాంతరంగా ఉండే రేఖల సమీకరణము
a (x – x₁)² + 2h (x – x₁) (y – y₁) + b(y – y₁)² = 0
సమాంతర రేఖల సమీకరణము
6 (x − 2)² – 13 (x − 2) (y + 1) − 5 (y + 1)² = 0
6 (x² – 4x + 4) – 13 (xy + x – 2y – 2) – 5 (y² + 2y + 1) = 0
6x² – 24x + 24 – 13xy – 13x + 26y + 26 – 5y² – 10y – 5 = 0
6x² – 13xy – 5y² – 37x + 16y + 45 = 0.

ప్రశ్న 11.
3x – 4y + 7 = 0, 12x + 5y – 2 = 0 సరళరేఖల మధ్య లఘుకోణ సమద్విఖండన రేఖ సమీకరణం కనుక్కోండి.
సాధన:
దత్త రేఖలు 3x – 4y + 7 = 0 ……………… (1)
12x + 5y – 2 = 0 ……………….. (2)
(1) & (2) రేఖల కోణ సమద్విఖండన రేఖల సమీకరణము
\(\frac{3 x-4 y+7}{\sqrt{3^2+4^2}} \pm \frac{12 x+5 y-2}{\sqrt{12^2+5^2}}\) = 0
⇒ \(\frac{3 x-4 y+7}{5} \pm \frac{12 x+5 y-2}{13}\) = 0
13 (3x – 4y + 7) ± 5 (12x + 5y – 2) = 0
(39x – 52y + 91) ± (60x + 25y -10) = 0
(i) 39x – 52y + 91 + 60x + 25y – 10 = 0
99x – 27y + 81 = 0 ……………… (3)
లేదా 11x – 3y + 9 = 0

(ii) (39x – 52y + 51) – (60x + 25y – 10) = 0
39x – 52y + 51 – 60x – 25y + 10 = 0
– 21x – 77y + 61 = 0
21x + 77y – 61 = 0 …………….. (4)
(1), (4) రేఖల మధ్య కోణము ‘0’ అయితే
tan θ = + \(\left|\frac{a_1 b_2-a_2 b_1}{a_1 a_2+b_1 b_2}\right|=\left|\frac{231+84}{63-308}\right|\)
= \(\frac{315}{225}\) > 1
∴ (4) గురు కోణ సమద్విఖండన రేఖ (3) సూచించే రెండవది లఘుకోణ సమద్విఖండన రేఖ.
∴ 11x – 3y + 9 = 0 రేఖ లఘుకోణ సమద్విఖండన రేఖ.

ప్రశ్న 12.
x + y – 5 = 0, x – 7y + 7 = 0 అనే సరళరేఖల మధ్య అధిక (గురు) కోణ సమద్విఖండన రేఖ సమీకరణం కనుక్కోండి.
సాధన:
దత్త రేఖలు
x + y – 5 = 0 …………….. (1)
x – 7y + 7 = 0 ………………… (2)
(1), (2) మధ్యకోణ సమద్విఖండన రేఖలు
\(\frac{x+y-5}{\sqrt{1+1}} \pm \frac{x-7 y+7}{\sqrt{1+49}}\) = 0
⇒ \(\frac{x+y-5}{\sqrt{2}} \pm \frac{x-7 y+7}{5 \sqrt{2}}\) = 0
⇒ (5x + 5y – 25) ± (x – 7y + 7) = 0
i) 5x + 5y – 25 + x – 7y + 7 = 0
6x – 2y – 18 = 0
3x – y – 9 = 0 ………………. (3)

ii) (5x + 5y – 25) – (x – 7y + 7) = 0
4x + 12y – 32 = 0
x + 3y – 8 = 0 ………………. (4)
(1), (4) రేఖల మధ్య కోణము ‘θ’ అయితే
tan θ = \(\frac{a_1 b_2-a_2 b_1}{a_1 a_2+b_1 b_2}=\frac{3-1}{1+3}=\frac{2}{4}=\frac{1}{2}\) < 1
∴ (4) లఘుకోణ సమద్విఖండన రేఖ గురుకోణ సమద్విఖండన రేఖ సమీకరణము 3x – y – 9 = 0.

III.

ప్రశ్న 1.
(lx + my)² – 3(mx – ly)² = 0, lx + my + n = 0 అనే సరళరేఖలతో ఏర్పడే త్రిభుజం \(\frac{n^2}{\sqrt{3}\left(l^2+m^2\right)}\) వైశాల్యం గల సమబాహు త్రిభుజం అని నిరూపించండి. [T.S Mar. ’15]
సాధన:
OA, OB ల ఉమ్మడి సమీకరణము
(lx + my)² – 3(mx – ly)² = 0
l²x² + m²y² + 21mxy – 3m²x² – 3l² y² + 6 lmxy = 0
(l² – 3m²) x² + 8lmxy + lm² − 3l²) y² = 0
cos ∠AOB = \(\frac{|a+b|}{\sqrt{(a-b)^2+4 n^2}}\)
= \(\frac{\left|l^2-\mathrm{m}^2+\mathrm{m}^2-3 l^2\right|}{\sqrt{\left(l^2-3 \mathrm{~m}^2-\mathrm{m}^2+3 l\right)^2+a l^2 \mathrm{~m}^2}}\)
= \(\frac{2\left|l^2+m^2\right|}{4 \sqrt{\left(l^2-m^2\right)^2+4 l^2 m^2}}=\frac{2\left|l^2+m^2\right|}{4\left(l^2+m^2\right)}=\frac{1}{2}\)
= cos 60°
∠AOB = 60°
OA, OB ల సమద్విఖండన రేఖ ఉమ్మడి సమీకరణము
h (x² – y²) = (a – b) xy
4 lm (x² – y²) = (x² – 3m² – m² + 3l² xy)
4 lm (x² − y²) = 4(l² – m²)
lmx² – (l² – m²)xy – lmy² = 0
(lx – my) (mx – ly) = 0
lx + my = 0 మరియు mx – ly = 0
∴ సమద్విఖండన రేఖ mx – ly = 0 కు లంబంగా ఉంటే
lx + my + n = 0.
OAB సమద్విబాహు త్రిభుజం ∠AOB = 60°
OAB సమబాహు త్రిభుజం
P = P నుండి AB మీదకు లంబదూరం
= \(\frac{|n|}{\sqrt{l^2+m^2}}\)
ΔΟΑΒ = \(\frac{\mathrm{p}^2}{\sqrt{3}}=\frac{\mathrm{n}^2}{\sqrt{3}\left(l^2+\mathrm{m}^2\right)}\) చ. యూనిట్లు.

ప్రశ్న 2.
3x² + 48xy + 23y² = 0, 3x – 2y + 13 = 0 అనే సరళరేఖలతో ఏర్పడే త్రిభుజం \(\frac{13}{\sqrt{3}}\) చ.యూ. వైశాల్యంగా గల సమబాహు త్రిభుజం అని నిరూపించండి.
సాధన:
OA, OB ల ఉమ్మడి సమీకరణాలు
3x² + 48xy + 23y² = 0 …………………. (1)
AB సమీకరణం 3x – 2y + 13 = 0 …………….. (2)
(1) ని
(9x² – 12xy + 4y²) – 3(4x² + 12xy + 9y²) = 0
ఈ విధంగా రాయగలము.
i.e., (3x – 2y)² – 3(2x + 3y)² = 0
⇒ [(3x – 2y) + \(\sqrt{3}\) (2x + 3y)] [(3x – 2y) – \(\sqrt{3}\) (2x + 3y)] = 0
⇒ [(3 + 2\(\sqrt{3}\))x + (3\(\sqrt{3}\) – 2)y] [(3 – 2\(\sqrt{3}\))x – (3\(\sqrt{3}\) + 2)y] = 0
OA సమీకరణము
(3 + 2 \(\sqrt{3}\))x − (3\(\sqrt{3}\) – 2)y = 0 ……………….. (1)
OB సమీకరణము
(3 – 2\(\sqrt{3}\))x – (3\(\sqrt{3}\) + 2)y = 0 ……………….. (2)

∴ OAB సమబాహు త్రిభుజము

ప్రశ్న 3.
ax² + 2hxy + by² = 0 సూచించే రేఖాయుగ్మపు మధ్యకోణాల సమద్విఖండన రేఖాయుగ్మం మధ్య కోణాలను సమద్విఖండన చేసే రేఖాయుగ్మం సమీకరణం (a – b) (x² – y²) + 4hxy = 0 అని నిరూపించండి.
సాధన:
దత్త రేఖల సమీకరణము
ax² + 2hxy + by² = 0
కోణ సమద్విఖండన రేఖల సమీకరణము
h (x² – y²) = (a – b) xy ………………. (1)
hx² – hy² – (a – b) xy = 0
∴ A = h, B = – h; 2H = – (a – b)
(1) యొక్క సమద్విఖండన రేఖల సమీకరణము
H(x² – y²) = (A – B) xy
– \(\frac{(a-b)}{2}\) (x² – y²) = 2hxy
– (a – b) (x² – y²) = 4hxy
లేదా (a – b) (x² – y²) + 4hxy = 0
∴ ax² + 2hyx + by² = 0 ల సమద్విఖండన రేఖల ‘సమీకరణము
(a – b) (x² – y²) + 4hxy = 0.

ప్రశ్న 4.
ax² + 2hxy + by² = 0 సూచించే సరళరేఖలలో ఒక సరళరేఖ నిరూపకాక్షాల మధ్య కోణాన్ని సమద్విఖండన చేస్తే (a + b)² = 4h² అని నిరూపించండి. [June ’04]
సాధన:
నిరూపకాక్షాల కోణ సమద్విఖండన రేఖల సమీకరణాలు
y = ±x.
సందర్భం (i) :
y = x రేఖ ax² + 2hxy + by² = 0 యొక్క ఒక కోణం సమద్విఖండన రేఖ
x² (a + 2h + b) = 0
a + 2h + b = 0 ………………. (1)

సందర్భం (ii) : y = -x రేఖ
ax² + 2hxy + by² = 0 యొక్క ఒక కోణం సమద్విఖండన రేఖ
x² (a – 2h + b) = 0
a – 2h + b = 0 ………………. (2)
(1), (2) లను గుణించగా
(a + b + 2h). (a + b – 2h) = 0
(a + b)² – 4h²
(a + b)² = 4h²

ప్రశ్న 5.
ax² + 2hxy + by² = 0, lx + my = 1 అనే సరళరేఖలలో ఏర్పడే త్రిభుజం కేంద్రాభాసం (α, β) అయితే \(\frac{\alpha}{\mathrm{b} \boldsymbol{l}-\mathrm{hm}}=\frac{\beta}{\mathrm{am}-\mathrm{hl}}=\frac{2}{3\left(\mathrm{~b} \boldsymbol{l}^2-2 \mathrm{~h} \boldsymbol{l} \mathrm{m}+\mathrm{am}{ }^2\right)}\) అని నిరూపించండి.

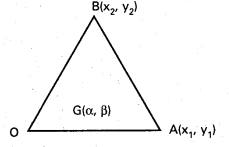
సాధన:
OA, OB ల ఉమ్మడి సమీకరణము
ax² + 2hxy + by² = 0 …………….. (1)
AB సమీకరణము lx + my = 1
my = 1 – lx
y = \(\frac{1-l x}{m}\) …………… (2)
(1) లో ప్రతిక్షేపించగా
ax² + 2hx\(\frac{(1-l x)}{m}\) + b\(\frac{(1-l x)^2}{m^2}\) = 0
am²x² + 2hmx (1 – lx) + b (1 + l²x² – 2lx) = 0
am²x² + 2hmx – 2hlmx² + b + b²x² – 2blx = 0
(am² – 2hlm + bl²) x² – 2(bl – hm) x + b = 0
అనుకుందాం.
A నిరూపకాలు (x₁, y₁), మరియు B నిరూపకాలు (x₂, y₂)
x₁ + x₂ = \(\frac{2(\mathrm{~b} l-\mathrm{hm})}{\mathrm{a} \mathrm{m}^2-2 \mathrm{~h} l \mathrm{~m}+\mathrm{b} l^2}\) ……………. (3)
A, B లు lx + my = 1 మధ్యబిందువులు.
lx₁ + my₁ = 1
lx₂ + my₂ = 1
l (x₁ + x₂) + m(y₁ + y₂) = 2
m(y₁ + y₂) = 2 – l(x₁ + x₂)

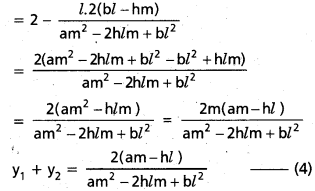
త్రిభుజ శీర్షాల నిరూపకాలు
O (0, 0), A (x₁, y₁), B(x₂, y₂)
G నిరూపకాలు అనుకుందాం.

ప్రశ్న 6.
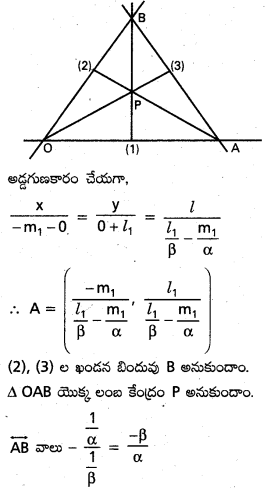
\(\frac{x}{\alpha}+\frac{y}{\beta}\) = 1, ax² + 2hxy + by² = 0 సరళరేఖలతో ఏర్పడే త్రిభుజం లంబకేంద్రానికి, మూలబిందువుకు గల మధ్య దూరం (α² + β²)^1/2 \(\left|\frac{(a+b) \alpha \beta}{a \alpha^2-2 h \alpha \beta+b \beta^2}\right|\) అని నిరూపించండి.
సాధన:
ax² + 2hxy + by² = 0 సూచించే రేఖలు
l₁x + m₁y = 0 ………………. (1)
l₂x + m₂y = 0 ………………… (2)
అనుకొందాం.
∴ (l₁x + m₁y) (l₂x + m₂y) = ax² + 2hxy +by²
ఇరువైపులా పోల్చగా
l₁l₂ = a, m₁m₂ = b, l₁m₂ + l₂ m₁ = 2h
దత్త రేఖ lx + my = 1 ………………….. (3)
(1) & (2) ల ఖండన బిందువులు
(1) & (3) ల ఖండన బిందువు A అనుకొందాం.



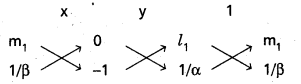
⇒y (l₁α – m₂β) – αβl₁l₂ = m₂(xl₁α – m₁β) + m₁αβ)
⇒ (l₁α – m₁β) (m₂x – l₂y) = m₁m₂αβ + l₁l₂αβ

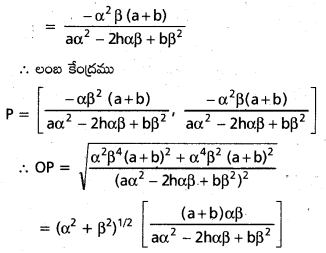
ప్రశ్న 7.
ఒక రేఖాయుగ్మంలో px + qy + r = 0 అనేది ఒక సరళరేఖ. ఆ రేఖాయుగ్మపు మధ్యకోణాల సమద్విఖండన రేఖలో ఒకటి lx + my + n = 0 అయితే, ఆ రేఖాయుగ్మంలో రెండో సరళరేఖ సమీకరణం (px + qy + r) (l² + m²) – 2(lp + mq) (lx + my + n) = 0 అని నిరూపించండి.
సాధన:
lx + my + n = 0.కోణ సమద్విఖండన రేఖ (α, β) మీద బిందువు
lα + mβ + n = 0 ……………… (1)
రెండవ రేఖ, దత్త రేఖల ఖండన బిందువు, కోణ సమద్విఖండన రేఖల ఖండన బిందువు గుండా పోతూ p + λq = 0
దాని సమీకరణము
(px + qy + r) + 2(lx + my + n) = 0
px + py + r = 0
(α, β) కోణ సమద్విఖండన రేఖ మీది బిందువులు. దాని నుండి (2), (3) రేఖల లంబ దూరాలు సమానం.
\(\frac{(p \alpha+q \beta+r)+\lambda(l \alpha+m \beta+n)}{\sqrt{\left[(p+l \lambda)^2+(q+m \lambda)^2\right]}}=\pm \frac{p \alpha+q \beta+r}{\sqrt{p^2+q^2}}\)
(1) లో lα + mβ + n = 0 pα+ qβ + r కొట్టివేసి ఇరువైపుల వర్గీకరించగా
(p + lλ)² + (q + mλ)² = p² + q² లేదా
2λ (pl + qm) + λ² (l² + m²) = 0
.. λ = – 2 \(\frac{\mathrm{p} l+\mathrm{qm}}{l^2+\mathrm{m}^2}\)
λ. విలువ (2) లో ప్రతిక్షేపించగా,
(px + qy + r) + \(\left(\frac{-2 p l+q m}{l^2+m^2}\right)\) lx + my + n = 0
⇒ (px + qy + r) (l² + m²) – 2(pl + qm) (lx + my + n ) = 0