Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 4 సరళరేఖాయుగ్మాలు Exercise 4(c) will help students to clear their doubts quickly.
AP Inter 1st Year Maths 1B Solutions Chapter 4 సరళరేఖాయుగ్మాలు Exercise 4(c)
అభ్యాసం 4 (సి)
I.
ప్రశ్న 1.
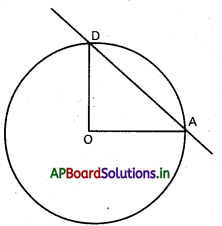
x2 + y2 = 1, x + y = 1 ల ఖండన బిందువులను మూలబిందువుకు కలిపితే వచ్చే సరళరేఖల సమీకరణన్ని కనుక్కోండి.
సాధన:
దత్త వక్రాలు x2 + y 2 = 1 ………………. (1)
x + y = 1 ………………. (2)
(2) సహాయంతో (1) ని సమఘాత పరిస్తే
OA, OB ల ఉమ్మడి సమీకరణం
x2 + y2 = (x + y)2
= x2 + y2 + 2xy
i.e., 2xy = 0 ⇒ xy = 0
ప్రశ్న 2.
y2 = x, x + y = 1 ల ఖండన బిందువులను మూలబిందువుకు కలిపితే వచ్చే సరళరేఖల మధ్య కోణాన్ని కనుక్కోండి.
సాధన:
వక్రం సమీకరణం y2 = x ……………. (1)
AB సమీకరణం x + y = 1 ……………… (2)
(2) సహాయంతో (1) ని సమఘాతపరిస్తే
OA, OB ల ఉమ్మడి సమీకరణం
y2 = x(x + y) = x2+ xy
x2 + xy – y2 = 0
a + b = 1 – 1 = 0
OA, OB లు లంబంగా ఉన్నాయి.
∴ ∠AOB
![]()
II.
ప్రశ్న 1.
x – y – \(\sqrt{2}\) = 0 అనే సరళరేఖల x2 – xy + y2 + 3x + 3y + 2 = 0 అనే వక్రాన్ని ఖండించే బిందువులను మూలబిందువుకు కలిపితే వచ్చే సరళరేఖలు పరస్పరం లంబంగా ఉంటాయని చూపండి. [A.P Mar. ’15, ’12; May. ’12]
సాధన:
వక్రం సమీకరణం
x2 – xy + y2 + 3x + 3y – 2 = 0 ………………. (1)
AB సమీకరణము x – y – \(\sqrt{2}\) = 0
x – y = \(\sqrt{2}\)
\(\frac{x-y}{\sqrt{2}}\) = 1 ……………… (2)
(2) సహాయంతో (1) ని సమఘాతపరిస్తే OA, OB ల ఉమ్మడి సమీకరణం
x2 – xy + y2 + 3x.1 + 3y.1 – 2.12 = 0
x2 – xy + y2 + 3(x + y) \(\frac{x-y}{\sqrt{2}}\) – 2 \(\frac{(x-y)^2}{2}\) = 0
x2 – xy + y2 + \(\frac{3}{\sqrt{2}}\) (x2 – y2) – (x2 – 2xy + y2) = 0
x2 – xy + y2 + \(\frac{3}{\sqrt{2}}\) x2 – \(\frac{3}{\sqrt{2}}\) y2 – x2 + 2xy – y2 = 0
\(\frac{3}{\sqrt{2}}\)x2 + xy – \(\frac{3}{\sqrt{2}}\)y2 = 0
a + b = \(\frac{3}{\sqrt{2}}\) – \(\frac{3}{\sqrt{2}}\) = 0
∴ OA, OB లు లంబంగా ఉన్నాయి.
![]()
ప్రశ్న 2.
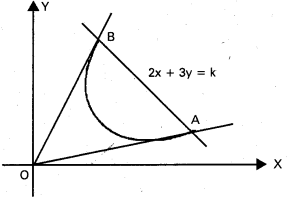
x + 2y = k అనే రేఖ 2x2 – 2xy + 3y2 + 2x – y – 1 = 0 అనేక వక్రాన్ని ఖండించే బిందువులను మూలబిందువుకు కలిపితే వచ్చే రేఖలు పరస్పరం లంబంగా ఉంటే, k విలువలు కనుక్కోండి. [T.S Mar. ’15]
సాధన:
దత్త వక్రం సమీకరణం
S ≡ 2x2 + 2xy + 3y2 + 2x – y – 1 = 0 ……………….. (1)
AB సమీకరణము x + 2y = k
(2) సహాయంతో (1) ని సమఘాత పరిస్తే OA, OB ల ఉమ్మడి సమీకరణం
2x2 – 2xy + 3y2 + 2x.1 – y.1 – 12 = 0
2x2 – 2xy + 3y2 + 2x \(\frac{(x+2 y)}{k}\) – y \(\frac{(x+2 y)}{k}\) – \(\frac{(x+2 y)^2}{k^2}\) = 0
k2 తో గుణించగా
2k2x2 – 2k2xy + 3k2y2 + 2kx (x + 2y) – ky (x + 2y) – (x + 2y)2 = 0
2k2x2 – 2k2xy + 3k2y2 + 2kx2 + 4kxy – kxy – 2ky2 – x2 – 4xy – 4y2 = 0
(2k2 + 2k – 1) x2 + (- 2k2 + 3k – 4) xy + (3k2 – 2k – 4) y2 = 0
OA, OB లు లంబంగా ఉన్నాయి కనుక
x2 గుణకం + y2 గుణకం 0.
2k2 + 2k – 1 + 3k2 – 2k – 4 = 0
5k2 = 5 ⇒ k2 = 1
∴ k = ±1
![]()
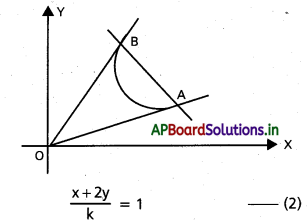
ప్రశ్న 3.
3x – y + 1 = 0 అనే రేఖ x2 + 2xy + y2 + 2x + 2y – 5 = 0 అనే వక్రాన్ని ఖండించే బిందువులను మూలబిందువుకు కలిపితే వచ్చే రేఖల మధ్యకోణాన్ని కనుక్కోండి. [Mar. ’13, ’07; May ’11; June ’04]
సాధన:
వక్రం సమీకరణం
x2 + 2xy + y2 + 2x + 2y – 5 = 0 ……………… (1)
AB సమీకరణము 3x – y + 1 = 0
y – 3x = 1 ……………….. (2)
(2) సహాయంతో (1) ని సమఘాత పరిస్తే OA, OB ల
ఉమ్మడి సమీకరణం
x2 + 2xy + y2 + 2x.1 + 2y.1 – 5.12 = 0
x2 + 2xy + y2 + 2x (y – 3x) + 2y (y – 3x) − 5 (y – 3x)2 = 0
x2 + 2xy + y2 + 2xy – 6x2 + 2y2 – 6xy – 5(y2 + 9x2 – 6xy) = 0
-5x2 – 2xy + 3y2 – 5y2 – 45x2 + 30 xy = 0
-50x2+ 28xy – 2y2 = 0
i.e, 25x2 – 14xy + y2 = 0
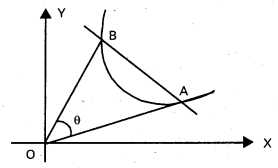
OA, OB ల మధ్య కోణము θ అనుకొందాం.
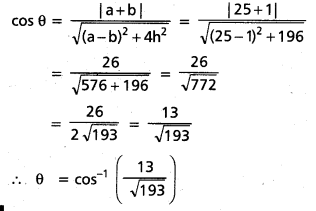
![]()
III.
ప్రశ్న 1.
మూలబిందువు కేంద్రంగా గల వృత్తం x2 + y2 = a2 కు lx + my = 1 అనేది ఒక జ్యా. ఈ జ్యా మూలబిందువు వద్ద లంబకోణం చేయడానికి నియమాన్ని కనుక్కోండి. [Mar. ’14, May ’13]
సాధన:
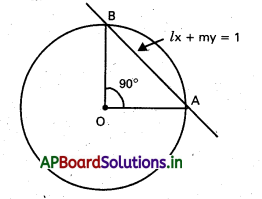
వృత్త సమీకరణము x2 + y2 = a2 ……………….. (1)
AB సమీకరణము lx + my = 1 ……………….. (2)
(2) సహాయంతో (1) ని సమఘాతపరిస్తే OA, OBల ఉమ్మడి సమీకరణం
x2 + y2 = a2 . 12
x2 + y2 = a2 (lx + my)2
= a2(l2x2 + m2y2 + 2lmxy)
= a2l2x2 + a2m2y2 + 2a2lmxy
i.e., a2l2x2 + 2a2 lmxy + a2 m2y2 – x2 – y2 = 0
(a2l2 – 1) x2 + 2a2 lmxy + (a2m2 – 1) y2 = 0
OA, OB లు లంబాలు కనుక
x2 గుణకం + y2 గుణకం = 0
a2 l2 – 1 + a2m2 – 1 = 0
a2(l2 + m2) = 2
ఇది కావలసిన నియమము.
![]()
ప్రశ్న 2.
lx + my = 1 అనే రేఖ x2 + y2 = a2 అనే వృత్తాన్ని ఖండించే బిందువులను మూలబిందువుకు కలిపితే వచ్చే రేఖలు ఏకీభవించడానికి నియమం కనుక్కోండి.
సాధన:
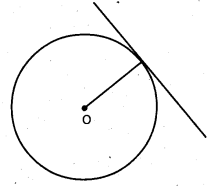
వృత్త సమీకరణము x2 + y2 = a2 …………….. (1)
AB సమీకరణము lx + my = 1 ………………… (2)
(2) సహాయంతో (1) ని సమఘాతపరిస్తే OA, OB ల ఉమ్మడి సమీకరణం.
x2 + y2 = a2 . 12
= a2 (lx + my) 2
= a2(l2x2 + m2y2 + 2lmxy)
i.e., x2 + y2 · a2l2x2 + a2 m2y2 + 2a2lmxy
(a2l2 – 1) x2 + 2a2lmxy + (a2m2 – 1) y2 = 0
OA, OB లు వక్రీభవిస్తున్నాయి.
⇒ h2 = ab
a4 l2m2 = (a2 l2 – 1)(a2m2 – 1)
a4 l2m2 = a4 l2m2 – a2 l2 – a2 m2 + 1
∴ a2 l2 – a2m2 + 1 = 0
a2 (l2 + m2) = 1
ఇది కావలసిన నియమము.
![]()
ప్రశ్న 3.
6x − y + 8 = 0 అనే రేఖ 3x2 + 4xy – 4y2 – 11x + 2y + 6 = 0 అనే సరళరేఖాయుగ్మాన్ని ఖండించే బిందువులను మూలబిందువుకు కలిపితే వచ్చే రేఖలు నిరూపకాక్షాలతో సమానకోణాలు చేస్తాయని చూపండి.
సాధన:
దత్త రేఖాయుగ్మం
3x2 + 4xy – 4y2 – 11 x + 2y + 6 = 0 ……………… (1)
దత్త రేఖ సమీకరణము
6x – y + 8 = 0 ⇒ \(\frac{6 x-y}{-8}\) = 1
⇒ \(\frac{y-6 x}{8}\) = 1
(2) సహాయంతో (1) ని సమఘాతపరచగా
3x2 + 4xy – 4y2 – (11x – 2y) \(\left(\frac{y-6 x}{8}\right)\) + 6 \(\left(\frac{y-6 x}{8}\right)^2\) = 0
= 64 [3x2 + 4xy – 4y2] – 8[11xy – 66x2 – 2y2 + 12xy] + 6[y2 + 36x2 – 12xy] = 0
936x2 + 256 xy – 256 xy – 234y2 = 0
∴ 468 x2 – 117 y2 = 0
⇒ 4x2 – y2 = 0
ఖండన బిందువులను మూలబిందువుకు కలిపే రేఖాయుగ్మ సమీకరణం
(3) యొక్క కోణ సమద్విఖండన రేఖల సమీకరణాలు
h(x2 – y2) – (a – b) xy = 0
0 (x2 – y ) – (4 – 1) xy = 0
⇒ xy = 0
x = 0 లేదా y
= 0 [నిరూపకాక్షాల సమీకరణాలు]
∴ దత్త రేఖల నిరూపకాక్షాల సమాన నిమ్నత కలిగి ఉన్నాయి.