AP Inter 1st Year Maths 1B Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Ex 8(c)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Exercise 8(c) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Exercise 8(c)

అభ్యాసం – 8 (సి)

I. క్రింద అవధులను గణించండి.

ప్రశ్న 1.

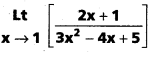
సాధన:

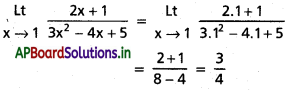
ప్రశ్న 2.

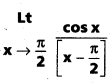
సాధన:
y = x – \(\frac{\pi}{2}\) అయితే x → \(\frac{\pi}{2}\) అయినప్పుడు y → 0 అవుతాయి

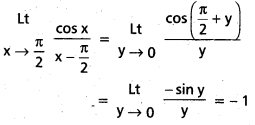
ప్రశ్న 3.
\(\stackrel{L t}{x \rightarrow 0}\frac{\sin a x}{x \cos x}\)
సాధన:

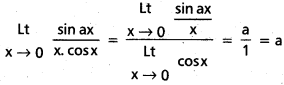
ప్రశ్న 4.
\(\stackrel{L t}{x \rightarrow 1}\frac{\sin (x-1)}{\left(x^2-1\right)}\)
సాధన:

ప్రశ్న 5.
\(\stackrel{L t}{x \rightarrow 0}\frac{\sin (a+b x)-\sin (a-b x)}{x}\)
సాధన:

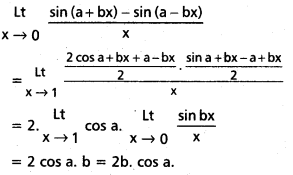
ప్రశ్న 6.
\(\stackrel{L t}{x \rightarrow a}\frac{\tan (x-a)}{x^2-a^2}\) (a ≠ 0) [T.S. Mar. ’15]
సాధన:
\(\stackrel{L t}{x \rightarrow a}\frac{\tan (x-a)}{x^2-a^2}\)
x = a + h అనుకొందాం x → a అయినప్పుడు h → 0 అవుతాయి.

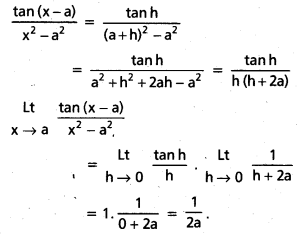
ప్రశ్న 7.
\(\stackrel{L t}{x \rightarrow 0}\frac{e^{7 x}-1}{x}\) [May. ’13]
సాధన:
x → 0 కావున
7x → 0

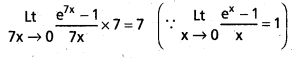
ప్రశ్న 8.
\(\stackrel{L t}{x \rightarrow 0}\frac{e^{3+x}-e^3}{x}\)
సాధన:
e³ \(\stackrel{L t}{x \rightarrow 0}\frac{e^{\mathrm{x}}-1}{\mathrm{x}}\)
= e³(1) = e³

ప్రశ్న 9.
\(\stackrel{L t}{x \rightarrow 0}\frac{e^x-e^3}{x-3}\)
సాధన:

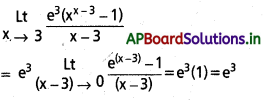
ప్రశ్న 10.
\(\stackrel{L t}{x \rightarrow 0}\frac{e^{\sin x}-1}{x}\)
సాధన:

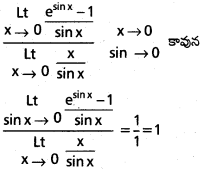
II.

ప్రశ్న 1.
\(\stackrel{L t}{x \rightarrow 1}\frac{(2 x-1)(\sqrt{x}-1)}{\left(2 x^2+x-3\right)}\)
సాధన:

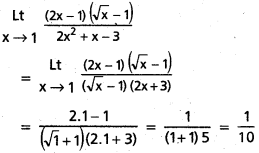
ప్రశ్న 2.
\(\stackrel{L t}{x \rightarrow a}\left[\frac{x \sin a-a \sin x}{x-a}\right]\) [Mar. ’11]
సాధన:


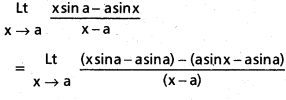
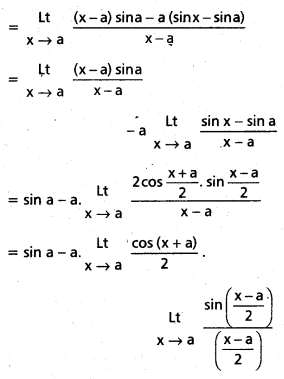
= sin a – a cos a . 1 = sin a – a cos a

ప్రశ్న 3.
\(\stackrel{L t}{x \rightarrow 0}\left[\frac{\cos a x-\cos b x}{x^2}\right]\) [May ’11]
సాధన:

ప్రశ్న 4.
\(\stackrel{L t}{x \rightarrow 2}\frac{\left(2 x^2-7 x-4\right)}{(2 x-1)(\sqrt{x}-2)}\)
సాధన:

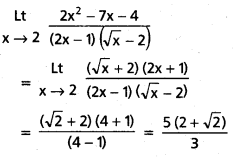
ప్రశ్న 5.
\(\stackrel{L t}{x \rightarrow 0}\frac{\log _e(1+5 x)}{x}\)
సాధన:
x → 0 కావున
5x → 0

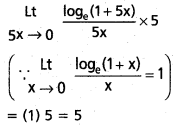
ప్రశ్న 6.

సాధన:
L.H. నియమం ప్రకారం

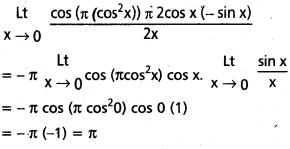
III.

ప్రశ్న 1.

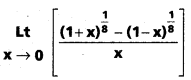
సాధన:

ప్రశ్న 2.
\(\stackrel{L t}{x \rightarrow 0}\left[\frac{3^x-1}{\sqrt{1+x}-1}\right]\)
సాధన:

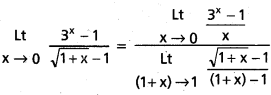
= \(\frac{\log 3}{\frac{1}{2} \cdot 1^{-\frac{1}{2}}}\) = (2 . log 3)

ప్రశ్న 3.
\(\stackrel{L t}{x \rightarrow a}\left[\frac{\sqrt{a+2 x}-\sqrt{3 x}}{\sqrt{3 a+x}-2 \sqrt{x}}\right]\)
సాధన:

ప్రశ్న 4.
\(\stackrel{L t}{x \rightarrow 0}\frac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}\)
సాధన:

ప్రశ్న 5.
\(\stackrel{L t}{x \rightarrow a}\frac{\sin (x-a) \tan ^2(x-a)}{\left(x^2-a^2\right)^2}\)
సాధన:

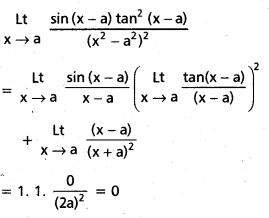
ప్రశ్న 6.
\(\stackrel{L t}{x \rightarrow 0}\frac{1-\cos 2 m x}{\sin ^2 n x}\) (m, n ∈ Z)
సాధన:

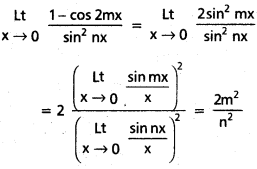
ప్రశ్న 7.
\(\stackrel{L t}{x \rightarrow 0}\frac{1-\cos x}{x}\)
సాధన:

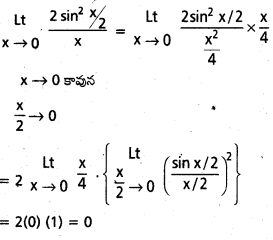
ప్రశ్న 8.
\(\stackrel{L t}{x \rightarrow 0}\frac{\sec x-1}{x^2}\)
సాధన:

ప్రశ్న 9.
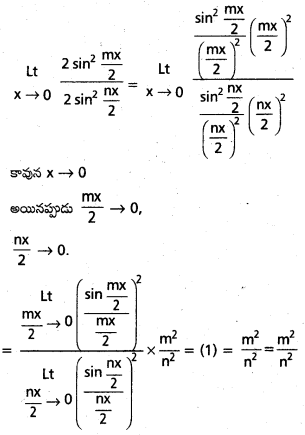
\(\stackrel{L t}{x \rightarrow 0}\frac{1-\cos m x}{1-\cos n x}\), (n ≠ 0)
సాధన:

ప్రశ్న 10.
\(\stackrel{L t}{x \rightarrow 0}\frac{x\left(e^x-1\right)}{1-\cos x}\)
సాధన:

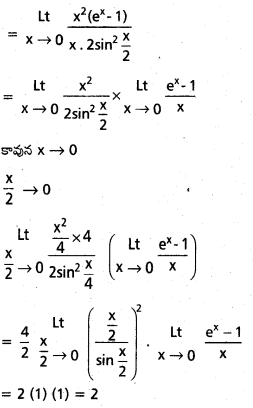
ప్రశ్న 11.
\(\stackrel{L t}{x \rightarrow 0}\frac{\log \left(1+x^3\right)}{\sin ^3 x}\)
సాధన:

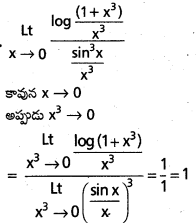
ప్రశ్న 12.
\(\stackrel{L t}{x \rightarrow 0}\frac{x \tan 2 x-2 x \tan x}{(1-\cos 2 x)^2}\)
సాధన: