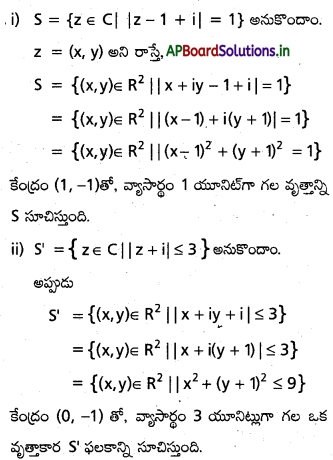AP Inter 2nd Year Maths 2A Important Questions Chapter 1 సంకీర్ణ సంఖ్యలు

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 1 సంకీర్ణ సంఖ్యలు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 1 సంకీర్ణ సంఖ్యలు

ప్రశ్న 1.
\(\frac{4+2 i}{1-2 i}+\frac{3+4 i}{2+3 i}\) ను a + ib, a, b ∈ R రూపంలో వ్యక్తపరచండి.
సాధన:

ప్రశ్న 2.
\(\frac{a+i b}{a-i b}\) సంకీర్ణ సంఖ్య వాస్తవ, కల్పిత భాగాలను కనుక్కోండి.
సాధన:

ప్రశ్న 3.
(1-i)³(1+i) ను a+ib రూపంలో వ్యక్తపరచండి.
సాధన:
(1-i)³(1+i)=(1-i)²(1-i)(1+i)
=(1+i²-2i) (1²-i²)
=(1-1-2i)(1+1)
=0-4 i=0+i(-4)

ప్రశ్న 4.
7 + 24 i యొక్క గుణన విలోమాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 5.
Z ≠ 2i \(\left(\frac{z-4}{z-2 i}\right)\) వాస్తవ భాగం సున్న అయ్యే z బిందుపథాన్ని నిర్ణయించండి.
సాధన:

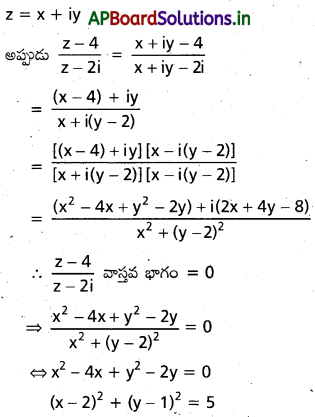
కాబట్టి z ≠ 2i అయి, \(\cdot\left(\frac{z-4}{z-2 i}\right)\) కు వాస్తవ భాగం =0 ⇔ (x, y) ≠ (0,2) మరియు (x-2)²+(y-1)²=5. కనుక దత్త సంకీర్ణ సంఖ్యను సూచించే దత్త బిందువు బిందు పథం (2,1) కేంద్రం \(\sqrt{5}\) వ్యాసార్థంతో (0,2) బిందువు మినహా ఒక వృత్తాన్ని సూచిస్తుంది.

ప్రశ్న 6.
x, y వాస్తవ సంఖ్యలవుతూ, 4 x+i(3 x-y)= 3 – 6i అయితే, x, y విలువలను కనుక్రోండి.
సాధన:
∴ 4 x+i(3 x-y)=3-6i
వాస్తవ, సంకీర్ణ భాగాలను పోలిస్తే,
4 x=3,3 x-y=-6
⇒ x=3/4

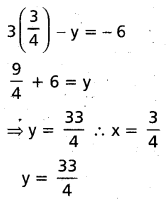
ప్రశ్న 7.
z=2-3 is, అయితే, z²-4 z+13=0 అని చూపండి.
సాధన:
∴ z=2-3i
z – 2 = – 3i
(z – 2)² = (- 3i)²
= z² –  4z + 4 = 9i²
z² – 4z + 4 = 9(-1)
z² – 4z + 13 = 0

ప్రశ్న 8.
(3 + 4i) (2 – 3i) కి సంకీర్ణ యుగ్మాన్ని కనుక్కోండి.
సాధన:
(3+4 i)(2-3i)=6+8i-9i-12i²
=6-i-12(-1)=18-i
దాని సంకీర్ణ సంయుగ్మం 18 +i

ప్రశ్న 9.
\(z_1=\frac{2+11 i}{25}, z_2=\frac{-2+i}{(1-2 i)^2}\) లు పరస్పరం సంయుగ్మాలని చూపండి.

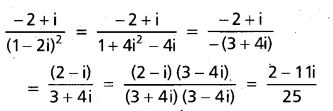
ఈ సంకీర్ణ సంఖ్య \(\frac{2+11 \mathrm{i}}{25}\) కు సంయుగ్మం, కాబట్టి దత్త సంకీర్ణ సంఖ్యలు z₁, z₂ లు రెండూ పరస్పర సంయుగ్మ సంకీర్ల సంఖ్యలు. (-5 + 12i) కి వర్గమూలాలను కనుక్కోండి.

ప్రశ్న 10.
(-5 + 12i) కి వర్గమూలాలను కనుక్కోండి.
సాధన:

ప్రశ్న 11.
\(z=-\sqrt{7}+i \sqrt{21}\) కు ద్రువరూపం
సాధన:

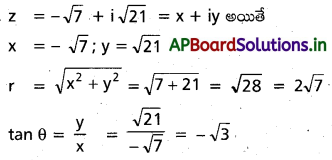
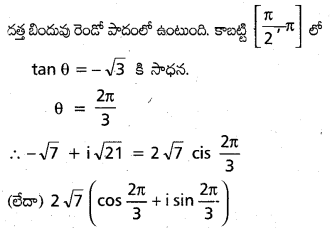
ప్రశ్న 12.
(-1 -i) ను (ప్రధాన ఆయామం విలువతో ధ్రువ రూపంలో వ్యక్తపరచండి.
సాధన:
-1-i=r(cos θ+i sin θ) అనుకోండి.
-1 =r cos θ
-1 =r sin θ
tan θ =1 ………………. (1)

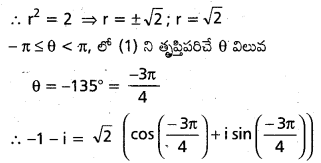
ప్రశ్న 13.
\(\left(\frac{z-2}{z-6 i}\right)\) ఆయామం \(\frac{\pi}{2}\) అయితే, బిందుపథం కనుక్కోండి.
సాధన:

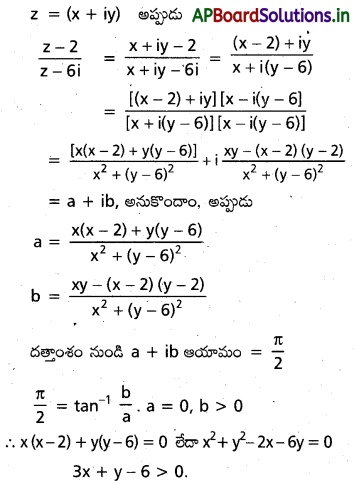
ప్రశ్న 14.
సంకీర్ణ తలంలోని ఏ వృత్త సమీకరణమైనా, \(\mathbf{z} \overline{\mathbf{z}}+\mathbf{b} \overline{\mathbf{z}}+\overline{\mathbf{b}} \mathbf{z}+\mathbf{c}=\mathbf{0}\) (b∈C, C∈R) రూపంలో ఉంటుందని చూపండి.
సాధన:
కార్టిషియన్ రూపంలో వృత్త సమీకరణం
x²+y²+2 gx+2 fy+c=0,
(g, f ∈ R) గా తీసుకొందాం. ………………. (1)
ఈ సమీకరణాన్ని సంకీర్ణ రూపంలో [వాయడానికి,(x,y) = z అనుకొందాం.

ప్రశ్న 15.
z²+ \(\bar{z}^2\) =2 ను తృప్తిపరిచే సంకీర్ణ సంఖ్య z లు, ఒక అతిపరావలయంగా ఏర్పడతాయని చూపండి.
సాధన:
\(z^2+\bar{z}^2\) =2 సమీకరణంలో z = x + iy (వరాస్తే, ఇచ్చిన సంకీర్ణ సంఖ్యకు కార్టిషియన్ రూపం వస్తుంది.
∴ (x+i y)²+(x-i y)²=2
i.e., x²-y²+2 ixy+x²-y² 2 ixy = 2
i.e., x²-y²=1 .
ఈ సమీకరణం ఒక అతిపరావలయంను సూచిస్తుంది.
\(\mathrm{z}^2+(\overline{\mathrm{z}})^2\) = 2 ని తృప్తిపరిచే సంకీర్ణ సంఖ్యలన్నీ
x²-y²=1 అనే అతిపరావలయంగా ఏర్పడతాయి.

ప్రశ్న 16.
ఆర్గాండ్ పటంలో 1+3 i, 4-3 i, 5 – 5i సంకీర్ణ సంఖ్యలను సూచించే బిందువులా సరేఖియాలని చూపండి.
సాధన:
ఇచ్చిన మూడు సంకీర్ణ సంఖ్యలని ఆర్గాండ్ పటంలో వరుసగా P, Q, R లతో సూచిద్దాం.
P=(1,3) ; Q=(4,-3) ; R=(5,-5)
P, Q లను కలిపే రేఖ వాలు = \(\frac{3+3}{1-4}=\frac{6}{-3}=-2\)
Q, R లను కలిపే రేఖ వాలు = \( \frac{-3+5}{4-5}=\frac{2}{-1}=-2\)
PQ వాలు, QR వాలుకు సమానం కనుక P, Q, R బిందువులు సరేఖియాలు.

ప్రశ్న 17.
ఆర్గాండ్ తలంలో (-4+3 i),(2-3 i) లను సూచించే బిందువులను కలిపే సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
దత్త ఐిందువులను
A=-4+3 i=(-4,3),
B=2-3 i=(2,-3) గా తీసుకుందాం,
సరళరేఖ \(\stackrel{\leftrightarrow}{AB}\) సమీకరణం
y-3= \(\frac{3+3}{-4-2}(x+4)\)
i.e., x+y+1=0

ప్రశ్న 18.
ఆర్గాండ్ తలంలో z=x+1 y ఒక బిందువును సూచిస్తుంది. |z|=2 అయ్యేటట్లు z బిందుపథాన్ని కనుక్రోండి.
సాధన:
|z|=2
z= x+iy  అనుకొందాం.
|x+iy|=2
⇔ \(\sqrt{x^2+y^2}\) =2 ⇔ x²+y²=4
x²+y²=4 సమీకరణం, కేంద్రం (0,0) గా 2 యానిట్లు
వ్యాసార్థంగా గల వృత్తాన్ని సూచిస్తుంది.
∴ |z|=2 కు బిందుపథం x² +y² =4 అనే వృత్తం.

ప్రశ్న 19.
ఆర్గాండ్ తలంలో p బిందువు, సంకీర్ణసంఖ్ల z ను సూచిస్తుంది. z అయామం \(\frac{\pi}{4}\) అయితే P బిందకపథాన్ని నర్ణయించండ.
సాధన:
z=x+i y అనుకొందాం.
z కు ఆయామం \(\frac{\pi}{4}\)
i.e., \(\tan ^{-1}\left(\frac{y}{x}\right)=\frac{\pi}{4}\)
\(\frac{y}{x}=\tan \frac{\pi}{4}=1\)
x=y
∴P  బిందుపథం x = y

ప్రశ్న 20.
ఆర్గాండ్ సమతలంలో P బిందువు సంకీర్ణ సంఖ్య z=x+i y ను సూచించినప్పండు \(\frac{z-i}{z-1}\) శుద్ధకల్పిత సంఖ్య అయీతే, P బిందుపథాన్ని కననుక్రోండి.
సాధన:
z=1 అయితే \(\frac{z-i}{z-1}\) నిర్వచితం కాదు.

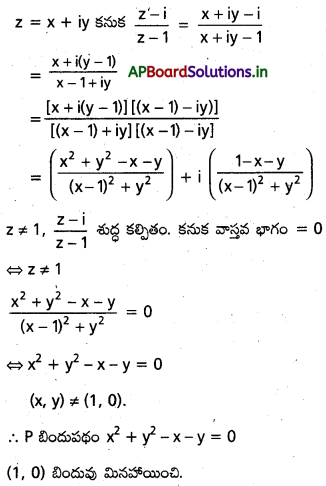
ప్రశ్న 21.
(కింది ఉదహరించిన C యెకక్క ఉపసమితులను, జ్యామితీయంగా వివరించండి.
(i) { z∈C| | z – 1+ i| = 1}
(ii) { z∈C | | z+i| ≤ 3}
సాధన: