AP Inter 2nd Year Maths 2A Important Questions Chapter 8 విస్తరణ కొలతలు

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 8 విస్తరణ కొలతలు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 8 విస్తరణ కొలతలు

ప్రశ్న 1.
అవర్గీకృత దత్తాంశము 6, 7, 10, 12, 13, 4, 12, 16 నకు డుధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.
సాధన:
దత్తాంశానికి అంకమధ్యమం.

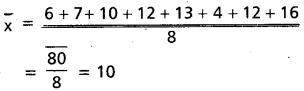
ప్రశ్న 2.
అవర్గీకృత దత్తాంశము 6, 7, 10, 12, 13, 4, 12, 16 నకు మధ్యగతం నుంచి మధ్యమ విచలనాన్ని గణించండి.
సాధన:
దత్తబిందువులను పరిమాణం పరంగా ఆరోహణక్రమంలో (వాయగా 4, 6, 7, 10, 12, 12, 13, 16
∴ మధ్యగతం = \(\frac{10+12}{2} = 11\)
పరమ మూల్ల విలువలు
|11-4|, |11-6|, |11-7|, |11-10|, |11-12|, |11-12|, |11-13|, |11-16|
= 7, 5, 4, 1, 1, 1, 2, 5
∴ మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{1}{8}\) (7+5+4+1+1+1+2+5)
= \(\frac{26}{8}\) = 3.25

ప్రశ్న 3.
క్రింది దత్తాంశానికి మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.

సాధన:

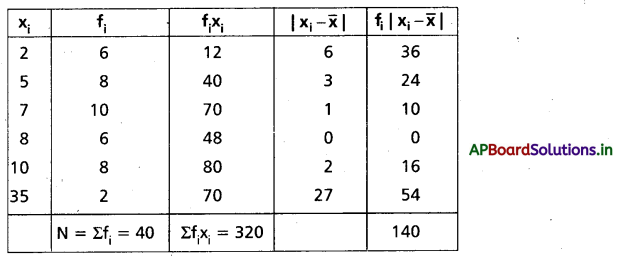
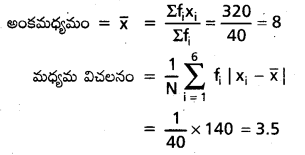
ప్రశ్న 4.
క్రింది దత్తాంశానికి మధ్యగతం నుంచి మధ్యమ విచలనం కనుగొనుము.

సాధన:

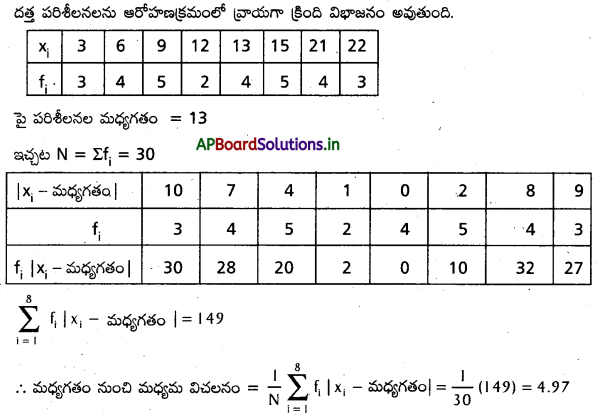
ప్రశ్న 5.
ఇచ్చిన దత్తాంశానికి మద్యమం నుంచి మధ్యమ విచలనం కనుగొనుము.

సాధన:

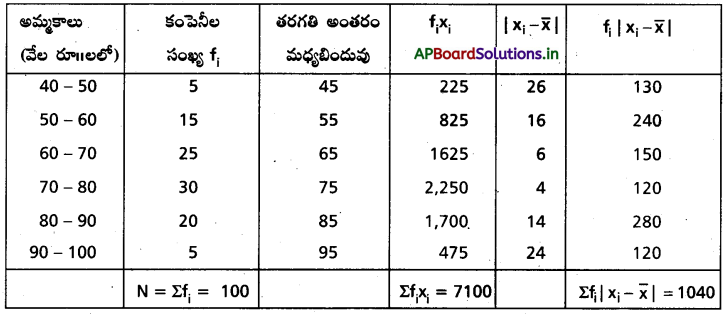
ప్రశ్న 6.
క్రింది దత్తాంశానికి, మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.

సాధన:

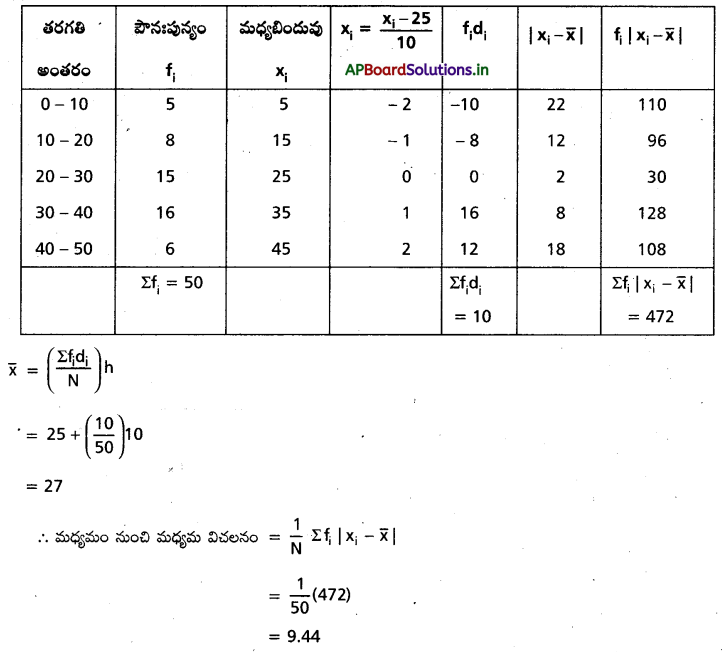
ప్రశ్న 7.
క్రింది దత్తాయాానికి మధ్యగతం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.

సాధన:

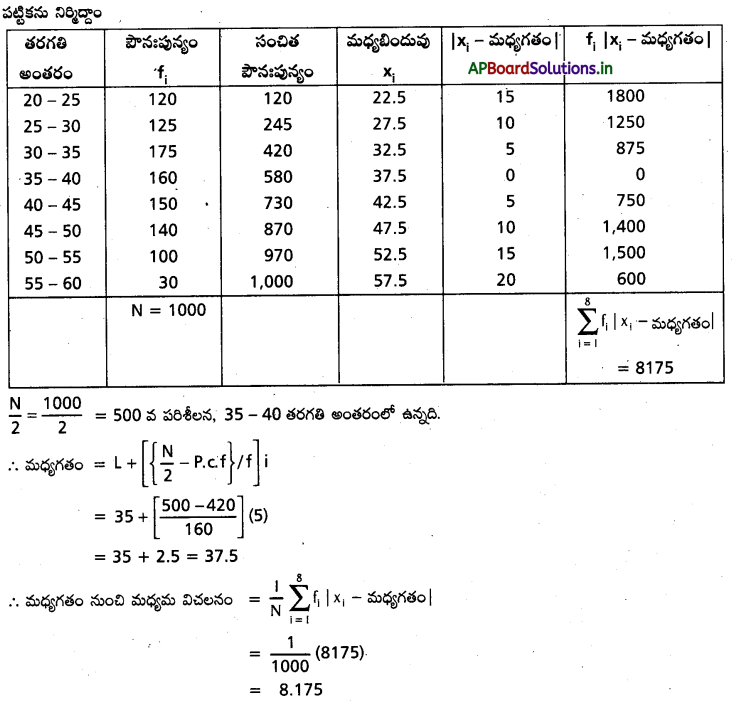
ప్రశ్న 8.
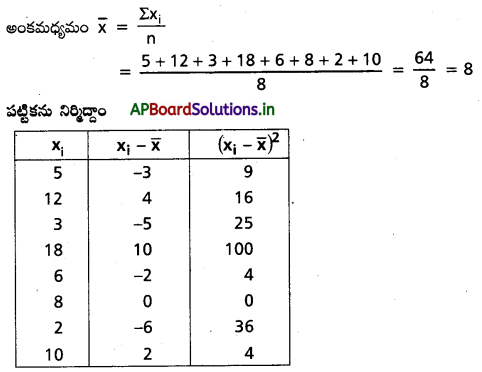
క్రింది దత్తాంశానికి విస్తృతి, (ప్రామాణిక విచలనాలను కనుగొనుము 5,12,3,18,6,8,2,10
సాధన:

ప్రశ్న 9.
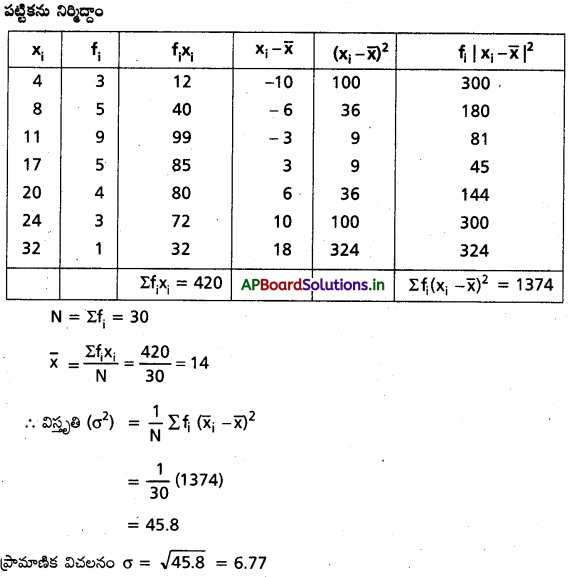
క్రింది దత్తాంశానికి విస్తృతి మరియు (ప్రామాణిక విచలనాన్ని కనుగొనుము.

సాధన:

ప్రశ్న 10.
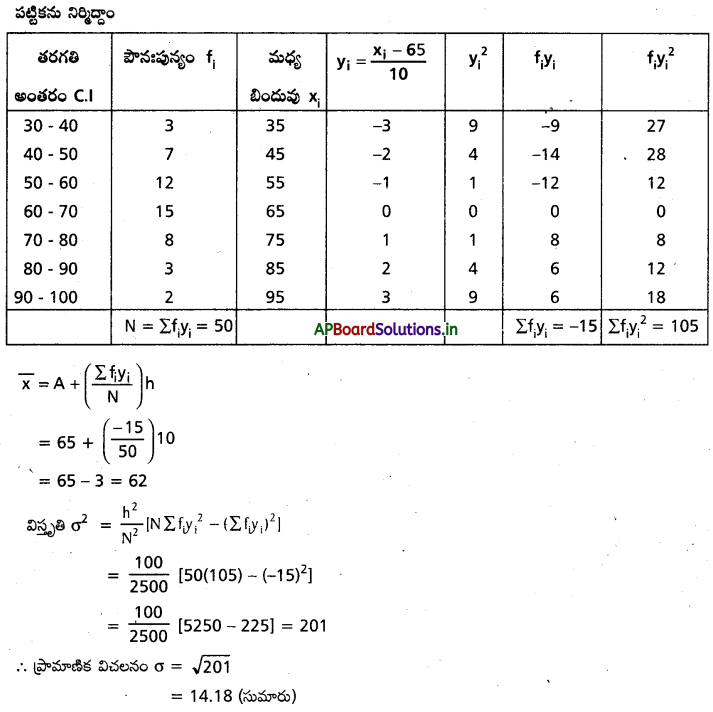
ఈ క్రింది అవిచ్ఛిన్న పౌనఃపున్య విాజనానికి విస్తృతి ప్రామాణిక విచలనాన్ని గణించండి.

సాధన:
ఉహత్మక మధ్యమం A = 65 అనుకొనుము
అపుడు  \(y_i=\frac{x_i-65}{10}\)

ప్రశ్న 11.
ఒక తరగతికి చెందిన రెండు విభాగాలు A, B లలోని విద్యార్థులు, 100 మార్కులకు పెట్టిన ఒక పరీక్షలో క్రింది ఫలితాలను సాధించారు. వీరిలో ఏ విభాగంలోని విద్యార్థులు, వారి ఫలితాలలో ఎక్కువ విచలనాన్ని కలిగి ఉన్నారో కనుగొనుము.

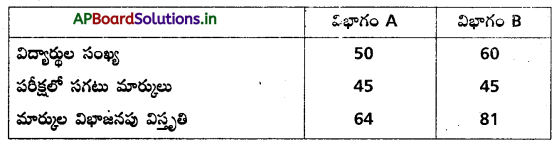
సాధన:
విభాగం – A విద్యార్ధుల మార్కుల విభాజన విస్తృతి σ²₁ = 81
⇒ ప్రామాణిక విచలనం σ₁ =8
విభాగం – B విద్యార్థుల మార్కుల విభాజన విస్తృతి σ²₂ = 81
⇒ σ₂ = 9
రెండు విభాగాలలోని విద్యార్థుల సగటు మార్కులు ఒకటి (అంటి 45) కావున అధిక ప్రామాణిక విచలనం కలిగిన విభాగం ఎక్కువ విచలనాన్ని కలిగి ఉంటుంది.
∴ విభాగం B వారి పనితనం అధిక విచలనాన్ని కలిగి ఉంటుంది.

ప్రశ్న 12.
ఒక సర్వేలో రాబట్టిన రెండు నమూనాల రఫ్రిజిరేటర్లు A, B ల మన్నిక కాలం ఈ క్రింది పట్టికలో ఇవ్వడమైనది. మీరు ఏ నమూనా రిఫ్రిజిరేటరును కొనవచ్చని సూచిస్తారు.

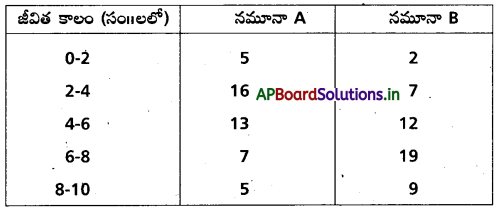
సాధన:
నమూనా A, నమూనా B రి్రిజిరేటర్ల మన్నిక కాలాలు మధ్యమం, విస్తృలిలను కనుక్కొవడానికి పట్టికను నిర్మిద్దాం.

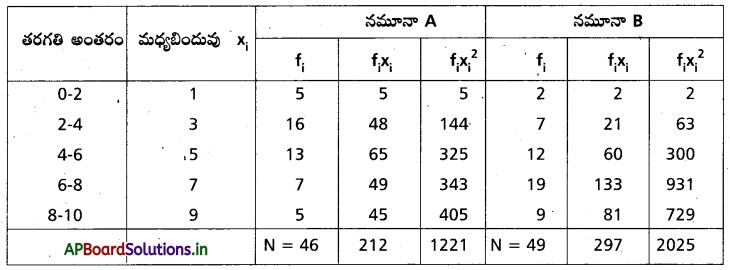
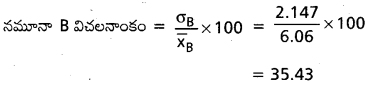
నమూనా B విచలనాంకం నమూనా A విచలనాంకం కంటే తక్కువగా ఉన్నది.
నమూనా B కొనవచ్చునని సూచిస్తాం.

ప్రశ్న 13.
సోపాన విచలన పద్ధతిని ఉపయోగించి, (క్ంిది దత్తాంశానికి మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుగొనుము.

సాధన:
ఉహత్మక మధ్యమం A = 35

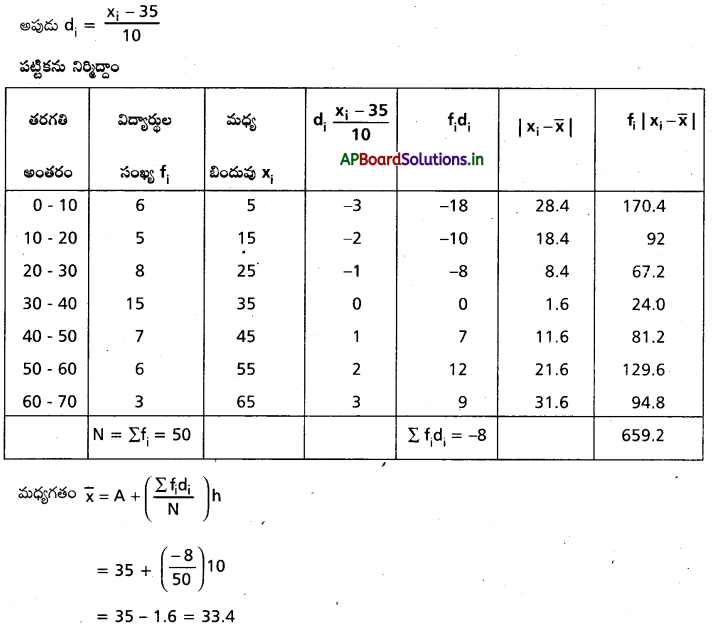
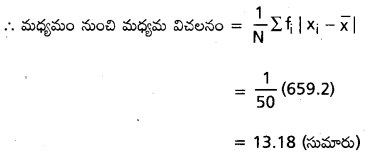
ప్రశ్న 14.
ఈ క్రింది పట్టిక, ఒక కర్మాగారంలో పనివాళ్ళ రోజు వారీ జీతాలను తెలుపుతుంది.ఈ పనివాళ్ళ జీతాల ప్రామాణిక విచలనాన్ని, విచలనాంకంను గణనం చేయండి.

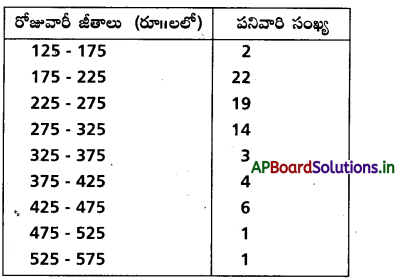
సాధన:
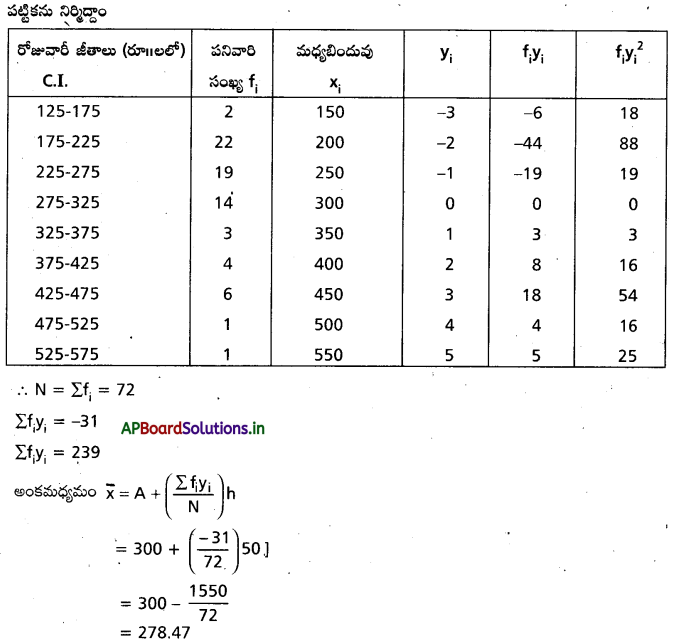
తరగతి అంతరాల మధ్యబిందువులు సంఖ్యాపరంగా పెద్దవి కనుక ఈ సమస్యను సోపాన విచలన పద్ధతినుపయోగించి సాధిస్తాము.
ఇక్కడ h=50
ఊహత్మక మధ్యమం A=300
అపుడు \( y_i=\frac{x_i-300}{50}\)

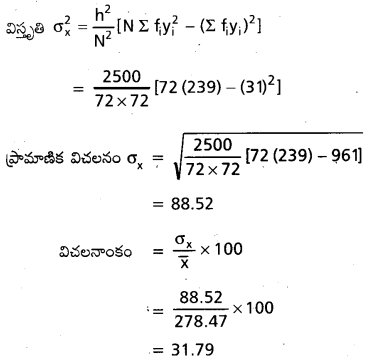
ప్రశ్న 15.
ఒకే రకం పంర్రమకు చెందిన .రండు సంస్థల A, Bలలోని పనివారికి ఇచ్చిన జీతాలను విశ్లేషణ చేసినప్పుడు ఈ క్రింది పట్టికలోని వివరాలు తెలిసాయి.

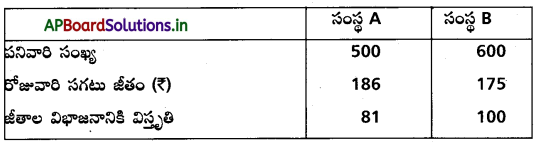
i) A లేదా B లో ఏ సంస్థ, ఆ పరిశ్రమలోని జీతాలలో ఎక్కువ విచరణ కలిగి ఉంది ?
ii) ఏ సంస్థ ఎక్కువ జీతం బిల్లును కలిగి ఉంది ?
సాధన:
i) ఇచ్చిన σ²_A= 81 ⇒ σ_A= 9
σ²_B = 100 ⇒ σ_B= 10
\(\bar{x}_A\) = 186 మరియు \(\bar{x}_B\) = 175
సంస్థ A జీతాల విభాజనపు విచలనాంకం = \(\frac{\sigma_A}{x_A} \times 100=\frac{9}{186} \times 100=4.84\)
సంస్థ B జీతాల విభాజనపు విచలనాంకం = \(\frac{\sigma_{\mathrm{B}}}{\mathrm{x}_{\mathrm{B}}} \times 100=\frac{10}{175} \times 100=5.71\)
∴ సంస్థ B కి విచలనాంకం, సంస్థ A విచలనాంకం పెద్దది కనుక, వ్యక్తిగత జీతాలకి సంబంధించి, సంస్థ B ఎక్కువ విచలనాన్ని కలిగినదని చెప్పగలం.

ii) సంస్థ A లోని పనివారికి చెల్లించిన మొత్తం జీతాలు= 500 ×186 = 93,000
సంస్థ B లోని పనివారికి చెల్లించిన మొత్తం జీతాలు =600 ×175 = 1,05,000
∴ సంస్థ B కి ఎక్కువ జీతం బిల్లు కలదని చెప్పవచ్చును.

ప్రశ్న 16.
20 పరిశీలనల విస్తృతి 5. (పతి పరిశీలసను 2 చే గుణించినప్పుడు వచ్చే పరిశీలనల విస్తృ)తిని కనుగొనుము.
సాధన:
దత్తపరిశీలనలను x₁, x₂,……………….. x₂₀ వాటి మధ్యమం \(\overline{\bar{x}}\) అనుకొనుము.
దత్తాంశం నుంచి n=20 మరియు విస్తృతతి = 5

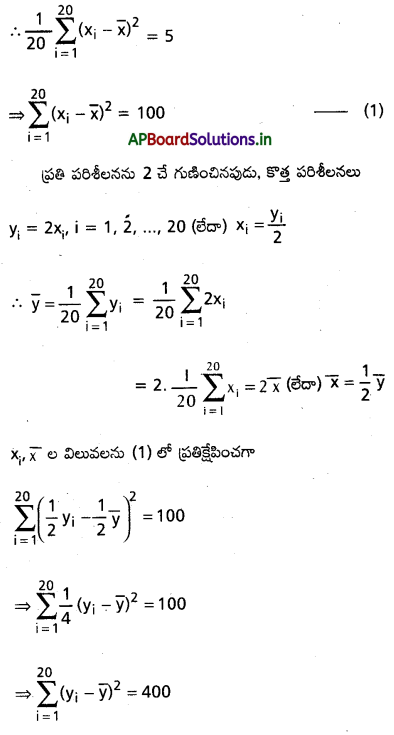
∴ ఫలితంగా వచ్బే పరిశీలన విస్త్లృతి = \(\frac{1}{20}\) × 400 = 20 = 2² × 5

ప్రశ్న 17.
పరిశీలన x₁, x₂ ……………………….. x_n లలో (ప్రతిదాన్ని k కి పెంచితే లేదా కలిపితే (k ఒక ధనాత్మక లేదా రుణాత్మక సంఖ్య), వచ్చే పరిశీలనల విస్తృతి ఏమి మారదని చూపండి.
సాధన:
x₁, x₂ ……………………….. x_n ల మధ్యమం x అనుకొందాం.
అప్పుడు వాటి నిస్తృతి \(\sigma_1^2=\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \)
ప్రతి పరిశీలనకు ఒక స్థిరరాశి k కలిపితే, వచ్చే కొత్త పరిశీలనలు y_i = x_i + k ………………. (1)

ప్రశ్న 18.
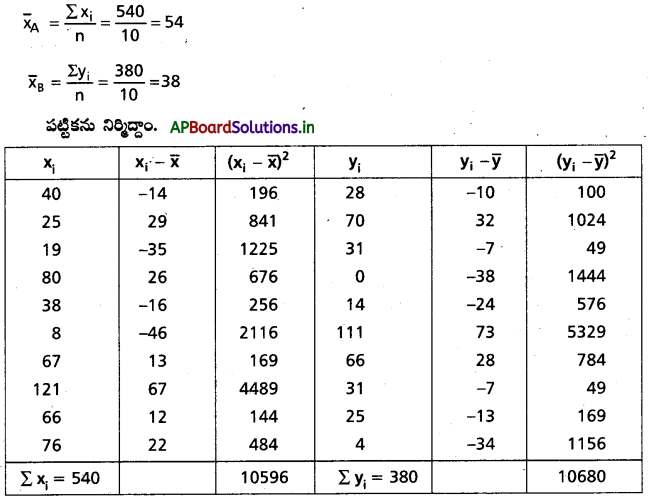
10 ఇన్నింగులలో A, Bఅనే ఇద్దరు క్రికెట్ అటగాళ్ళు స్కోరులు ఈ క్రింద ఇవ్వడమైనది. వీరిలో ఎక్కువ పరుగులు సాధించిన ఆటగాడో, ఎవరు ఎక్కువ నిలకడగల అటగాడో కనుగానుము.

సాధన: