AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Ex 1(c)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 1 వృత్తం Exercise 1(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Exercise 1(c)

అభ్యాసం – 1(సి)

I.

ప్రశ్న 1.
కింద ఇచ్చిన ప్రతి S = 0 వృత్తానికి P వద్ద స్పర్శరేఖ సమీకరణాన్ని కనుక్కోండి.
i) S ≡ x² + y² – 6x + 4y – 12; P = (7, -5)
సాధన:
వృత్త సమీకరణము
S ≡ x² + y² – 6x + 4y – 12 = 0
P(7, -5) వద్ద స్పర్శరేఖ సమీకరణము
S₁ = xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x. 7 + y(-5) – 3(x + 7) + 2(y −5) – 12 = 0
⇒ 7x – 5y – 3x – 21 + 2y – 10 – 12 = 0
4x – 3y – 43 = 0

ii) S ≡ x² + y²-6x + 4y – 12; P = (-1, 1)
సాధన:
P వద్ద స్పర్శరేఖ సమీకరణము
x(-1) + y. 1 – 3(x – 1) + 2(y + 1) – 12 = 0
⇒ -x + y – 3x + 3 + 2y + 2 – 12 = 0
⇒ – 4x + 3y – 7 = 0
4x – 3y + 7 = 0

iii) S ≡ x² + y² + 4x + 6y – 39; P= (-6, -9)
సాధన:
P వద్ద స్పర్శరేఖ సమీకరణము S₁ = 0
(i.e.,) x(-6) +y(-9) +2(x – 6) + 3(y – 9) – 39 = 0
⇒ -6x – 9y + 2x – 12 + 3y – 27 – 39 = 0
⇒ -4x – 6y – 78 = 0
⇒ 4x + 6y + 78 = 0
⇒ 2x + 3y+ 39 = 0

iv) S ≡ x² + y² – 4x – 6y + 11; P = (3, 4)
సాధన:
P వద్ద స్పర్శరేఖ సమీకరణము S₁ = 0
⇒ x(3) + y(4) – 2(x + 3) – 3(y + 4) + 11 = 0
3x + 4y – 2x – 6 – 3y – 12 + 11 = 0
x + y – 7 = 0

ప్రశ్న 2.
కింద ఇచ్చిన ప్రతి S = 0 వృత్తానికి P వద్ద అభిలంబ రేఖ సమీకరణాన్ని కనుక్కోండి.
i) S ≡ x² + y² + x + y – 24; P = (3,-4)
సాధన:
అభిలంబరేఖ సమీకరణము
(x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
(x -3) (- 4 + \(\frac{1}{2}\)) – (y + 4) (3 + \(\frac{1}{2}\)) = 0
–\(\frac{7}{2}\)(x – 3) – \(\frac{7}{2}\) (y + 4) = 0
⇒ (x – 3) + (y + 4)
x – 3 + y + 4 = 0
x + y + 1 = 0

ii) S ≡ x² + y² – 10x – 2y + 6; P = (3, 5)
సాధన:
అభిలంబ రేఖ సమీకరణము
(x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
(x – 3) (5 – 1) – (y – 5) (3 – 5) = 0
4x – 12 + 2y – 10 = 0
4x + 2y – 22 = 0
లేదా
2x + y – 11 = 0

iii) S ≡ 3(x² + y²) – 19x – 29y + 76; P = (1,3)
సాధన:
వృత్త సమీకరణము
x² + y² – \(\frac{19}{3}\)x – \(\frac{29}{3}\) y + \(\frac{76}{3}\) = 0
(x – 1) (3 – \(\frac{29}{3}\)) – (y – 3) (1 – \(\frac{19}{6}\)) = 0
– \(\frac{11}{6}\) (x – 1) + \(\frac{13}{6}\) (y – 3) = 0
11(x – 1) – 13(y – 3) = 0
11x – 11 – 13y + 39 = 0
11x – 13y + 28 = 0

iv) S ≡ x² + y² – 22x – 4y + 25; P = (1, 2)
సాధన:
P వద్ద అభిలంబరేఖ సమీకరణము
(x – 1) (2 – 2) – (y – 2) (1 – 11) = 0
10(y – 2) = 0 ⇒ y – 2 = 0
లేదా y = 2

II.

ప్రశ్న 1.
x² + y² −x + 3y – 22 = 0 y=x -3 రేఖపై ఏర్పరచే జ్యా పొడవును కనుక్కోంది. (Mar.’13, May ’11)
సాధన:
వృత్త సమీకరణము
S = x² + y² – x + 3y – 22 = 0

= \(\sqrt{96}=4 \sqrt{6}\) యూనిట్లు.

ప్రశ్న 2.
x²+ y² – 8x – 2y – 80 వృత్తం x + y + 1 = 0 రేఖపై ఏర్పరచే జ్యా పొడవును కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
వృత్త సమీకరణము x + y – 8x – 2y – 8 = 0
కేంద్రం C(4, 1), r = \(\sqrt{16+1+8}\) = 5
రేఖ సమీకరణము x + y + 1 = 0
P = కేంద్రం నుండి లంబ దూరము = \(\frac{|4+1+1|}{\sqrt{1+1}}\)
= \(\frac{6}{\sqrt{2}}=3 \sqrt{2}\)
జ్యా పొడవు = 2 \(\sqrt{r^2-p^2}\)
= 2\(\sqrt{25-18}\)
= 2\(\sqrt{7}\) యూనిట్లు.

ప్రశ్న 3.
x² + y² = a² వృత్తం x cos α + y sin α = p రేఖపై ఏర్పరచే జ్యా పొడవును కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y² = a²
కేంద్రం C(0, 0), r = a
రేఖ సమీకరణము
x cos α + y sin α – P = 0
P = కేంద్రం నుండి లంబ దూరము
\(\frac{|0+0-p|}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\) = p
జ్యా పొడవు = 2\(\sqrt{a^2-p^2}\)

ప్రశ్న 4.
(2, 3) కేంద్రంగా ఉంటూ 3x – 4y + 1 =0 రేఖను స్పృశించే వృత్త సమీకరణాన్ని కురుక్కోండి.
సాధన:

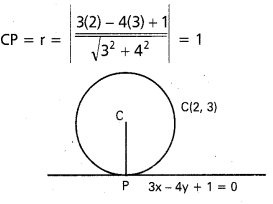
వృత్త సమీకరణము (x – h)² + (y – k)² = r²
(x – 2)² + (y – 3)² = 1
x² + y² – 4x – 6y + 12 = 0

ప్రశ్న 5.
(-3, 4) కేంద్రంగా ఉంటూ Y – అక్షాన్ని స్పృశించే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:

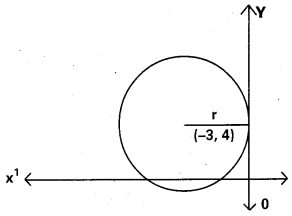
కేంద్రం C (-3, 4)
వృత్తం Y – అక్షాన్ని స్పృశిస్తుంది.
r యొక్క X నిరూపకం C = |-3 = 3
వృత్త సమీకరణము (x + 3)² + (y – 4)² = 9
x² + 6x + 9 + y² – 8y + 16 – 9 = 0
x² + y² + 6x – 8y + 16 = 0

ప్రశ్న 6.
x² + y² – + y − 8x − 2y + 12 = 0 వృత్తానికి y నిరూపకం 1 అయ్యే బిందువుల వద్ద స్పర్శరేఖ సమీకరణాలను కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
x² + y² – 8x – 2y + 12 = 0
P నిరూపకాలు (X,, 1) అనుకొందాం.
P వృత్తం మీది బిందువు
x₁² + 1 – 8x₁ – 2 + 12 = 0
x₁²– 8x₁ + 11 = 0
x₁ = \(\frac{8 \pm \sqrt{64-44}}{2}=\frac{8 \pm 2 \sqrt{5}}{2}=4 \pm \sqrt{5}\)
x₁ = 4 + \(\sqrt{5}\), x₂ = 4 – \(\sqrt{5}\)
P నిరూపకాలు (4 + \(\sqrt{5}\), 1) మరియు
Q నిరూపకాలు (4 – \(\sqrt{5}\), 1)
P వద్ద స్పర్శరేఖ సమీకరణము (4 + \(\sqrt{5}\), 1)
x (4 + \(\sqrt{5}\)) + y . 1 – 4(x + 4 + \(\sqrt{5}\)) – (y + 1) + 12 = 0
⇒ 4x + \(\sqrt{5}\)x + y – 4x – 16 – 4\(\sqrt{5}\) – y – 1 + 12 = 0
⇒ x – 5 – 4\(\sqrt{5}\) = 0
⇒ \(\sqrt{5}\) (x – \(\sqrt{5}\) – 4) = 0
⇒ x – \(\sqrt{5}\) – 4 = 0

x = 4 + \(\sqrt{5}\)
Q వద్ద స్పర్శరేఖ సమీకరణము (4 –\(\sqrt{5}\) , 1)
⇒ x (4 – \(\sqrt{5}\) ) + y. 1 – 4 (x + 4 – \(\sqrt{5}\) ) – (y + 1) + 12 = 0
⇒ 4x – \(\sqrt{5}\)x + y – 4x – 16 + 4\(\sqrt{5}\) – y – 1 + 12 = 0
⇒ – \(\sqrt{5}\)x + 4\(\sqrt{5}\) – 5 = 0
⇒ –\(\sqrt{5}\)(x – 4 + \(\sqrt{5}\)) = 0
⇒ x – 4 + \(\sqrt{5}\) = 0
x = 4 – \(\sqrt{5}\)

ప్రశ్న 7.
x² + y² – 10 = 0 వృత్తానికి x నిరూపకం 1 అయ్యే బిందువుల వద్ద స్పర్శరేఖ సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y² = 10
P నిరూపకాలు (1, y₁)
1+ y₁² = 10 ⇒ y₁² = 9 అనుకొందాం.
y₁ = ±3
P నిరూపకాలు (1, 3) మరియు (1, -3) P(1, 3)
వద్ద స్పర్శరేఖ సమీకరణము
x. 1 + y. 3 = 10
x + 3y – 10 = 0
P(1, 3) వద్ద స్పర్శరేఖ సమీకరణము
x.1 + y(-3) = 10
⇒ x – 3y – 10 = 0

III.

ప్రశ్న 1.
వృత్తం x² + y² = c², సరళరేఖ \(\frac{x}{a}+\frac{y}{b}\) = 1 లు A, B ల వద్ద ఖండించుకుంటే \(\overline{\mathrm{A B}}\) పొడవు కనుక్కొని, ఈ రేఖ వృత్తాన్ని స్పృశించడానికి నియమం కనుక్కోండి.
సాధన:
x² + y² = c²
వృత్త కేంద్రం C = (0, 0), వ్యాసార్ధం (r) = c
d = వృత్త కేంద్రం నుండి జ్యా \(\frac{x}{a}+\frac{y}{b}\) = 1 రేఖ మీదకు లంబదూరం.
= \(\frac{|0-1|}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}=\frac{a b}{\sqrt{a^2+b^2}}\)
ఇక జ్యా పొడవు = 2\(\sqrt{r^2-d^2}\)
= 2\(\sqrt{c^2-\left(\frac{a^2 b^2}{a^2+b^2}\right)}\)
జ్యా వృత్తాన్ని స్పృశిస్తే, జ్యా పొడవు సున్న కావలయును.
⇒ c² = \(\frac{a^2 b^2}{a^2+b^2} \Rightarrow \frac{1}{c^2}=\frac{a^2+b^2}{a^2 b^2}\)
ఇదియే కావలసిన నియమం \(\frac{1}{c^2}=\frac{1}{a^2}+\frac{1}{b^2}\)

ప్రశ్న 2.
x² + y² = a² వృత్తాన్ని, y = mx + c రేఖ A, B ల వద్ద ఖండించుకుంటూ AB = 2λ అయితే c = (1 + m²) (a² – λ²) అని చూపండి.
సాధన:
వృత్త కేంద్రం C (0, 0), వ్యాసార్ధం (r) = a
d = వృత్త కేంద్రం C = (0, 0) నుండి జ్యా y = mx + c

ప్రశ్న 3.
(2, 3) కేంద్రంగా ఉంటూ 3x + 4y + 4 = 0 రేఖపై చేసే జ్యా పొడవు 2 అయ్యే వృత్త సమీకరణాన్ని (Mar. ’11) కనుక్కోండి.
సాధన:
కేంద్రం ( 2, 3) నుండి రేఖ మీదకు దూరం
d = \(\left|\frac{3(-2)+4(3)+4}{\sqrt{9+16}}\right|=\frac{10}{5}\) = 2
జ్యా AB పొడవు = 2 యూనిట్లు

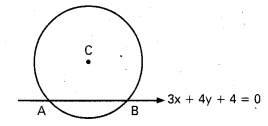
వృత్త వ్యాసార్ధం (r) అనుకొనిన
⇒ 2 = 2\(\sqrt{r^2-d^2}\)
⇒ r² – d² = 1
⇒ r² – 4 = 1 ⇒ r² = 5
వృత్త సమీకరణము
(x + 2)² + (y – 3)² = 5
x² + y² + 4x – 6y + 4 + 9 – 5 = 0
x² + y²+ 4x – 6y + 8 = 0

ప్రశ్న 4.
(3, 2) బిందువు వద్ద x² + y² – x – 3y – 4 = 0 వృత్తానికి స్పర్శరేఖ, అభిలంబ రేఖ సమీకరణాలను కనుక్కోండి.
సాధన:
x² + y² – x − 3y – 4 = 0 వృత్తానికి (3, 2) బిందువు
వద్ద స్పర్శరేఖా సమీకరణం
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(2) + (-\(\frac{1}{2}\)) (x + 3) – \(\frac{3}{2}\) (y + 2) + (-4) = 0
⇒ 6x + 4y – x – 3 – 3y – 6 – 8 = 0
⇒ 5x + y – 17 = 0
అభిలంబరేఖ స్పర్శరేఖకు లంబంగా ఉంటుంది. కనుక P(3, 2) వద్ద అభిలంబ రేఖ x – 5y + k = 0 అనుకుందాం.
ఇది P(3, 2) గుండా పోతుంది కనుక
3 – 10 + k = 0 ⇒ k = 7
∴ P(3, 2) వద్ద అభిలంబ రేఖా సమీకరణం
x – 5y + 7 = 0

ప్రశ్న 5.
(1, 1) బిందువు వద్ద 2x²+ 2y² – 2x – 5y + 3 = 0 వృత్తానికి స్పర్శరేఖ, అభిలంబ రేఖలను కనుక్కోండి.
సాధన:
వృత్త సమీకరణము 2x² + 2y² – 2x 5y + 3 = 0.
⇒ x² + y² – y² – x – \(\frac{5}{2}\) y + \(\frac{3}{2}\) = 0
(1, 1) బిందువు వద్ద x² + y² – x – \(\frac{5}{2}\) y + \(\frac{3}{2}\) = 0
వృత్తానికి స్పర్శరేఖా సమీకరణం
x(1) + y(1) – \(\frac{1}{2}\) (x + 1) – \(\frac{5}{4}\) (y + 1) + \(\frac{3}{2}\) = 0
⇒ 4x + 4y – 2(x + 1) – 5(y + 1) + 6 = 0
⇒ 4x + 4y – 2x – 2 – 5y – 5 + 6 = 0
⇒ 2x – y – 1 = 0
అభిలంబరేఖ స్పర్శబిందువు P(1, 1) వద్ద స్పర్శరేఖకు లంబంగా ఉంటుంది. కనుక అభిలంబరేఖా సమీకరణం x + 2y + k = 0 అనుకుందాం. ఇది P(1, 1) గుండా పోతుందికనుక
1 + 2 + k = 0 ⇒ k = −3
∴ అభిలంబరేఖా సమీకరణం x + 2y – 3 = 0

ప్రశ్న 6.
x² + y² = 13 వృత్తానికి (3, 2) వద్ద గీసిన స్పర్శరేఖ, x² + y² + 2x – 10y – 26 = 0 వృత్తాన్ని స్పృశిస్తుందని చూపి, స్పర్శబిందువును కనుక్కోండి.
సాధన:
x² + y² = 13 వృత్తానికి (3, -2) వద్ద స్వరరేఖాసమీకరణం
x(3) + y (-2) = 13 ⇒ 3x – 2y – 13 = 0 ………………. (1)
వృత్త సమీకరణము x² + y² + 2x – 10y – 26 = 0
కేంద్రం C = (-1,5)
వ్యాసార్ధం (r) = \(\sqrt{1+25+26}=\sqrt{52}=2 \sqrt{13}\)
కేంద్రం C (-1, 5) నుండి 3x – 2y – 13 = 0 రేఖ మీదకు లంబదూరం

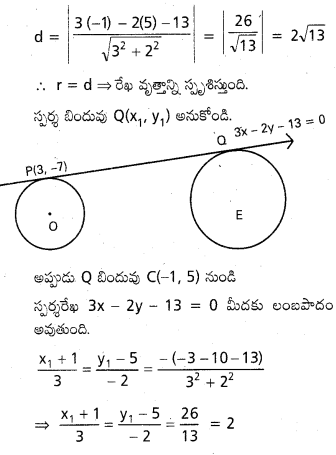
∴ x₁ + 1 = 6 ⇒ x₁ = 5;
∴ y₁ – 5 = -4 ⇒ y₁ = 1
∴ స్పర్శబిందువు = (5, 1)

ప్రశ్న 7.
x² + y² – 4x – 8y + 7 = 0 వృత్తానికి (-1, 2) వద్ద గీసిన స్పర్శరేఖ x² + y² + 4x + 6y = 0 వృత్తాన్ని స్పృశిస్తుందని చూపి, స్పర్శ బిందువును కనుక్కోండి.
సాధన:
x² + y² – 4x – 8y + 7 = 0 వృత్తానికి (-1, 2) వద్ద స్పర్శరేఖ S₁ = 0
అంటే x(-1) + y(2) – 2(x – 1) – 4(y + 2) + 7 = 0
⇒ -3x – 2y + 1 = 0
⇒ 3x + 2y – 1 = 0
ఈ రేఖ x² + y² + 4x + 6y = 0 వృత్తానికి స్పర్శరేఖ అయిన r = d కావలయును.
ఇచ్చట వృత్త వ్యాసార్ధం (r) = \(\sqrt{4+9}=\sqrt{13}\)
d = వృత్త కేంద్రం C (-2, 3) నుండి రేఖ
3x + 2y – 1 = 0 మీదకు లంబదూరం
⇒ d = \(\frac{|3(-2)+2(-3)-1|}{\sqrt{13}}=\sqrt{13}\)
∴ r = d
⇒ రేఖ వృత్తానికి స్పర్శరేఖ అవుతుంది.
స్పర్శబిందువు P(x₁, y₁) అనుకుంటే, ఇది C (-2, -3) నుండి రేఖ మీదకు లంబపాదం అవుతుంది.
\(\frac{x_1+2}{3}=\frac{y_1+3}{2}=-\left(\frac{-6-6-1}{13}\right)\) = 1
⇒ x₁ + 2 = 3 ⇒ x₁ = 1
y₁ + 3 = 2 ⇒ y₁ = -1
∴ స్పర్శబిందువు = (1, −1)

ప్రశ్న 8.
x² + y² – 4x + 6y – 12 = 0 వృత్తానికి x + y − 8 = 0 రేఖకు సమాంతరంగా ఉండే స్పర్శరేఖ సమీకరణం(లు) కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y² – 4x + 6y – 12 = 0
కేంద్రం C (2, -3)
వ్యాసార్ధం (r) = \(\sqrt{4+9+12}=\sqrt{25}\) = 5
x + y – 8 = 0 రేఖకు సమాంతరంగా ఉండే రేఖా సమీకరణం x + y + k = 0 అనుకుందాం.
ఈ రేఖ x² + y² – 4x + 6y – 12 = 0 వృత్తాన్ని
r = d
⇒ 5 = కేంద్రం C (2, 3) నుండి x + y + k = 0 రేఖ మీదకు లంబదూరం
⇒ 5 = \(\frac{|2-3+k|}{\sqrt{1+1}}\)
⇒ 5\(\sqrt{2}\) = |k – 1|
∴ k – 1= = ±5\(\sqrt{2}\) ⇒ k = 1 ± 5\(\sqrt{2}\)
∴ కావలసిన స్పర్శరేఖా సమీకరణాలు
x + y + (1 ± 5 \(\sqrt{2}\)) = 0

ప్రశ్న 9.
x² + y² + 2 x – 2y – 3 = 0 వృత్తానికి 3x y + 4 = 0 రేఖకు లంబంగా ఉండే స్పర్శరేఖా సమీకరణాలను
సాధన:
3x – y + 4 = 0 కు లంబంగా ఉండే రేఖా సమీకరణం x + 3y + k = 0
ఇది వృత్తానికి స్పర్శరేఖ అయిన
r = d
(అంటే) వ్యాసార్ధం = కేంద్రం (−1, 1) నుండి
x + 3y + k = 0 కు లంబదూరం
⇒ \(\sqrt{1+1+3}=\left|\frac{-1+3(1)+k}{\sqrt{10}}\right|\)
⇒ \(\sqrt{50}\) = |k + 2 |
⇒ k + 2 = 5\(\sqrt{2}\)
k = -2 + 5\(\sqrt{2}\)
∴ స్పర్శరేఖా సమీకరణాలు x + 3y – 2 ± 5\(\sqrt{2}\) = 0

ప్రశ్న 10.
x² + y² – 4x – 6y + 3 = 0 వృత్తానికి గీసిన
స్పర్శరేఖ x
అక్షంతో 45° కోణం చేస్తే వాటి
సమీకరణాలను కనుక్కోండి.
సాధన. స్పర్శరేఖ వాలు = tan 45° = 1
కనుక రేఖా సమీకరణం y = x + k
(అంటే) x − y + k = 0 అనుకుందాం
ఇది వృత్తానికి స్పర్శరేఖ అయిన
వ్యాసార్ధం (r) = కేంద్రం C (2, 3) నుండి x – y + k = 0 కు గల లంబదూరం
⇒ \(\sqrt{4+9-3}=\left|\frac{2-3+k}{\sqrt{2}}\right|\)
⇒ \(\sqrt{20}\) = |k – 1|
⇒ k – 1 = ± 2\(\sqrt{5}\) ⇒ k = 1 ± 2\(\sqrt{5}\)
∴ సరళరేఖా సమీకరణాలు x – y + (1 ± 2\(\sqrt{5}\)) = 0

ప్రశ్న 11.
(-1, 0) గుండా పోతూ x + y – 7 = 0 రేఖను (3, 4) వద్ద స్పృశించే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణం
S ≡ x² + y²+2gx + 2fy + c = 0 …………….. (i)
అనుకుందాం
ఇది (-1, 0) గుండా పోతుంది కనుక
1 + 0 – 2g(-1) + 2f(0) + c = 0
⇒ – 2g + c = – 1 …………….. (1)
S = 0 వృత్తం x + y – 7 = 0 రేఖను (3, 4) వద్ద స్పృశిస్తుంది. కనుక (3, 4) వృత్తంపై ఉంటుంది.
⇒ 9 + 16 + 2g(3) + 2f(4) + c = 0
⇒ 6g + 8f + c = 25 …………… (2)
(1) నుండి c = – 1 + 2g
(2) నుండి 6g + 8f + (-1 + 2g) = -25
⇒ 8g + 8f = -24
⇒ g + f = -3
⇒ f = -3 – g
x + y – 7 = 0 రేఖ వృత్తాన్ని స్పృశిస్తుంది కనుక
r = d
⇒ \(\sqrt{g^2+f^2-c}=\left|\frac{(-g)+(-f)-7}{\sqrt{1+1}}\right|\)
⇒ 2(g² + f² – c) = g + f+7)²
⇒ 2[g² + (-3 – g)² – (-1 2g)] = [g – 3 – g + 7]²
⇒ 2 [g² + g² + 9 + 6g + 1 – 2g] = 16
⇒ 2g² + 4g + 10 = 8
⇒g² + 2g + 1 = 0
(g + 1)² = 0 g = − 1
∴ f = – 3 – g = -3(-1) = -2
c = 1 + 2g
⇒ c = (-1) + 2(-1) = -3
∴వృత్త సమీకరణం
x² + y² + 2(-1) x + 2(-2) y + (-3) = 0
⇒ x² + y² – 2x – 4y – 3 = 0

ప్రశ్న 12.
(1, -1) గుండా పోతూ, 4x + 3y + 5 = 0, 3x – 4y – 10 = 0 రేఖలను స్పృశించే వృత్త సమీకరణం కనుక్కోండి.
సాధన:
వృత్త సమీకరణం
x² + y² + 2gx + 2fy + c = 0 ……………. (1)
అనుకుందాం.
ఇది (1, -1) గుండా పోతుంది కనుక
1 + 1 + 2g(1) + 2f(-1) + c = 0
⇒ 2g – 2f + c = -2
∴ c = -2 + 2f – 2g
వృత్త లంబరేఖలు
4x + 3y + 5 = 0, 3x – 4y – 10 = 0 లను స్పృశిస్తుంది. కనుక
కేంద్రం (-g, -f) ⊥ నుండి లంబదూరాల సమూహాలు
\(\left|\frac{-4 g-3 f+5}{5}\right|=\left|\frac{-3 g+4 f+10}{5}\right|\)
-7g + f – 5 = 0 (లేదా) – g – 7f + 15 = 0
f = 7g + 5
ఇప్పుడు \(\left|\frac{-4 g-3 f+5}{5}\right|^2\) = (-g – 1)² + (-f + 1)²
⇒ \(\frac{(-4 g-21 g-15+5)^2}{5}\) = (-g – 1)² + (-7g – 5 + 1)²
⇒(5g + 2)² = g² + 1 + 2g + 16 +49 = g² + 56g
సాధించగా
25g² + 38g + 13 = 0
g = -1, \(\frac{-26}{50}\)
సందర్భం 1 : f = 7g + 5 = f = -2
వృత్తం (1, −1) గుండా పోతుంది.
∴ x² + y² + 2gx + 2fy + c = 0
1 + 1 + 2g – 2f + c = 0
2 – 2 + 4 + c = 0 (లేదా) c = -4
వృత్త సమీకరణము
x² + y² – 2x – 4y – 4 = 0

సందర్భం 2 : -g = \(\frac{-13}{25}\)
f = 7g + 5 = 7(\(\frac{-13}{25}\)) + 5
= \(\frac{-91+125}{25}\) = \(\frac{34}{25}\)
వృత్తం (1, – 1) గుండా పోతుంది.
x² + y² + 2gx + 2fy + c = 0.
x² + y²+ \(\frac{26}{25}\)x + \(\frac{68}{25}\)y + c = 0
1 + 1 – \(\frac{26}{25}\) – \(\frac{68}{25}\) + c = 0
c = -2 + \(\frac{26}{25}\) + \(\frac{68}{25}\) = \(\frac{-50+26+68}{25}\) = \(\frac{44}{25}\)
∴ వృత్త సమీకరణము
x² + y² – \(\frac{26}{25}\)x + \(\frac{68}{25}\)y + \(\frac{44}{25}\) = 0
25 (x² + y²) – 26x + 68y + 44 = 0

ప్రశ్న 13.
x + y + 10 రేఖ x²+ y² – 3x + 7y+ 14 = 0 వృత్తాన్ని స్పృశిస్తుందని చూపి, స్పర్శ బిందువును కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y² – 3x + 7y + 14 = 0
వృత్త కేంద్రము C = \(\left(\frac{3}{2}, \frac{-7}{2}\right)\)
వృత్త వ్యాసార్ధము (r) = \(\sqrt{\frac{9}{4}+\frac{49}{4}-14}\)
= \(\frac{\sqrt{58-56}}{4}=\frac{1}{\sqrt{2}}\)
కేంద్రం C నుండి రేఖ x + y + 1 = 0 కు లంబదూరం
d = \(\frac{\left|\frac{3}{2}-\frac{7}{2}+1\right|}{\sqrt{1+1}}=\frac{1}{\sqrt{2}}\)
∴ r = d = \(\frac{1}{\sqrt{2}}\)
రేఖ వృత్తాన్ని స్పృశిస్తుంది.
రేఖ వృత్తాన్ని P(h, k) వద్ద స్పృశిస్తుంది అనుకొనుము.

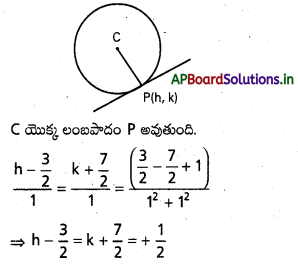
⇒ h = 2, k = -3
∴ స్పర్శ బిందువు (2, -3)