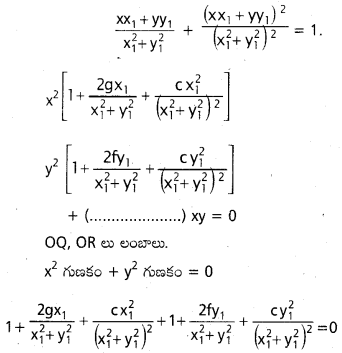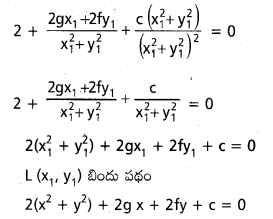AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Ex 1(d)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 1 వృత్తం Exercise 1(d) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Exercise 1(d)

అభ్యాసం – 1 (డి)

I.

ప్రశ్న 1.
S ≡ x² + y² + 2gx + 2fy + c = 0 వృత్తానికి (0, 0) నుంచి గీసిన స్పర్శరేఖలు లంబంగా ఉండటానికి నియమం కనుక్కోండి.
సాధన:
P నుండి వృత్తానికి గీయబడిన స్పర్శరేఖలు వృత్త కోణము θ

1 = \(\frac{\sqrt{g^2+f^2-c}}{\sqrt{0+0+0+0}+c}\)
g² + f² – c = c
g² + f² = 2c
ఇది కావలసిన నియమము

ప్రశ్న 2.
x² + y² – 5x + 4y – 2 = 0 వృత్తం దృష్ట్యా (0, 5) స్పర్శ జ్యా సమీకరణాన్ని కనుక్కోండి.
సాధన:
స్పర్శ జ్యా సమీకరణము S₁ = 0
i.e., xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0 వృత్త సమీకరణము
S = x² + y² – 5x + 4y – 2 = 0
స్పర్శ జ్యా సమీకరణము
x. 0 + y. 5 – \(\frac{5}{2}\) (x + 0) + 2(y + 5) – 2 = 0
2 తో గుణించగా
10y – 5x + 4y + 20 – 4 = 0
-5x + 14y + 16 = 0
లేదా 5x – 14y – 16 = 0

ప్రశ్న 3.
x² + y² = 9 వృత్తం దృష్ట్యా (1, 1) స్పర్శ జ్యా సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y ² = 9
వృత్తం దృష్ట్యా (1, 1) స్పర్శ జ్యా సమీకరణం S₁ = 0
(i.e.,) x(1) + y(1) – 9 = 0
(i.e.,) x + y – 9 = 0

ప్రశ్న 4.
x² + y² = 7 వృత్తం దృష్ట్యా (1, 2) ధ్రువ రేఖను కనుక్కోండి.
సాధన:
x² + y² = 7 వృత్తం దృష్ట్యా (1, 2) ధ్రువరేఖ S₁= 0
(i.e.,) x(1) + y(2) – 7 = 0
⇒ x + 2y – 7 = 0

ప్రశ్న 5.
2x² + 2y² = 11 వృత్తం దృష్ట్యా (3, -1) ధ్రువ రేఖను కనుక్కోండి.
సాధన:
దత్త సమీకరణం 2x² + 2y² = 11
⇒ x² + y² = \(\frac{11}{2}\) వృత్తం దృష్ట్యా (3, −1)
ధృవరేఖ S₁ = 0
x(3) + (-1) y = \(\frac{11}{2}\)
6x – 2y – 11 = 0.

ప్రశ్న 6.
x² + y² – 10x – 10y + 25 = 0 దృష్ట్యా (1, 2) యొక్క ధ్రువరేఖా సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
x² + y²-10x-10y + 25 = 0
దృవరేఖ సమీకరణము S₁ = 0
P(1, 2) యొక్క దృవరేఖ
x.1 + y(-2) – 5(x + 1) – 5(y – 2) + 25 = 0
x – 2y – 5x – 5 – 5y + 10 + 25 = 0
-4x – 7y + 30 = 0
4x + 7y – 30 = 0

ప్రశ్న 7.
c ≠ 0 అయితే x² + y² = r² వృత్తోం దృష్ట్యా ax + by + c = 0, యొక్క ధ్రువాన్ని కనుక్కోండి.
సాధన:
ధ్రువం (x₁, y₁) అనుకుందాం.
ధ్రువరేఖ xx₁ + yy₁ – r² = 0 ……………. (1)
ధ్రువరేఖ ax + by + c = 0 ………………. (2)
(1) మరియు (2) నుండి \(\frac{x_1}{a}=\frac{y_1}{b}=\frac{-r^2}{c}\)
⇒ x₁ = \(\frac{-a r^2}{c}\), y₁ = \(\frac{-b r^2}{c}\)
∴ ధ్రువం \(\left(\frac{-a r^2}{c}, \frac{-b r^2}{c}\right)\), (c ≠ 0)

ప్రశ్న 8.
x²+ y² – 6x – 8y + 5 = 0 వృత్తానికి 3x + 4y – 45 = 0 ధ్రువ రేఖ అయితే దీని ధ్రువాన్ని కనుక్కోండి. [A.P. Mar. ’16]
సాధన:
ధ్రువం p (x₁, y₁) అనుకుందాం.
ధ్రువరేఖ సమీకరణం S₁ = 0
⇒ xx₁ + yy₁ – 3(x + x₁) – 4(y + y₁) + 5 = 0
⇒ x(x₁ – 3) + y(y₁ – 4) – 3x₁ -4y₁ + 5 = 0 ……………. (1)
కాని రేఖ 3x + 4y – 45 = 0 ……………. (2)
(1), (2) ల నుండి
\(\frac{x_1-3}{3}=\frac{y_1-4}{4}=\frac{-3 x_1-4 y_1+5}{-45}\) = k అనుకుందాం
⇒ x₁ = 3k + 3, y₁ = 4k + 4
-3x₁ – 4y₁ + 5 = -45k
⇒ -3(3k + 3) – 4(4k + 4) + 5 = -45k
⇒ 20k – 20 = 0 ⇒ k = 1
⇒ \(\frac{x_1-3}{3}=\frac{y_1-4}{4}\)
∴x₁ = 3(1) + 3 = 6, y₁ = 4(1) + 4 = 8
∴ ధ్రువం = (6, 8).

ప్రశ్న 9.
x²+ y² – 5x + 8y + 6 = 0 వృత్తానికి x – 2y + 22=0 ఒక ధ్రువరేఖ అయితే దీని ధ్రువాన్ని కనుక్కోండి.
సాధన:
ధ్రువం p (x₁, y₁) అనుకుందాం.
ధ్రువరేఖ సమీకరణం S₁ = 0
xx₁ + yy₁ – \(\frac{5}{2}\) (x + x₁) + 4 (y + y₁) + 6 = 0
(లేదా) x(x₁ – \(\frac{5}{2}\)) + y (y₁ + 4) – \(\frac{5}{2}\)
x₁ + 4y₁ + 60 = 0 ………… (i)
x – 2y + 22 = 0 …………..(ii)
(i), (ii) లు ఒకే రేఖలను సూచిస్తున్న
\(\frac{x_1-\frac{5}{2}}{1}=\frac{y_1+4}{-2}=\frac{\frac{-5}{2} x_1+4 y_1+6}{22}\) = k
x₁ – \(\frac{5}{2}\) = k ⇒ x₁ = k + \(\frac{5}{2}\)
– \(\frac{5}{2}\) x₁ + 4y₁ + 6 = 22k
y₁ = -2k – 4,
–\(\frac{5}{2}\) (k + \(\frac{5}{2}\)) + 4 (-2k – 4) + 6 = 22k ;
–\(\frac{5k}{2}\) – \(\frac{25}{4}\) – 8k – 16 + 6 = 22k
–\(\frac{65}{4}\) = 30k + \(\frac{5k}{2}\) = \(\frac{65k}{2}\)
k = –\(\frac{5}{2}\) ; x₁ = –\(\frac{1}{2}\) + \(\frac{5}{2}\) = 2
y₁ = -3
∴ ధ్రువము (2, – 3)

ప్రశ్న 10.
x²+ y² – 2x + 2y + 1 = 0 వృత్తం దృష్ట్యా (-6, 1), (2, 3) లు సంయుగ్మ బిందువులని చూపండి.
సాధన:
S = 0 వృత్తం దృష్ట్యా P(x₁, y₁), Q(x₂, y₂) లు సంయుగ్మాలైన S₁₂ = 0
కనుక ఇచ్చట వృత్త సమీకరణం
x² + y² – 2x + 2y + 1 = 0
బిందువులు P (-6, 1), Q (2, 3)
ఇప్పుడు S₁₂ = x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c
= (-6) (2) + (1) (3) + (-1) (-6 + 2) + 1(1 + 3) + 1
= -12 + 3 + 4 + 4 + 1 = 12 + 12 = 0
∵ S₁₂ = 0
⇒ వృత్తం దృష్ట్యా దత్త బిందువులు సంయుగ్మ బిందువులు.

ప్రశ్న 11.
x² + y² – 3x – 5y + 1 = 0 వృత్తం దృష్ట్యా (4, 2), (3, −5) లు సంయుగ్మ బిందువులని చూపండి.
సాధన:
దత్త బిందువులు సంయుగ్మాలైన S₁₂ = 0 కావలయును.
అంటే S₁₂ = (4) (3) + (2) (-5) – \(\frac{3}{2}\) (4 + 3) – \(\frac{5}{2}\) (2 – 5) + 1
S₁₂ = 12 – 10 – \(\frac{21}{2}\) + \(\frac{15}{2}\) + 1
S₁₂ = 3 – 3 = 0
∴ దత్త బిందువులు వృత్తం దృష్ట్యా సంయుగ్మాలు.

ప్రశ్న 12.
x² + y² – 2x – 4y – 4 = 0 వృత్తం దృష్ట్యా kx + 3y – 1 = 0, 2x + y + 5 = 0 లు సంయుగ్మ రేఖలయితే k విలువ కనుక్కోండి.
సాధన:
దృవము (x₁, y₁) దృవరేఖ సమీకరణము
x² + y² – 2x – 4y – 4 = 0
xx₁ + yy₁ – 1(x + x₁) – 2(y + y₁) – 4 = 0
x(x₁ – 1) + y(y₁ – 2) – x₁ – 2y₁ – 4 = 0 ……………… (i)
2x + y + 5 = 0 (i) తో పోల్చగా

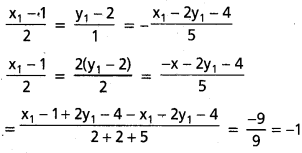
x₁ = -1, y₁ = 1 ద్రువము (−1, 1)
kx + 3y – 1 = 0 దృవరేఖ అయితే (-1, 1) ను తృప్తిపరచవలెను.
k(-1) + 3(1) – 1 = 0
-k + 2 = 0
k = 2

ప్రశ్న 13.
x² + y² – 2x – 2y – 1 = 0 వృత్తం దృష్ట్యా x + y – 5 = 0, 2x + ky – 8 = 0 లు సంయుగ్మ రేఖలయితే k విలువ కనుక్కోండి.
సాధన:
If l₁x + m₁y + n₁ = 0; l₂x + m₂y + n₂ = 0, S = 0 దృష్ట్యా సంయుగ్మ రేఖలయితే
r²(l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
l₁ = 1, m₁ = 1, n₁ = -5
l₂ = 2, m₂ = k, n₂ =-8
g = -1, f = -1, r² = 3
∴ 3(1.2 + k) = (-1 – 1 + 5) (-2 – k + 8)
6k = 18 – 6 = 12
⇒ k = 2

ప్రశ్న 14.
x² + y² = 35 వృత్తం దృష్ట్యా (1, 3), (2, k) ∞ సంయుగ్మాలయితే k విలువ కనుక్కోండి. [T.S. Mar. ’17 T.S. Mar. ’16]
సాధన:
వృత్త సమీకరణం x² + y² = 35 యొక్క దృవరేఖ P(1, 3)
x. 1 + y. 3 = 35
x + 3y = 35
P(1, 3), Q(2, k) లు సంయుగ్మ బిందువులయితే
P యొక్క దృవరేఖ Q గుండా పోతుంది.
2 + 3k = 35
3k = 33
k = 11

ప్రశ్న 15.
x² + y² – 5x + 8y + 6 = 0 వృత్తం దృష్ట్యా (4, 2), (k, -3) లు సంయుగ్మాలయితే k విలువ ఎంత ? [A.P. Mar. ’17]
సాధన:
వృత్త సమీకరణం x² + y² – 5x + 8y + 6 = 0 యొక్క దృవరేఖ (4, 2)
x.4 + y.2 – \(\frac{5}{2}\)(x + 4) + 4 (y + 2) + 6 = 0
8x + 4y – 5x – 20 + 8y + 16 + 12 = 0
3x + 12y + 8 = 0
P(4, 2), Q(k, -3) లు సంయుగ్మాలు.
P యొక్క దృవరేఖ Q గుండా పోతుంది.
∴ 3k – 36 + 8 = 0
3k = 28 ⇒ k = \(\frac{28}{3}\)

II.

ప్రశ్న 1.
(3, 2) బిందువు నుంచి x²+y²-6x+4y-2=0 వృత్తానికి గీసిన స్పర్య రేఖల మధ్య కోణం కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
S ≡ x² + y² – 6x + 4y – 2 = 0
r = \(\sqrt{9+4+2}\) = \(\sqrt{15}\)
S₁₁ = 9 + 4 – 18 + 8 – 2 = 1

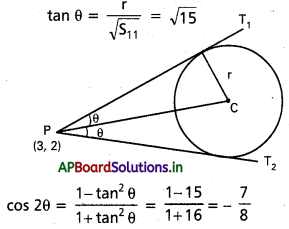
P వద్ద స్పర్శరేఖల మధ్య కోణము cos^-1\(\left(\frac{7}{8}\right)\)

ప్రశ్న 2.
(1, 3) బిందువు నుంచి x² + y² – 2x + 4y – 11 = 0 వృత్తానికి గీసిన స్పర్శ రేఖల మధ్య కోణం కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
S ≡ x² + y² – 2x + 4y – 11 = 0
r = \(\sqrt{1+4+11}\) = 4
S₁₁ = 1 + 9 – 2 + 12 – 11 = 9

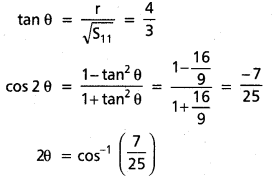
స్పర్శరేఖల మధ్య కోణము cos^-1\(\left(\frac{7}{25}\right)\)

ప్రశ్న 3.
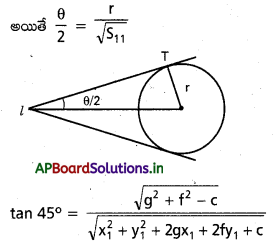
(0, 0) బిందువు నుంచి x² + y² – 14x + 2y + 25 = 0 వృత్తానికి గీసిన స్పర్శరేఖల మధ్య కోణం కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y² – 14x + 2y + 25 = 0
కేంద్రం C = (7, -1),
వ్యాసార్థం (r) = \(\sqrt{49+1-25}\) = \(\sqrt{25}\) = 5
S₁₁ = 0 + 0 – 0 + 0 + 25 = 25
స్పర్శరేఖల మధ్య కోణము ‘θ’ అయిన
tan (θ/2) = \(\frac{r}{\sqrt{s_{11}}}=\frac{5}{\sqrt{25}}\) = 1
∴ \(\frac{\theta}{2}=\frac{\pi}{4}\) ⇒ θ = \(\frac{\pi}{2}\)
∴ స్పర్శరేఖల మధ్య కోణము θ = 90°

ప్రశ్న 4.
ఏదైనా బిందువు P నుంచి x² + y² = a² వృత్తానికి గీసిన స్పర్శరేఖల మధ్య కోణం a అయ్యేటట్లు ఉండే P బిందు పథం కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y² = a²
r = వ్యాసార్థము = a
P (x₁, y₁) బిందు పథము మీది బిందువు
S₁₁ = x² + y² – a²

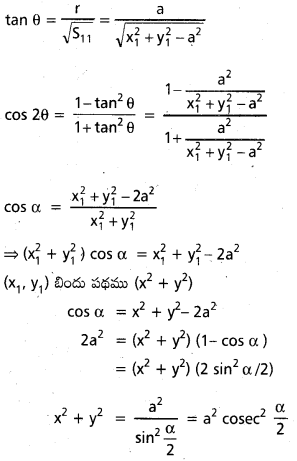
ప్రశ్న 5.
ఏదైనా బిందువు P నుంచి x² + y² = a² వృత్తానికి గీసిన స్పర్శరేఖలు లంబంగా ఉండేటటువంటి P బిందు పథాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y² = a²
r = a
P(x₁, y₁) బిందు పథం మీది బిందువు
S₁₁ = x₁² + y₁² – a²
tan θ = \(\frac{r}{\sqrt{s_{11}}}=\frac{a}{\sqrt{x_1^2+y_1^2-a^2}}\)
ఇచ్చిన 2θ = \(\frac{\pi}{2}\) ⇒ θ = \(\frac{\pi}{4}\)
⇒ tan θ = tan \(\frac{\pi}{4}\) = 1
∴ \(\frac{d}{\sqrt{x_1^2+y_1^2-a^2}}\) = 1
వర్గీకరించి, అడ్డ గుణకారం చేయగా
a² = x² + y² – a²
x₁² + y₁² = 2a²
P (x, y ) బిందు పథము x² + y² = 2a²

ప్రశ్న 6.
x² + y² – 4x – 4y – 4= 0 వృత్తానికి (1,3) ధ్రువ రేఖ వాలు, వృత్తకేంద్రం నుంచి, ఈ ధ్రువ రేఖకు గల లంబ దూరాన్ని కనుక్కోండి.
సాధన:
x² + y² – 4x – 4y – 4 = 0
వృత్తానికి (1,3) ధ్రువరేఖ S₁ =0
(i.e.,) x(1) + y(3) – 2(x + 1) – 2(y + 3) – 4 = 0
⇒ -x + y – 12 = 0
⇒ x + y + 12 = 0
∴ ధ్రువరేఖ వాలు = \(\frac{-(1)}{1}\) = 1
వృత్త కేంద్రం C =(2, 2) నుండి ధ్రువరేఖ x – y + 12 = 0
కు లంబదూరం
= \(\left|\frac{2-2+12}{\sqrt{1+1}}\right|=\frac{12}{\sqrt{2}}\)
= 6 \(\sqrt{2}\)యూనిట్లు.

ప్రశ్న 7.
x² + y² – 2x + 2y + 1 = 0 వృత్తం దృష్ట్యా (1, 1) ధ్రువ రేఖ సమీకరణం ax + by + c = 0 అయి a, b, c ల గరిష్ఠ సామాన్య భాజకం 1 అయితే a² + b² + c విలువను కనుక్కోండి.
సాధన:
x² + y² – 2x + y + 1 = 0 వృత్తం దృష్ట్యా (1,1)
ధ్రువరేఖ S₁ = 0.
(i.e.,) x(1) + y(1) – (x + 1) + (y + 1) + 1 = 0
⇒ 2y + 1 = 0 ………………. (1)
కాని ధ్రువరేఖా సమీకరణం ax + by + c = 0 ……………… (2)
(1), (2) లు ఒకే రేఖను సూచిస్తున్నాయి కనుక
\(\frac{a}{0}=\frac{b}{2}=\frac{c}{1}\)
⇒a = : 0, b = 2, c = 1
(a, b, c ల గరిష్ఠ సామాన్య భాజకం 1)
∴ a² + b² + c² = 0 + 4 + 1 = 5

III.

ప్రశ్న 1.
x + 4y – 14=0 రేఖ x² + y² – 2x + 3y – 5=0 వృత్తాన్ని ఖండించే బిందువుల వద్ద గీసిన స్పర్శ రేఖల ఖండన బిందువును కనుక్కోండి.
సాధన:
దత్త వృత్త సమీకరణము
x² + y² – 2x + 3y – 5 = 0
P(x, y) యొక్క ధృవరేఖ

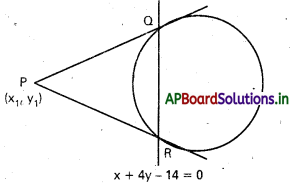
xx₁ + yy₁ – 1(x + x₁) + \(\frac{3}{2}\) (y + y₁) – 5 = 0
2xx₁ + 2yy₁ – 2x – 2x₁ + 3y+ 3y₁ – 10 = 0
2(x₁ – 1)x + (2y₁ + 3) y -(2x₁ – 3y₁ + 10) = 0 ……………… (1)
QR సమీకరణము 5x + 4y – 14 = 0 …………….. (2)
(1) మరియు (2) పోల్చగా
\(\frac{2\left(x_1-1\right)}{1}=\frac{2 y_1+3}{4}=\frac{2 x_1-3 y_1+10}{14}\)
2(x₁ – 1) = \(\frac{2 y_1+3}{4}\)
8x₁ – 8 = 2y₁ + 3
8x₁ – 2y₁ = 11 ………………. (1)
2(x₁ – 1) = \(\frac{2 x_1-3 y_1+10}{14}\)
28x₁ – 28 = 2x₁ – 3y₁ + 10
26x₁ + 3y₁ = 38 ……………….. (2)

ప్రశ్న 2.
x² + y² = b² వృత్తం దృష్ట్యా x² + y² = a² వృత్తంపై ఉండే బిందువుల ధృవరేఖలు x² + y² = c² వృత్తాన్ని స్పృశిస్తే a,b,c లు గుణశ్రేఢిలో ఉంటాయని చూపండి.
సాధన:

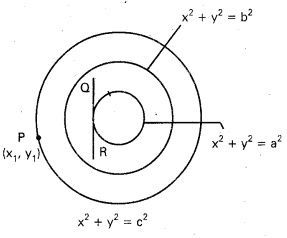
P(x₁, y₁) బిందువు మీది బిందువు x² + y² = a²
∴ x₁² + y₁² = a² ……………. (1)
x²+ y²= b² దృష్ట్యా P యొక్క ధ్రువరేఖ
xx₁ + yy₁ = b²
ఈ రేఖ x² + y² = c² వృత్తానికి స్పర్శరేఖ
\(\frac{\left|0+0-\mathrm{b}^2\right|}{\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2}}\) = c ⇒ \(\frac{b^2}{a}\) = c
అడ్డ గుణకారం చేయగా b2 = ac
∴ a, b, c లు G. P. లో ఉన్నాయి.

ప్రశ్న 3.
P (3, 5) నుంచి x² + y² = 16 వృత్తానికి రెండు స్పర్శరేఖలు గీశాం. ఈ స్పర్శరేఖలు, దత్త వృత్తం దృష్ట్యా P యొక్క స్పర్శ జ్యాతో ఏర్పడే త్రిభుజ వైశాల్యాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x² + y² = 16

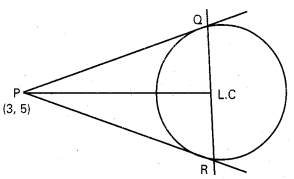
P (3, 5) యొక్క ధృవరేఖ 3x + 5y = 16
PL = P యొక్క లంబకోణము
= \(\frac{|9+25-16|}{\sqrt{9+25}}=\frac{18}{\sqrt{34}}\)
కేంద్రం = C (0, 0)
P = c మీదకు లంబదూరము

ప్రశ్న 4.
4x²+ y² – 4x – 4y – 8 = 0, x² + y² – 2x + 6y – 2 = 0 వృత్తాలకు ఒక బిందువు దృష్ట్యా ఏర్పడే ధ్రువ రేఖలు లంబంగా ఉంటే, ఆ చర బిందువు యొక్క బిందు వధ సమీకరణాన్ని కనుక్కోండి.
సాధన:
P(x, y) బిందు పథము మీది బిందువు
వృత్తాల సమీకరణాలు
x² + y² – 4x – 4y – 8 = 0 ……………… (1)
x² + y² – 2x + 6y – 2 = 0 ………………. (2)
(1) దృష్ట్యా P యొక్క ధృవరేఖ
xx₁ + yy₁ – 2(x + x₁) – 2 (y + y₁) – 8 = 0
x(x₁ – 2) + y (y₁ – 2) – (2x₁ + 2y₁ + 8) = 0(3)
(2) వ వృత్తం దృష్ట్యా P యొక్క ధృవరేఖ సమీకరణాలు
xx₁ + yy₁ – 1(x + x₁) – 3 (y + y₁) – 2 = 0
xx₁ + yy₁ – x – x₁ + 3y + 3y₁ – 2 = 0
x(x₁ – 1) + y (y₁ + 3) – (x₁ + 3y₁ + 2) = 0
(3), (4) లు లంబంగా ఉన్నాయి.
⇒ a₁a₂ + b₁b₂ = 0
(x₁ – 2) (x₁ – 1) + (y₁ – 2) (y₁ + 3) = 0
x₁² – 3x₁ +2 + y₁² + y₁ – 6 = 0
x₁² + y₁² – 3x₁ + y₁ – 4 = 0 x² + y² – 3×1 + Y1
p(x₁, y₁) బిందు పథము x² + y² – 3x + y – 4 = 0

ప్రశ్న 5.
S ≡ x² + y² + 2gx + 2fy + c = 0 యొక్క ఏదైనా జ్యా, మూల బిందువు వద్ద 90° కోణం ఏర్పరిస్తే మూల బిందువు నుంచి ఆ జ్యాకు గీసిన లంబ పాదాల బిందుపథాన్ని కనుక్కోండి.
సాధన:

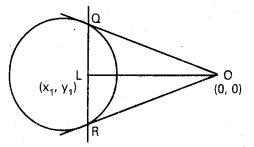
QL మీదకు మూల బిందువు నుండి గీయబడిన లంబ పాదము L (x₁, y₁)
QL వాలు = \(\frac{y_1}{x_1}\)
QR వాలు = –\(\frac{x_1}{y_1}\)
QR సమీకరణము y – y₁ = –\(\frac{x_1}{y_1}\) (x – x₁)
yy₁ – y₁²1 = – xx₁ + x₁².
xx₁ + yy₁ = x₁² + y₁²
(లేదా) \(\frac{x x_1+y y_1}{x_1^2+y_1^2}\) = 1 …………. (1)
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0 …………….. (2)
(2) సహాయంతో (1) ని సమఘాతపరచగా OQ, OR ల ఉమ్మడి సమీకరణము
x² + y² + (2gx + 2fy)