AP Inter 2nd Year Maths 2B Solutions Chapter 2 వృత్త సరణులు Ex 2(a)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 2 వృత్త సరణులు Exercise 2(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 2 వృత్త సరణులు Exercise 2(a)

అభ్యాసం – 2(ఎ)

I.

ప్రశ్న 1.
క్రింది సమీకరణాలు సూచించే ప్రతి జత వృత్తాలు లంబ వృత్తాలు అయితే k విలువ కనుక్కోండి.
i) x² + y² + 2by – k = 0, x² + y² + 2ax + 8 = 0
సాధన:
g₁ = 0;
g₂ = a ;
f₁ = b;
f₂ = 0
c₁ = -k
c₂ = 8
దత్త వృత్తాలు లంబంగా ఖండించుకొంటున్నాయి.
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(0) (a) + 2(b) (0) = -k + 8
0 = – k + 8
k = 8

ii) x²+ y² – 6x – 8y + 12 = 0; x² + y² – 4x + 6y + k = 0
సాధన:
g₁ = -3
g₂ = -2
f₁ = -4
f₂ = 3
c₁ = 12
c₂ = k
దత్త వృత్తాలు లంబంగా ఖండించుకొంటున్నాయి
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(-3) (-2) + 2(3) (-4) = 12 + k
-12 – 24 = 12 + k
k = -24

iii) x² + y² – 5x – 14y – 34 = 0; x²+ y² + 2x + 4y + k = 0
సాధన:
g₁ = \(\frac{-5}{2}\)
g₂ = 1
f₁ = -7
f₂ = 2
c₁ = -34
c₂ = k
దత్త వృత్తాలు లంబంగా ఖండించుకొంటున్నాయి
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2 (\(\frac{-5}{2}\)) (1) + 2(-7) (2) = – 34 + k
-5 – 28 = -34 + k
-33 = – 34 + k
k = 34 – 33 ⇒ k = 1

iv) x² + y² + 4x + 8 = 0; x² + y² – 16y + k = 0 [T.S. Mar. ’16 A.P. Mar. ’16]
సాధన:
g₁ = 2
g₂ = 0
f₁ = 0
f₂ = -8
c₁ = 8
c₂ = k
దత్త వృత్తాలు లంబంగా ఖండించుకొంటున్నాయి
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(2) (0) + 2(0) (-8) = 8+ k
0 + 0 = 8+ k
⇒ k = -8

ప్రశ్న 2.
క్రింది సమీకరణాలు సూచించే వృత్తాల మధ్య కోణాన్ని కనుగొనుము.
i) x² + y² – 12x – 6y + 41 = 0; x² + y²+ 4x + 6y – 59 = 0
సాధన:
C₁ = (6, 3)
C₂ = (-2, -3)
r₁ = (36 + 9 – 41)^1/2
r₂ = (4 + 9 + 59)^1/2
r₁ = 2
r₂ = (72)^1/2 = 6\(\sqrt{2}\)

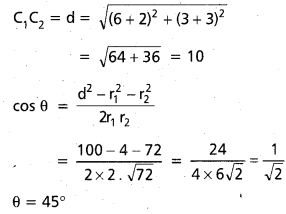
ii) x² + y² + 6x – 10y – 135 = 0; x² + y² – 4x + 14y – 116 = 0
సాధన;
C₁ = (-3, 5)
C₂ = (2, -7)
r₁ = \(\sqrt{9+25+135}\)
r₂ = \(\sqrt{4+49+116}\)
r₁ = 13
r₂ = 13

ప్రశ్న 3.
x² + y² = a², x² + y² = ax + ay సమీకరణాలు సూచించే వృత్తాల మధ్యకోణం \(\frac{3\pi}{4}\) అని చూపండి.
సాధన:
వృత్తాల సమీకరణాలు
S ≡ x² + y² – a² = 0
S’ ≡ x²+ y² – ax – ay = 0

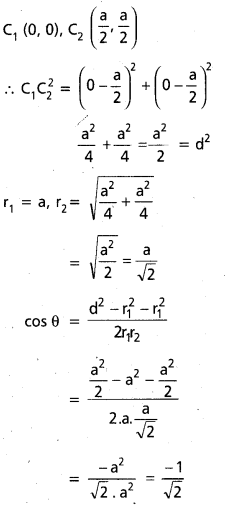
= cos \(\frac{3\pi}{4}\)
θ = \(\frac{3\pi}{4}\)

ప్రశ్న 4.
క్రింది సమీకరణాలు సూచించే వృత్తాలు ఒకదానికొకటి లంబంగా ఖండించుకుంటాయని చూపండి.
i) x² + y² – 2x – 2y – 7 = 0; 3x² + 3y² – 8x + 29y = 0
సాధన:
C₁ = (1, 1)
g = -1, f = -1, c = 7
g’ = \(\frac{-4}{3}\), f’ = \(\frac{29}{6}\) ; c’ = 0
దత్త వృత్తాలు లంబంగా ఖండించుకొనే నియమము
2gg’ + 2ff’ = c + c’
2(-1) (\(\frac{-4}{3}\)) + 2(-1) \(\frac{29}{6}\) = -7 + 0
L.H.S. = \(\frac{8}{3}\) – \(\frac{29}{3}\)
= \(\frac{-21}{3}\) = -7
-7 = -7
∴ రెండు వృత్తాలు లంబంగా ఖండించుకుంటాయి.

ii) x² + y² +4x – 2y – 11 = 0; x² + y² – 4x – 8y + 11 = 0
సాధన:
g₁ = 2
g₂ = -2
f₁ = -1
f₂ = -4
c₁ = -11
c₂ = 11
రెండు వృత్తాలు లంబంగా ఖండించుకొంటే
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(2)(-2) + 2(-1) (-4) = -11 + 11
-8 + 8 = 0
∴ రెండు వృత్తాలు లంబంగా ఖండించుకుంటాయి.

iii) x² + y² – 2x + 4y + 4 = 0; x² + y² + 3x + 4y + 1 = 0
సాధన:
g = -1, f = 2, c = 4
g’ = \(\frac{3}{2}\), f’ = 2, c’ = 1
దత్త వృత్తాలు లంబంగా ఖండించుకునే నియమం
2gg’ + 2ff’ + c’
2(-1) . \(\frac{3}{2}\) + 2×2×2 = 4 + 1
-3 + 8 = 5
5 = 5
∴ దత్త వృత్తాలు లంబంగా ఖండించుకుంటాయి.

iv) x² + y² – 2lx + g = 0; x²+ y² + 2my – g = 0
సాధన:
g₁ = -1; f₁ = 0, c₁ = g, g₂ = 0, f₂ = m, c₂ = g
దత్త వృత్తాలు లంబంగా ఖండించుకొనే నియమము
2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(-l) (0) + 2(0) (m) = g – g
0 = 0
∴ రెండు వృత్తాలు లంబంగా ఖండించుకుంటాయి.

II.

ప్రశ్న 1.
మూలబిందువు గుండా పోతూ కింది సమీకరణాలు సూచించే వృత్తాలను లంబంగా ఖండించే వృత్తాల సమీకరణాలను కనుక్కోండి.
i) x² + y² – 4x + 6y + 10 = 0, x² + y² + 12y + 6 = 0
సాధన:
వృత్త సమీకరణాలు
x² + y² – 4x + 6y + 10 = 0,
x² + y² + 12y + 6 = 0
మూల బిందువు గుండా పోయే వృత్త సమీకరణం
x² + y² + 2gx + 2fy = 0 ……………… (1)
ఇది దత్త వృత్తాలను లంబంగా ఖండిస్తే
2(g) (−2) + 2f(3) = 0 + 10
⇒ – 2g + 3f = 5 ……………… (2)
2(g) (0) + 2f(6) = 0 + 6
⇒ f = \(\frac{1}{2}\)
(2) లో వ్రాయగా
-2(g) + \(\frac{3}{2}\) = 5 ⇒ g = \(\frac{-7}{4}\)
∴ కావలసిన వృత్త సమీకరణం
x² + y² + 2(\(\frac{-7}{4}\))x + 2(\(\frac{1}{2}\)) y = 0
⇒ 2(x² + y²) – 7x + 2y = 0

ii) x² + y² – 4x – 6y – 3 = 0, x² + y² – 8y + 12 = 0
సాధన:
వృత్త సమీకరణాలు
x²+ y² – 4x – 6y – 3 = 0
x²+ y² – 8y + 12 = 0
మూల బిందువు గుండా పోయే వృత్త సమీకరణం
x² + y² + 2gx + 2fy = 0 ……………… (1)
ఇది దత్త వృత్తాలను లంబంగా ఖండిస్తుంది కనుక
2(g) (-2)+2(f)(-3) = 0 + (-3).
⇒ – 4g – 6f = -3
⇒ 4g + 6f = 3 ………………… (2)
ఇట్లే 2(g) (0) + 2f(−4) = 0 + 12
⇒ f = –\(\frac{3}{2}\)
(2) లో వ్రాయగా
4g + 6(\(\frac{-3}{2}\)) = 3
⇒ 4g = 12 ⇒ g = 3
∴వృత్త సమీకరణం x² + y² + 6x – 3y = 0

ప్రశ్న 2.
x² + y² – 6x + 3y + 5 = 0, x² + y² – x – 7y = 0 సమీకరణాలు సూచించే వృత్తాలను లంబంగా ఖండిస్తూ, బిందువు (0,-3) గుండా పోయే వ్యక్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణం
x² + y² + 2gx + 2fy + c = 0 ……………… (i)
అనుకుందాం.
ఇది (0, -3) గుండా పోతుంది కనుక
0 + 9 + 0 – 6f + c = 0
⇒ 6f + c = – 9 ……………… (1)
వృత్తం (i) దత్త వృత్తాలను లంబంగా ఖండిస్తుంది కనుక
2(g) (-3) + 2f(\(\frac{3}{2}\)) = c + 5
⇒ -6g + 3f – c = 5 ………………. (2)
ఇట్లే 2g(\(\frac{-1}{2}\)) + 2f(\(\frac{-7}{2}\)) = c + 0
⇒ -g – 7f = c
⇒ g + 7f + c = 0 ……………….. (3)

(1) నుండి – 6 (\(\frac{2}{3}\)) + c = -9
⇒ c = -9 + 4 = -5
(3) నుండి g + 7 (\(\frac{2}{3}\)) + (-5) = 0
g = \(\frac{-14}{3}\) + 5 = \(\frac{1}{3}\)
∴ కావలసిన వృత్త సమీకరణం
x² + y² + 2(\(\frac{1}{3}\)) x + 2(\(\frac{2}{3}\)) y – 5 = 0
⇒ 3(x² + y²) + 2x + 4y – 15 = 0

ప్రశ్న 3.
మూలబిందువు గుండా పోతూ x² + y² – 4x + 2y + 4 = 0 వృత్తాన్ని లంబంగా ఖండిస్తూ, x + y = 4 సరళరేఖపై కేంద్రం కలిగి ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణం
x² + y² + 2gx + 2fy + c = 0
అనుకుందాము.
ఇది మూలబిందువు గుండా పోతుంది కనుక c = 0
ఈ వృత్తం x² + y² – 4x + 2y + 4 = 0 ను లంబంగా ఖండిస్తుంది. కనుక
2(g) (-2) + 2f (+1) = 0 + 4
⇒ – 2g + f = 2 ………………. (1)
కేంద్రం (-g, -f); x + y = 4 రేఖపై ఉన్నది కనుక
(-g) + (- f) = 4 ……………….. (2)
(1), (2) ల నుండి – 3g – 6 ⇒ g = -2
(1) నుండి + 4 + f = 2 ⇒ f = – 2
∴ వృత్త సమీకరణం x² + y² – 4x – 4y = 0

ప్రశ్న 4.
2x² + 2y² + 5x – 6y + 4 = 0 వృత్తానికి లంబంగా ఉంటూ బిందువులు (2, 0), (0, 2) బిందువుల గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0 అనుకుందాం.
ఇది (2, 0), (0, 2) ల గుండా పోతుంది కనుక
4 + 0 + 2g(2) + 2f(0) + c = 0
⇒ 4g + c = – 4 ……………… (1)
0 + 4 + 2g (0) + 2f(2) + c = 0
⇒ 4f + c = – 4 ………………… (2)
(1) – (2) ⇒ 4g – 4f = 0
g = f ………………. (3)
పై వృత్తం x² + y² + \(\frac{5}{2}\)x – 3y + 2 = 0 ను లంబంగా
ఖండిస్తుంది కనుక
2g (\(\frac{5}{4}\)) + 2f (-\(\frac{3}{2}\)) = c + 2
⇒ \(\frac{5g}{2}\) – 3f = 2 + c
⇒ \(\frac{5g}{2}\) – 3g = 2 + c
⇒ – g = 4 + 2c ……………….. (4)
(1) నుండి 4g + c = -4
4(-4 – 2c) + c = -4
-16 – 8c + c =-4
– 7c = 12
c = \(\frac{-12}{7}\)
∴ g = 4+ 2c ……………… (5)
-g = 4 – \(\frac{24}{7}\) = \(\frac{4}{7}\) ⇒ g = \(\frac{-4}{7}\)
∵ g = f = –\(\frac{4}{7}\)
∴ వృత్త సమీకరణం x² + y² – \(\frac{8}{7}\) x – \(\frac{8}{7}\) y – \(\frac{12}{7}\) = 0
⇒ 7(x² + y²) – 8x – 8y – 12 = 0

ప్రశ్న 5.
(2, 3)కేంద్రంగా ఉంటూ x² + y² – 4x + 2y – 7 = 0 వృత్తాన్ని లంబంగా ఖండించే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త వృత్త సమీకరణము
x² + y² – 4x + 2y – 7 = 0 ……………….. (1)
దత్త వృత్తాన్ని లంబంగా ఖండించే వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0 ………………… (2)
కేంద్రం (-g, -f) (2, 3)
g = -2, f = -3
(1), (2) వృత్తాలు లంబంగా ఖండించుకొంటున్నాయి
కాబట్టి 2g₁g₂ + 2f₁f₂ = c₁ + c₂
2(-2) (-2) + 2(-3) (1) = – 7 + c
8 – 6 = -7 + c
+2 = -7 + c
c = 7 + 2 = 9 ⇒ c = 9
∴ కావలసిన వృత్త సమీకరణము
x² + y² – 4x – 6y + 9 = 0

III.

ప్రశ్న 1.
x²+ y² – 6x + 4y – 3 = 0 వృత్తాన్ని లంబంగా ఖండిస్తూ బిందువు (3, 0) గుండా పోతూ Y – అక్షాన్ని స్పృశించే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము (x – h)² + (y – k)² = r² అనుకొందాం
ఈ వృత్తం Y- అక్షాన్ని స్పృశిస్తే కేంద్రం = (h, k);
వ్యాసార్థం = |h|
(x − h)² + (y – k)² = h²
x² – 2hx + h² + y² – 2ky + k² = h².

x² + y² – 6x + 4y – 3 = 0
లంబంగా ఉంది 2(-h) (-3) +2(-k) (2)
= -3 + k²
6h – 4k = -3 + k²

x² – 2hx + y² – 2ky + k² = 0
వృత్తం (3, 0) గుండా పోతుంది
9 – 6h + k² = 0 ………………. (i)
6h – 4k + 3 – k² = 0 ………….. (ii)
(i), (ii) లను కూడగా c = 9
12 – 4k = 0 లేదా k = 3, h = 3
వృత్త సమీకరణము y² + x² – 6x – 6y + 9 = 0

ప్రశ్న 2.
x² + y² – 4x – 6y + 11 = 0, x² + y² – 10x – 4y + 21 = 0 వృత్తాలను లంబంగా ఖండిస్తూ 2x + 3y = 7 వ్యాస రేఖగా గల వృత్త సమీకరణాన్ని కనుక్కోండి. [A.P. Mar 16 (May ’07)]
సాధన:
వృత్తం x² + y² + 2gx + 2fy + c = 0 అనుకుందాం
ఈ వృత్తం x² + y² – 4x – 6y + 11 = 0,
x² + y² – 10x -4y + 21 = 0 లను
లంబంగా ఖండిస్తుంది.
2g (-2) + 2f(-3) = 11 c …………………. (i)
2g (-5) + 2f(-2) = 21 + c ………………. (ii)
తీసివేయగా
-6g+ 2f = 10 ……………….. (iii)
∴ -2g – 3f = 7 ……………….. (iv)
వృత్త కేంద్రం 2x + 3y = 7 మీద ఉంది .
(iii), (iv) లను సాధించగా,
f = -1, g = -2, c = 3
వృత్త సమీకరణము x² + y² – 4x – 2y + 3 = 0

ప్రశ్న 3.
P, Q బిందువులు S ≡ x² + y² + 2gx + 2fy + c = 0 వృత్తం దృష్ట్యా సంయుగ్మబిందువులు అయితే PQ వ్యాసంగా కలిగి ఉండే వృత్తం S = 0 వృత్తాన్ని లంబంగా ఖండిస్తుందని నిరూపించండి.
సాధన:
P = (x₁, y₁), Qx₂, y²) లు క్రింది వృత్తం దృష్ట్యా
సంయుగ్మాలు S ≡ x² + y² – a² = 0 …………. (i)
(i) దృష్ట్యా P యొక్క ధ్రువరేఖ xx₁ + yy₁ – a² = 0 …………… (ii)
P, Qలు సంయుగ్మ బిందువులు Q బిందువు (ii) మీద ఉంటుంది.
x₁x₂ + y₁y₂ – a² = 0 ……………… (iii)
PQ వ్యాసంగా గల వృత్త సమీకరణము
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ x² + y² – (x₁ + x₂)x – (y₁ + y₂)y + (x₁x₂ + y₁y₂) = 0
(i), (iv) లు లంబంగా ఖండించుకొంటే
2g₁g₂ + 2f₁f₂ = 2 \(\left[0\left(\frac{-\left(x_1+x_2\right)}{2}\right)+0\left(\frac{-\left(y_1+y_2\right)}{2}\right)\right]\)
c₁ + c₂ = -a² + a²
⇒ 2g₁g₂ + 2f₁f₂ = c₁ + c₂
∴ PQ వ్యాసంగాగల వృత్తం S వృత్తాన్ని లంబంగా ఖండిస్తుంది.

ప్రశ్న 4.
a, a’ లు వ్యాసార్థాలుగా ఉండే వృత్తాల సమీకరణాలు S = 0, S’ = 0 లు అయితే \(\frac{\mathrm{s}}{\mathrm{a}}+\frac{\mathrm{s}^{\prime}}{\mathrm{a}^{\prime}}\) = 0, \(\frac{\mathrm{s}}{\mathrm{a}}-\frac{\mathrm{s}^{\prime}}{\mathrm{a}^{\prime}}\) = 0 వృత్తాలు లంబంగా ఖండించుకొంటాయని చూపండి.
సాధన.
S = 0, S’ = 0 వృత్తాల కేంద్రాల మధ్య దూరం 2d అనుకుందాం. కేంద్రాలు కలిపే రేఖను X- అక్షంగా, కేంద్రాల మధ్య బిందువును మూల బిందువుగా తీసుకుందాం. వృత్తాల సమీకరణాలు

= 2d²
= (d² – aa’) + (d² + aa’) = c₁ + c₂
∴ (i), (ii) వృత్తాలు లంబంగా ఖండించుకుంటాయి.
కనుక \(\frac{\mathrm{s}}{\mathrm{a}}+\frac{\mathrm{s}^{\prime}}{\mathrm{a}^{\prime}}\) = 0, \(\frac{\mathrm{s}}{\mathrm{a}}-\frac{\mathrm{s}^{\prime}}{\mathrm{a}^{\prime}}\) = 0 వృత్తాలు లంబంగా ఖండించుకుంటాయి.

ప్రశ్న 5.
క్రింద ఇచ్చిన మూడు వృత్తాలలోని ప్రతీ వృత్తాన్ని లంబఛేదనం చేసే వృత్త సమీకరణాన్ని కనుక్కోండి. i) x² + y² + 2x + 4y + 1 = 0;
x² + y² – 2x + 6y – 3 = 0;
2(x² + y²) + 6x + 8y – 3 = 0.
సాధన:
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
దత్త వృత్తము పై 3 వృత్తాలకు లంబంగా ఉంటుంది కనుక
2g(1) + 2f(2) = c + 1 ……………. (i)
2g (\(\frac{9}{2}\)) + 2f(2) = c – \(\frac{3}{2}\) …………….. (ii)
2g(-1) + 2f(3) = c – 3 ……………….. (iii)
(iii) – (ii)
-5g + 2f = \(\frac{-3}{2}\) లేదా -10g + 4f = -3 ………………. (iv)
(iii) – (i)
-4g + 2f = – 4
f – 2g = -2
(iv), (v) లను సాధించగా,
f = -7, g = -5/2, c = -34
∴ వృత్త సమీకరణము
x² + y² – 5x – 14y – 34 = 0

ii) x² + y² + 4x + 2y + 1 = 0;
2(x² + y²) + 8x + 6y – 3 = 0; x² + y² + 6x – 2y – 3 = 0.
సాధన:
కావలసిన వృత్తసమీకరణము
x² + y² + 2gx + 2fy + c = 0
దత్త వృత్తాలు మూడింటికి లంబంగా ఉంటాయి.
∴ 2g(2) + 2f(1) = c + 1 ……………… (i)
2g(2) + 2f (\(\frac{3}{2}\)) = c – \(\frac{3}{2}\) …………… (ii)
2g(3) + 2f(-1) = c – 3 ……………… (iii)
(i) – (ii) చేయగా (ii) – (iii) చేయగా
-f = \(\frac{5}{2}\) అయిన – 2g + 5f = \(\frac{3}{2}\)
g = -7 (∵ f = \(\frac{-5}{2}\))
g. f ల విలువలను (i) లో ప్రతిక్షేపించగా
వృత్త సరణులు
4(-7) + 2 (\(\frac{-5}{2}\)) = = c + 1
c = -34
కావలసిన వృత్త సమీకరణము
x² + y² – 5y – 14x – 34 = 0

ప్రశ్న 6.
2x + 3y = 1 సరళరేఖ x² + y² = 4, A, B బిందువుల వద్ద ఖండిస్తే, AB వ్యాసంగా ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
x² + y² = 4, 2x + 3y − 1 = 0 గుండా పోయే వృత్త సమీకరణము
(x² + y² – 4) + λ (2x + 3y – 1) = 0
x² + y² + 2λx + 3λy – 4 – λ = 0
కేంద్రం : (-λ , \(\frac{-3 \lambda}{2}\))
కేంద్రం 2x + 3y – 1 = 0 మీద ఉంది
∴ 2(-λ) + 3(\(\frac{-3 \lambda}{2}\)) – 1 = 0
λ = \(\frac{-2}{13}\)
∴ వృత్త సమీకరణము
13 (x² + y²) – 4 × 13 – 2(2x + 3y – 1) = 0
13(x² + y²) – 4x – 6y – 50 = 0

ప్రశ్న 7.
x² + y² – 2x + 4y – 8 = 0 AB ఒక జ్యా అయి, దీని సమీకరణం x + y = 3 అయితే AB వ్యాసంగా ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
S = 0, L = 0 ఖండన బిందువుల గుండా పోయే వృత్త
సమీకరణము S + λL = 0
(x² + y² – 2x + 4y – 8) + λ(x + y – 3) = 0
x² + y² + x(-2 + λ) + y(4 + λ) – 8 – 3λ = 0 …………….. (i)
x² + y² + 2gx + 2fy + c = 0 …………….(ii)
(i), (ii) లను పోల్చగా,
g = \(\frac{(-2+\lambda)}{2}\), f = \(\frac{(4+\lambda)}{2}\)
కేంద్రం x + y = 3 మీద ఉంది
∴ \(-\left(\frac{-2+\lambda}{2}\right)-\left(\frac{4+\lambda}{2}\right)\) = 3
2 – λ – 4 – λ = 6
-2λ = 8 ⇒ λ = – 4
కావలసిన వృత్త సమీకరణము
(x² + y² – 2x + 4y – 8) – 4(x + y – 3) = 0
x² + y² – 6x + 4 = 0

ప్రశ్న 8.
x² + y² = 2ax, x² + y² = 2by వృత్తాల ఖండన బిందువులు గుండా పోతూ \(\frac{x}{a}-\frac{y}{b}\) = 2 రేఖపై కేంద్రాన్ని కలిగి ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
x² + y² – 2ax = 0, x² + y² – 2by = 0 ల గుండా పోయే వృత్త సమీకరణము
x² + y² – 2ax +λ(x² + y² – 2by) = 0
x²(1 + λ) + y²(1 + λ) + x(-2a) – (2bλ)y = 0
x² + y² – \(\frac{2 a x}{1+\lambda}\) – \(\frac{2 b y}{1+\lambda}\) = 0
కేంద్రం C \(\left[\frac{a}{1+\lambda}, \frac{b \lambda}{1+\lambda}\right]\)
కేంద్రం \(\frac{x}{a}-\frac{y}{b}\) = 2 మీద ఉంది
\(\frac{+a}{a(1+\lambda)}-\frac{b \lambda}{(1+\lambda) b}\) = 2
1 – λ = 2(1 + λ)
λ = – 1/3
వృత్త సమీకరణము
3x² + 3y² – 6ax – x² – y² + 2by = 0
⇒ 2x² + 2y² – 6ax + 2by = 0
⇒ x² + y² – 3ax + by = 0