Mahesh

AP SCERT 8th Class Maths Textbook Solutions Chapter 12 కారణాంక విభజన Ex 12.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson కారణాంక విభజన Exercise 12.1

ప్రశ్న 1.
ఈ క్రింద ఇచ్చిన పదముల యొక్క సామాన్య కారణాంకములు కనుక్కోండి.
సాధన.
(i) 8x, 24
8x = 2 × 2 × 2 × x
24 = 8 × 3 = 2 × 2 × 2 × 3
∴ 8x, 24 ల సామాన్య కారణాంకాలు = 2, 4, 8

(ii) 3a, 21ab
3a = 3 × a
21ab = 7 × 3 × a × b
∴ 3a, 21ab ల సామాన్య కారణాంకాలు = 3, a, 3a

(iii) 7xy, 35x²y³
7xy = 7 × x × y
35x²y³ = 7 × 5 × x × x × y × y × y
∴ 7xy, 35x²y³ల సామాన్య కారణాంకాలు
= 7, x, y, xy, 7xy, 7x, 7y

(iv) 4m², 6m², 8m³
4m² = 2 × 2 × m × m
6m² = 2 × 3 × m × m
8m² = 2 × 2 × 2 × m × m × m
∴ 4m², 6m², 8m³ల సామాన్య కారణాంకాలు
= 2, m, m², 2m, 2m²

(v) 15p, 20qr, 25rp
15p = 3 × 5 × p
20qr = 4 × 5 × q × r
25rp = 5 × 5 × r × p
∴ 15p, 20qr, 25rpల ఉమ్మడి కారణాంకాలు = 5

(vi) 4x², 6xy, 8y²x
4x² = 2 × 2 × x × x
6xy = 2 × 3 × x × y
8y²x = 2 × 2 × 2 × y × y × x
∴ 4x², 6xy, 8xy²ల సామాన్య కారణాంకాలు
= 2, x, 2x

(vii) 12 x²y, 18 xy²
12x²y = 2 × 2 × 3 × x × x × y
18xy² = 3 × 3 × 2 × x × y × y
∴ 12x²y, 18xy²ల సామాన్య కారణాంకాలు
= 2, 3, 6, x, y, xy, 2x, 2y, 2xy, 3x, 3y, 3xy, 6x, 6y, 6xy

ప్రశ్న 2.
ఈ క్రింది వాటిని కారణాంక విభజన చేయండి.
సాధన.
(i) 5x² – 25xy
= 5 × x × x – 5 × 5 × x × y
= 5 × x[x – 5 × y] = 5x [x – 5y]

(ii) 9a² – 6ax
= 3 × 3 × a × a – 2 × 3 × a × x = 3a[3a – 2x]

(iii) 7p² + 49pq
= 7 × p × p + 7 × 7 × p × q = 7p[p + 7q]

(iv) 36 a²b – 60 a²bc
= 2 × 2 × 3 × 3 × a × a × b – 2 × 2 × 3 × 5 × a × a × b × c
= 2 × 2 × 3 × a × a × b[3 – 5c]
= 12a²b[3 – 5c]

(v) 3a²bc + 6ab²c + 9abc²
= 3 × a × a × b × c + 3 × 2 × a × b × b × c + 3 × 3 × a × b × c × c
= 3abc [a + 2b + 3c]

(vi) 4p² + 5pq – 6pq²
= 2 × 2 × p × p + 5 × p × q – 2 × 3 × p × q × q
= p[4p + 5q – 6q²]

(vii) ut + at²
= u × t – a × t × t
= t[u + at]

ప్రశ్న 3.
ఈ క్రింది వాటికి కారణా౦క విభజన చేయండి.
సాధన.
(i) 3ax – 6ay + 8by – 4bx
= [3ax – 4bx] – [6ay – 8by]
= x[3a – 4b] – 2y [3a – 4b]
= (3a – 4b) [x – 2y]

(ii) x³ + 2x² + 5x + 10
= (x³ + 2x²) + (5x + 10)
= (x² × x + 2 × x²) + [5 × x + 5 × 2]
= x²(x + 2) + 5(x + 2)
= (x + 2)(x² + 5)

(iii) m² – mn + 4m – 4n
= (m² – mn) + (4m – 4n)
= (m × m – m × n) + (4 × m – 4 × n)
= m(m – n) + 4(m – n)
= (m – n) (m + 4)

(iv) a³ – a²b² – ab + b³
= (a³ – a²b²) – (ab – b³)
= (a² × a – a² × b²) – (a × b – b × b²)
= a²(a – b²) – b(a – b²)
= (a – b²) (a² – b)

(v) p²q – pr² – pq + r²
= (p²q – pr²) – (pq – r²)
= (p × p × q – p × r × r) – (p × q – r × r)
= P(pq – r²) – (pq – r²) × 1
= (p – 1) (pq – r²)

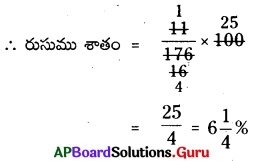
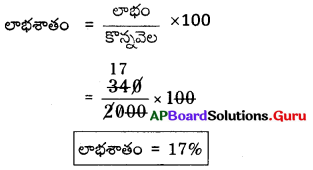
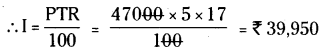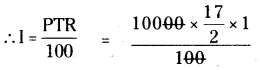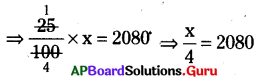AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు InText Questions

ఇవి చేయండి

1. క్రింది బీజీయ సమాసాలలోని పదాల సంఖ్యను తెలుపండి. (పేజీ నెం. 248)
5xy², 5xy³ – 9x, 3xy + 4y – 8, 9x² + 2x + pq + q
సాధన.
5xy² లోని పదాల సంఖ్య 1
5xy³ – 9x లోని పదాల సంఖ్య 2
3xy + 4y – 8 లోని పదాల సంఖ్య 3
9x² + 2x + pq + q లోని పదాల సంఖ్య 4

2. x యొక్క వేర్వేరు విలువలకు 3x + 5 యొక్క విలువ కనుక్కోండి. (పేజీ నెం. 248)
సాధన.
3x + 5
⇒ x = 1 అయిన ⇒ 3x + 5 = 3(1) + 5 = 3 + 5 = 8
⇒ x = 2 అయిన ⇒ 3(2) + 5 = 6 + 5 = 11
⇒ x = 3 అయిన ⇒ 3(3) + 5 = 9 + 5 = 14

3. కింది వాటిలో సజాతి పదాలను గుర్తించంది. (పేజీ నెం. 249)
ax²y, 2x, 5y², – 9x², – 6x, 7xy, 18y².
సాధన.
ax²y, 2x, 5y², – 9x², – 6x, 7xy, 18y².
సజాతి పదాలు : (2x, – 6x), (5y², 18y²)

4. 5pq² కు 3 సజాతి పదాలను తయారుచేయండి. (పేజీ నెం. 249)
సాధన.
5pq² కు సజాతి పదాలు : – 3pq², pq², 1/2pq². మొ||నవి.

5. A = 2y² + 3x – x² , B = 3x² – y² మరియు C = 5x² – 3xy అయితే (పేజీ నెం. 150)

ప్రశ్న (i)
A + B
సాధన.
A = 2y² + 3x – x², B = 3x² – y², C = 5x² – 3xy
A + B = (2y² + 3x – x²) + (3x² – y²)
= (2y² – y²) + 3x + (3x² – x²)
∴ A + B = y² + 3x + 2x²

ప్రశ్న (ii)
A – B
సాధన.
A – B = (2y² + 3x – x²) – (3x² – y²)
= 2y² + 3x – x² – 3x² + y²
∴ A – B = 3y² + 3x – 4x²

ప్రశ్న (iii)
B + C
సాధన.
B + C = (3x² – y²) + (5x² – 3xy)
= 3x² + 5x² – y² – 3xy
∴ B + C = 8x² – y² – 3xy.

ప్రశ్న (iv)
B – C
సాధన.
= (3x² – y²) – (5x² – 3xy)
= 3x² – y² – 5x² + 3xy
∴ B – C = – 2x² – y² + 3xy

ప్రశ్న (v)
A + B + C
సాధన.
= (2y² + 3x – x²) + (8x² – y² – 3xy)
= (2y² – y²) + (8x² – x²) + 3x – 3xy
∴ A + B + C = 7x² + y² + 3x – 3xy

ప్రశ్న (vi)
A + B – C
సాధన.
= (2y² + 3x – x²) + (- 2x² – y² + 3xy)
= (2y² – y²) + (- x² – 2x²) + 3x + 3xy
∴ A + B – C = y² – 3x² + 3x + 3xy

ప్రశ్న 6.
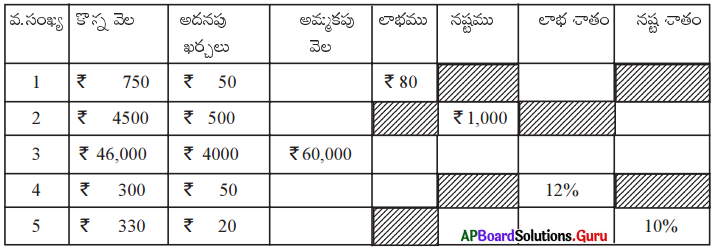
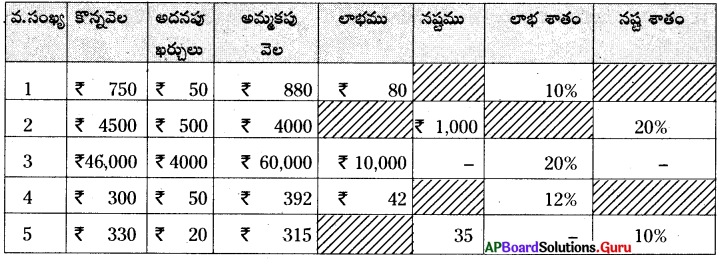
పట్టికను పూర్తి చేయండి. (పేజీ నెం. 253)
సాధన.

7. రెండు ఏక పదుల లబ్ధము ఎల్లప్పుడు ఏకపదియేనా? సరిచూడండి. (పేజీ నెం. 253)
సాధన.
అవును.
ఉదా : 2xy × 5y = 10xy² ఒక ఏకపది.

8. (i) 3x(4ax + 8by)
(ii) 4a²b(a – 3b)
(iii) (p + 3q²)pq
(iv) (m³ + n³) 5mn² లబ్బాలను కనుగొనండి. (పేజీ నెం. 255)
సాధన.
(i) 3x (4ax + 8by) = 3x × 4ax + 3x × 8by
= 12ax² + 24bxy
(ii) 4a²b (a – 3b) = 4a²b × a – 4a²b × 3b
= 4a²b – 12a²b²
(iii) (p + 3q²) pq = p × pq + 3q² × pq
= p²q + 3pq³
(iv) (m³ + n³) 5mn² = m³ × 5mn² + n³ × 5 mn²
= 5 m⁴n² + 5mn⁵

9. ఒక ఏకపది మరియు ఒక బహుపది లబ్దంలో గరిష్టంగా ఏన్ని పదాలుంటాయి?
సాధన.
ఒక ఏకపది మరియు ఒక బహుపదుల లబ్దాలలో అనేక పదాలుంటాయి.

10. లబ్బాలను కనుగొనండి. (పేజీ నెం. 257)

ప్రశ్న (i)
(a – b) (2a + 4b)
సాధన.
= a(22 + 4b) – b(2a + 4b)
= (a × 2a + a × 4b) – (b × 2a + b × 4b)
= 2a² + 4ab – (2ab + 4b²)
= 2a² + 4ab – 2ab – 4b²
= 2a² + 2ab – 4b²

ప్రశ్న (ii)
(3x + 2y) (3y – 4x)
సాధన.
= 3x(3y – 4x) + 2y (3y – 4x)
= 9xy – 12x² + 6y² – 8xy
= xy – 12x² + 6y²

ప్రశ్న (iii)
(2m – l)(2l – m)
సాధన.
= 2m (2l – m) – l(2l – m)
= 2m × 2l – 2m × m – l × 2l + l × m
= 4lm – 2m² – 2l² + lm
= 5lm – 2m² – 2l²

ప్రశ్న (iv)
(k + 3m) (3m – k)
సాధన.
= k(3m – k) + 3m (3m – k)
= k × 3m – k × k + 3m × 3m – 3m × k
= 3m – k² + 9m² – 3km
= 9m² – k²

11. రెండు ద్విపదుల లబ్దములో ఎన్ని పదాలు ఉండును ? (పేజీ నెం. 257)
సాధన.
రెండు ద్విపదుల లబ్దంలో 4 పదాలుండును.
ఉదా : (a + b) (c + d) = ac + ad + bc + bd

12. క్రింద ఇవ్వబడినవి సర్వసమీకరణాలు అవునో, కావో సరిచూడండి. a, b, c లు ధన పూర్ణసంఖ్యలు. (పేజీ నెం. 260)

ప్రశ్న (i)
(a – b) ≡ a² – 2ab + b²
సాధన.
a = 3, b = 1
⇒ (3 – 1)² = (3)² – 2 × 3 × 1 + 1
⇒ (2)² = 9 – 6 + 1
∴ (i) సర్వసమీకరణమే.

ప్రశ్న (ii)
(a + b) (a – b) ≡ a² – b²
సాధన.
a = 2, b = 1
⇒ (2 + 1) (2 – 1) = (2)² – (1)²
⇒ 3 × 1 = 4 – 1
3 = 3
∴ (ii) సర్వసమీకరణమే.

ప్రశ్న (iii)
(a + b + c)² ≡ a² + b² + c² + 2ab + 2bc + 2ca
సాధన.
a = 1, b = 2, c = 0
⇒ (1 + 2 + 0)² = 1² + 2² + 0² + 2 × 1 × 2
+ 2 × 2 × 0 + 2 × 0 × 1
⇒ (3)² = 1 + 4 + 0 + 4 + 0 + 0
⇒ 9 = 1 + 4 + 4 = 9
∴ 9 = 9
∴ (iii) సర్వసమీకరణమే.

13. x = 2, a = 1 మరియు b = 3 విలువలకు (x + a)(x + b) ≡ x² + (a + b) x + ab ను సరిచూడండి. (పేజీ నెం. 260)

ప్రశ్న (i)
LHS = RHS అగునేమో పరిశీలించండి.
సాధన.
(x + a) (x + b) = x² + (a + b) x + ab
x = 2, a = 1, b = 3 అయిన
⇒ (2 + 1) (2 + 3) = 2² + (1 + 3) 2 + 1 × 3
⇒ 3 × 5 = 4 + 4 × 2 + 3
⇒ 15 = 4 + 8 + 3
∴ 15 = 15 ∴ LHS = RHS

ప్రశ్న (ii)
x, a మరియు b యొక్క వివిధ విలువలకు పై సర్వసమీకరణం సరిచూడండి.
సాధన.
x = 0, a = 1, b = 2 అయిన
⇒ (0 + 1) (0 + 2) = 0² + (1 + 2) 0 + 1 × 2
1 × 2= 0 + 0 + 2
∴ 2 = 2
∴ LHS = RHS
∴ x, a, b యొక్క వివిధ విలువలకు LHS = RHS అగును.

ప్రశ్న (iii)
a, b యొక్క అన్ని విలువలకు LHS = RHS అగునా?
సాధన.
a, b యొక్క అన్ని విలువలకు LHS = RHS అగును.

14. (x + p) (x + q) = x² + (p + q)x + pq (పేజీ నెం. 261)

ప్రశ్న (i)
‘p’ బదులుగా ‘q’ ప్రతిక్షేపించండి. ఏమి గమనించారు ?
సాధన.
(x + p) (x + q) = x + (p + q) x + pq లో
pబదులుగా ( ను ప్రతిక్షేపించగా
⇒ (x + q) (x + q) = x² + (q + q) x + q × q
⇒ (x + q) = x² + 24x + q² అగును.

ప్రశ్న (ii)
‘q’ బదులుగా ‘P’ ప్రతిక్షేపించండి. ఏమి గమనించారు ?
సాధన.
q బదులుగా p ను ప్రతిక్షేపించగా
⇒ (x + p) (x + p) = x² + (p + p) x + p × p
⇒ (x + p)² = x² + 2px + p²

ప్రశ్న (iii)
మీరు గమనించిన సర్వసమీకరణాలు ఏవి?
సాధన.
నేను గమనించిన సర్వసమీకరణాలు
(x + q)² = x² + 2qx + q²
(x + p)² = x² + 2px + p²

15. (పేజీ నెం. 261)

ప్రశ్న (i)
(5m + 7n)²
సాధన.
(5m + 7n)² ఇది (a + b)² రూపంలో కలదు.
(a + b)² = a² + 2ab + b² [a = 5m, b = 7n]
(5m + 7n)² = (5m)² + 2 × 5m × 7n + (7n)²
= (5m × 5m) + 70 mn + 7n × 7n
= 25m² + 70mn + 49n²

ప్రశ్న (ii)
(6kl + 7mn)²
సాధన.
(a + b)² = a² + 2ab + b² ప్రకారం
(6kl + 7mn)² = (6kl)² + 2 × 6kl × 7mn +(7mn)²
= 36 k²l² +84 klmn + 49m²n²

ప్రశ్న (iii)
(5a² + 6b²)
సాధన.
a = 5a², b = 6b²
∴ (5a² + 6b²)² = (5a²)² + 2 5a² × 6b² + (6b²)²
= 5a² × 5a² + 60a²b² + 36b⁴
= 25a⁴ + 60a²b² + 36b⁴

ప్రశ్న (iv)
302²
సాధన.
= (300 + 2)²
a = 300, b = 2
∴ (300 + 2)² = (300)² + 2 × 300 × 2 + (2)²
= 300 × 300 + 1200 + 2 × 2
= 90,000 + 1200 + 4
= 91,204

ప్రశ్న (v)
807²
సాధన.
= (800 + 7)²
a = 800, b = 7
(800 + 7)² = (800)² + 2 × 800 × 7 + (7)²
= 800 × 800 + 11,200 + 7 × 7
= 6,40,000 + 11,200 + 49
= 6,51,249

ప్రశ్న (vi)
704² లను విస్తరించండి.
సాధన.
= (700 + 4)²
a = 700, b = 4
∴ (700 + 4)² = (700)² + 2 × 700 × 4 + 4²
= 700 × 700 + 5600 + 4 × 4
= 4,90,000 + 5600 + 16
= 4,95,616

ప్రశ్న (vii)
(a – b)² = a² – 2ab + b² సర్వసమీకరణాన్ని,
a = 3m మరియు b = 5n ఆయినప్పుడు సరిచూడండి.
సాధన.
(a – b)² = a² – 2ab + b² లో a = 3m b = 5nను ప్రతిక్షేపించగా
LHS = (3m – 5n)² = (3m)² – 2 × 3m × 5n + (5n)²
= 9m² – 30mn + 25n²
RHS = (3m)² – 2 × 3m × 5n + (5n)²
= 9m² – 30mn + 25n²
∴ LHS = RHS

16. (పేజీ నెం. 262)

ప్రశ్న (i)
(9m – 2n)²
సాధన.
(9m – 2n)² ఇడి (a – b)² రూపంలో కలదు
(a – b)² = a² – 2ab + b²
(9m – 2n)² = (9m)² – 2 × 9m × 2n + (2n)²
= 9m × 9m – 36mn + 2n × 2n
= 81m² – 36mn + 4n²

ప్రశ్న (ii)
(6pq – 7rs)²
సాధన.
a = 6pq, b = 7rs
∴ [6pq – 7rs]² = (6pq)² – 2 × 6pq × 7rs + (7rs)²
= 6pq × 6pq – 84pqrs + 7rs × 7rs
= 36p²q² – 84pqrs + 49r²s²

ప్రశ్న (iii)
(5x² – 6y²)² లను విస్తరించండి
సాధన.
= (5x²)² – 2 × 5x² × 6y² + (6y²)²
= 5x² × 5x² – 60x²y² + 6y² × 6y²
= 25x⁴ – 60x²y² + 36y⁴

ప్రశ్న (iv)
292²
సాధన.
= (300 – 8)²
a = 300, b= 8
∴ (300 – 8)² = (300)² – 2 × 300 × 8+ (8)²
= 300 × 300 – 4800 + 8 × 8
= 90,000 – 4800 + 64
= 90,064 – 4800 = 85,264

ప్రశ్న (v)
897²
సాధన.
= (900 – 3)²
= (900)² – 2 × 900 × 3 + (3)²
= 8,10,000 – 5400 + 9
= 8,10,009 – 5400 = 8,04,609

ప్రశ్న (vi)
794² ల విలువలు కనుగొనండి
సాధన.
= (800 – 6)²
= (800)² – 2 × 800 × 6 + (6)²
= 6,40,000 – 9600 + 36
= 6,40,036 -9600 = 6,30,436

17.

ప్రశ్న (i)
(6m + 7n) (6m – 7n)
సాధన.
(6m + 7n) (6m – 7n) ఇడి (a + b)(a – b) రూపంలో కలదు.
(a + b)(a – b) = a² – b² ఇక్కడ a = 6m, b = 7m
(6m + 7n) (6m – 7n) = (6m)² – (7n)²
= 6m × 6m – 7n × 7n
= 36m² – 49n²

ప్రశ్న (ii)
(5a + 10b) (5a – 10b)
సాధన.
= (5a)² – (10b)²
[∵ (a + b) (a – b) = a² – b²]
= 5a × 5a – 10b × 10b
= 25a² – 100b²

ప్రశ్న (iii)
(3x² + 4y²) (3x² – 4y²) ల విలువలు కనుక్కొండి.
సాధన.
= (3x²)² – (4y²)²
[∵ (a + b)(a – b) = a² – b²]
= 3x² × 3x² – 4y² × 4y²
= 9x⁴ – 16y⁴

ప్రశ్న (iv)
106 × 94
సాధన.
= (100 + 6) (100 – 6)
= 100² – 6²
[∵ (a + b)(a – b) = a² – b²)
= 100 × 100 – 6 × 6
= 10,000 – 36 = 9,964

ప్రశ్న (v)
592 × 608
సాధన.
= (600 – 8) (600 + 8)
= (600)² – (8)² [∵ (a + b) (a – b) = a² – b²) = 600 × 600 – 8 × 8
= 3,60,000 – 64
= 3,59,936

ప్రశ్న (vi)
92² – 8²
సాధన.
ఇది a² – b² = (a + b)(a – b) రూపంలో కలదు.
92² – 8² = (92 + 8) (92 – 8)
= 100 × 84
= 8400

ప్రశ్న (vii)
984² – 16² లను సూక్ష్మీకరించండి.
సాధన.
= (984 +16) (984 – 16)
[∵ a² – b² = (a + b)(a – b)]
= (1000) (968)
= 9,68,000

ప్రయత్నించండి

1. వేగము, కాలము ఉపయోగించి దూరము లెక్కించు నప్పుడు, అసలు, రేటు కాలము ఇచ్చినప్పుడు సామాన్య వడ్డీ లెక్కించుటకు బీజీయ సమాసములు వ్రాయుము. బీజీయ సమాసములు ఉపయోగించి విలువలు కనుగొను మరొక రెండు సందర్భములు తెలపండి. (పేజీ నెం. 251)
సాధన.
d = s × t (లేదా) దూరం = వేగం × కాలం
I = \(\frac {PTR}{100}\) (లేదా)
సామాన్య వడ్డీ = \(\frac {అసలు × వడ్డీ రేటు × కాలం}{100}\)
బీజీయ సమాసాలనుపయోగించే రెండు సందర్భాలు :
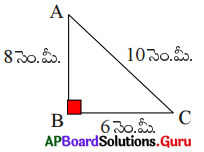
(i) త్రిభుజ వైశాల్యం = \(\frac {1}{2}\) × భూమి × ఎత్తు
= \(\frac {1}{2}\)bh
(ii) దీర్ఘ చతురస్ర చుట్టుకొలత = 2(పొడవు + వెడల్పు)
= 2(l+ b)

ఆలోచించి, చర్చించి వ్రాయండి

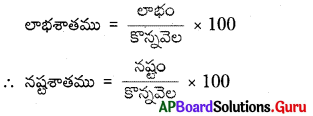
1. షీలా 2pq, 4pq ల మొత్తం 8p² q² అని చెప్పింది. సమాధానం సరైందా ? మీ వివరణ ఇవ్వండి. (పేజీ నెం. 249)
సాధన.
2pq, qpq ల మొత్తము = 2pq + 4pg = 6pq.
కానీ షీలా సమాధానం ప్రకారం పై రెండింటి మొత్తం 8p²q²
∴ 8p²q² ≠ 6pq
∴ ఆమె (షీలా) సమాధానం సరియైనది కాదు.

2. రెహమాన్ 4x ను 7yలకు కలిపితే 11xy వస్తుందన్నాడు. మీరు ఏకీభవిస్తారా ? (పేజీ నెం. 249)
సాధన.
4x, 7y ల మొత్తం ≠ 4x + 7y
రెహమాన్ ప్రకారం పై రెండు పదాల మొత్తం = 11xy
∴ 11xy ≠ 4x + 7y
∴ నేను రెహమాన్ సమాధానంతో ఏకీభవించను.

AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు Ex 11.5 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు Exercise 11.5

1. (a + b)² = a² + 2ab + b² ను జ్యామితీయంగా a, bల క్రింది విలువలకు సరిచూదండి.

ప్రశ్న (i)
a= 2 యూనిట్లు, b = 4 యూనిట్లు
సాధన.
(a + b)² ≡ a² + 2ab + b²
⇒ (2 + 4)² ≡ 2² + 2 × 2 × 4 + (4)²
⇒ (6)² ≡ 4 + 16 + 16
⇒ 36 ≡ 36
∴ LHS ≡ RHS

ప్రశ్న (ii)
a = 3 యూనిట్లు, b = 1 యూనిట్
సాధన.
(a + b)² ≡ a² + 2ab + b²
⇒ (3 + 1)² ≡ (3)² + 2 × 3 × 1 + (1)²
⇒ 4² ≡ 9 + 6 + 1
⇒ 16 ≡ 16
∴ LHS ≡ RHS

ప్రశ్న (iii)
a = 5 యూనిట్లు, b= 2 యూనిట్లు
సాధన.
(a + b)² ≡ a² + 2ab + b²
⇒ (5 + 2)² ≡ (5)² + 2 × 5 × 2 + (2)²
⇒ 7² ≡ 25 + 20 + 4
⇒ 49 ≡ 49
∴ LHS ≡ RHS

2. (a – b)² = a² – 2ab + b² ను జ్యా మితీయంగా a, bల క్రింది విలువలకు సరిచూడండి.

ప్రశ్న (i)
a = 3 యూనిట్లు, b = 1 యూనిట్
సాధన.
(a – b)² ≡ a² – 2ab + b²
⇒ (3 – 1)² ≡ (3)² – 2 × 3 × 1 + (1)²
⇒ (2)² ≡ 9 – 6 + 1 = 10 – 6
⇒ 4 ≡ 4
∴ LHS ≡ RHS

ప్రశ్న (ii)
a = 5 యూనిట్లు, b = 2 యూనిట్లు
సాధన.
(a – b)² ≡ a² – 2ab + b²
⇒ (5 – 2)² ≡ (5)² – 2 × 5 × 2 + (2)²
⇒ (3)² ≡ 25 – 20 + 4 = 29 – 20
⇒ 9 ≡ 9
∴ LHS ≡ RHS

3. (a + b) (a – b) ≡ a² – b²ను జ్యా మితీయంగా a, bల క్రింది విలువలకు సరిచూడండి.

ప్రశ్న (i)
a = 3 యూనిట్లు, b = 2 యూనిట్లు
సాధన.
⇒ (a + b) (a – b) ≡ a² – b²
⇒ (3 + 2) (3 – 2) ≡ 3² – 2²
⇒ 5 × 1 ≡ 9 – 4
⇒ 5 ≡ 5
∴ LHS = RHS

ప్రశ్న (ii)
a = 2 యూనిట్లు, b =1 యూనిట్
సాధన.
⇒ (a + b) (a – b) ≡ a² – b²
⇒ (2 + 1) (2 – 1) ≡ (2)² – (1)²
⇒ 3 × 1 ≡ 4 – 1
⇒ 3 ≡ 3
∴ LHS ≡ RHS

AP SCERT 8th Class Maths Textbook Solutions Chapter 11 బీజీయ సమాసాలు Ex 11.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson బీజీయ సమాసాలు Exercise 11.4

1. కింది సమస్యలకు తగిన “సర్వసమీకరణాలను” (Identities) సూచించింది. లబ్ధము కనుగొనండి.

ప్రశ్న (i)
(3k + 4l) (3k +4l)
సాధన.
= (3k + 4l)² ఇది (a + b)² రూపంలో కలదు.
= (3k)² + 2 × 3k × 4l + (4l)² [∵ (a + b)² = a² + 2ab + b²]
= 3k × 3k + 24kl + 4l × 4l
= 9k² + 24kl + 16l²

ప్రశ్న (ii)
(ax² + by²) (ax² + by²)
సాధన.
= (ax² + by²)² ఇది (a + b)² రూపంలో కలదు.
= (ax²)² + 2 × ax² × by² + (by²)² [∵ (a + b)² = a² + b² + 2ab]
= ax² × ax² + 2abx²y² + by² × by²
= a²x⁴ + 2abx²y² + b²y⁴

ప్రశ్న (iii)
(7d – 9e) (7d – 9e)
సాధన.
= (7d – 9e)², ఇది (a – b)² రూపంలో కలదు.
= (7d)² – 2 × 7d × 9e + (9e)² [∵ (a – b)² = a² – 2ab + b²]
= 7d × 7d – 126de + 9e × 9e
= 49d² – 126de + 81e²

ప్రశ్న (iv)
(m² – n²) (m² + n²)
సాధన.
(m² – n²) (m² + n²) ఇది (a + b) (a – b) రూపంలో కలదు.
∴ (m² + n²) (m² – n²) = (m²)² – (n²)² = m⁴ – n⁴ [∵ (a + b)(a – b) = a² – b²

ప్రశ్న (v)
(3t + 9s) (3t – 9s)
సాధన.
(3t + 9s) (3t – 9s) = (3t)² – (9s)² [∵ (a + b)(a – b) = a² – b²

ప్రశ్న (vi)
(kl – mn) (kl + mn)
సాధన.
= kl × kl – mn × mm
= k²l² – m²n²

ప్రశ్న (vii)
(6x + 5) (6x + 6)
సాధన.
(6x + 5) (6x + 6)
ఇది (ax + b) (ax + c) రూపంలో కలదు.
(ax + b) (ax + c) = a²x² + ax (b + c) + bc
(6x + 5) (6x + 6) = (6)²x² + 6x (5 + 6) +5 × 6
= 36x² + 6x × 11 + 30
= 36x² + 66x + 30

ప్రశ్న (viii)
(2b – a) (2b + c)
సాధన.
ఇది (ax – b) (ax + c) రూపంలో కలదు.
(ax – b) (ax + c) = a²x² + ax (c – b) – cb
(2b – a) (2b + c) = (2)²b² + 2b (c – a) – ca
= 4b² + 2bc – 2ab – ca

2. కింది వాటికి తగిన సర్వసమీకరణాలను ఉపయోగించి విలువలను కనుగొనండి.

ప్రశ్న (i)
304²
సాధన.
= (300 + 4)², ఇది (a + b)² రూపంలో కలదు.
(a + b)² = a² + 2ab + b²
a = 300, b = 4
(300 + 4)² = (300)² + 2 × 300 × 4 + (4)²
= 300 × 300 + 24000 + 4 × 4
= 90,000 + 2400 + 16 = 92,416

ప్రశ్న (ii)
509²
సాధన.
= (500 + 9)² a = 500, b = 9
= (500)² + 2 × 500 × 9 + (9)²
= 500 × 5000 + 9000 + 9 × 9
= 2,50,000 + 90000 + 81
= 2,59,081

ప్రశ్న (iii)
992²
సాధన.
= (1000 – 8)² a = 1000, b = 8
= (1000)² – 2 × 1000 × 8 + (8)²
= 10000 × 1000 – 16,000 + 8 × 8
= 10,00,000 – 16000 + 64
= 10,00,064 – 1600
= 9,98,464

ప్రశ్న (iv)
799²
సాధన.
= (800 – 1)² a = 800, b = 1
= (800)² – 2 × 800 × 1 + (1)²
= 800 × 800 – 1600 + 1
= 6,40,000 – 1600 + 1
= 6,40,001 – 1600
= 6,38,401

ప్రశ్న (v)
304 × 296
సాధన.
= (300 + 4) (300 – 4),
ఇది (a + b) (a – b) రూపంలో కలదు.
(a + b) (a – b) = a² – b²
(300 + 4) (300 – 4) = (300)² – (4)²
=300 × 300 – 4 × 4
= 90,000 – 16
= 89,984

ప్రశ్న (vi)
83 × 77
సాధన.
= (80 + 3) (80 – 3)
= (80)² – (3)² [∵ (a + b) (a – b) = a² – b²]
= 80 × 80 – 3 × 3
= 6400 – 9
= 6391

ప్రశ్న (vii)
109 × 108
సాధన.
= (100 + 9) (100 + 8)
= (100) + (9 + 8) 100 + 9 × 8
= 10,000 + 1700 + 72
= 11,772

ప్రశ్న (viii)
204 × 206
సాధన.
= (205 – 1) (205 + 1)
= (205)² – (1)²
= 205 × 205 – 1 x 1
= 42,025 – 1
= 42,024

SCERT AP 8th Class Maths Solutions Chapter 6 వర్గమూలాలు, ఘనమూలాలు Ex 6.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 6th Lesson వర్గమూలాలు, ఘనమూలాలు Exercise 6.4

ప్రశ్న1.
క్రింది సంఖ్యల ఘనాలు కనుగొనుము.
(i) 8
(ii) 16
(iii) 21
(iv) 30
సాధన.

ప్రశ్న2.
క్రింది సంఖ్యలు సంపూర్ణ ఘనాలా ? కాదా ? పరీక్షించండి.
(i) 243
(ii) 516
(iii) 729
(iv) 8000
(v) 2700
సాధన.

ప్రశ్న3.
8788 ను ఏ కనిష్ఠ సంఖ్యచే గుణించిన సంపూర్ణ ఘనసంఖ్య అగును ?
సాధన.

8788 యొక్క ప్రధాన కారణాంకాల లబ్దం = (2 × 2) × (13 × 13 × 13)
పై లబ్దాల త్రికములలో ‘2’ లోపించినది
కావునా 8788ను 2 అనే కనిష్ఠ సంఖ్యచే గుణించిన అది సంపూర్ణ ఘనసంఖ్య అగును.

ప్రశ్న4.
7803 ను ఏ కనిష్ఠ సంఖ్యచే గుణించిన వచ్చు లబ్ధం సంపూర్ణ ఘనం అగును ?
సాధన.

7803 యొక్క ప్రధాన కారణాంకాల లబ్దం = (3 × 3 × 3) × (17 × 17)
∴ పై లబ్దంలో ఒక ’17’ లోపించినది కావునా 7803 ను ’17’ చే గుణించిన అది సంపూర్ణ ఘనం అగును.

ప్రశ్న5.
8640ని ఏ కనిష్ఠ సంఖ్యచే భాగించిన వచ్చు భాగఫలం సంపూర్ణ ఘనం అగును ?
సాధన.

8640 యొక్క ప్రధాన కారణాంకాల లబ్ధం
= (2 × 2 × 2) × (2 × 2 × 2) × 5 × (3 × 3 × 3)
= 2³ × 2³ × 5 × 3³
∴ 8640 ఒక సంపూర్ణ ఘనసంఖ్య కావలెనన్న దానిని ‘5’ చే భాగింపవలెను.

ప్రశ్న6.
రవి ప్లాస్టసీన్ (మైనము) తో చేసిన ప్రమాణ ఘనాలను ఉపయోగించి 12 సెం.మీ., 8 సెం.మీ. మరియు 3 సెం.మీ. కొలతలు గల దీర్ఘ ఘనాన్ని తయారు చేసెను. అతడు తయారీకి కనీసం ఎన్ని ప్రమాణ ఘనాలను ఉపయోగించెను ?
సాధన.
12 సెం.మీ. × 8 సెం.మీ. × 3 సెం.మీ. కొలతలు గల దీర్ఘఘనం ఘనపరిమాణం = l × b × h
= 12 × 8 × 3
= 288 సెం.మీ.³
288 సెం.మీ.³ ఘనపరిమాణంతో తయారుచేయగల ప్రమాణ ఘనాల ఘనపరిమాణం దీనికంటే తక్కువ లేదా సమానంగా ఉండవలెను. అది 216 సెం.మీ.³ అవుతుంది.
∴ s³ = 216 అయిన
s = \(\sqrt[3]{216}\) = \(\sqrt[3]{6^{3}}\) = 6 సెం.మీ.

ప్రశ్న7.
3¹¹ + 5¹³ మొత్తాన్ని భాగించగలుగు కనిష్ఠ ప్రధాన సంఖ్యను కనుగొనుము.
సాధన.
3¹¹ + 5¹³ నుండి

∴ 3¹¹ యొక్క విస్తరణలో ఒకట్ల స్థానంలోని అంకె = 7
5¹³ యొక్క లబ్దంలో ఒకట్ల స్థానంలోని అంకె = 5
∴ 7 + 5 = 12 ను భాగించగల కనిష్ఠ ప్రధాన సంఖ్య = 2

SCERT AP 8th Class Maths Solutions Chapter 6 వర్గమూలాలు, ఘనమూలాలు Ex 6.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 6th Lesson వర్గమూలాలు, ఘనమూలాలు Exercise 6.3

ప్రశ్న1.
భాగహార పద్ధతిన వర్గమూలాలు కనుక్కోండి.
(i) 1089
సాధన.

∴ \(\sqrt{1089}\) = 33

(ii) 2304
సాధన.

∴ \(\sqrt{2304}\) = 48

(iii) 7744
సాధన.

∴ \(\sqrt{7744}\) = 88

(iv) 6084
సాధన.

∴ \(\sqrt{6084}\) = 78

(v) 9025
సాధన.

∴ \(\sqrt{6084}\) = 78

ప్రశ్న2.
క్రింది దశాంశాలకు వర్గమూలాలను కనుక్కోండి.
(i) 2.56
సాధన.

∴ \(\sqrt{2.56}\) = 78

(ii) 18.49
సాధన.

∴ \(\sqrt{18.49}\) = 4.3

(iii) 68.89
సాధన.

∴ \(\sqrt{68.89}\) = 8.3

(iv) 84.64
సాధన.

∴ \(\sqrt{84.64}\) = 9.2

ప్రశ్న3.
4000 నుండి ఏ కనిష్ఠ సంఖ్యను తీసివేసిన పరిపూర్ణ వర్గం అగును ?
సాధన.
4000 నుండి ఒక కనిష్ఠ సంఖ్యను తీసివేయవలెనన్న భాగహార పద్ధతిన వర్గమూలం కనుగొనవలె.

∴ 4000 నుండి ’31’ అను కనిష్ఠ సంఖ్యను తీసివేసిన పరిపూర్ణ వర్గం అగును.

ప్రశ్న4.
ఒక చతురస్ర వైశాల్యం 4489 సెం.మీ.² అయిన భుజం పొడవు ఎంత ?
సాధన.
చతురస్ర వైశాల్యం (A) = 4489 సెం.మీ.²
∴ A = s²
⇒ s² = \(\sqrt{4489}\) = \(\sqrt{67 \times 67}\) = 67 సెం.మీ.
చతురస్ర భుజం (s) = 67 సెం.మీ.

ప్రశ్న5.
ఒక తోటమాలి 8289 మొక్కలను చతురస్రాకారంలో కొన్ని వరుసలలో నాటాడు. నాటిన తరువాత 8 మొక్కలు మిగిలిన ప్రతి వరుసలో నాటిన మొక్కలు ఎన్ని ?
సాధన.
మొత్తం నాటిన మొక్కలు = 8289
8289 మొక్కలను చతురస్రాకారంలో నాటగా 8మొక్కలు మిగిలిపోగా నాటిన మొక్కలు = 8289 – 8
= 8281
ఒక్కొక్క వరుసలో నాటిన మొక్కల సంఖ్య కావలెనన్న 8281 కు వర్గమూలం కనుగొనవలెను.

∴ 8281 మొక్కలను చతురస్రాకారంగా నాటగా ప్రతి వరుసకు వచ్చు మొక్కల సంఖ్య = 91

ప్రశ్న6.
కనిష్ఠ నాలుగు అంకెల పరిపూర్ణ వర్గ సంఖ్యను కనుగొనుము.
సాధన.
నాలుగు అంకెల కనిష్ఠ సంఖ్య = 1000

∴ 1000 కు 24 ను కలిపిన 1000 + 24 = 1024
∴ నాలుగు అంకెల కనిష్ఠ పరిపూర్ణ వర్గసంఖ్య = 1024

ప్రశ్న7.
6412 కు ఏ కనిష్ఠ సంఖ్యను కలిపిన పరిపూర్ణ వర్గసంఖ్య అగును ?
సాధన.

∴ 6412 కు 149 అను కనిష్ఠ సంఖ్యను కలిపిన పరిపూర్ణ వర్గసంఖ్య అగును.

ప్రశ్న8.
క్రింది వాటి వర్గమూలాలను దగ్గరి పూర్ణాంకానికి అంచనా వేసి చెప్పండి.
(i) \(\sqrt{97}\)
సాధన.
97, వర్గ సంఖ్యలయిన 81 మరియు 100 ల మధ్య ఉండును.
81 < 97 < 100
⇒ 9² < 97 < 10²
⇒ 9 < \(\sqrt{97}\) < 10
∴ \(\sqrt{97}\) విలువ 10 కి. దగ్గరగా ఉండవచ్చు.
[∵ 97, 100 కు దగ్గరగా ఉన్నది.]

(ii) \(\sqrt{250}\)
సాధన.
250 వర్గ సంఖ్యలైన 225, 256 ల మధ్య ఉండును.
∴ 225 < 250 < 256
⇒ 15² < 250 < 16²
= 15 < \(\sqrt{250}\) < 16
∴ 250 విలువ 16 కు దగ్గరగా ఉండవచ్చు.
[∵ 250, 256 కు దగ్గరగా ఉన్నది.]

(iii) \(\sqrt{780}\)
సాధన.
780, వర్గ సంఖ్యలైన 729 మరియు 784 ల మధ్య కలదు.
∴ 729 < 780 < 784
⇒ 27² < 780 < 28²
⇒ 27 < \(\sqrt{780}\) < 28
∴ \(\sqrt{780}\), 28 కు దగ్గరగా ఉండును.
[∵ 780, 784 కు దగ్గరగా ఉన్నది.]

SCERT AP 8th Class Maths Solutions Chapter 6 వర్గమూలాలు, ఘనమూలాలు Ex 6.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 6th Lesson వర్గమూలాలు, ఘనమూలాలు Exercise 6.2

ప్రశ్న1.
ప్రధాన కారణాంకాల పద్ధతిని ఉపయోగించి క్రింది వాటి వర్గమూలాలు కనుగొనుము.
(i) 441
(ii) 784
(iii) 4096
(iv) 7056
సాధన.

ప్రశ్న2.
3645 ని ఏ కనిష్ఠ సంఖ్యచే గుణించిన పరిపూర్ణ వర్గం అగును ?
సాధన.
3645 యొక్క ప్రధాన కారణాంకాల లబ్దం = (3 × 3) × 5 × (3 × 3) × (3 × 3)

ఒక ‘5’ లోపించినది కావునా
3645 ను 5చే గుణించిన పరిపూర్ణ వర్గం అగును.

ప్రశ్న3.
2400 ని ఏ కనిష్ఠ సంఖ్యచే గుణించగా పరిపూర్ణ వర్గం అగును ? వచ్చిన ఫలిత సంఖ్య వర్గమూలం కనుగొనుము.
సాధన.
2400 యొక్క ప్రధాన కారణాంకాల లబ్దం
= (2 × 2) × (2 × 2) × 2 × (5 × 5) × 3
∴ పై లబ్దాల జతలలో 2, 3లు లోపించినవి కావునా 2 × 3 = 6 చే గుణించగా 2400 పరిపూర్ణ వర్గ సంఖ్య అగును.

∴ 2400 × 6 = (2 × 2) × (2 × 2) × (2 × 2) × (5 × 5) × (3 × 3)
⇒ \(\sqrt{14400}\) = 2 × 2 × 2 × 5 × 3
= 120

ప్రశ్న4.
7776 ను ఏ కనిష్ఠ సంఖ్యచే భాగించగా పరిపూర్ణ వర్గం అగును ?
సాధన.
7776 యొక్క ప్రధాన కారణాంకాల లబ్దం

= (2 × 2) × (2 × 2) × 2 × (3 × 3) × (3 × 3) × 3
∴ 7776 పరిపూర్ణ వర్గ సంఖ్య.
కావలెనన్న దానిని 2 × 3 = 6 చే భాగించవలెను.

ప్రశ్న5.
ఒక తోటలో ఉన్న 1521 చెట్లు కొన్ని వరుసలలో కలవు. ప్రతి వరుసలో ఉన్న చెట్ల సంఖ్య, వరుసల సంఖ్యకు సమానం. అయిన ప్రతి వరుసలోని చెట్ల సంఖ్య, తోటలోని వరుసల సంఖ్య కనుక్కోండి.
సాధన.
తోటలోని ఒక్కొక్క వరుసలో ఉన్న చెట్ల సంఖ్య = x అనుకొనుము.
తోటలోని వరుసల సంఖ్య = x
తోటలో గల మొత్తం చెట్ల సంఖ్య = x × x = x²
లెక్క ప్రకారం తోటలో గల చెట్ల సంఖ్య = 1521
∴ x² = 1521
x = \(\sqrt{1521}\) = \(\sqrt{39 \times 39}\) = 39
∴ ఆ తోటలోని ఒక్కొక్క వరుసకు గల చెట్ల సంఖ్య = 39
∴ ఆ తోటలోని వరుసల సంఖ్య = 39

ప్రశ్న6.
ఒక పాఠశాలలో విద్యార్థుల నుండి ఫీజు రూపంలో ₹ 2601 వసూలు చేశారు. పాఠశాలలోని విద్యార్థుల సంఖ్య, ప్రతి విద్యార్థి చెల్లించిన ఫీజుకి సమానం అయిన విద్యార్థుల సంఖ్య ఎంత ?
సాధన.
పాఠశాలలోని విద్యార్థుల సంఖ్య = x అనుకొనుము.
ప్రతి విద్యార్థి చెల్లించిన ఫీజు = ₹ x
∴ పాఠశాల మొత్తం మీద వసూలైన ఫీజు x × x = x²
లెక్క ప్రకారం
పాఠశాలకు ఫీజు రూపంలో వచ్చినది = 2601
∴ x² = 2601
∴ x = \(\sqrt{2601}\) = \(\sqrt{51 \times 51}\) = 51
∴ ఆ పాఠశాలలోని విద్యార్థుల సంఖ్య = 51

ప్రశ్న7.
రెండు సంఖ్యల లబ్ధం 1296. వాటిలో మొదటి సంఖ్య, రెండవ సంఖ్యకు 16 రెట్లు అయిన ఆ రెండు సంఖ్యలు ఏవి?
సాధన.
రెండవ సంఖ్య = x అనుకొనుము.
మొదటి సంఖ్య = 16x
రెండు సంఖ్యల లబ్దం = 16 x × x = 16x²
లెక్క ప్రకారం
⇒ 16x² = 1296

x² = 81
x = \(\sqrt{81}\) = \(\sqrt{2601}\) = 9
∴ మొదటి సంఖ్య = 16x = 16 × 9 = 144
రెండవ సంఖ్య (x) = 9

ప్రశ్న8.
7921 మంది సైనికులు ఒక సమావేశమందిరం (ఆడిటోరియం) లో కొన్ని వరుసలలో కూర్చొని ఉన్నారు. ప్రతి వరుసలోని సైనికుల సంఖ్య, వారు కూర్చున్న వరుసల సంఖ్యకు సమానం. అయిన సమావేశమందిరంలో ఉన్న వరుసల సంఖ్య ఎంత?
సాధన.
ప్రదర్శనశాలలోని సైనికుల సంఖ్య = x అనుకొనుము.
సైనికులు కూర్చొను వరుసల సంఖ్య = x
మొత్తం సైనికుల సంఖ్య = x × x = x²
లెక్క ప్రకారం
x² = 7921
x = \(\sqrt{7927}\) = \(\sqrt{89 \times 89}\) = 89
∴ ఆ సమావేశమందిరంలోని వరుసల సంఖ్య = 89

ప్రశ్న9.
ఒక చతురస్రాకార పొలం వైశాల్యం 5184 మీ². చతురస్రపు చుట్టుకొలతకు సమాన చుట్టుకొలత గల దీర్ఘచతురస్రం కలదు. దీర్ఘ చతురస్రం యొక్క పొడవు, వెడల్పుకు రెట్టింపు అయిన దీర్ఘచతురస్ర వైశాల్యం ఎంత ?
సాధన.
చతురస్ర వైశాల్యం = 5184
A = s² = 5184
⇒ s = \(\sqrt{5184}\) = \(\sqrt{72 \times 72}\) = 72
∴ చతురస్ర భుజం (s) = 72 మీ.
చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 72 = 288 మీ.
దీర్ఘచతురస్ర చుట్టుకొలత = చతురస్ర చుట్టుకొలత
దీర్ఘ చతురస్ర వెడల్పు = x మీ. అనుకొనుము.
పొడవు = 2 × x = 25 మీ.
దీ॥చ॥ చుట్టుకొలత = 2(l + b)
⇒ 2(2x + x) = 288
3x = 144
x = 48
∴ దీర్ఘచతురస్ర వెడల్పు = 48 మీ.
పొడవు = 2x = 2 × 48 = 96 మీ.
∴ దీర్ఘచతురస్ర వైశాల్యం = పొడవు × వెడల్పు
= 96 × 48
= 4608 మీ².

SCERT AP 8th Class Maths Solutions Chapter 6 వర్గమూలాలు, ఘనమూలాలు Ex 6.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 6th Lesson వర్గమూలాలు, ఘనమూలాలు Exercise 6.1

ప్రశ్న1.
క్రింది సంఖ్యల వర్గాలలో, ఒకట్ల స్థానంలోని అంకెలేవి ?
(i) 39
(ii) 297
(iii) 5125
(iv) 7286
(v) 8742
సాధన.

ప్రశ్న2.
క్రింది సంఖ్యలలో పరిపూర్ణ వర్గాలు ఏవి ?
(i) 121
(ii) 136
(iii) 256
(iv) 321
(v) 600
సాధన.

ప్రశ్న3.
క్రింది సంఖ్యలు, పరిపూర్ణ వర్గాలు కావు. కారణాలు తెల్పండి.
(i) 257
(ii) 4592
(iii) 2433
(iv) 5050
(v) 6098
సాధన.
(i) 257 → వర్గంలో ఒకట్ల స్థానంలోని అంకె 7. కావున ఇది పరిపూర్ణ వర్గసంఖ్య కాదు.
(ii) 4592 → వర్గంలో ఒకట్ల స్థానంలోని అంకె 2. కావున ఇది పరిపూర్ణ వర్గ సంఖ్య కాదు.
(iii) 2433 → వర్గసంఖ్యలో ఒకట్ల స్థానంలోని అంకె 3. కావున ఇది పరిపూర్ణ వర్గసంఖ్య కాదు.
(iv) 5050 → వర్గంలో ఒకట్ల స్థానంలోని అంకె ‘0’ అయిన చివరి రెండంకెలు (0) సున్నాలై ఉండాలి.
∴ కాబట్టి ఇది కూడా పరిపూర్ణ వర్గసంఖ్య కాదు.
(v) 6098 → వర్గంలో ఒకట్ల స్థానంలోని అంకే 8. కావున ఇది పరిపూర్ణ వర్గసంఖ్య కాదు.

ప్రశ్న4.
క్రింది సంఖ్యల వర్గాలు సరిసంఖ్యలా ? లేదా బేసిసంఖ్యలా ?
(i) 431
(ii) 2826
(iii) 8204
(iv) 17779
(v) 99998
సాధన.

ప్రశ్న5.
క్రింది సంఖ్యల వర్గాల మధ్య ఎన్ని పూర్ణసంఖ్యలు ఉంటాయి ?
(i) 25, 26
(ii) 56, 57
(iii) 107, 108
సాధన.
(i) 25, 26 → 2 × 25 = 50
(ii) 56, 57 → 2 × 56 = 112
(iii) 107, 108 → 2 × 107 = 214
పూర్ణాంకాలుంటాయి.

ప్రశ్న6.
కూడకుండానే కింది వాటి మొత్తాన్ని కనుగొనండి.
(i) 1 + 3 + 5 + 7 + 9 =
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 =
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 =
సాధన.
(i) 1 + 3 + 5 + 7 + 9 = (5)² = 5 × 5 = 25
ఎందుకనగా మొదటి 5 వరుస బేసిసంఖ్యల మొత్తం 5² కు సమానం అగును.
అదే విధంగా మొదటి n బేసి సంఖ్యల మొత్తం = n² అగును.
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17
= 9² = 81 (∵ n = 9)
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 = 132 = 13 × 13 = 169 (∵ n = 13)

SCERT AP 8th Class Maths Solutions Chapter 5 అనుపాతముతో రాశులను పోల్చుట InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson అనుపాతముతో రాశులను పోల్చుట InText Questions

ఇవి చేయండి

1. ₹ 20,000 లపై 5% వడ్డీరేటు చొప్పున 6 సంవత్సరములకు వడ్డీ సంవత్సరమున కొకసారి తిరిగి లెక్కకట్టగా వచ్చే చక్రవడ్డీ ఎంత ? (పేజీ నెం. 114)
సాధన.
P = ₹ 20,000; R = 5%; n = 6 సం॥లు.
A = \(P\left[1+\frac{R}{100}\right]^{n}\)
= \(20000\left[1+\frac{5}{100}\right]^{6}\)
= \(20000 \times\left(1+\frac{1}{20}\right)^{6}\)
= \(20000 \times\left(\frac{21}{20}\right)^{6}\)
= \(20000 \times \frac{21 \times 21 \times 21 \times 21 \times 21 \times 21}{20 \times 20 \times 20 \times 20 \times 20 \times 20}\)
= 26801.9
A = ₹ 26802
∴ చక్రవడ్డీ = మొత్తం – అసలు
= 26802 – 20,000 = ₹ 6802/-

2. ₹ 12,600 లపై 10% వడ్డీరేటు చొప్పున 2 సంవత్సరములకు వడ్డీ సంవత్సరమున కొకసారి లెక్కకట్టగా వచ్చే చక్రవడ్డీ ఎంత ? (పేజీ నెం. 114)
సాధన.
P = ₹ 12,600; R = 10%; n = 2 సం॥లు.
∴ A = \(\mathrm{P}\left[1+\frac{\mathrm{R}}{100}\right]^{\mathrm{n}}\)
= \(12600\left[1+\frac{10}{100}\right]^{2}\)
= \(12600\left[1+\frac{1}{10}\right]^{2}\)
= \(12600 \times \frac{11}{10} \times \frac{11}{10}\)
= 126 × 121 = 15246
A = ₹ 15246
∴ చక్రవడ్డీ = మొత్తం – అసలు
= 15,246 – 12,600 = ₹ 2646/-

3. ఒక సంవత్సరములో చక్రవడ్డీ లెక్కకట్టు కాలవ్యవధులను, వడ్డీరేటును లెక్కకట్టుము. మను (పేజీ నెం. 115)
1) కొంత మొత్తము 8% వడ్డీ రేటు చొప్పున ప్రతీ 6 నెలలకు చక్రవడ్డీ లెక్కకట్టుచూ 1\(\frac {1}{2}\) సంవత్సరములకు అప్పు తెచ్చెను.
2) కొంత మొత్తమును 4% వడ్డీరేటు చొప్పున ప్రతీ 6 నెలలకు చక్రవడ్డీ లెక్కకట్టుచూ 2 సంవత్సరములకు అప్పుతెచ్చెను.
సాధన.
1) చక్రవడ్డీ 6 నెలలకొకసారి, లెక్కకట్టవలెను. కావున 1\(\frac {1}{2}\) సం॥ కాలంలో 3 కాలవ్యవధులు ఉండును.
∴ n = 3.
కావునా అర్ధసంవత్సర వడ్డీ \(\frac {1}{2}\) × 8% = 4%
∴ n = 3
R = 4%

2) చక్రవడ్డీ 6 నెలలకొకసారి లెక్కకట్టవలెను.
కాబట్టి 2 సం॥లకు 4 కాలవ్యవధులు వచ్చును.
∴ n = 4 అగును.
కావున అర్ధసంవత్సర వడ్డీ \(\frac {1}{2}\) × 4% = 2%
∴ n = 4
R = 2%

ప్రయత్నించండి

1. మీ సైకిల్ గేర్ల నిష్పత్తిని కనుగొనండి. (పేజీ నెం. 96)
పెడల్ వద్ద నున్న పెద్ద పళ్ళచక్రం (chain wheel) పళ్ళను అలాగే వెనక చక్రం వద్ద నున్న చిన్నపళ్ళ చక్రం (sprocket wheel) పళ్ళను లెక్కపెట్టండి. {పెద్ద పళ్ళ చక్రపు పళ్ళ సంఖ్య} : {చిన్నపళ్ళ చక్రపు పళ్ళసంఖ్య}

అప్పుడు పెద్దపళ్ళ చక్రం పళ్ళ సంఖ్య : చిన్న పళ్ళ చక్రం పళ్ళ సంఖ్యను కనుగొనండి. దీనినే మనం గేర్ నిష్పత్తి అంటాం. ఒక్కసారి పెడల్ ను తిప్పడం వలన వెనక ఎన్నిసార్లు తిరిగిందో గమనించి మీ నోట్ పుస్తకంలో రాయండి.
సాధన.
నా సైకిల్ గేర్లలో పెడల్ వద్దనున్న పెద్ద పళ్ళ చక్రానికి అలాగే వెనక చక్రం వద్దనున్న చిన్న పళ్ళచక్రాల మధ్య నిష్పత్తి = 4 : 1 గా ఉన్నది.

2. ఏవైనా ఐదు వివిధ సందర్భాలకు చెందిన శాతములను వార్తాపత్రికల నుండి సేకరించి మీ నోట్ పుస్తకంలో అంటించండి.
సాధన.
‘ద్రవ్యోల్బణం’ మా లోపం :
అంగీకరించిన ప్రధాని మన్మోహన్ : జైపూర్ :
ద్రవ్యోల్బణాన్ని కట్టడి చేయలేకపోవడం యూపీఏ ప్రభుత్వ లోపమని ప్రధాని మన్మోహన్ సింగ్ అంగీకరించారు. ఆదివారం జైపూర్ లో కాంగ్రెస్ మేధోమథన సదస్సులో ఆయన మాట్లాడారు. “మా రికార్డులో ద్రవ్యోల్బణం ఒక, లోపం. యూపీఏ హయాంలో ద్రవ్యోల్బణ సగటు రేటు మేం కోరుకున్న దానికన్నా అధికంగా ఉంది. గత ఎనిమిదేళ్లలో అంతర్జాతీయ మార్కెట్లో పెట్రోలియం ఉత్పత్తుల ధరలు పెరగడం, రైతులకు ఇచ్చే కనీస మద్దతుధరను ప్రభుత్వం పెంచడం ఈ పరిస్థితికి ప్రధాన కారణాలు. ద్రవ్యోల్బణాన్ని నియంత్రించేందుకు ముఖ్యంగా 2013-14లో దీనిని అదుపు చేసేందుకు గట్టి చర్యలు తీసుకోవాల్సిన అవసరముంది” అని తెలిపారు. యూపీఏ పనితీరును ఎ డీఏతో పోల్చి మాట్లాడిన మన్మోహన్.. ఎ డీఏ పాలనలో వృద్ధి రేటు 5.8 శాతంగా ఉండేదని, యూపీఏ హయాంలో అది 8.2 శాతానికి పెరిగిందని పేర్కొన్నారు. 2030 నాటికి మధ్యస్థాయి ఆదాయ దేశాల సరసన భారత్ నిలుస్తుందన్నారు. పేదరిక నిర్మూలన, వ్యవసాయ వృద్ధి పెరుగుదలలోనూ యూపీఏ పనితీరే మెరుగ్గా ఉందని ఆయన తెలిపారు. లోపాలేమైనా ఉంటే నిజాయితీగా ఒప్పుకోవాలని సూచించారు. బలమైన లోక్పాల్ వ్యవస్థ ఏర్పాటుకు ప్రభుత్వం కట్టుబడి ఉందన్నారు.

మళ్ళీ 8 శాతం వృద్ధి రేటును అందుకుంటాం … చిదంబరం :
దేశం తిరిగి ఎనిమిది శాతం వృద్ధి రేటును అందుకుంటుందని కేంద్ర ఆర్థిక మంత్రి పి. చిదంబరం మేధోమథన సదస్సులో విశ్వాసం వ్యక్తంచేశారు. వచ్చే ఆర్థిక సంవత్సరానికి ఆయన ఏడుశాతం వృద్ధి రేటును లక్ష్యంగా పేర్కొన్నారు.

కమొడిటీస్ మార్కెట్ :
వ్యవసాయోత్పత్తులు :
ధనియా ఏప్రిల్ కాంట్రాక్టు గత వారంలో ఎంతో ఆకర్షణీయంగా 10.07 శాతం లాభాన్ని నమోదు చేసింది. గత వారం ముగింపు ధర రూ. 6,954. ఈ కాంట్రాక్టు మీద వచ్చినంత లాభం ఏ ఇతర కాంట్రాక్టు మీద లభించలేదు. ఈ వారంలో దీన్లో కొంత లాభాల స్వీకరణ చోటు చేసుకోవచ్చు. రూ. 7,315 కన్నా పైన ఈ కాంట్రాక్టును విక్రయించడం చక్కని వ్యూహం కాగలదు. రూ. 7,676 కన్నా పైన షార్ట్ పొజిషన్లు తగవు. ఐనా ఏప్రిల్ కాంట్రాక్టు గతవారంలో 12.07 శాతం నష్టపోయి రూ. 3,561 ముగింపు ధరను నమోదు చేసింది. ఈ వారంలో కూడా ఈ కాంట్రాక్టు కొనుగోలు చేయడానికి ఆకర్షణీయంగా కనిపిస్తోంది. యాలుకలు ఫిబ్రవరి కాంట్రాక్టు గతవారంలో 3.21% లాభపడింది. ఈ వారంలో రూ. 1,080 సమీపంలో ఈ కాంట్రాక్టులో లాభాలు స్వీకరించవచ్చు. పసుపు కాంట్రాక్టు గత వారంలో 1.88 శాతం పడిపోయింది. ఈ వారంలోనూ ఇది బలహీనంగా కనిపిస్తోంది. రూ. 6,480 కన్నా కింద ఉంటే ఈ కాంట్రాక్టును విక్రయించవచ్చు. – ఆర్ఎల్‌పీ కమొడిటీ అండ్ డెరివేటివ్స్

20 శాతం సిబ్బంది అంతర్గత బదిలీలు :
ప్రాయోజిత వాణిజ్య బ్యాంకులు తాము అనుసరించే మొబైల్ బ్యాంకింగ్, ఆర్టీజీఎస్, నెఫ్ట్ వంటి ఆధునిక సేవలను గ్రామీణ బ్యాంకులకు అందించాలి. ఇందుకోసం గ్రామీణ బ్యాంకు సిబ్బందిలో యువతను (20% సిబ్బందిని) మెరుగైన అనుభవం కోసం వాణిజ్య బ్యాంకులకు, అక్కడి సిబ్బందిని గ్రామీణ బ్యాంకులకు బదిలీ చేయనున్నారు. ప్రాయోజిత వాణిజ్య బ్యాంకులు తమ సిబ్బందికి నిర్వ హించే శిక్షణ కార్యక్రమాల్లో 10% ఆర్ఆర్ బీ సిబ్బందికి కేటాయించాలి.

బిఎస్ఎన్ఎల్లో లక్షమందికి వీఆర్ఎస్ ! న్యూ ఢిల్లీ :
వేతన భారాన్ని తగ్గించుకోవడానికి స్వచ్ఛంద పదవీ విరమణ పథకం (వీఆర్ఎస్) ద్వారా లక్ష మంది ఉద్యోగులను తగ్గించుకోవాలని భారత్ సంచార్ నిగమ్ (బిఎస్ఎన్ఎల్) యోచిస్తోంది. అవసరానికంటే లక్ష మంది ఉద్యోగులు ఎక్కువగా ఉన్నారని, వీఆర్ఎస్ ద్వారా వీరి భారాన్ని తగ్గించుకోవాలని కంపెనీ భావిస్తున్నట్లు బిఎస్ఎన్ఎల్ ఉన్నతాధికారి ఒకరు తెలిపారు. బిఎస్ఎన్ఎల్ ఆదాయంలో దాదాపు 48 శాతం వేతనాలకే సరిపోతోంది. అదనపు ఉద్యోగులు స్వచ్ఛంద పదవీ విరమణ ద్వారా బయటకు వెళితే … వేతన భారం 10-15 శాతం తగ్గుతుందని అధికారి చెప్పారు. వీఆర్ఎస్ ప్రతిపాదన ప్రభుత్వ పరిశీలనలో ఉందన్నారు. 2011, మార్చి 31 నాటికి బిఎస్ఎన్ఎల్ లో 2.81 లక్షల మంది ఉద్యోగులు పనిచేస్తున్నారు.

3. క్రింది నిష్పత్తుల బహుళ నిష్పత్తిని కనుగొనండి. (పేజీ నెం. 99)
(a) 3 : 4 మరియు 2 : 3
(b) 4 : 5 మరియు 4 : 5
(c) 5 : 7 మరియు 2 : 9
సాధన.
(a) 3 : 4 మరియు 2 : 3ల బహుళ నిష్పత్తి
a : bమరియు c : dల బహుళ నిష్పత్తి = ac : bd
∴ 3 : 4 మరియు 2 : 3ల బహుళ నిష్పత్తి
= (3 × 2) : (3 × 4) = 2 : 4 = 1 : 2
(b) 4 : 5 మరియు 4 : 5ల బహుళ నిష్పత్తి
= (4 × 4) : (5 × 5) = 16 : 25
(c) 5 : 7 మరియు 2 : 9 ల బహుళ నిష్పత్తి
= (5 × 2) : (7 × 9) = 10 : 63

4. నిత్య జీవితంలో బహుళ నిష్పత్తికి కొన్ని ఉదాహరణలు తెల్పుము. (పేజీ నెం. 99)
సాధన.
నిత్యజీవితంలో బహుళ నిష్పత్తికి ఉదాహరణలు
i) 8వ తరగతి విద్యార్థుల (బాలబాలికల) టికెట్ల నిష్పత్తి 3 : 4 మరియు 7వ తరగతి విద్యార్థుల టికెట్ల నిష్పత్తి 4 : 5 లను పోల్చుట.
ii) 4గురు ఒక పనిని 12 రోజులలో పూర్తిచేస్తే 6 గురు అదేపనిని 8 రోజులలో పూర్తిచేయు సందర్భాల మధ్య పోలిక.
iii) కాలం-దూరము – వేగం
(iv) మనుష్యులు-రోజులు-వారి సామర్థ్యాలు మొ॥ వాటిలో బహుళ నిష్పత్తిని ఉపయోగిస్తాం.

5. క్రింది పట్టికలో అమ్మకం ధరలను రాయండి. (పేజీ నెం. 104)

సాధన.

6. (i) ₹ 357.30 లో 20% అంచనావేయండి. (పేజీ నెం. 105)
సాధన.

(ii) ₹ 375.50 లకు 15% అంచనా వేయండి.
సాధన.
375.50 లో 15%

ఆలోచించి, చర్చించి వ్రాయండి

1. ఒక సంఖ్యకు రెండు రెట్లు అనగా ఆ సంఖ్యలో పెరుగుదల 100%. మనం ఆ సంఖ్యలో సగము తీసుకొన్న దానిలో తగ్గుదల శాతము ఎంత ? (పేజీ నెం. 101)
సాధన.
ఒక సంఖ్య రెండు రెట్లు అనగా ఆ సంఖ్యలో పెరుగుదల = \(\frac{(2-1)}{1}\) × 100 = 1 × 100% = 100%
ఒక సంఖ్యలో సగము తీసుకున్న = 1 – \(\frac {1}{2}\) = \(\frac {1}{2}\)
దానిలో తగ్గుదల శాతం = \(\frac{\frac{1}{2}}{1}\) × 100 = 50%

2. ₹ 2400 కన్నా ₹ 2000 అనేది ఎంత శాతం తక్కువ? అలాగే ₹ 2000 కంటే ₹ 2400 ఎంత శాతము ఎక్కువ? ఈ రెండు శాతములు సమానమేనా? (పేజీ నెం. 101)
సాధన.
₹ 2400 కన్నా ₹ 2000 ఎంత తక్కువ శాతం

₹ 2400 కన్నా ₹ 2000 ఎంత తక్కువ శాతం

3. ప్రీతి బట్టలు కొనుటకు ఒక దుకాణమునకు వెళ్ళినది. ఆమె ఎంచుకున్న దుస్తుల ప్రకటన వెల ₹ 2500. దుకాణదారుడు మొదట 5% రుసుము ఇచ్చినాడు మరలా అడుగగా మరొక 3% రుసుము ఇచ్చినాడు. అయిన ఆమెకు లభించిన మొత్తము రుసుము శాతము ఎంత ? అది 8% కి సమానంగా వుంటుందా ? ఆలోచించి మీ మిత్రులతో చర్చించి నోట పుస్తకములో రాయండి. (పేజీ నెం. 105)
సాధన.
ప్రీతి ఎంచుకున్న బట్టల ప్రకటన వెల = ₹ 2500
మొదట 5% రుసుము ఇచ్చిన తరువాత అమ్మకపు వేల = ప్రకటన వెల – రుసుము
= 2500 – \(\frac {5}{100}\) × 2500
= 2500 – 125 = ₹ 2375.
మరలా మరొక 3% రుసుము ఇచ్చిన అమ్మకపు వెల

అదే, 8% రుసుము ఇచ్చిన అమ్మకపు వెల

= 2500 – 200 = 2300
∴ రెండు సందర్భాలలో వచ్చిన అమ్మకపు వెలలు సమానం కావు.
5% పై వచ్చిన రుసుము + 3% పై వచ్చిన రుసుము = 125 + 71.25 = ₹ 196.25
8% పై వచ్చిన రుసుము = ₹200
ఆమెకు లభించిన మొత్తం రుసుము శాతాలు సమానం కావు.

4. అమ్మిన వెల; కొన్నవెల సమానమైతే ఏమి జరుగుతుంది? మన నిత్య జీవితంలో అటువంటి పరిస్థితులు వస్తాయా? పై సందర్భాలలో లాభము లేదా నష్టము కనుగొనుట చాలా తేలిక, కాని వాటిని శాత రూపంలో తెలిపితే మరింత అర్ధవంతంగా ఉంటుంది. లాభము అనేది కొన్న వెలపై పెరుగుదల శాతము మరియు నష్టము అనేది కొన్న వెలపై తగ్గుదల శాతము. (పేజీ నెం. 106)
సాధన.
అమ్మినవెల కొన్నవెలకు సమానమైతే లాభం కానీ, నష్టం కానీ ఉండదు.
ఉదా : నిజజీవితంలో కొన్న వెల, అమ్మిన వెలలు సమానం కావు.
కానీ అలా సమానమైన సందర్భంలో లాభం కాని, నష్టం కాని సంభవించదు.

5. ఒక దుకాణదారుడు రెండు TV లను ఒక్కొక్కటి ₹ 9,900 లకు అమ్మెను. మొదటి దానిపై 10% లాభము, రెండవ దానిపై 10% నష్టము వచ్చిన అతనికి మొత్తము మీద లాభమా ? నష్టమా ? (పేజీ నెం. 108)
సాధన.
ఒక్కొక్క T.V. అమ్మినవెల = ₹ 9,900
రెండు T.V. ల అమ్మకపు వెల మొత్తం = 2 × 9,900
= ₹ 19,800
మొదటి దానిపై 10% లాభం వచ్చిన కొన్నవెల

రెండవ దానిపై 10% నష్టం వచ్చిన కొన్నవెల

∴ రెండు T.V. ల కొన్నవెలల మొత్తం
= 9000 + 11000 = ₹ 20,000
కొన్నవెల > అమ్మినవెల
∴ నష్టం = కొన్నవెల – అమ్మినవెల
= 20000 – 19,800 = 200

∴ నష్టశాతము = 1%

6. ప్రతీ మూడు నెలలకు వడ్డీని లెక్కకట్టిన చక్రవడ్డీ ఎలా మారును ? ఒక సంవత్సరములో ఎన్ని కాలవ్యవధులు వస్తాయి ? మూడు నెలలకు వడ్డీరేటు సంవత్సర వడ్డీ రేటులో ఎంతభాగము ? మీ మిత్రులతో చర్చించండి. (పేజీ నెం. 115)
సాధన.
చక్రవడ్డీ ప్రతి మూడు నెలలకోసారి లెక్కకట్టవలెను.
కావున సంవత్సర వ్యవధిలో 4 కాల వ్యవధులు వస్తాయి.
3 నెలలకు వడ్డీరేటు సంవత్సర వడ్డీరేటులో \(\frac {1}{4}\) వ భాగం అవుతుంది.

SCERT AP 8th Class Maths Solutions Chapter 5 అనుపాతముతో రాశులను పోల్చుట Ex 5.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson అనుపాతముతో రాశులను పోల్చుట Exercise 5.3

ప్రశ్న1.
సుధాకర్ తన ఇంటి మరమ్మత్తుల కొరకు బ్యాంకు నుండి ₹ 15,000 అప్పు తీసుకున్నాడు. అతడు సంవత్సరము నకు 9% వడ్డీరేటు చొప్పున 8 సంవత్సరముల కాలానికి అప్పుతీసుకొనిన, అతడు ప్రతీనెల ఎంత మొత్తము చెల్లించాలి ?
సాధన.
P = 15,000
R = 9%
T = 8 సం॥ = \(\frac {8}{12}\) నెలలు

అతడు నెలనెలా చెల్లించాల్సిన వడ్డీ = ₹ 900

ప్రశ్న2.
ఒక టెలివిజన్ ని ₹ 21,000 లకు కొన్నారు. ఒక సంవత్సరము తరువాత దాని విలువ 5% తగ్గినది (వస్తువుల వాడకము, కాలమును బట్టి వాటి విలువ తగ్గును). ఒక సంవత్సరము తరువాత ఆ టెలివిజన్ విలువ ఎంత?
సాధన.
టెలివిజన్ కొన్న విలువ = ₹ 21,000
ఒక సం॥ తరువాత దాని విలువ = 21000 – 21000 లో 5%

= 21000 – 1050
= ₹ 19,950

ప్రశ్న3.
₹ 8000 లపై 5% వడ్డీ రేటు చొప్పున ప్రతీ సంవత్సరమున కొకసారి వడ్డీ తిరగ కట్టబడిన రెండు సంవత్సరములకు అయ్యే చక్రవడ్డీని, మొత్తమును కనుగొనుము.
సాధన.
P = ₹ 8000; R = 5%
ప్రతి సం॥నకు ఒకసారి చొప్పున వడ్డీ తిరగకట్టిన రెండు సంవత్సరాలకు 2 కాల వ్యవధులు వస్తాయి.
∴ n = 2

∴ మొత్తం (A) = ₹ 8820
చక్రవడ్డీ (C.I.) = మొత్తం – అసలు
= 8820 – 8000 = ₹820

ప్రశ్న4.
₹ 6500 లపై మొదటి సంవత్సరము 5% చొప్పున రెండవ సంవత్సరము 6% వడ్డీ రేటు చొప్పున ప్రతీ సంవత్సరము వడ్డీ తిరిగకట్టబడిన 2 సంవత్సరములకు అయ్యే చక్రవడ్డీని, మొత్తమును కనుగొనుము.
సాధన.
P = ₹ 6500, R = 5%, T = 1 సం॥
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{6500 \times 5 \times 1}{100}\)
= 325
∴ A = P + I = 6500 + 325 = 6825
∴ P = 6825 (రెండవ సంవత్సరం మొదట్లో మొత్తం అసలు అగును)
R = 6%, T = 1 సం॥
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{6825 \times 6 \times 1}{100}\)
∴ A = P + I = 6825 + 409.5
∴ మొత్తము = ₹ 7234.50
చక్రవడ్డీ = ₹ 409.5

ప్రశ్న5.
ప్రతిభ ఒక ఋణ సంస్థ (ఫైనాన్స్ కంపెనీ) నుండి మొదటి కారును కొనడానికి ₹ 47000 లను 17% వడ్డీ రేటుతో 5 సంవత్సరములకు సాధారణ వడ్డీకి అప్పు తీసుకున్నది. అయిన (a) ఆమె ఋణ సంస్థకు ఎంత మొత్తము చెల్లించాలి. (b) ఆ మొత్తాన్ని సమాన వాయిదాలలో చెల్లించాలంటే ఆమె ప్రతీ నెల ఎంత మొత్తము చెల్లించాలి.
సాధన.
P = ₹47000, R = 17%, T = 5 సం॥

∴ చెల్లించాల్సిన మొత్తం (A) = P + I
= 47000 + 39,950 = 86950
a) ఋణసంస్థకు ఆమె చెల్లించాల్సిన మొత్తం = ₹ 86950
b) ఆ మొత్తాన్ని సమాన వాయిదాల్లో చెల్లించాలంటే ఆమె ప్రతినెల చెల్లించాల్సిన మొత్తం

ప్రశ్న6.
2011వ సంవత్సరములో హైదరాబాదు జనాభా 68,09,000 అది ప్రతీ సంవత్సరము 4.7% చొప్పున పెరుగుచున్న 2015వ సంవత్సరము. చివరి నాటికి హైదరాబాదు జనాభా ఎంత అవుతుంది ?
సాధన.
2011 లో హైదరాబాద్ జనాభా = 68,09,000
ప్రతి సం॥ అది 4.7% చొప్పున పెరుగుచున్న 2015 నాటికి హైదరాబాద్ జనాభా
= 6809000 \(\left(1+\frac{4.7}{100}\right)^{4}\)
[∵ P = 6809000, R = 4.7%, n = 4(2015 – 2011)
= 6809000 × \(\frac{104.7}{100} \times \frac{104.7}{100} \times \frac{104.7}{100} \times \frac{104.7}{100}\)
= ₹ 81,82,199

ప్రశ్న7.
₹ 10,000 లను 8\(\frac {1}{2}\)% చొప్పున సంవత్సరమున కొకసారి వడ్డీ తిరిగి లెక్కకట్టు పద్ధతిలో పొదుపుచేసిన 1 సంవత్సరము 3 నెలల కాలంలో వచ్చే చక్రవడ్డీని కనుగొనండి.
సాధన.
P = ₹ 10,000 ; R = 8\(\frac {1}{2}\)% = \(\frac {17}{2}\)%
T = 1 సం॥

= 50 × 17 = 850
∴ I = ₹ 850
∴ A = P + I = 10,000 + 850
A = 10,850
∴ P = 10,850 ; R = 8\(\frac {1}{2}\)% = \(\frac {17}{2}\)%
T(n) = 3 నెలలు = \(\frac {3}{12}\) సం॥ = \(\frac {1}{4}\) సం॥
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{10850 \times \frac{17}{2} \times \frac{1}{4}}{100}\)
= \(\frac{10850 \times 17}{800}\)
I = ₹ 230.5625
∴ అసలు (A) = P + I
= 10850 + 230.5625
= ₹ 11080. 5625

ప్రశ్న8.
ఆరిఫ్ ఒక బ్యాంక్ నుండి ₹ 80,000 లను వడ్డీరేటు 10% చొప్పున అప్పు తీసుకొనెను. (i) సంవత్సరము మరియు (ii) 6 నెలలు తిరిగి వడ్డీ కట్టు కాల వ్యవధులుగా తీసుకొని 1\(\frac {1}{2}\) సంవత్సరములకు వడ్డీ కట్టిన ఆ రెండు మొత్తముల భేదమును కనుగొనుము.
సాధన.
P = ₹ 80,000; R = 10%; T = 1 సం॥
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{80000 \times 10 \times 1}{100}\) = 8000
∴ A = P + I = 80000 + 8000 = ₹ 88,000
మరలా 6 నె॥లకు అగు వడ్డీ :
P = 80000
R= 10%
T = 6 నె॥లు
= \(\frac {1}{2}\) సం॥
I = \(\frac{\text { PTR }}{100}\)
= \(\frac{80000 \times \frac{1}{2} \times 10}{100}\)
= 4000

i) ఒక సంవత్సరం 6 నెలల తరువాత కట్టవలసిన మొత్తం = వడ్డీ + అసలు
= 88000 + 4000
A1 = ₹ 92000

ii) 6 నెలలకొకసారి, చక్రవడ్డీ కట్టవలెనన్న 1\(\frac {1}{2}\) సం॥ చొప్పున 3 కాలవ్యవధులు వస్తాయి.
∴ n = 3 అగును.
R = \(\frac {10}{2}\) = 5%
P = ₹ 80,000

∴ రెండు మొత్తాల మధ్య భేదం = A₂ – A₁ = 92610 – 92000
= ₹ 610

ప్రశ్న9.
నేను ప్రసాద్ వద్ద నుండి ₹ 12000 లను 6% వడ్డీ రేటు చొప్పున సాధారణ వడ్డీకి 2 సంవత్సరముల కాలానికి అప్పు తీసుకున్నాను. నేను అదే మొత్తమును 6% వడ్డీ రేటు చొప్పున సంవత్సరమునకొకసారి తిరిగి వడ్డీ కట్టు పద్ధతిన అప్పు తీసుకున్నచో ఎంతసొమ్ము అదనంగా చెల్లించవలసి వస్తుంది ?
సాధన.
ప్రసాదు వద్ద నుండి తీసుకున్న సొమ్ము = (P)
= ₹ 12000
T = 2 సం॥ R = 6%
∴ I = \(\frac{\text { PTR }}{100}\)
= \(\frac{12000 \times 2 \times 6}{100}\)
I = ₹ 1440
మొత్తం = అసలు + వడ్డీ
A₁ = P + I = 12000 + 1440
= ₹ 13440
∴ 2 సం॥ల తరువాత సాధారణ వడ్డీ రేటు 6% చొప్పున చెల్లించాల్సిన మొత్తం = ₹ 13440
చక్రవడ్డీ చొప్పున 2 సం॥ల తరువాత చెల్లించాల్సిన మొత్తం
P = ₹ 12,000, R = 6%, n = 2 సం॥

∴ చక్రవడ్డీ, సాధారణ వడ్డీల ద్వారా వచ్చు మొత్తాలలో భేదం = 13483.2 – 13440
= ₹ 43.20

ప్రశ్న10.
ఒక ప్రయోగశాలలో, ప్రయోగమును నిర్వహించి బాక్టీరియాలో పెరుగుదల రేటు గంటకు 2.5% అని గుర్తించినారు. ప్రారంభంలో బాక్టీరియా సంఖ్య, 5,06,000 లు వున్నచో రెండు గంటల తరువాత ఆ బాక్టీరియా సంఖ్య ఎంత ?
సాధన.
ప్రారంభంలో ప్రయోగశాలలో గల బాక్టీరియాల సంఖ్య = 5,06,060
గంటకు 2.5 % రేటుతో పెరిగిన, 2 గం॥ల తరువాత ఆ బాక్టీరియాల సంఖ్య
∵ n = 2 గం॥లు

ప్రశ్న11.
కమల బ్యాంకు నుండి స్కూటరు కొనే నిమిత్తం ₹26400 లను 15% వడ్డీ రేటు చొప్పున సంవత్సరమున కొకసారి తిరిగి వడ్డీ కట్టు పద్ధతిలో అప్పు తెచ్చుకున్నది. 2 సంవత్సరముల 4 నెలల తరువాత అప్పు మొత్తము తీర్చివేయవలెనన్న ఆమె చెల్లించవలసిన మొత్తమును కనుగొనుము.
సాధన.
కమల బ్యాంకు నుండి తీసుకున్న మొత్తం = ₹ 26400
వడ్డీ రేటు (R) = 15% చొప్పున 2 సం॥లకు అగు మొత్తం

∴ తదుపరి 4 నెలలకు వడ్డీ కట్టుటకు మొత్తం (₹ 34914) అసలు అగును.
∴ P = 34914, R = 15%, T = 4 నెలలు = \(\frac {4}{22}\) సం॥
= \(\frac {1}{3}\) సం॥
I = \(\frac{\mathrm{PTR}}{100}\) = \(\frac{34914 \times 15 \times \frac{1}{3}}{100}\)
= ₹ 1745.7
∴ 2 సం॥ల 4 నెలల కాలానికి కమల బ్యాంక్ వారికి చెల్లించాల్సిన మొత్తం = 34914 + 1745.7
= ₹ 36659.7

ప్రశ్న12.
భారతి ₹ 12500 లను 12% వడ్డీ రేటు చొప్పున 3 సంవత్సరముల కాలానికి సాధారణ వడ్డీకి అప్పు తీసుకున్నది. మాధురి అదే మొత్తాన్ని అదేకాలానికి 10% వడ్డీ రేటుతో సంవత్సరమునకొకసారి తిరిగి వడ్డీ కట్టు పద్ధతిన అప్పుతెచ్చినది. ఆ ఇద్దరిలో ఎవరు ఎక్కువ వడ్డీని చెల్లించెదరు ? ఎంత ఎక్కువ వడ్డీని చెల్లించెదరు?
సాధన.
భారతి తీసుకున్న అసలు సొమ్ము
P = ₹ 12500
R = 12%
T = 3 సం॥లు
సాధారణ వడ్డీ (I) = \(\frac{\mathrm{PTR}}{100}\)
= \(\frac{12500 \times 12 \times 3}{100}\)
= 125 × 36 = 4500
∴ 3 సం॥ల తరువాత చెల్లించాల్సిన మొత్తం
A₁ = P + I = 12500 + 4500
A₁ = ₹ 17,000
మాధురి చక్రవడ్డీ చొప్పున కట్టాల్సిన మొత్తం

∴ A₁ > A₂
A₁ – A₂ = 17000 – 16637.5
= ₹ 362.5
∴ భారతి, మాధురి కంటే ₹ 362.5 ఎక్కువ వడ్డీ చెల్లించాల్సి ఉంటుంది.

ప్రశ్న13.
₹ 10000 ల విలువ గల యంత్ర సామగ్రిలో తరుగుదల రేటు 5%. అయిన 1 సంవత్సరము తరువాత దాని విలువ ఎంత ?
సాధన.
10,000 విలువ గల యంత్రసామాగ్రి 5% తరుగుదల రేటు ప్రకారం 1 సం॥ తరువాత దాని విలువ

= 95 × 100 = ₹ 9500

ప్రశ్న14.
ఒక పట్టణ ప్రస్తుత జనాభా 12 లక్షలు. సంవత్సరమునకు 4% చొప్పున జనాభా పెరుగుతూ వుంటే 2 సంవత్సరముల తరువాత ఆ పట్టణ జనాభా ఎంత?
సాధన.
పట్టణ ప్రస్తుత జనాభా = 12,00,000
సం॥నకు 4% చొప్పున జనాభా పెరుగుతూ ఉంటే 2 సం॥ల తరువాత ఆ పట్టణ జనాభా

ప్రశ్న15.
₹ 1000 లను 10% వడ్డీరేటు చొప్పున త్రైమాసికంగా తిరిగి వడ్డీ కట్టు పద్ధతిన 1 సంవత్సర కాలానికి అయ్యే చక్రవడ్డీని కనుగొనండి.
సాధన.
₹ 1000 లను 10% వడ్డీ రేటు చొప్పున త్రైమాసికంగా తిరిగి వడ్డీ కట్టిన 1 సం॥కాలానికి అయ్యే మొత్తం
A = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}\)
త్రైమాసికంగా చక్రవడ్డీ కట్టవలెనన్న 1 సం॥నకు 4 కాలవ్యవధులు వస్తాయి.
∴ n = 4, P = 1000, R = \(\frac{10}{4}=\frac{5}{2}\)%
∴ A = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}\)
= \(1000 \times\left(1+\frac{5 / 2}{100}\right)^{4}\)

సం॥ కాలానికి అయ్యే చక్రవడ్డీ = 1103.81 – 1000 = ₹ 103.81

SCERT AP 8th Class Maths Solutions Chapter 5 అనుపాతముతో రాశులను పోల్చుట Ex 5.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson అనుపాతముతో రాశులను పోల్చుట Exercise 5.2

ప్రశ్న1.
2012వ సంవత్సరములో ప్రపంచం మొత్తం మీద అంతర్జాలమును (Internet) ఉపయోగించువారి సంఖ్య 36.4 కోట్లుగా అంచనా వేయడమైనది. వచ్చే 10 సంవత్సరాలలో ఈ సంఖ్య 125% పెరుగునని అంచనా వేయబడినది. అయిన 2022వ సంవత్సరములో అంతర్జాలమును ఉపయోగిస్తారని అంచనా వేయబడిన వారి సంఖ్య ఎంత.?
సాధన.
2012వ సం॥లో ప్రపంచంలో అంతర్జాలాన్ని ఉపయోగించు వారి సంఖ్య = 36.4 కోట్లు.
వచ్చే 10 సం॥లలో ఈ సంఖ్య పెరిగే శాతం = 125%
∴ 2022 లో అంతర్జాలం ఉపయోగించువారి సంఖ్య
= 36.4 కోట్లు + 36.4 కోట్లలో 125%
= 36.4 + \(\frac {125}{100}\) × 36.4
= 36.4 + 45.5
= 81.9 కోట్లు

ప్రశ్న2.
ఒక గృహ యజమాని తన ఇంటి అద్దెను ప్రతీ సంవత్సరము .5% పెంచును. ప్రస్తుతము ఆ ఇంటి అద్దె ₹2500 అయిన రెండు సంవత్సరముల తరువాత ఆ ఇంటి అద్దె ఎంత ?
సాధన.
ప్రస్తుత ఇంటి అద్దె = ₹ 2500
ప్రతి సం॥ 5% ఇంటి అద్దె పెంచుతూ ఉంటే 2 సం॥ల తరువాత ఇంటి అద్దె

ప్రశ్న3.
ఒక కంపెనీ విలువ సోమవారమునాడు ₹ 7.50. మంగళవారము నాడు అది 6% పెరిగి, బుధవారము నాడు 1.5% తగ్గినది. మరల గురువారము నాడు 2% తగ్గిన, శుక్రవారము నాడు ఉదయం ఆ షేర్ విలువ ఎంత ?
సాధన.
శుక్రవారం ఉదయంనాడు ఆ షేర్ విలువ

ప్రశ్న4.
చాలా జిరాక్స్ యంత్రాలలో ప్రతీసారి పరిమాణ శాతమును మార్చడం ద్వారా ఇచ్చిన ప్రతి యొక్క పరిమాణమును పెంచడం లేదా తగ్గించడం చేయవచ్చును. రేష్మా తన వద్ద నున్న 2 సెం.మీ., 4 సెం.మీ. బొమ్మను పరిమాణం పెంచాలని కోరుకున్నది. ఆమె జిరాక్స్ యంత్రములో 150% వేసి దాని ప్రతిని తీసుకున్నది. అయిన ఆమెకు లభించిన ప్రతిలోని బొమ్మ పొడవు, వెడల్పులను కనుగొనుము.
సాధన.
ఇచ్చిన ప్రతి యొక్క పొడవు = 2 సెం.మీ.
వెడల్పు = 4 సెం.మీ.
∴ పొడవు 150% పెరిగిన దాని కొలత
= 2 లో 150%
= \(\frac {150}{100}\) × 2 : 1.5 × 2 = 3 సెం.మీ.
వెడల్పు 150% పెరిగిన దాని కొలత
= 4 లో 150%
= \(\frac {150}{100}\) × 4 = 1.5 × 4 = 6 సెం.మీ.
∴ పొడవు = 3 సెం.మీ; వెడల్పు = 6 సెం.మీ.

ప్రశ్న5.
ఒక పుస్తకము ముద్రిత వెల ₹ 150. దానిపై 15% రుసుము లభించిన ఆ పుస్తకమును కొనుటకు ఎంత మొత్తము చెల్లించవలెను ?
సాధన.
పుస్తకం యొక్క ముద్రిత వెల = ₹ 150
దానిపై లభించిన రుసుము శాతం = 15 %
∴ రుసుము = 150 లో 15%
= \(\frac {15}{100}\) × 150
= ₹ 22.5
∴ ఆ పుస్తకపు కొన్నవెల = 150 – 22.5
= ₹ 127.50

ప్రశ్న6.
ఒక కానుక ప్రకటన వెల₹ 176 దానిని దుకాణదారుడు మీకు ₹ 165 లకు అమ్మిన మీకు లభించిన రుసుమును, రుసుము శాతమును కనుగొనండి.
సాధన.
కానుక ప్రకటనవెల = ₹ 176
అమ్మినవెల = 165
రుసుము = ప్రకటన వెల – అమ్మినవెల
= 176 – 165 = ₹ 11

ప్రశ్న7.
ఒక దుకాణదారుడు ప్రతీ బల్బు ₹ 10 చొప్పున 200 బల్బులను కొనెను. కాని అందులో 5 బల్బులు కాలిపోయి నందున వాటిని బయట పడేసినాడు. మిగిలిన బల్బులను ఒక్కొక్కటి ₹ 12 చొప్పున అమ్మిన మొత్తము మీద అతనికి లాభమా ? నష్టమా ? ఎంత శాతము ?
సాధన.
ప్రతి బల్బు ₹ 10 చొప్పున 200 బల్బుల కొన్నవెల = 200 × 10 = 2000
అందు 5 బల్బులు కాలిపోయిన మిగిలినవి = 200 – 5 = 195
ఒక్కొక్కటి ₹ 12 చొప్పున 195 బల్బుల అమ్మకపు వెల = 195 × 12 = 2340
∴ అమ్మినవెల > కొన్నవెల
∴ లాభం = అమ్మినవెల – కొన్నవెల
= 2340 – 2000 = 340

ప్రశ్న8.
ఈ క్రింది పట్టికలో సరియైన గడులను అవసరమైనచోట మాత్రమే నింపుము.

సాధన.

ప్రశ్న9.
ఒక బల్లను ₹ 2,142,లకు అమ్మగా 5% లాభము వచ్చెను. దానిపై 10% లాభము రావలెనన్న దానిని ఎంతకు అమ్మవలెను ?
సాధన.
ఒక బల్ల అమ్మకపు వెల = ₹ 2142
లాభశాతం = 5%
కొన్నవెల = 100 × \(\frac{2142}{(100+5)}\)
= 100 × \(\frac{2142}{105}\)
= ₹ 2040
షాపువాని వద్ద బల్ల కొన్నవెల మనం మరొక వ్యక్తికి అమ్మేటపుడు అమ్మినవెల అవుతుంది.
∴ అమ్మినవెల = ₹ 2040
లాభశాతం = 10%
అయిన కొన్నవెల = 2040 \(\left(1+\frac{10}{100}\right)\)
= 2040 × \(\frac{110}{100}\)
= ₹ 2244

ప్రశ్న10.
గోపి ఒక గడియారమును 12% లాభమునకు ఇబ్రహీమ్ కు అమ్మెను. ఇబ్రహీమ్ దానిని 5% నష్టమునకు జాను అమ్మెను. జాన్ ఆ గడియారమునకు ₹ 1,330 చెల్లించిన గోపి ఆ గడియారమును ఎంతకు అమ్మెను?
సాధన.
జాన్ గడియారమును కొన్నవెల = ₹ 1330
గోపి ఆ గడియారాన్ని అమ్మినవెల
= 1330 × \(\frac{100}{(100+12)}\) × \(\frac{100}{(100-5)}\)
= 1330 × \(\frac{100}{112}\) × \(\frac{100}{95}\)
∴ గోపి గడియారం కొన్నవెల = ₹ 1250

ప్రశ్న11.
మధు మరియు కవిత ఒక క్రొత్త ఇంటిని ₹3,20,000 లకు కొనిరి. కొన్ని ఆర్థిక ఇబ్బందుల వల్ల ఆ ఇంటిని ₹ 2,80,000 లకు అమ్మిన (a) వారికి వచ్చిన నష్టమును (b) నష్టశాతమును కనుగొనుము.
సాధన.
ఇల్లు కొన్న వెల = ₹ 3,20,000
అమ్మినవెల = ₹ 2,80,000
∴ అమ్మినవెల < కొన్నవెల
a) ∴ నష్టము = కొన్నవెల – అమ్మినవెల
= 3,20,000 – 2,80,000
= 40,000

ప్రశ్న12.
ఒక పాత కార్లను కొని, అమ్ము దుకాణదారుడు ఒక పాత కారును ₹ 1,50,000 లకు కొని దాని మరమ్మత్తులు మరియు రంగు వేయుటకు ₹ 20,000 ఖర్చు చేసెను. అతడు ఆ కారును ₹ 2,00,000 లకు అమ్మిన అతనికి లాభమా ? నష్టమా ? ఎంత శాతము?
సాధన.
పాత కారు కొన్నవెల = అసలు ధర + మరమ్మత్తులు
= 1,50,000 + 20,000
= 1,70,000
ఆ కారు అమ్మినవెల = ₹ 2,00,000
∴ అమ్మినవెల > కొన్నవెల
∴ లాభము = అమ్మినవెల – కొన్నవెల
= 2,00,000 – 1,70,000
లాభం = 30,000

ప్రశ్న13.
లలిత తన పుట్టిన రోజును స్నేహితులతో జరుపుకొనుటకు హోటలు నుండి పార్సెల్ తెప్పించినది. 5% VAT తో కలిపి ₹ 1,450 బిల్లు వేయబడినది. హోటలు వారు బిల్లు మొత్తముపై 8% రుసుము ఇచ్చిన లలిత హోటలు వాడికి కట్టవలసిన మొత్తమును కనుగొనుము.
సాధన.
5% VAT తో వేయబడిన బిల్లు మొత్తం = ₹ 1450
బిల్లుపై 8% రుసుము ఇచ్చిన రుసుము = 1450 లో 8%
= \(\frac{8}{100}\) ×1450 = ₹ 116
∴ రుసుము = ₹ 116
∴ లలిత హోటల్ వారికి కట్టవలసిన మొత్తం (రుసుము పోను) = 1450 – 116
= ₹1334/-

ప్రశ్న14.
క్రింది పట్టికలో VAT తో కలిసిన బిల్లు మొత్తము వ్రాయబడినది. VAT కలపక ముందు ఆ వస్తువుల ధరను కనుగొనుము.

సాధన.

ప్రశ్న15.
ఈ క్రింద ఇచ్చిన వస్తువులకు 8.5% అమ్మకం పన్నుకలుపగా వచ్చిన ధర ఈయబడినది. వాటి కొన్నవెలను కనుగొనుము.
(i) టవలు ₹ 50 (ii) రెండు సబ్బులు ఒక్కొక్కటి ₹ 35
సాధన.
అమ్మకపు పన్ను = 8.5%
(i) టవలు ధర = ₹ 50
అమ్మకపు పన్ను = 50 లో 8.5%
\(\frac{8.5}{100}\) × 50 = ₹ 4.25
∴ కొన్నవెల = అసలు ధర + అమ్మకపు పన్ను
= 50 + 4.25 = 54.25

(ii) రెండు సబ్బులు ఒక్కొక్కటి ₹ 35 చొప్పున వాటి మొత్తం = 2 × 35 = 70
అమ్మకపు పన్ను = 70 లో 8.5%
\(\frac{8.5}{100}\) × 70 = ₹ 5.95
∴ కొన్నవెల = అసలు ధర + అమ్మకపు పన్ను
= 70 + 5.95 = ₹ 75.95

ప్రశ్న16.
ఒక సూపర్ బజారులోని వస్తువు వెలలు 4% అమ్మకపు పన్ను కలిపినను రూపాయలకు సవరింపు అవసరం లేక ‘n’ రూపాయలు అగునట్లు రూపాయలు మరియు పైసలలో నిర్ణయించెను. ‘n’ ధనసంఖ్య అయిన, ‘n’ విలువ కనిష్ఠంగా ఎంత ఉండవచ్చును ?
సాధన.
వస్తువు వెల = ₹ x అనుకొనుము.
వస్తువు వెలపై 4% అమ్మకపు పన్ను విధించగా పెరిగిన వస్తువు వెల
⇒ x + 4% of x = n

∴ n, 26 కు ఒక కనిష్ఠ గుణిజం కావలెను. అపుడు మాత్రమే ‘n’ ను ఖచ్చితంగా పైసలలో కాకుండా రూపాయలలో వ్యక్తం చేయగలం.
∴ n = 13, 26, 39, ….
∴ n = 13 (∵ 13 కనిష్ఠ గుణిజం)

∴ కావలసిన వస్తువు యొక్క వెల
= 12.50 + \(\frac {4}{100}\) × 12.50
= 12.50 + 0.5 = ₹ 13

SCERT AP 8th Class Maths Solutions Chapter 5 అనుపాతముతో రాశులను పోల్చుట Ex 5.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson అనుపాతముతో రాశులను పోల్చుట Exercise 5.1

ప్రశ్న1.
క్రింది వాటికి నిష్పత్తులను కనుగొనుము.
i) స్మిత తన కార్యాలయంలో రోజుకు 6 గంటలు పని చేయును. కాజల్ తన కార్యాలయములో రోజుకు 8 గంటలు పనిచేయును. అయిన వారి పనిగంటల నిష్పత్తిని కనుగొనుము.
ii) ఒక కుండలో 8 లీటర్ల పాలు, మరియొకదానిలో 750 మి.లీ. పాలు ఉన్నాయి. వాటి నిష్పత్తి ఎంత ?
iii) ఒక సైకిలు వేగము గంటకు 15 కి.మీ. ఒక స్కూటర్ -. వేగము గంటకు 30 కి.మీ. వాటి వేగముల నిష్పత్తి ఎంత ?
సాధన.
i) స్మిత మరియు కాజల్ పనిగంటల నిష్పత్తి = 6 : 8
= (2 × 3) : (2 × 4) = 3 : 4

ii) 8 లీటర్లు : 750 మి. లీ.
= 8 × 1000 మి.లీ. : 750 మి.లీ.

iii) సైకిల్, స్కూటర్ వేగాల నిష్పత్తి
= 15 : 30 = (15 × 1) : (15 × 2) = 1 : 2

ప్రశ్న2.
5 : 8 మరియు 3 : 7 ల బహుళ నిష్పత్తి 45 : x అయిన x విలువ ఎంత ?
సాధన.
5 : 8 మరియు 3 : 7 ల బహుళ నిష్పత్తి

ప్రశ్న3.
7 : 5 మరియు 8 : x ల బహుళ నిష్పత్తి 84 : 60 అయిన x విలువ ఎంత ?
సాధన.

ప్రశ్న4.
3 : 4 మరియు 4 : 5 విలోమ నిష్పత్తుల బహుళ నిష్పత్తి 45 : x అయిన x విలువ ఎంత.?
సాధన.
4 : 5 యొక్క విలోమ నిష్పత్తి = 5 : 4
∴ 3 : 4, 5 : 4 ల బహుళ నిష్పత్తి = 45 : x

ప్రశ్న5.
ఒక ప్రాథమిక పాఠశాలలో 60 మంది విద్యార్థులకు ముగ్గురు ఉపాధ్యాయులు ఉండవలెను. ఆ పాఠశాలలో 400 మంది విద్యార్థులు చేరిన ఇదే నిష్పత్తిలో ఎంతమంది ఉపాధ్యాయులు కావలెను ?
సాధన.
60 మంది విద్యార్థులకు ముగ్గురు ఉపాధ్యాయుల చొప్పున 400 మంది విద్యార్థులకు కావలసిన ఉపాధ్యాయుల సంఖ్య
⇒ 60 : 3 = 400 : x ⇒ \(\frac{60}{3}=\frac{400}{x}\)

∴ 400 మంది విద్యార్థులకు కావలసిన ఉపాధ్యాయుల సంఖ్య = 20

ప్రశ్న6.
ఇచ్చిన పటములో ABC ఒక త్రిభుజము, ప్రతీసారి ఒక జత భుజాల కొలతలు తీసుకుంటూ రాయడానికి వీలైన అన్ని నిష్పత్తులను రాయండి.

(సూచన : AB, BC భుజాల నిష్పత్తి = 8 : 6)
సాధన.
ΔABC లో
AB : BC = 8 : 6 = 4 : 38
⇒ BC : AB = 6 : 8 = 3 : 4
BC : CA = 6 : 10 = 3 : 5
⇒ CA : BC = 10 : 6 = 5 : 3
CA : AB = 10 : 8 = 5 : 4
= AB : CA = 8 : 10 = 4 : 5

ప్రశ్న7.
24 మంది విద్యార్థులలో 9 మందికి ఒక పరీక్షలో 75% కంటే తక్కువ మార్కులు వచ్చినవి. 75% కంటే తక్కువ మార్కులు వచ్చిన విద్యార్థుల సంఖ్యకు, 75% కంటే ఎక్కువ మార్కులు వచ్చిన విద్యార్థుల సంఖ్యకు గల నిష్పత్తి ఎంత ?
సాధన.
24 మంది విద్యార్థులలో 75% కంటే తక్కువ మార్కులు వచ్చిన విద్యార్థుల సంఖ్య = 9
75% కంటే ఎక్కువ మార్కులు వచ్చిన విద్యార్థుల సంఖ్య = 24 – 9 = 15
∴ 75 % కంటే తక్కువ మార్కులు వచ్చిన విద్యార్థుల సంఖ్యకు, 75% కంటే ఎక్కువ మార్కులు వచ్చిన విద్యార్థుల సంఖ్యకు గల నిష్పత్తి = 9 : 15
= (3 × 3) : (3 × 5)
= 3 : 5

ప్రశ్న8.
MISSISSIPPI’ అనే పదములోని అచ్చుల సంఖ్యకు, హల్లుల సంఖ్యకు నిష్పత్తి కనుగొని, దానిని కనిష్ఠ పదాలలో తెలపండి.
సాధన.
MISSISSIPPI అనే పదంలో గల హల్లుల సంఖ్య = (MSSSSPP) = 7
అచ్చుల సంఖ్య = (IIII) = 4
∴ పై పదంలో అచ్చుల మరియు హల్లుల సంఖ్యకు గల నిష్పత్తి = 4 : 7

ప్రశ్న9.
రాజేంద్ర, రెహానాలు ఒక వ్యాపారము చేయుచున్నారు. రెహానా ప్రతీనెల వచ్చిన లాభములో 25% తీసుకుంటుంది. ఒక నెలలో రెహానా తీసుకున్న మొత్తం ₹ 2080 అయిన ఆ నెలలో వారికి వచ్చిన మొత్తము లాభమును కనుగొనండి.
సాధన.
మొత్తం లాభం = x అనుకొనిన
x లో 25 % = 2080

⇒ x = 2080 × 4
∴ x = ₹ 8320

ప్రశ్న10.
ΔABCలో AB= 2.2 సెం.మీ., BC= 1.5 సెం.మీ. మరియు AC = 2.3 సెం.మీ. ΔXYZ లో XY = 4.4 సెం.మీ., YZ = 3 సెం.మీ. మరియు XZ = 4.6 సెం.మీ. అయిన AB : XY, BC : YZ, AC : XZ లను కనుగొనండి. ΔABC భుజాల కొలతలు, ΔXYZ భుజాల కొలతలతో అనుపాతంలో ఉన్నాయా?
(సూచన : రెండు త్రిభుజములలో సదృశ భుజాలు ఒకే నిష్పత్తిలో వున్న ఆ త్రిభుజాలు అనుపాతంలో ఉండునని చెప్పవచ్చును)
సాధన.

∴ రెండు త్రిభుజాలలోని భుజాలు ఒకే అనుపాతంలో ఉన్నవి.
∴ ΔABC ~ ΔXYZ

ప్రశ్న11.
మాధురి ఒక సూపర్ మార్కెట్ కు పోగా అక్కడ సరుకుల మారిన ధరలు ఇలా ఉన్నాయి. బియ్యం ధరలో 5% తగ్గుదల, జామ్ మరియు పండ్లపై 8% తగ్గుదల మరియు నూనె, పప్పులపై 10% పెరుగుదల వున్నవి. అయిన ఆ మారిన ధరలు కనుగొనుటకు మాధురికి సహాయము చేయండి.

సాధన.

ప్రశ్న12.
ఒక క్లబ్ లో క్రిందటి సంవత్సరము 2075 మంది చేరినారు. ఈ సంవత్సరము చేరినవారి సంఖ్య 4% తగ్గిన (a) తగ్గినవారి సంఖ్యను (b) ఈ సంవత్సరము చేరిన వారి సంఖ్యను కనుగొనుము.
సాధన.
క్రిందటి సంవత్సరం క్లబ్ లో చేరినవారి సంఖ్య = 2075
ఈ సంవత్సరం చేరినవారి సంఖ్య 4 % తగ్గిన
a) తగ్గినవారి సంఖ్య : 2075 లో 4%

b) ఈ సం॥ చేరిన వారి సంఖ్య
= 2075 – 2075 లో 4%
= 2075 – \(\frac {4}{100}\) × 2075
= 2075 – 83 = 1992

ప్రశ్న13.
ఒక రైతుకు గత సంవత్సరము ప్రత్తి పంటలో 1720 బస్తాల దిగుబడి వచ్చినది. ఈ సంవత్సరములో ఆమె ప్రత్తి. పంటపై దిగుబడి 20% ఎక్కువ వచ్చునని భావించుచున్నది. అయిన ఈ సంవత్సరము ఆమె ఎన్ని బస్తాల దిగుబడిని ఆశిస్తున్నది?
సాధన.
గత సంవత్సరం ప్రత్తి పంటలో వచ్చిన ప్రతి బస్తాల దిగుబడి = 1720
20 % ఎక్కువ దిగుబడి వస్తుందని ఆశించిన రాగల బస్తాల సంఖ్య = 1720 లో 20%
= \(\frac {20}{100}\) × 1720
= 2 × 172
= 344
∴ మొత్తం ఆశించు బస్తాల సంఖ్య = 1720 + 344
= 2064

ప్రశ్న14.
P, Qలు AB రేఖాఖండంపై, \(\overline{\mathrm{AB}}\) కి ఒకే వైపునకు గల బిందువులు. P బిందువు \(\overline{\mathrm{AB}}\) ను 2 : 3 లో, Q బిందువు \(\overline{\mathrm{AB}}\) ను 3 : 4 లో విభజించుచున్నవి. PQ = 2 సెం.మీ. అయిన AB రేఖాఖండపు పొడవును కనుగొనుము.
సాధన.
C అనునది AB మధ్య బిందువు.
P అను బిందువు ABను 2 : 3 నిష్పత్తిలో విభజిస్తుంది.

Q అనునది AB ను 3 : 4 నిష్పత్తిలో విభజిస్తుంది.
PQ = 2 సెం.మీ. (ఇచ్చినది)
PQ = QB – PB = 4 – 3 = 1 భాగం
= 2 సెం.మీ.
∴ AB పొడవు = AQ+ QB (‘Q’ బిందువు దృష్ట్యా )
= 3 + 4 = 7 భాగాలు
AB పొడవు = AP + PB (‘P’ బిందువు దృష్ట్యా)
= 2 + 3 = 5 భాగాలు
∴ 5, 7 భాగాల కనిష్ఠ గుణిజం (అనగా క.సా.గు)
= 5 × 7 = 35
∴ AB పొడవు = 35 భాగాలు
= 35 × 2 = 70 సెం.మీ.