Srinivas

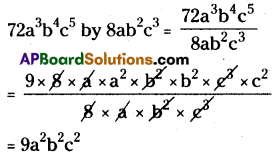
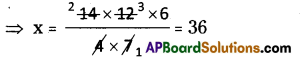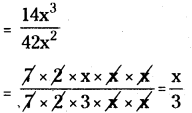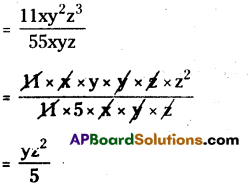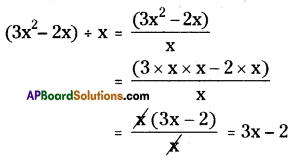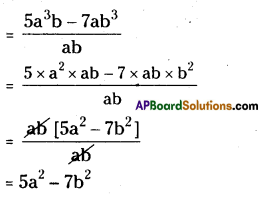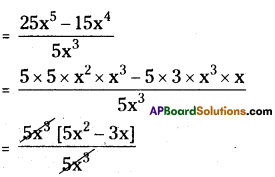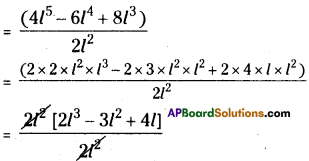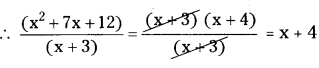AP State Syllabus AP Board 8th Class Maths Solutions Chapter 12 Factorisation Ex 12.4 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson Factorisation Exercise 12.4

Question 1.
Find the errors and correct the following mathematical sentences
(i) 3(x – 9) = 3x – 9
(ii) x(3x+2) = 3x² + 2
(iii) 2x+3x = 5x²
(iv) 2x + x + 3x = sx
(v) 4p + 3p + 2p + p – 9p = 0
(vi) 3x + 2y = 6xy
(vii) (3x)² + 4x +7 = 3x² + 4x +7
(viii) (2x)² + 5x = 4x + 5x = 9x
(ix) (2a + 3)² = 2a² + 6a +9
(x) Substitute x -3 in
(a) x² + 7x + 12 (- 3)² + 7(-3) + 12 = 9 + 4 + 12 = 25
(b) x² – 5x + 6(-3)² – 5(-3) + 69 – 15 + 6 = 0
(c) x² +5x = (-3)² + 5(3) + 6 = -9 – 15 = -24
(xi) (x – 4)² = x² – 16
(xii) (x + 7)² = x² +49
(xiii) (3a + 4b)(a – b)= 3a² – 4a²
(xiv) (x + 4) (x + 2) = x² + 8
(xv) (x – 4) (x – 2) = x²– 8
(xvi) 5x³ ÷ 5 x³ = 0
(xvii) 2x³ + 1 ÷ 2x³ = 1
(xviii) 3x + 2 ÷ 3x = \(\frac{2}{3 x}\)
(xix) 3x + 5 ÷ 3 = 5
(xx) \(\frac{4 x+3}{3}\) = x + 1
Solution:
(i) 3(x – 9) = 3x – 9
3(x – 9) = 3x – 9
⇒ 3x – 3 x 9 = 3x – 9
⇒ 3x – 27 = 3x – 9
⇒ – 27 ≠ – 9
∴ The given sentence is wrong. Correct sentence is 3(x – 9) = 3x – 27.

(ii) x(3x+2) = 3x² + 2
x(3x + 2) = 3x² + 2
⇒ x × 3x + x × 2 = 3x² + 2
⇒ 3x² + 2x ≠ 3x² + 2
∴ The given sentence is wrong.
Correct sentence is x(3x + 2) = 3x² + 2x.

(iii) 2x+3x = 5x²
2x + 3x = 5x²
⇒ 5x = 5x²
⇒ x ≠ x²
∴ The given sentence is wrong. Correct sentence is 2x + 3x = 5x.

(iv) 2x + x + 3x = 5x
2x + x + 3x = 5x
⇒ 6x = 5x
⇒ 6 ≠ 5
∴ The given sentence is wrong. Correct sentence is 2x + 3x = 5x.

(v) 4p + 3p + 2p + p – 9p = 0
4p + 3p + 2p + p – 9p = 0
⇒ 10p – 9p = 0
⇒ p = 0
It is not possible
∴ The given sentence is wrong. Correct sentence is
4p + 3p + 2p + p – 9p – p = 0

(vi) 3x + 2y = 6xy
3x + 2y = 6xy
a + b ≠ ab
∴ The given sentence is wrong.
Correct sentence is 3x x 2y = 6xy.

(vii) (3x)² + 4x +7 = 3x² + 4x +7
(3x)² + 4x +7 = 3x² + 4x +7
⇒ (3x)² = 3x²
⇒ 9x² = 3x²
⇒ 9 = 3
It is not possible
∴ The given sentence is wrong. Correct sentence is
(3x)²+ 4x + 7 = 9x² + 4x + 7.

(viii) (2x)² + 5x = 4x + 5x = 9x
(2x)² + 5x = 4x + 5x = 9x
⇒ 4x² + 5x = 4x + 5x
⇒ 4x² = 4x
⇒ x² = x
⇒ x ≠ √x
∴ The given sentence is wrong. Correct sentence is (2x)² + 5x = 4x² + 5x.

(ix) (2a + 3)² = 2a² + 6a +9
(2a + 3)² = 2a² + 6a +9
⇒ (2a)² + 2 × 2a × 3 + 3² = 2a² + 6a + 9
⇒ 4a² + 12a + 9 = 2a²+ 6a + 9
⇒ 4a² – 2a² = 6a – 12a
⇒ 2a² = – 6a
⇒ 2a ≠ 6
∴ The given sentence is wrong.
Correct sentence is
(2a + 3)² = 4a² + 12a + 9.

(x) Substitute x -3 in
(a) x² + 7x + 12 (- 3)² + 7(-3) + 12 = 9 + 4 + 12 = 25
x² + 7x + 12 = (- 3)² + 7 (- 3) + 12
= 9 – 21 + 12
= 21 – 21
= 0 25 (False)

(b) x² – 5x + 6(-3)² – 5(-3) + 69 – 15 + 6 = 0
x² – 5x + 6 = (-3)² – 5 (- 3) + 6
= 9 + 15 + 6
= 30 ≠ 0 (False)

(c) x² +5x = (-3)² + 5(3) + 6 = -9 – 15 = -24
x² + 5x = (- 3)² + 5 (- 3)
= 9 – 15 = – 6 ≠ 24 (False)

(xi) (x – 4)² = x² – 16
(x – 4)² = x² – 16 = (x)² – (4)²
(a – b)² ≠ a² – b²
∴ (x-4)² ≠ (x)² – (4)²
∴ The given sentence is wrong.
Correct sentence is (x – 4)² = x² – 8x + 16.

(xii) (x + 7)² = x² +49
(x + 7)² = x² + 49 = (x)² + (7)²
(a + b)² ≠ a² + b²
∴ (x+7)² ≠ (x)² – (7)²
∴ The given sentence is wrong.
Correct sentence is (x + 7)² = x² + 14x + 49.

(xiii) (3a + 4b)(a – b)= 3a² – 4a²
3a(a – b) + 4b(a – b) = 3a² – 4²
3a² – 3ab + 4ab – 4b² = – a²
3a² + ab – 4b² ≠ a²
∴ The given sentence is wrong. Correct sentence is
(3a + 4b) (a – b) = 3a² + ab – 4b²

(xiv) (x + 4) (x + 2) = x² + 8
(x + 4) (x + 2) = x² + 8
⇒ x² + 6x + 8 = x² + 8
⇒ 6x ≠ 0
Here ’6x’ term is missing in R.H.S.
∴ The given sentence is wrong. Correct sentence is
(x + 4)(x + 2) = x² + 6x + 8.

(xv) (x – 4) (x – 2) = x²– 8
(x – 4) (x – 2) = x² – 8
⇒ x² – 6x + 8 ≠ x² – 8
∴ The given sentence is wrong. Correct sentence is
(x – 4) (x – 2) = x² – 6x + 8

(xvi) 5x³ ÷ 5 x³ = 0
5x³ ÷ 5 x³ = 0
⇒ x^3-3 = 0
⇒ x⁰ = 0
∴ 1 ≠ 0 (∵ but x° = 1)
∴ The given sentence is wrong. Correct sentence is 5x³ ÷ 5x³ = 1.
In the denominator the term T is missing. .•. The given sentence is wrong. Correct sentence is

(xvii) 2x³ + 1 ÷ 2x³ = 1
2x³ + 1 ÷ 2x³ = 1
⇒ \(\frac{2 x^{3}+1}{2 x^{3}}\) = 1
In the denominator the term T is missing.
∴ The given sentence is wrong. Correct sentence is
2x³ + 1 ÷ 2x³ = 1 + \(\frac{1}{2 \mathrm{x}^{3}}\)

(xviii) 3x + 2 ÷ 3x = \(\frac{2}{3 x}\)
3x + 2 ÷ 3x = \(\frac{2}{3 x}\)
⇒ \(\frac{3 x+2}{3 x}=\frac{2}{3 x}\)
⇒ 1 + \(\frac{2}{3 x}=\frac{2}{3 x}\) ⇒ 1 ≠ 0
∴ The given sentence is wrong. Correct sentence is 3x + 2 ÷ 3x = 1 + \(\frac{2}{3 x}\)

(xix) 3x + 5 ÷ 3 = 5
⇒ \(\frac{3 x+5}{3}\) = 5
⇒ \(\frac{3 x}{3}+\frac{5}{3}\) = 5 ⇒ x + \(\frac{5}{3}\) ≠ 5
∴ It is a wrong sentence.
Correct sentence is 3x + 5 ÷ 3 = x + \(\frac{5}{3}\)

(xx) \(\frac{4 x+3}{3}\) = x + 1
\(\frac{4 x+3}{3}\) = x + 1
⇒ \(\frac{4 \mathrm{x}}{3}+\frac{3}{3}\) = x + 1
⇒ \(\frac{4 \mathrm{x}}{3}\) + 1 ≠ x + 1
∴ It is a wrong sentence.
Correct sentence is \(\frac{4 x+3}{3}=\frac{4 x}{3}+1\)

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions Ex 10.4 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 10th Lesson Direct and Inverse Proportions Exercise 10.4

Question 1.
Rice costing ₹480 is needed for 8 members for 20 days. What is the cost of rice required for 12 members for 15 days?
Solution:
Method – 1: Number of men and rice required to them are in inverse proportion.
Number of men ∝ \(\frac{1}{\text { No. of days }}\)

⇒ Compound ratio of 8:12 and 20: 15
= \(\frac{8}{12}=\frac{20}{15}\) = \(\frac{8}{9}\) …………….. (2)
From (1), (2)
480 : x = 8 : 9
⇒ \(\frac{480}{x}=\frac{8}{9}\)
⇒ x = \(\frac{480 \times 9}{8}\) = ₹540
∴ The cost of required rice is ₹ 540

Method – II :
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
M₁ = No. of men
D₁ = No .of days
W₁ = Cost of rice
∴ M₁ = 8
D₁ = 20
W₁ = ₹ 480
M₂ = 12
D₂ = 15
W₂ = ? (x)

⇒ x = 45 x 12 = ₹ 540
The cost of required rice = ₹ 540/-

Question 2.
10 men can lay a road 75 km. long in 5 days. In how many days can 15 men lay a road 45 km. long?
Solution:
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
∴ M₁ = 10
D₁ = 5
W₁ = 75
M₂ = 15
D₂ = ?
W₂ = 45

∴ x = 2
∴ No. of days are required = 2

Question 3.
24 men working at 8 hours per day can do a piece of work in 15 days. In how many days can 20 men working at 9 hours per day do the same work?
Solution:
M₁D₁H₁ = M₂D₂H₂
∴ M₁ = 24
D₁ = 15 days
H₁ = 8 hrs
M₂ = 20
D₂ = ?
H₂ = 9 hrs
⇒ 24 × 15 × 8 = 20 × x × 9

∴ No. of days are required = 16
[ ∵ No. of men and working hours are in inverse]

Question 4.
175 men can dig a canal 3150 m long in 36 days. How many men are required to dig a canal 3900 m. long in 24 days?
Solution:
\(\frac{M_{1} D_{1}}{W_{1}}=\frac{M_{2} D_{2}}{W_{2}}\)
M₁ = 175
D₁ = 36
W₁ = 3150
M₂ = ?
D₂ = 24
W₂ = 3900

∴ No. of workers are required = 325

Question 5.
If 14 typists typing 6 hours a day can take 12 days to complete the manuscript of a book, then how many days will 4 typists, working 7 hours a day, can take to do the same job?
Solution:
M₁D₁H₁ = M₂D₂H₂
M₁ = 14
D₁ = 12 days
H₁ = 6
M₂ = 4
D₂ = ?
H₂ = 7
⇒ 14 × 12 × 6 = 4 × x × 7

⇒ x = 36
∴ No. of days are required = 36
[ ∵ No of men and working hours are in inverse proportion]

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 12 Factorisation Ex 12.3 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson Factorisation Exercise 12.3

Question 1.
Carry out the following divisions
(i) 48a³ by 6a
(ii) 14x³ by 42x³
(iii) 72a³b⁴c⁵ by 8ab²c³
(iv) 11xy²z³ by 55xyz
(v) -54l⁴m³n² by 9l²m²n²
Solution:
(i) 48a³ by 6a
48a³ ÷ 6a
= \(\frac{6 \times 8 \times a \times a^{2}}{6 \times a}\)
= 8a²

(ii) 14x³ by 42x³
= 14x³ ÷ 42x³

(iii) 72a³b⁴c⁵ by 8ab²c³

(iv) 11xy²z³ by 55xyz
11xy²z³ ÷ 55xyz

(v) -54l⁴m³n² by 9l²m²n²
-54l⁴m³n² ÷ 9l²m²n²

= -6l²m

Question 2.
Divide the given polynomial by the given monomial
(i) (3x² – 2x) ÷ x
(ii) (5a³b – 7ab³) ÷ ab
(iii) (25x⁵ – 15x⁴) ÷ 5x³
(iv) (4l⁵ – 6l⁴ + 8l³) ÷ 2l²
(v) 15 (a³b²c² – a²b³c² + a²b²c³ ) ÷ 3abc
(vi) 3p³– 9p²q – 6pq²) ÷ (-3p)
(vii) (\(\frac{2}{3}\) a² b² c²+ \(\frac{4}{3}\) a b² c³) ÷ \(\frac{1}{2}\)abc
Solution:
(i) (3x² – 2x) ÷ x

(ii) (5a³b – 7ab³) ÷ ab

(iii) (25x⁵ – 15x⁴) ÷ 5x³

= 5x² – 3x (or) x(5x – 3)

(iv) (4l⁵ – 6l⁴ + 8l³) ÷ 2l²

= 2l² – 3l² + 4l = l(2l² – 3l + 4)

(v) 15 (a³ b² c² – a² b³ c² + a² b² c³ ) ÷ 3abc

= 5[a x abc – b x abc + c x abc ]
= 5abc [a – b + c]

(vi) 3p³– 9p²q – 6pq²) ÷ (-3p)

= -[p² – 3pq – 2q²]
= 2² + 3pq – p²

(vii) (\(\frac{2}{3}\) a²b²c²+ \(\frac{4}{3}\) ab²c³) ÷ \(\frac{1}{2}\)abc

Question 3.
Workout the following divisions:
(i) (49x -63) ÷ 7
(ii) 12x (8x – 20,) ÷ 4(2x – 5)
(iii) 11a³ b³ (7c – 35) ÷ 3a² b² (c – 5)
(iv) 54lmn (l + m) (m + n) (n + l) ÷ 8 lmn (l + m) (n +l)
(v) 36(x + 4)(x² + 7x + 10) ÷ 9(x + 4)
(vi) a(a+1)(a+2)(a + 3) ÷ a(a + 3)
Solution:
(i) (49x -63) ÷ 7

(ii) 12x (8x – 20,) ÷ 4(2x – 5)

(iii) 11a³ b³ (7c – 35) ÷ 3a² b² (c – 5)

(iv) 54lmn (l + m) (m + n) (n + l) ÷ 8 lmn (l + m) (n +l)

(v) 36(x + 4)(x² + 7x + 10) ÷ 9(x + 4)

4 ( x² + 7x + 10)
= 4 ( x² + 5x + 2x + 10)
= 4 [x( x + 5) +2(x + 5)]
= 4( x + 5) (x + 2)

(vi) a(a+1)(a+2)(a + 3) ÷ a(a + 3)

= ( a + 1)(a + 2)

Question 4.
Factorize the expressions and divide them as directed:
(i) (x² + 7x + 12) ÷ (x + 3)
(ii) (x² – 8x + 12) ÷ (x – 6)
(iii) (p² + 5p + 4,) (p + l)
(iv) 15ab(a² – 7a + 10) ÷ 3b(a – 2)
(v) 151m (2p² – 2q²) ÷ 3l(p + q)
(vi) 26z³(32z² – 18,) ÷ 13z² (4z – 3)
Solution:
(i) (x² + 7x + 12) ÷ (x + 3)
(x² + 7x + 12) ÷ (x + 3)
x² + 7x + 12 = x² + 3x + 4x + 12
= x(x + 3) + 4(x + 3)
= (x + 3) (x + 4)

(ii) (x² – 8x + 12) ÷ (x – 6)
(x² – 8x + 12) ÷ (x – 6)
x² – 8x + 12 = x² – 6x – 2x + 12
= x(x – 6) – 2(x – 6)
= (x – 6) (x – 2)
∴ (x² – 8x + 12) 4 (x – 6)
= \(\frac{(x-6)(x-2)}{(x-6)}\) = x – 2

(iii) (p² + 5p + 4,) (p + 1)
p² + 5p + 4 = p² + p + 4p + 4
= p(p + 1) + 4(p + 1)
= (p + 1) (p + 4)
(p² + 5p + 4) ÷ (p + 1)
= \(\frac{(p+1)(p+4)}{(p+1)}\) = p + 4

(iv) 15ab(a² – 7a + 10) ÷ 3b(a – 2)
15ab (a² – 7a + 10) ÷ 3b (a – 2)
15ab (a² – 7a + 10) = 15ab (a² – 5a – 2a + 10)
= 15ab [(a² – 2a) – (5a -10)]
= 15ab [a(a – 2) – 5(a – 2)]
= 15ab(a – 2)(a – 5)
∴ 15ab (a² – 7a + 10) ÷ 3b (a – 2)

(v) 151m (2p² – 2q²) ÷ 3l(p + q)
15lm (2p² – 2q²) ÷ 3l (p + q)
15lm (2p² – 2q²) = 15lm x 2(p² – q²)
= 30lm (p + q) (p – q)
∴ 15lm(2p² – 2q²) ÷ 3l(p + q)

(vi) 26z³(32z² – 18,) ÷ 13z² (4z – 3)
26z³(32z² – 18) ÷ 13z² (4z – 3)
26z³(32z² – 18) = 26z³ (2 x 16z² – 2 x 9)
= 26z³ x 2 [16z³ – 9]
= 52z³ [(4z)³ – (3)³]
= 52z³ (4z + 3) (4z – 3)
∴ 26z³ (32z² – 18) ÷ 13z² (4z – 3)

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions Ex 10.3 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 10th Lesson Direct and Inverse Proportions Exercise 10.3

Question 1.
Siri has enough money to buy 5 kg of potatoes at the price of ₹ 8 per kg. How much can she buy for the same amount if the price is increased to ₹ 10 per kg?
Solution:
Number of kgs of potatoes to their price are in inverse proportion.
∴ x₁y₁ = x₂ y₂
⇒ 8 × 5 = 10 × x
⇒ x = \(\frac{8 \times 5}{10}\) = 4 kgs
∴ 4 kgs of potatoes will be purchased at the rate of ₹ 10 per kg.

Question 2.
A camp has food stock for 500 people for 70 days. ¡f200 more people join the camp, how long will the stock last?
Solution:
Number of persons and their food stock are in inverse proportion.
⇒ x₁y₁ = x₂ y₂ (Let y₂ = x say)
⇒ 500 × 70 = (500 + 200) × x
⇒  x = \(\frac{500 \times 70}{700}\) = 5 × 10
∴ x = 50
∴ The food will be stock for (200 + 500) 700 men = 50 days

Question 3.
36 men can do a piece of work in 12 days. ¡n how many days 9 men can do the same work?
Solution:
Number of workers and number of days are in inverse proportion
∴ x₁y₁ = x₂ y₂ let y₂ = x (say)
= 36 × 12 = 9 × x
x = \(\frac{36 \times 12}{9}\) = 48
∴ x = 48 days

Question 4.
A cyclist covers a distance of28 km in 2 hours. Find the time taken by him to cover a distance of 56 km with the same speed.
Solution:
Time and distance are in direct proportion.
∴ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\) , Let y₂ = x (say)
⇒ \(\frac{28}{2}\) = \(\frac{56}{x}\)
⇒ x = \(\frac{56}{14}\)
∴ x = 4 hours

Question 5.
A ship can cover a certain distance in 10 hours at a speed of 16 nautical miles per hour. By how much should its speed be increased so that it takes only 8 hours to cover the same distance? (A nautical mile in a unit of measurement used at sea distance or sea water i.e. 1852 metres).
Solution:
Speed and distance are in inverse proportion.
⇒ x₁y₁ = x₂ y_{2 ,} Let x₂ = x (say)
⇒ 16 × 10 = x × 8
⇒ x = \(\frac{16 \times 10}{8}\)= 20
∴ x = 20
∴ The speed to be increased
= 20 – 16 = 4 nautical miles

Question 6.
5 pumps are required to fill a tank in 1\(\frac { 1 }{ 2 }\) hours. How many pumps of the same type are used to fill the tank in half an hour.
Solution:
Number of pumps and time to fill the tanks are in inverse proportion.
⇒ x₁y₁ = x₂ y₂
⇒ 5 × 1\(\frac { 1 }{ 2 }\) = x x 1\(\frac { 1 }{ 2 }\)
⇒ 5 × \(\frac { 3 }{ 2 }\) = x x \(\frac { 1 }{ 2 }\)
⇒ x = 5 × 3 = 15
∴ Number of pumps required = 15

Question 7.
If 15 workers can build a wall in 48 hours, how many workers will be required to do the same work in 30 hours?
Solution:
Number of workers and time are in inverse proportion.
⇒ x₁y₁ = x₂ y₂
⇒ 15 × 48 = x × 30
⇒ x = \(\frac{15 \times 48}{30}\) = 24
∴ Number of workers required = 24

Question 8.
A School has 8 periods a day each of45 minutes duration. How long would each period become ,if the school has 6 periods a day? ( assuming the number of school hours to be the same)
Solution:
Time and number of periods are in inverse proportion.
⇒ x₁y₁ = x₂ y₂
⇒ 45 × 8 = x × 6
⇒ \(\frac{45 \times 8}{6}\)
⇒ 60 minutes

Question 9.
If z varies directly as xand inversely as y. Find the percentage increase in z due to an increase of 12% in x and a decrease of 20% in y.
Solution:
Given that
z varies directly as x and inversely as y So, z ∝ x (1); z ∝ 1/y ……………… (2)
From (1) & (2), z ∝ \(\frac{\mathrm{x}}{\mathrm{y}}\)

Let x₁ = 100x, x₂ = 112x
(∵ It increases 12%)
y₁ = 100y, y₂ = 80y
(∵ It decreases 20%)
From (3),

∴ z is increased in 40%

Question 10.
If x + 1 men will do the work in x + 1 days, find the number of days that (x + 2) men can finish the same work.
Solution:
Number of workers and number of days are in inverse proportion.
⇒ x₁y₁ = x₂ y₂
⇒ (x + 1) (x + 1) = (x + 2) x k
⇒ k = \(\frac{(x+1)(x+1)}{(x+2)}\)
∴ k = \(\frac{(x+1)^{2}}{(x+2)}\)

Question 11.
Given a rectangle with a fixed perimeter of 24 meters, if we increase the length by 1 m the width and area will vary accordingly. Use the following table of values to look at how the width and area vary as the length varies.
What do you observe? Write your observations in your note books

Solution:

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.5 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.5

Question 1.
Find the missing digits in the following additions.

Solution:
a) 1 + A + 7 = 17 ⇒ A = 17 – 8 = 9
∴ A = 9

b) 2 + 8 + B = 15 ⇒ B = 15 – 10 = 5
2 + 1 + B = 8 ⇒ B = 8 – 3 = 5
∴ B = 5

c) A + 7 + A=13 ⇒ 2A = 6 ⇒ A = 3 A + A + 1 = 7 2A = 6 ⇒ A = 3
∴ A = 3

d) From 1st column
2 + 9 + 9 + A = 26
A = 26 – 20 = 6
From 2nd column
⇒ 2 + 1 + A = 9 ⇒ A = 9 – 3 = 6
∴ A = 6

e) B + 6 + A = 11 or 21
B + A + (1 or 2) = 6
A + 1 = 4 ⇒ A = 3
⇒ From (1), B + 6 + 3 = 11 ⇒ B = 2
∴ A = 3, B = 2

Question 2.
Find the value of A in the following
(a) 7A – 16 = A9 (b) 107 – A9 = lA (e) A36 – 1A4 = 742
Solution:

a) 7A – 16 = A9
A- 6 = 9
If A = 5 it is possible.
∴ A = 5 (or)
7A- 16 = A9
⇒ 7 x 10 + (1 x A) – 16 = (A x 10 + 9 x 1)
⇒ 70 + A – 16 = 10A + 9
⇒ 9A = 45
⇒ A = 5

b) 107 – A9 = 1A
⇒ 107 – (10 x A + 9 x 1) = (1 x 10 + A x 1)
⇒ 107-10A-9= 10 +A
⇒ 11A = 88 A = 8

c) A36 – 1A4 = 742
⇒ (100 x A + 3 x 10 + 6 x 1) – (1 x 100 + A x 10 + 4 x 1) = 742
⇒ 100A + 36 – 100 – 10A – 4 = 742
⇒ 90A = 810
⇒ A = \(\frac{810}{90}\)
∴ A = 9

Question 3.
Find the numerical value of the letters given below-

Solution:
a) If E x 3 = E then E should be equal to 0 (or) 5.
5 x 3 = 15, 0 x 3 = 0
3 x D + 0 = ID [If E = 0]
⇒ 3D = 10 + D
⇒ 2D = 10
⇒ D = 5

∴ F = 1, D = 5, E = 0

b) If H x 6 = H then H should be equal to 0, 2, 6, 8.
G6 = 1G [If H = 0]
⇒ 6G + 0 = 10 + G
⇒ 5G = 10
⇒ G = 10/5 = 2

C = 1, G = 2, H = 0

Question 4.
Replace the letters with appropriate digits
(a) 73K ÷ 8 = 9L
(b) 1MN ÷ 3 = MN
Solution:
a) 73K ÷ 8 = 9L
\(\frac{73 \mathrm{~K}}{8}\) = 9L
If 73K is divisible by 8 then K = {1, 2, 3, …………. 9}
Select K = 6 from the set
∴ \(\frac{73 \mathrm{~K}}{8}\) (R = 0)
∴ \(\frac{73 \mathrm{~K}}{8}\) = 92 = 9L
⇒ 90 + 2 = (9 x 10 + L x 1)
⇒ 90 + 2 = 90 + L
∴ L = 2
∴ K = 6, L = 2

b) 1MN ÷ 3 = MN
If 1MN is divisible by 3 then sum of all the digits is divisible by 3.
⇒ 1 + M + N = 3 x {1,2,3}
Let 1 + M + N = 3 x 2 = 6 say
M + N = 5 …………..(1)
\(\frac{1 \mathrm{MN}}{3}\) = MN
⇒ 1MN = 3[MN]
⇒ 1 x 100 + M x 10 + N x 1
= 3[M x 10 + N x 1]
⇒ 100 + 10M + N = 3[10M + N]
⇒ 100 + 10M + N = 30M + 3N
⇒ 20M + 2N = 100
⇒ 10M + N = 50 …………….. (2)
From (1) & (2)

10 M + N = 50 (-) M + N = 5 9M = 45
∴ M = 5
If M = 5 then
M + N = 5
⇒ N = 0
M = 5, N = 0 [∵ \(\frac{150}{3}\) = 50 ]

Question 5.
If ABB x 999 = ABC 123 (where A, B, C are digits) find the values of A, B, C.
Solution:

From ABB x 999 = ABC 123, the product of units digit is equal to 3.
∴ B x 9 = 3 is the units digit.
If B = 7 then,
7 x 9 = 6 3

∴ A = 8, B = 7, C = 6
∴ The required product = 876123
∴ A = 8, B = 7, C = 6

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 3 Construction of Quadrilaterals Ex 3.3 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson Construction of Quadrilaterals Exercise 3.3

Construct the quadrilateral with the measurements given below :

Question a).
Quadrilateral GOLD: OL = 7.5 cm, GL = 6 cm, LD = 5 cm, DG = 5.5 cm and OD = 10 cm.
(Ex 3.3, Page No. 72)
Solution:
In a quadrilateral GOLD, Rough Diagram
OL = 7.5 cm, GL = 6 cm
LD = 5 cm, DG = 5.5 cm, OD = 10 cm

Construction Steps:

1. Draw a line segment \(\overline{OL}\) equal to radius 7.5 cm.
2. With the centres O, L draw arcs with radius 10 cm and 5 cm respectively. These two arcs meet at point ‘D’.
3. With the centres L, D draw arcs equal to 6 cm and 5.5 cm respectively. These two arcs meet at point ‘G’.
4. Join O, G and L, G. Also join O, D and L, D and G, D.
5. ∴ The required quadrilateral GOLD is formed.

Question b).
Quadrilateral PQRS: PQ = 4.2 cm, QR = 3 cm, PS = 2.8 cm, PR = 4.5 cm and QS = 5 cm.
Solution:


In a quadrilateral PQRS
PQ = 4.2 cm PS = 2.8 cm
QR = 3 cm PR = 4.5 cm
QS = 5 cm

Construction Steps:

1. Draw a line segment \(\overline{P Q}\) with radius 4.2 cm.
2. With the centres P, Q draw arcs equal to the radius 4.5 cm, 3 cm respectively. These two arcs meet at point R’. Join P, R and Q, R.
3. With the centres Q, P draw arcs equal to the radii 5 cm and 2.8 cm respectively. These two arcs meet at point ‘S’.
4. Join P, S and Q, S and S, R.
5. ∴ The required PQRS quadrilateral is formed.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 3 Construction of Quadrilaterals Ex 3.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson Construction of Quadrilaterals Exercise 3.2

Construct quadrilateral with the measurements given below:

Question (a).
Quadrilateral ABCD with AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm andAC= 7cm
Solution:
In Quadrilateral ABCD with AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and AC = 7 cm.

Construction Steps:

1. Draw a line segment \(\overline{\mathrm{AB}}\) with radius 4.5 cms.
2. With the centres A, B draw arcs equal to 7 cm and 5.5 cm respectively. The intersection of these two arcs keep as ‘C’.
3. Join A, C and B, C.
4. With centres C, A draw arcs equal to 4 cm, 6 cm respectively. These intersecting point is keep as ’D’.
   Join D, C and A, D.
5. ∴ The required quadrilateral ABCD is formed.

Question (b).
Quadrilateral PQRS with PQ = 3.5 cm, QR = 4 cm, RS = 5 cm, PS = 4.5 cm and QS= 6.5 cm
Solution:
In a quadrilateral PQRS,
PQ = 3.5 cm, QR = 4 cm, RS = 5 cm,
PS – 4.5 cm, QS = 6.5 cm

Construction Steps:

1. Draw a line segment \(\overline{\mathrm{PQ}}\) with radius 3.5 cm.
2. With the centres P, Q draw arcs equal to 4.5 cm and 6.5 cm respectively.
3. These two arcs meet at point ‘S’.
4. With the centres S, Q draw arcs with radius 5 cm, 4 cm respectively. These two arcs intersected at point ‘R’.
5. Join P, S; Q, S; S, R and Q, R.
6. ∴ The required quadrilateral PQRS is formed.

Question (c).
Parallelogram ABCD with AB = 6cm, CD = 4.5 cm and BD = 7.5 cm
Solution:
In a parallelogram ABCD; AB = 6 cm, BC = 4.5 cm, BD = 7.5 cm
AB = CD (;cm
BC = AD = 4.5 cm
BD = 7.5 cm

Construction Steps:

1. Draw a line segment \(\overline{\mathrm{AB}}\) with radius 6 cms.
2. With the centres A, B draw arcs with radius 4.5 cm, 7.5 cm respectively. These two arcs meet at point ‘D’.
3. With the centres D, B draw arcs with radius 6 cm, 4.5 cm respectively. These two arcs meet at point ‘C’.
4. Join A, D and B, C and D, C and B, D.
5. ∴ The required parallelogram ABCD is formed.

Question (d).
Rhombus NICE with NI = 4 cm and IE = 5.6 cm
Solution:
In a rhombus NI = IC = CE = NE = 4 cm, IE = 5.6 cm

Construction Steps:

1. Draw a line segment \(\overline{\mathrm{NI}}\) with radius 4 cm.
2. With the centres N, I draw two arcs with radius 4 cm, 5.6 cm respectively. These two arcs meet at point E’.
3. With the centres E, I draw arcs with radius 4 cm. These two arcs meet at point ‘C’.
4. Join N, E and I, E. Also join E, C and I, C.
5. .’. The required rhombus NICE is formed.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 3 Construction of Quadrilaterals Ex 3.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson Construction of Quadrilaterals Exercise 3.1

Construct the quadrilaterals with the measurements given below:

Question (a).
Quadrilateral ABCD with AB = 5.5 cm, BC = 3.5 cm, CD = 4 cm, AD = 5 cm and ∠A = 45°.
Solution:
In Quadrilateral ABCD with AB = 5.5 cm, BC = 3.5 cm, CD = 4 cm, AD = 5 cm and ∠A = 45°.

Construction Steps:

1. Construct a line segment \(\overline{\mathrm{AB}}\) with radius 5.5 cm
2. With the centre A draw a ray and an arc which are equL1 to 45° and 5 cm.
3. These intersecting point is keep as ‘D’.
4. With centres D, B draw two arcs equal to radius 4 cm, 3.5 cm respectively.
5. The intersecting point of these two arcs is keep as ‘C’.
6. Join DC and BC. A F
7. ∴ The required quadrilateral ABCD is formed.

Question (b).
Quadrilateral BEST with BE = 2.9 cm, ES = 3.2 cm, ST = 2.7 cm, BT = 3.4 cm and ∠B=75°.
Solution:
In Quadrilateral BEST
BE = 2.9 cm, ES = 3.2 cm, ST = 2.7 cm, BT = 3.4 cm and ∠B=75°.

Construction Steps:

1. Draw a line segment \(\overline{\mathrm{BE}}\) with radius 2.9 cm.
2. With the centre B, draw a ray of 75° and draw 2.9
   an arc with radius 3.4 cm, keep the intersecting point of these two as T.
3. With the centres T, E draw arcs with radius 2.7 cm, 3.2 cm respectively. These intersection point is keep as S’.
4. Join T, S and E,S.
5. ∴ The required quadrilateral BEST is formed.

Question (c).
Parallelogram PQRS with PQ = 4.5 cm, QR =3 cm and ∠PQR = 60°.
Solution:

In a parallelogram PQRS
PQ = 4.5 cm, QR = 3 cm, ZPQR = 60°.
=RS4.5cmzPS=3crn
[: Opposite sides of a I)aralielograrn are equal]

Construction Steps:

1. Draw a line segment ¡i with radius 4.5 cm.
2. With the centre Q draw a ray and an arc equal to 60° and 3 cm.
3. The intersecting point of these two keep as R’.
4. With the centres R, P draw arcs with 4.5 cm, 3 cm respectively. Keep ‘S’ as the intersecting point of these two arcs.
5. Join P, S and R, S.
6. ∴ The required parallelogram PQRS is formed.

Question (d).
Rhombus MATH with AT =4 cm, ∠MAT =120°.
Solution:

Construction Steps:

1. Draw a line segment \(\overline{\mathrm{MA}}\) with radius 4 cm.
2. With the centre A draw a ray and an arc equal to 120°, 4 cm. These two intersecting point be keep as T.
3. With the centres M, T draw arcs equal to 4 cms.
   These two arcs intersected at the point ‘H’.
4. Join M, H and T, H.
5. ∴ The required rhombus MATH is formed.

Question (e).
Rectangle FLAT with FL =5 cm, LA= 3 cm.
Solution:


In a rectangle FLAT
FL=AT=5cm, LA = TF = 3cm, ∠F = ∠L = ∠A = ∠T = 90°

Construction Steps:

1. Draw a line segment \(\overline{\mathrm{FL}}\) with radius 5 cm.
2. With the centre F draw a ray and an arc equal to 900, 3 cm.
   These to meet at point T.
3. With the centres T, L draw arcs equal to 5 cm, 3 cm respectively.
4. These two arcs meet at the point ‘A’.
5. Join T, A and L, A.
6. ∴ The required rectangle FLAT is formed.

Question (f).
Square LUDO with LU = 4.5 cm.
Solution:


In a square LUDO
LU = UD = DO = OL = 4.5 cm
∠L = ∠U = ∠D = ∠O = 90°

Construction Steps: 45

1. Draw a line segment \(\overline{\mathrm{LU}}\) with radius 4.5 cm.
2. With the centre ‘L’, draw a ray of 90° and an arc with radius 4.5 cm. These two meet at the point ‘O’.
3. Now with the centre U’, draw another ray of 90° and an arc with radius 4.5 cm. These two meet at the point “D”.
4. Join O, D.
5. ∴ The required square LUDO is formed.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 5 Comparing Quantities Using Proportion Ex 5.3 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson Comparing Quantities Using Proportion Exercise 5.3

Question 1.
Sudhakar borrows ₹ 15000 from a bank to renovate his house. He borrows the money at 9% p.a. simple interest over 8 years. What are his monthly repayments’?
Solution:
P = 15,000
R = 9%
T = 8 years

A = ₹ 25800
∴ His monthly payment = \(\frac{25800}{8 \times 12}\)
= ₹268.75
∴ Monthly he has to pay = ₹268.75

Question 2.
A TV was bought at a price of ₹ 21000. After 1 year the value of the TV was depreciated by 5% (Depreciation means reduction of the value due to use and age of the item). Find the value of the TV after 1 year.
Solution:
The C.P. of T.V = ₹ 21,000.
After 1 year its value
= 21000 – 5% of 21000
=21000 – \(\frac { 5 }{ 100 }\) × 21000
= 21000 – 1050
= ₹19,950

Question 3.
Find the amount and the compound interest on ₹ 8000 at 5% per annum, for 2 years
compounded annually.
Solution:
P = ₹8000
R = 5%
The interest is compounded every year.
Then 2 time periods wII be occurred.
∴ n = 2

∴ Amount (A) = ₹8820
C.I = A – P
= 8820 – 8000 = ₹ 820

Question 4.
Find the amount and the compound interest on ₹ 6500 for 2 years, compounded annually, the rate of interest being 5% per annum during the first year and 6% per annum during the second year.
Solution:
P = ₹ 6500
R = 5%
T = 1 years
∴ \(\frac{\mathrm{PTR}}{100}=\frac{6500 \times 5 \times 1}{100}\) = 325
∴ A = P + I = 6500 + 325 = 6825
∴ P = 6825
(At the begining of 2,id year A=P)
R = 6%
T = 1 year
∴ \(\frac{\mathrm{PTR}}{100}=\frac{6825 \times 6 \times 1}{100}\) = 409.5
∴ A = P + I = 6825 + 409.5
∴ Amount = ₹ 7234.50
C.I. = A – P
= ₹ 7234.50 – 6500
= ₹734.50

Question 5.
Prathibha borrows ₹47000 from a fmance company to buy her first car. The rate of simple interest is 17% and she borrows the money over a 5 year period. Find: (a) How much
amount Prathibha should repay the finance company at the end of five years. (b) her equal
monthly repayments.
Solution:
P = ₹ 47000
R = 17%
T =5 years
∴ I = \(\frac{\mathrm{PTR}}{100}=\frac{47000 \times 5 \times 17}{100}\)
= ₹ 39,950

a) Amount to be paid
A = P + I
= 47000 + 39,950
= 86950
∴ Amount to be pay = ₹ 86950

b) In monthly equal instalments she has to pay

= 149.1
= ₹ 1450 (approx)

Question 6.
The population of Hyderabad was 68,09,000 in the year 2011. If it increases at the rate of 4.7% per annum. What will be the population at the end of the year 2015.
Solution:
The population of Hyderabad
= 68,09,000
If every year increase in 4.7%.
Then the population of the city in 2015
= 68,09,000 ( 1 + \(\frac{4.7}{100}\) )⁴
100 J
[ ∵ P = 6809000, R = 4.7 %, n = 4(2015 -2011)]
= 68,09,000 x \(\frac{104.7}{100} \times \frac{104.7}{100} \times \frac{104.7}{100} \times \frac{104.7}{100}\)
= 81,82,199

Question 7.
Find Compound interest paid when a sum of ₹ 10000 is invested for 1 year and 3 months at 8\(\frac{1}{2}\) % per annum compounded annually.
Solution:
P = ₹10,000; R = 8\(\frac { 1 }{ 2 }\) % = \(\frac { 17 }{ 2 }\)%
T = 1 year

= 50 × 17 = 850
∴ I = ₹ 850
∴ A = P + I = 10,000 + 850
A = 10,850
∴ P = 10,850; R = \(\frac { 17 }{ 2 }\)% % ; T = 3 months

= ₹ 230.50
∴ Compound Interest
= 850 + 230.50
= ₹ 1080.50

Question 8.
Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the
difference in amounts he would be paying after 1\(\frac{1}{2}\) years, if the interest is (i) compounded annually (ii) compounded half yearly.
Solution:
P = ₹ 80,000; R = 10%;
T = 1 year
∴ \(\frac{\mathrm{PTR}}{100}\) = \(\frac{80000 \times 10 \times 1}{100}\)
= ₹8000
∴ A = P + I = 80000 + 8000
= ₹ 88,000

Interest on 6 months :
P = 88,000 ; R = 10% ; T = 6 Months
= \(\frac { 1 }{ 2 }\) year

i) The amount to be paid after 1 year 6 months = P + I
= 88000 + 4400
A₁ = ₹ 92,400

ii) He has to pay compounded on
every 6 months in 1 \(\frac { 1 }{ 2 }\) years
∴ 3 time periods will be occurred.
∴ n = 3
R = \(\frac { 10 }{ 2 }\) = 5% P = ₹ 80,000


A₂ = ₹ 92610
∴ Difference between the amounts = A₂ – A₁ = 92610 – 92400 = ₹ 210

Question 9.
I borrowed ₹ 12000 from Prasad at 6°/o per annum simple interest for 2 years. Had
I borrowed this sum at 6% per annum compounded annually, what extra amount would
I have to pay9
Solution:
Sum borrowed from Prasad
P = ₹ 12000
T = 2 years;
R = 6%

= ₹144O
A = P + I
A₁ = P + I = 12000 + 1440
= ₹13440
12000 + 1440 , = ₹ 13440
∴ He has to pay the amount after 2 years at the rate of 6% on C.I.
P = ₹12,000; R = 6%; n = 2 years

A₂ = ₹13483.2
∴ The difference between the C.I and S.I = 13483.2 – 13440
= ₹ 43.20

Question 10.
In a laboratory the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000
Solution:
No. of bacteria in a laboratory = 5,06,000
If they are increased at the rate of 2.5% per hour then their number after 2 hours

Question 11.
Kamala borrowed ₹ 26400 from a bank to buy a scooter at a rate of 15% per annum compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
Solution:
Kanala borrowed from bank = ₹ 26400
Rah of interest (R) =15%
n = 2 years

After 4 rpnths the amount will be ₹ 34914
∴ P = 34914; R = 15%; T = 4 months
T = \(\frac { 4 }{ 12 }\) year
= \(\frac { 1 }{ 3 }\) year
∴ \(I=\frac{P T R}{100}=\frac{34914 \times 15 \times \frac{1}{3}}{100}\)
= ₹1745.7
∴ Kamala has to pay the amount after 2 years and 4 months to the bank = 34914 + 1745.7
= ₹36659.7

Question 12.
Bharathi borrows an amount of ₹ 12500 at 12% per annum for3 years at a simple interest and Madhuri borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
Bharathi borrowed the sum
P = ₹12500
R = 12%
T = 3 years
S. I (I) = \(\frac { PTR }{ 100 }\)
= \(\frac{12500 \times 12 \times 3}{100}\)
= 125 × 36
= 4500
After 3 years she has to pay
(A₁)= P + I
= 12500 + 4500 .
A₁ = ₹17,000
Madhuri has to pay the amount on


A₂ = 16637.5
∴ A₁ > A₂
A₁ – A₂ = 17000 – 16637.5
= ₹ 362.5
∴ Bharathi has to pay ₹ 362.5 more than Madhuri.

Question 13.
Machinery worth ₹ 10000 depreciated by 5%. Find its value after 1 year.
Solution:
The value of machinery after 1 year on 5% depreciation

= 95 × 100
= ₹ 9500

Question 14.
Find the population of a city after 2 years which is at present 12 lakh, if the rate of increase is 4%.
Solution:
Present population of a city = 12,00,000 If its population increases at the rate of 4%, then the population after 2 years

= 120 × 104 × 104
= 12,97,920

Question 15.
Calculate compound interest on ₹ 1000 over a period of 1 year at 10% per annum, if interest is compounded quarterly?
Solution:
compounded quarterly then 4 time periods will be there in 1 year.
∴ n = 4
C.I. on ₹ 1000 over a period of 1 year at
10% per annum A = P (1 + \(\frac{\mathrm{R}}{100}\) )ⁿ
P = 1000; n = 4; R = \(\frac{10}{4}=\frac{5}{2}\) %

= ₹ 1103.81
A = ₹ 1103.81
C.I. for 1 year
= 1103.81 – 1000
= ₹ 10.81

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 7 Frequency Distribution Tables and Graphs Ex 7.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 7th Lesson Frequency Distribution Tables and Graphs Exercise 7.2

Question 1.
Given below are the ages of 45 people in a colony.
Construct grouped frequency distribution for the given data with 6 class intervals.

Solution:
Number of classes = 6
Range = Maximum value – Minimum value = 63 – 5 = 58

Question 2.
Number of students in 30 class rooms in a school are given below. Construct a frequency
distribution table for the data with a exclusive class interval of 4 (students).

Solution:
Class Interval (C.I.) = 4
Range = Maximum value – Minimum value = 40 – 15 = 25
No. of classes = \(\frac{\text { Range }}{\mathrm{C} . \mathrm{I}}=\frac{25}{4}\) = 6.25 *(approx ‘6’)

Question 3.
Class intervals in a grouped frequency distribution are given as 4 – 11, 12 – 19, 20 – 27, 28 – 35, 36 – 43. Write the next two class intervals. (1) What is the length of each class
interval? (ii) Write the class boundaries of all classes, (iii) What are the class marks of
each class?
Solution:
The given class intervals are 4-11,12 -19, 20 – 27, 28 – 35, 36 – 43
The next two class intervals are 44 – 51, 52 – 59
i) The length of each class interval is 8
ii) Boundaries of classes :
iii) Class = \(\frac{3.5+11.5}{2}=\frac{15}{2}\) = 7.5

Question 4.
In the following grouped frequency distribution table class marks are given.

(i) Construct class intervals of the data. (Exclusive class intervals)
(ii) Construct less than cumulative frequencies and
(iii) Construct greater than cumulative frequencies.
Solution:

To determine the lower boundary of first class :
The difference between two marks of consecutive classes = h = 22-10 = 12
Let the marks of each class be ‘x’ then the boundaries of the classes be
Lower boundary of first class = x – \(\frac{\mathrm{h}}{2}\) = 10 – \(\frac{12}{2}\) = 10 – 6 = 4
Upper boundary = 10 + \(\frac{12}{2}\) = 10 + 6 = 16
We can determine the remaining classes in the same way.

Question 5.
The marks obtained by 35 students in a test in statistics (out of 50) are as below.

Construct a frequency distribution table with equal class intervals, one of them being 10-20(20 is not included).
Solution:
The frequency distribution table is

C.I. = 10 (from 10 – 20)
Range = 48 – 1 = 47
No. of classes = = 4.7 = 5 (approx)

Question 6.
Construct the class boundaries of the following frequency distribution table. Also construct less than cumulative and greater than cumulative frequency tables.

Solution:

Question 7.
Cumulative frequency table is given below. Which type of cumulative frequency is given. Try to build the frequencies of respective class intervals.

Solution:
In the given table frequencies are increasing from top to bottom. So, it is less than cumulative frequency distribution

∴ Thee required less than C.F. distribution table is

Question 8.
Number of readers in a library are given below. Write the frequency of respective classes.
Also write the less than cumulative fequency table.

Solution:

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 5 Comparing Quantities Using Proportion Ex 5.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 5th Lesson Comparing Quantities Using Proportion Exercise 5.2

Question 1.
In the year 2012, it was estimated that there were 36.4 crore Internet users worldwide. In
the next ten years, that number will be increased by 125%. Estimate the number of Internet
users worldwide in 2022.
Solution:
Internet users in the year 2012
= 36.4 crores.
The number will be increased by next
10 years = 125%
∴ The no. of internet users in the year 2022
= 36.4 + 125% of 36.4
= 36.4 + \(\frac { 125 }{ 100 }\) × 36.4
= 36.4 + 45.5
= 81.9 crores.

Question 2.
A owner increases the rent of his house by 5% at the end of each year. If currently its rent is ₹ 2500 per month, how much will be the rent after 2 years’?
Solution:
Present house rent = ₹ 2500 If the owner increases the rent by 5% on every year then the rent of the house after 2 years

= 2500 × \(\frac { 21 }{ 20 }\) x \(\frac { 21 }{ 20 }\)
= ₹ 2756.25

Question 3.
On Monday, the value of a company’s shares was ₹ 7.50. The price increased by 6% on Tuesday, decreased by 1.5% on Wednesday, and decreased by 2% on Thursday. Find the value of each share when trade opened on Friday.
Solution:
The value of the share when trade opened on Friday
= ₹ 7.674

Question 4.
With most of the Xerox machines. you can reduce or enlarge your original by entering a percentage for the copy. Reshma wanted to enlarge a 2 cm by 4 cm drawing. She set the Xerox machine for 150% and copied her drawing. What will be the dimensions of the
copy of the drawing be’?
Solution:
Length of the copy = 2 cm
breadth = 4 cm
If the length is increase in 150% then its
measure = 150 % of 2 cm
= \(\frac { 150 }{ 100 }\) × 2 = 1.5 × 2 = 3 cm

If the breadth is increase in 150% then
its measure = 150 % of 4 cm 150
= \(\frac { 150 }{ 100 }\) × 4 = 1.5 × 4 = 6 cm
100
∴ New length = 3 cm
breadth = 6 cm

Question 5.
The printed price of a book is ₹ 150. And discount is 15%. Find the actual amount to be paid.
Solution:
The printed price of a book = ₹ 150
Discount % = 15%
∴ Discount = 15% of 150
= \(\frac { 15 }{ 100 }\) × 150 = ₹22.5
∴ The C.P. of a book = 150 – 22.5
= ₹127.50/-

Question 6.
The marked price of an gift item is ₹ 176 and sold it for ₹ 165. Find the discount percent.
Solution:
Marked price of a gift = ₹176
S.P. = 165
Discount = 176 – 165 = ₹ 11

Question 7.
A shop keeper purchased 200 bulbs for ₹10 each. However 5 bulbs were fused and put
them into scrap. The remaining were sold at ₹12 each. Find the gain or loss percent.
Solution:
The C.P. of 200 bulbs at the rate of ₹10 for each = 200 × 10 = ₹ 2000
If 5 bulbs are fused then remaining are
= 200 – 5 = 195
∴ TheS.P. of 195 bulbs at the rate of ₹12 for each = 195 × 12 = ₹ 2340
∴ S.P. > C.P.
∴ Profit = S.P.-C.P.
= 2340 – 2000 = 340
Profit = \(\frac { Profit }{ C.P }\) × 100 = \(\frac { 340 }{ 2000 }\) × 100
Profit = 17%

Question 8.
Complete the following table with appropriate entries (Wherever possible)

Solution:

Question 9.
A table was sold for ₹2,142 at a gain of 5%. At what price should it be sold to gain 10%.
Solution:
S.P. of a table = ₹ 2142
Profit = 5%

∴ The C.P. of buyyer = ₹ 2040
Profit % = 10%

∴ S.P. = ₹2244

Question 10.
Gopi sold a watch to Ibrahim at 12% gain and Ibrahim sold it to John at a loss of 5%. If John paid ₹1,330, then find how much did Gopi sold it?
Solution:
. Let Gopi’s cost price = ₹100
Gain = 12%
∴ Gopi’s selling price to Ibrahim or Ibrahim’s cost price = ₹100 + ₹12 = ₹112
∴ Ibrahim’s loss = 5%
∴ Ibrahim’s selling price =
\(112\left(\frac{100-5}{100}\right)=\frac{112 \times 95}{100}\) = ₹106.40
For ₹100 we get = ₹106.40
For ₹1330 how much we get ?

Question 11.
Madhu and Kavitha purchased a new house for ₹3,20,000. Due to some economic
problems they sold the house for ₹2,80,000. Find (a) The loss incurred (b) the loss percentage.
Solution:
C.P. of a house = ₹ 3,20,000
S.P. of a house = ₹ 2,80,000
∴ C.P. > S.P.
a) Loss
= C.P. – S.P.
= 3,20,000 – 2,80,000 = 40,000

Question 12.
A pre-owned car show-room owner bought a second hand car for ₹ 1,50,000. He spent ₹20,000 on repairs and painting, then sold it for ₹ 2,00,000. Find whether he gets profit or loss. If so, what percent?
Solution:
After repair, the C.P of a car
= 1,50,000 + 20,000 = 1,70,000
S.P. of a ear = ₹ 2,00,000
∴ S.P. > C.P.
∴ Profit = S.P.-C.P.
= 2,00,000-1,70,000= 30,000
Profit = \(\frac { Profit }{ C.P }\) × 100
\(\frac { 30,000 }{ 1,70,000 }\) × 100 = Profit = \(\frac { 300 }{ 17 }\)
Profit% = 17.64%

Question 13.
Lalitha took a parcel from a hotel to celebrate her birthday with her friends. It was billed with ₹ 1,450 including 5% VAT. Lalitha asked for some discount, the hotel owner gave 8% discount on the bill amount. Now find the actual amount that lalitha has to pay to the hotel owner
Solution:
After allowing 5% VAT, the total bill = ₹ 1450
If 8% discount is allowed on bill, then
Discount = 8% of 1450
\(\frac { 8 }{ 100}\) × 1450 = ₹116
Discount = ₹116
∴ Lalitha has to pay the bill = 1450 -116
= ₹ 1334

Question 14.
If VAT is included in the price, find the original price of each of the following.

Solution:

Question 15.
Find the buying price of each of the following items when a sales tax of 5% is added on them.
(1) a towel of ₹50 (ii) Two bars of soap at ₹35 each.
Solution:
Given that Sales tax = 5%
(i) Cost of a towel = ₹ 50
Sales Tax = 5% of 50
= \(\frac { 5 }{ 100 }\) x 50 = \(\frac { 5 }{ 2 }\) = ₹ 2.50
∴ C.P. = Net Price + Sales
Tax = 50 + 2.50 = ₹ 52.50

(ii) The cost of two soaps at the rate of
₹ 35 each = 2 × 35 = ₹ 70
Sales Tax = 5% of 70
= \(\frac { 5 }{ 100 }\) × 70 = \(\frac { 7 }{ 2 }\) = ₹ 3.50
∴ C.P. = Net Price + Sales
Tax = 70 + 3.50 = ₹ 73.50

Question 16.
A Super-Bazar prices an item in rupees and paise so that when 4% sales tax is added, no rounding is necessary because the result is exactly in ‘n’ rupees, where ‘n’ is a positive integer. Find the smallest value of ’n’.
Solution:
Let the cost price = x say
∴ If x is increased 4% sales tax is added then
x + 4% of x = n
x + \(\frac { 4 }{ 100 }\) × x = n
\(\frac { 140x }{ 100 }\) = n
x = x = n × \(\frac { 100 }{ 104 }\) = \(\frac{25 \times \mathrm{n}}{26}\)
∴ n should be a least multiple of 26, then only the value of the article should be represented in only rupees.

[∵n = 13, 26, 39. from them 13 should betaken]
:. Required value of the article
=12.50 + \(\frac { 4 }{ 100 }\) × 12.5
12.50 + 0.5 = ₹13

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.5 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 6th Lesson Square Roots and Cube Roots Exercise 6.5

Question 1.
Find the cube root of the following numbers by prime factorization method.
(i) 343
(ii) 729
(iii) 1331
(iv) 2744
Solution:

Question 2.
Find the cube root of the following numbers through estimation’?
(i) 512
(ii) 2197
(iii) 3375
(iv) 5832
Solution:
Step 1: Start making groups of three digits starting from the unit place.
i.e, \(\overline{512}\) First group is 512

Step 2: First group i.e 512 will give us the units digit of the cube root. As 512 ends with 2, then its cube root ends with 8 (2 x 2 x 2) So the units place of the cube root will be 8.

Step 3: Now take the second group i.e. 0. Which is 0³ < 1 < 2³.
So the least number is ‘0′.
∴ Tens digit of a cube root of a number be 0.
∴ \(\sqrt[3]{512}\) = 08 = 8

(ii) 2197
Step 1: Start making groups of three digits starting from the unit place.

Step 2: First group i.e., 197 will give us the units digit of the cube root.
As 197 ends with 7, its cube root ends with 3. ‘
[∵ 3 x 3 x 3 = 27]
∴ Its units digit is 7.

Step 3: Now take the second group i.e.,2
We know that i3 < 2 < 2
∴ The least number be 1.
∴ The required number is 13.
∴ \(\sqrt[3]{2197}=\sqrt[3]{13 \times 13 \times 13}=\sqrt[\not]]{(13)^{8}}\)
= 13

(iii) 3375
Step 1: Start making groups of three digits starting from the unit place.
i.e.;

Step 2: First group is 375. Its units digit is 5.
∴ The cube root is also ends with 5.
∴ The units place of the cube root will be 5.

Step 3: Now take the second group,
i.e., 3 we know that 1³ < 3³ <2³
∴ The least number is 1.
∴ The tens digit of a cube root will be 1.
∴ The required number = 15
\(\sqrt[3]{3375}=\sqrt[3]{15 \times 15 \times 15}=\sqrt[\not]{15^{\not 3}}=15\)

(iv) 5832
Step 1: Start making groups of three digits starting from the unit place.

Step 2: The units digit of 832 is 2.
∴ The cube root of the number ends with units digit 8.
[∵ 8 x 8 x 8 = 512]

Step 3: In the second group i.e., 5 lie between 1 and 6
i.e., 1³ < 5 < 2³
∴ The tens digit of a number will bel.
∴ The required number is 18.
∴ \(\sqrt[3]{5832}=\sqrt[3]{18 \times 18 \times 18}=\sqrt[3]{(18)^{3}}\)
= 18

Question 3.
State true or false?
(i) Cube of an even number is an odd number
(ii) A perfect cube may end with two zeros
(iii) If a number ends with 5, then its cube ends with 5
(iv) Cube of a number ending with zero has three zeros at its right
(v) The cube of a single digit number may be a single digit number.
(vi) There is no perfect cube which ends with 8
(vii) The cube of a two digit number may be a three digit number.
Solution:
(i) Cube of an even number is an odd number (F)
(ii) A perfect cube may end with two zeros (F)
(iii) If a number ends with 5, then its cube ends with 5. (T)
(iv) Cube of a number ending with zero has three zeros at its right. (T)
(v) The cube of a single digit number may be a single digit number. (F)
(vi) There is no perfect cube which ends with 8(F)
(vii) The cube of a two digit number may be a three digit number. (F)

Question 4.
Find the two digit number which is a square number and also a cubic number.
Solution:
The two digited square and cubic
number is 64
∴ 64 = 8 x 8 = 8² ⇒ \(\sqrt{64}\) = 8
64 = 4 x 4 x 4 = 4³ ⇒ \(\sqrt[3]{64}\) = 4