AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.5 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.5
![]()
Question 1.
Find the missing digits in the following additions.
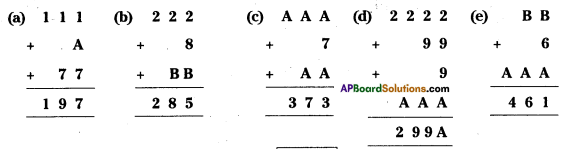
Solution:
a) 1 + A + 7 = 17 ⇒ A = 17 – 8 = 9
∴ A = 9
b) 2 + 8 + B = 15 ⇒ B = 15 – 10 = 5
2 + 1 + B = 8 ⇒ B = 8 – 3 = 5
∴ B = 5
c) A + 7 + A=13 ⇒ 2A = 6 ⇒ A = 3 A + A + 1 = 7 2A = 6 ⇒ A = 3
∴ A = 3
![]()
d) From 1st column
2 + 9 + 9 + A = 26
A = 26 – 20 = 6
From 2nd column
⇒ 2 + 1 + A = 9 ⇒ A = 9 – 3 = 6
∴ A = 6
e) B + 6 + A = 11 or 21
B + A + (1 or 2) = 6
A + 1 = 4 ⇒ A = 3
⇒ From (1), B + 6 + 3 = 11 ⇒ B = 2
∴ A = 3, B = 2
Question 2.
Find the value of A in the following
(a) 7A – 16 = A9 (b) 107 – A9 = lA (e) A36 – 1A4 = 742
Solution:
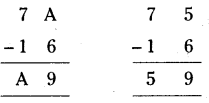
a) 7A – 16 = A9
A- 6 = 9
If A = 5 it is possible.
∴ A = 5 (or)
7A- 16 = A9
⇒ 7 x 10 + (1 x A) – 16 = (A x 10 + 9 x 1)
⇒ 70 + A – 16 = 10A + 9
⇒ 9A = 45
⇒ A = 5
![]()
b) 107 – A9 = 1A
⇒ 107 – (10 x A + 9 x 1) = (1 x 10 + A x 1)
⇒ 107-10A-9= 10 +A
⇒ 11A = 88 A = 8
c) A36 – 1A4 = 742
⇒ (100 x A + 3 x 10 + 6 x 1) – (1 x 100 + A x 10 + 4 x 1) = 742
⇒ 100A + 36 – 100 – 10A – 4 = 742
⇒ 90A = 810
⇒ A = \(\frac{810}{90}\)
∴ A = 9
Question 3.
Find the numerical value of the letters given below-

Solution:
a) If E x 3 = E then E should be equal to 0 (or) 5.
5 x 3 = 15, 0 x 3 = 0
3 x D + 0 = ID [If E = 0]
⇒ 3D = 10 + D
⇒ 2D = 10
⇒ D = 5

∴ F = 1, D = 5, E = 0
![]()
b) If H x 6 = H then H should be equal to 0, 2, 6, 8.
G6 = 1G [If H = 0]
⇒ 6G + 0 = 10 + G
⇒ 5G = 10
⇒ G = 10/5 = 2
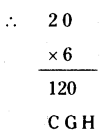
C = 1, G = 2, H = 0
Question 4.
Replace the letters with appropriate digits
(a) 73K ÷ 8 = 9L
(b) 1MN ÷ 3 = MN
Solution:
a) 73K ÷ 8 = 9L
\(\frac{73 \mathrm{~K}}{8}\) = 9L
If 73K is divisible by 8 then K = {1, 2, 3, …………. 9}
Select K = 6 from the set
∴ \(\frac{73 \mathrm{~K}}{8}\) (R = 0)
∴ \(\frac{73 \mathrm{~K}}{8}\) = 92 = 9L
⇒ 90 + 2 = (9 x 10 + L x 1)
⇒ 90 + 2 = 90 + L
∴ L = 2
∴ K = 6, L = 2
![]()
b) 1MN ÷ 3 = MN
If 1MN is divisible by 3 then sum of all the digits is divisible by 3.
⇒ 1 + M + N = 3 x {1,2,3}
Let 1 + M + N = 3 x 2 = 6 say
M + N = 5 …………..(1)
\(\frac{1 \mathrm{MN}}{3}\) = MN
⇒ 1MN = 3[MN]
⇒ 1 x 100 + M x 10 + N x 1
= 3[M x 10 + N x 1]
⇒ 100 + 10M + N = 3[10M + N]
⇒ 100 + 10M + N = 30M + 3N
⇒ 20M + 2N = 100
⇒ 10M + N = 50 …………….. (2)
From (1) & (2)
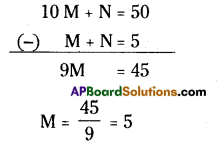
10 M + N = 50 (-) M + N = 5 9M = 45
∴ M = 5
If M = 5 then
M + N = 5
⇒ N = 0
M = 5, N = 0 [∵ \(\frac{150}{3}\) = 50 ]
![]()
Question 5.
If ABB x 999 = ABC 123 (where A, B, C are digits) find the values of A, B, C.
Solution:
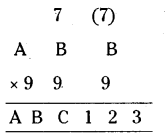
From ABB x 999 = ABC 123, the product of units digit is equal to 3.
∴ B x 9 = 3 is the units digit.
If B = 7 then,
7 x 9 = 6 3

∴ A = 8, B = 7, C = 6
∴ The required product = 876123
∴ A = 8, B = 7, C = 6