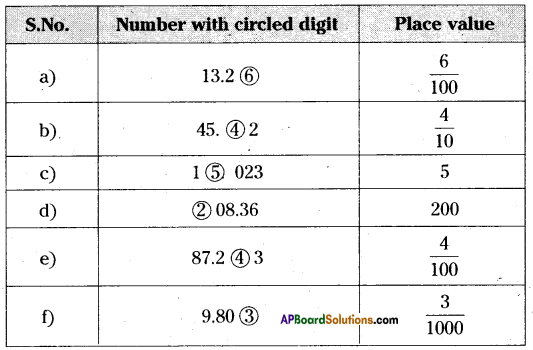
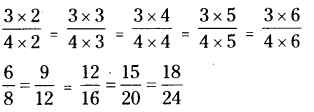AP State Syllabus AP Board 6th Class Maths Solutions Chapter 6 Basic Arithmetic InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 6th Lesson Basic Arithmetic InText Questions

Check Your Progress (Page No. 84)
Question 1.
Express the terms 45 and 70 by using ratio symbol.
Solution:
Given terms are 45 and 70
Ratio = 45 : 70
It can be read as 45 is to 70.
Question 2.
Write antecedent in the ratio 7:15.
Solution:
Given ratio 7 : 15
In the ratio first term is called antecedent.
In 7 : 15 antecedent is 7.
Question 3.
Write the consequent in the ratio 8 : 13.
Solution:
Given ratio 8 : 13
In the ratio second term is called consequent.
In 8 : 13 consequent is 13.

Question 4.
Express the ratio 35 : 55 in the simplest form.
Solution:
Given ratio 35 : 55 (or)
To write the ratio in the simplest form we have to divide by the common factor of two terms 35 and 55.
Common factor is 5.
Now divide by 5,
\(\frac{35}{55}=\frac{35 \div 5}{55 \div 5}=\frac{7}{11}\)
Simplest form of \(\) is \(\frac{7}{11}\)
Question 5.
In the given figure, find the ratio of
i) Shaded part to unshaded parts.
ii) Shaded part to total parts,
iii) Unshaded parts to total parts.

Solution:
i) In the given figur.e,
Number of shaded parts = 1
Number of unshaded parts = 3
Ratio = shaded parts : unshaded parts = 1:3
ii) Number of shaded parts = 1
Total parts = 4
Ratio = shaded parts : total parts = 1:4
iii) Number of unshaded parts = 3
Total parts = 4
Ratio = unshaded parts : total parts = 3:4
Question 6.
Express the following in the form of ratio.
a) The length of a rectangle is triple its breadth. ‘
b) In a school, the workload of teaching 19 sections has been assigned to 38 teachers.
Solution:
a) Let breadth of rectangle = x or one part = 1 part
length of rectangle = triple the breadth
= 3 x x = 3x = 3 parts
Ratio = l : b = x : 3x =\(\frac{1 x}{3 x}=\frac{1}{3}\) = 1:3
b) Given number of sections = 19
Number of teachers = 38
Ratio = 19 : 38 = \(\frac{19}{38}=\frac{1}{2}\) = 1 : 2

(Page No. 88)
Question 1.
Which ratio is larger in the following pairs ?
(a) 5 : 4 or 9 : 8
(b) 12 : 14 or 16 : 18
(c) 8: 20 or 12: 15
(d)4:7 or 7:11
Solution:
a) 5 : 4 or 9 : 8
Write the given ratios as fractions, we have 5 : 4 = \(\frac{5}{4}\) and 9 : 8 = \(\frac{9}{8}\)
Now find the LCM of the denominators of 4 and 8 is 8.
Make the denominator of the each fraction equal to 8.
We have \(\frac{5}{4} \times \frac{2}{2}=\frac{10}{8}\) and \(\frac{9}{8} \times \frac{1}{1}=\frac{9}{8}\)
Clearly we know that 10 > 9
∴ \(\frac{10}{8}>\frac{9}{8}\) (or) 10 : 8 > 9 : 8
10 : 8 is equal to 5 : 4
Therefore the larger ratio is 5 : 4.
b) 12 : 14 or 16:18
12 : 14 = \(\frac{12}{14}=\frac{6}{7}\) and 16 : 18 = \(\frac{16}{18}=\frac{8}{9}\)
Now find the LCM of the denominators of 7 and 9 is 63.
Make the denominator of the each fraction equal to 63.
we have \(\frac{6}{7} \times \frac{9}{9}=\frac{54}{63}\) and \(\frac{8}{9} \times \frac{7}{7}=\frac{56}{63}\)
Clearly, we know that 54 < 56
∴ \(\frac{54}{63}<\frac{56}{63}\) (or) 54:63 < 56:63
56 : 63 is equal to 16 : 18 (or) 8 : 9
∴ The larger ratio is 16 : 18.
c) 8 : 20 or 12 : 15
Write the given ratios as fractions we have
8:20 = \(\frac{8}{20}=\frac{2}{5}\) and 12:15 = \(\frac{12}{15}=\frac{4}{5}\)
\(\frac{2}{5}\) and \(\frac{4}{5}\)
Clearly \(\frac{2}{5}\) < \(\frac{4}{5}\)
i.e., 2:5 < 4 : 5 (or) 8: 20 < 12: 15
Therefore the larger ratio is 12 : 15.

d) 4: 7 or 7: 11
Write the given ratios as fractions, we have 4 7
4 : 7 = \(\frac{4}{7}\) and 7:11 = \(\frac{7}{11}\) .
Now find the LCM of the denominators of 7 and 11 is 77.
Make the denominators of the each fraction equal to 77.
We have \(\frac{4}{7} \times \frac{11}{11}=\frac{44}{77}\) and \(\frac{7}{11} \times \frac{7}{7}=\frac{49}{77}\)
\(\frac{44}{7}\) and \(\frac{49}{77}\)
Clearly we know that 44 < 49
∴ \(\frac{44}{77}<\frac{49}{77}\) (or) 44 : 77 < 49 : 77
i.e.,4: 7 < 7 : 11
Therefore the larger ratio is 7 : 11
Question 2.
Find three equivalent ratios of 12 : 16.
Solution:
Given ratio is 12 : 16
Write the given ratio as fraction we have 12:16= \(\frac{12}{16}=\frac{3}{4}\)
Now, write equivalent fractions of \(\frac{3}{4}\)
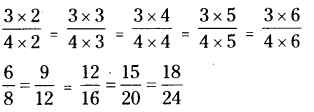
i. e., 6 : 8 = 9 : 12 = 12 : 16 = 15 : 20 = 18 : 24
∴ Equivalent ratios of 12 : 16 are 6 : 8, 9 : 12, 12 : 16, 15 : 20 and 18 : 24.

(Page No. 90)
Question 1.
Check whether the following terms are in proportion ?
1) 5,6,7,8
2) 3,5,6,10
3) 4,8,7,14
4) 2,12,3,18
Solution:
1) Given, 5, 6, 7, 8
If a, b, c, d are in proportion i.e., a : b :: c : d
If 5, 6, 7, 8 are in proportion i.e., 5 : 6 : : 7 : 8
We know that, product of extremes = Product of means [a x d : b x c]
5 x 8 = 6 x 7
40 ≠ 42
So, 5, 6, 7, 8 are not in proportion.
2) Given, 3, 5, 6, 10
If a, b, c, d are in proportion i.e., a : b :: c : d
If 3, 5, 6, 10 are in proportion i.e., 3 : 5 :: 6 : 10
We know that, product of extremes = Product of means a x d = b x c
3 x 10 = 5 x 6
30 = 30
So, 3, 5, 6, 10 are in proportion.
3) Given, 4, 8, 7, 14.
If a, b, c, d are in proportion i.e., a : b : : c : d
If 4, 8, 7, 14 are in proportion i.e., 4 : 8 : : 7 : 14
We know that, product of extremes = Product of means a x d = b x c
4 x 14 = 8 x 7
56 = 56
So, 4, 8, 7, 14 are in proportion.
4) Given, 2, 12, 3, 18
If a, b, c, d are in proportion i.e., a : b :: c : d
If 2, 12, 3, 18 are in proportion i.e., 2 : 12 : : 3 : 18
We know that, product of extremes = Product of means [ a x d = b x c ]
2 x 18 = 12 x 3
36 = 36
So, 2, 12, 3, 18 are in proportion.

Let’s Explore (Page No. 92)
Question 1.
Read the table and fill in the boxes.

Prepare two similar problems and ask your friend to solve them
Solution:
| Weight | Cost of Tomato | Cost of Potato |
| 5 kg | ₹ 75 | ₹ 60 |
| 1 kg | ₹15 | ₹ 12 |
| 3 kg | ₹ 45 | ₹ 36 |
(Page. No. 94)
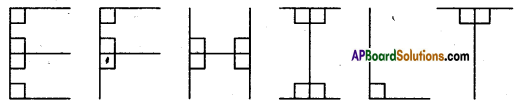
Question 1.
Represent the following in other forms.
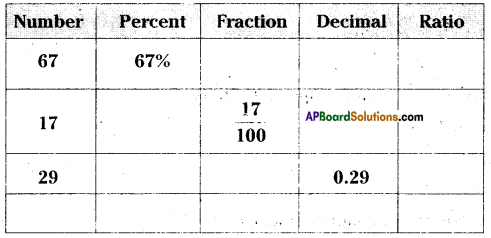
Solution:
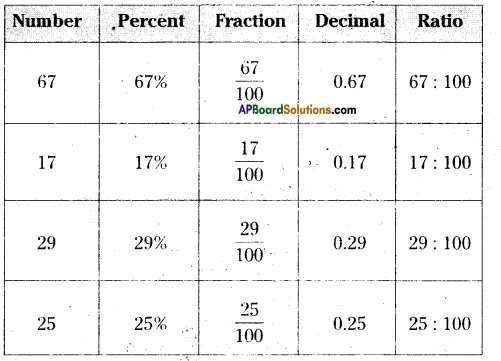
![]()
![]()
![]()


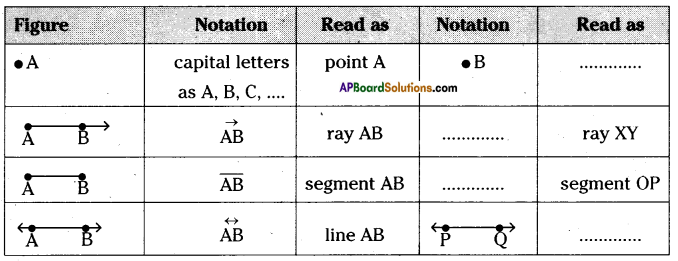
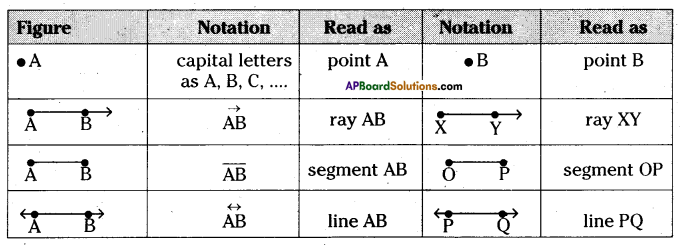
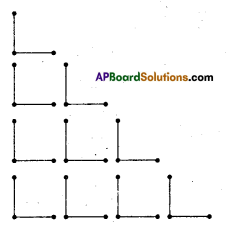
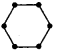
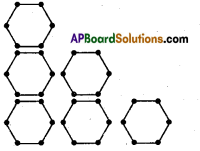
 Continue the same shape for 2 times, 3 times and 4 times. Frame the rule for repeating the pattern.
Continue the same shape for 2 times, 3 times and 4 times. Frame the rule for repeating the pattern.