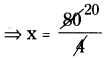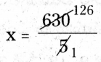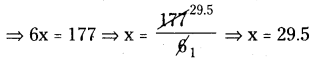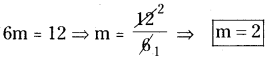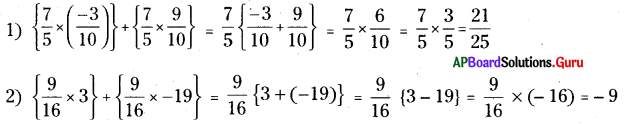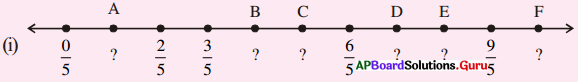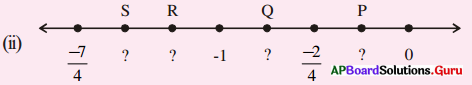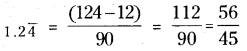Class 8

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.3

కింది ఇవ్వబడిన కొలతలను ఉపయోగించి కావల్సిన – చతుర్భుజాలను నిర్మించండి.

(a) GOLD అనే చతుర్భుజంలో OL = 7.5 సెం.మీ., GL = 6 సెం.మీ., LD = 5 సెం.మీ., DG = 5.5 సెం.మీ. మరియు OD = 10 సెం.మీ
సాధన.
నిర్మాణ క్రమం :
1. 7.5 సెం.మీ. వ్యాసార్థంతో \(\overline{\mathrm{OL}}\) రేఖాఖండాన్ని గీచితిని.
2. O, L లు కేంద్రాలుగా వరుసగా 10 సెం.మీ., 5 సెం.మీ.లతో గీచిన చాపాల ఖండన బిందువును ‘D’ గా గుర్తించితిని.

3. L, D లు కేంద్రాలుగా వరుసగా 6 సెం.మీ., 5.5 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘G’ గా గుర్తించితిని.
4. O, G లను, L, G లను, O, D లను, L, D లను, G, D లను కలిపితిని.
∴ GOLD అను ఒక చతుర్భుజం ఏర్పడినది.

(b) PQRS చతుర్భుజంలో PQ = 4.2 సెం.మీ., QR = 3 సెం.మీ., PS = 2.8 సెం.మీ., PR= 4.5 సెం.మీ. మరియు QS = 5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 4.2 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{PQ}}\) రేఖాఖండాన్ని నిర్మించితిని.

2. P, Qలు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘R’ గా గుర్తించితిని. P, R మరియు Q, Rలను కలిపితిని.
3. Q, Pలు కేంద్రాలుగా వరుసగా 5 సెం.మీ., 2.8 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపరేఖల ఖండన బిందువును ‘S’ గా గుర్తించితిని. P, S లను, Q, S లను, S, Rలను కలిపితిని.
∴ PORS అను ఒక చతుర్భుజం ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.2

కింద ఇవ్వబడిన కొలతలను ఉపయోగించి చతుర్భుజాల నిర్మాణాలను చేయండి.

(a) ABCD చతుర్భుజములో AB = 4.5 సెం.మీ., BC = 5.5 సెం.మీ., CD = 4 సెం.మీ., AD = 6 సెం.మీ., మరియు AC = 7 సెం.మీ.
సాధన.

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంతో ఒక \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. A, B లు కేంద్రాలుగా వరుసగా 7 సెం.మీ., 5.5 సెం.మీ. వ్యాసార్దాలుగా గీచిన చాపాల ఖండన బిందువు ‘C’ గా గుర్తించితిని.
3. A. C లను, B, C లను కలిపితిని.
4. C, A లు కేంద్రాలుగా వరుసగా 4 సెం.మీ., 6 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువు ‘D’ గా గుర్తించితిని.
5. D, C లను, A, D లను కలిపితిని.
∴ ABCD చతుర్భుజం ఏర్పడినది.

(b) PQRS చతుర్భుజములో PQ = 3.5 సెం.మీ., QR = 4 సెం.మీ., RS = 5 సెం.మీ., PS = 4.5 సెం.మీ., మరియు QS = 6.5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 3.5 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{PQ}}\) రేఖాఖండాన్ని గీచితిని.

2. P, Q లు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 6.5 సెం.మీ. లచే రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘S’ గా గుర్తించితిని.
3. S, Q లు కేంద్రాలుగా 5 సెం.మీ., 4 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాలు ఖండించుకొనగా, వాటి ఖండన బిందువును ‘R’ గా గుర్తించితిని.
4. P, S లను Q, S లను కలిపితిని. అదేవిధంగా S, Rలను Q, Rలను కలిపితిని.
∴ చతుర్భుజం PARS ఏర్పడినది.

(c) సమాంతర చతుర్భుజం ABCD లో AB = 6.సెం.మీ., BC = 4.5 సెం.మీ. మరియు BD = 7.5 సెం.మీ.
సాధన.
ABCD సమాంతర చతుర్భుజంలో
AB = CD = 6 సెం.మీ.
BC = AD = 4.5 సెం.మీ.

నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని గీచితిని.
2. A, B లు కేంద్రాలుగా 4.5 సెం.మీ., 7.5 సెం.మీ. వ్యాసార్ధంతో గీచిన చాపాల ఖండన బిందువులను ‘D’ గా గుర్తించితిని. A, D మరియు B, D లను కలిపితిని.
3. D, B లు కేంద్రాలుగా 6. సెం.మీ., 4.5 సెం.మీ. వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువును ‘C’ గా గుర్తించితిని.
4. B, C మరియు D, C లను కలిపితిని.
∴ సమాంతర చతుర్భుజం ABCD ఏర్పడినది.

(d) సమచతుర్భుజం (రాంబస్) NICE లో NI = 4 సెం.మీ. మరియు IE = 5.6 సెం.మీ.
సాధన.
NI = IC = CE = NE = 4 సెం.మీ., IE = 5.6 సెం.మీ.

నిర్మాణ క్రమం :
1. 4 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{NI}}\) రేఖాఖండాన్ని గీచితిని.
2. N, I లు కేంద్రాలుగా వరుసగా 4 సెం.మీ., 5.6 సెం.మీ. వ్యాసార్ధాలతో రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘E’ గా గుర్తించితిని. N, E మరియు I, E లను కలిపితిని.
3. E, Iలు కేంద్రాలుగా వరుసగా 4 సెం.మీ., వ్యాసార్ధాలతో గీచిన రెండు చాపాల ఖండన బిందువును ‘C’ గా గుర్తించితిని.
4. E, C లను, I, C లను కలిపితిని.
∴ NICE రాంబస్ ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.1

కింద ఇవ్వబడిన కొలతలను ఉపయోగించి చతుర్భుజాల నిర్మాణాలను చేయండి. నిర్మాణ క్రమం రాయండి.

(a) ABCD చతుర్భుజంలో AB = 5.5 సెం.మీ., BC = 3.5 సెం.మీ., CD = 4 సెం.మీ., AD = 5 సెం.మీ., మరియు ∠A = 45°.
సాధన.
ABCD చతుర్భుజంలో AB = 5.5 సెం.మీ.,
BC = 3.5 సెం.మీ., CD = 4 సెం.మీ.,
AD = 5 సెం.మీ., A = 45°

నిర్మాణ క్రమం :
1. 5.5 సెం.మీ. వ్యాసార్ధం గల \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని గీచితిని.
2. A కేంద్రంతో 45° కిరణాన్ని, 5 సెం.మీ.ల చాపాన్ని గీయగా వాటి ఖండన బిందువు ‘D’గా గుర్తించితిని.
3. D, B లు కేంద్రాలు వరుసగా 4 సెం.మీ., 3.5 సెం.మీ.ల వ్యాసార్ధాలతో గీచిన చాపాల ఖండన బిందువు ‘C’.
4. DC మరియు BC లను కలిపితిని.
∴ ABCD చతుర్భుజం ఏర్పడినది.

(b) BEST చతుర్భుజంలో BE = 2.9 సెం.మీ., ES = 3.2 సెం.మీ., ST = 2.7 సెం.మీ., BT = 3.4 సెం.మీ., మరియు ∠B = 75°.
సాధన.
BEST చతుర్భుజంలో BE = 2.9 సెం.మీ.,
ES = 3.2 సెం.మీ., ST = 2.7 సెం.మీ.,
BT = 3.4 సెం.మీ., ∠B = 75°

నిర్మాణ క్రమం :
1. 2.9 సెం.మీ. వ్యాసార్థం గల BE రేఖాఖండాన్నినిర్మించితిని.
2. B కేంద్రంగా 75° కోణంతో ఒక కిరణాన్ని, 3.4 సెం.మీ. వ్యాసార్థంతో ఒక చాపాన్ని గీయగా అవి ఖండించుకొన్న ఖండన బిందువు T గా గుర్తించితిని.
3. T, E లు కేంద్రాలుగా 2.7 సెం.మీ., 3.2 సెం.మీ.లతో వరుసగా రెండు చాపాలను గీయగా వాటి ఖండన బిందువు ‘S’ గా గుర్తించితిని.
4. T, S మరియు E, S లను కలిపితిని.
∴ BEST చతుర్భుజం ఏర్పడినది.

(c) సమాంతర చతుర్భుజం PQRS లో PQ = 4.5 సెం.మీ., QR = 3 సెం.మీ. మరియు ∠PQR = 60°.
సాధన.
PQ = 4.5 సెం.మీ., QR = 3 సెం.మీ. మరియు ∠PQR = 60°.
⇒ RS = 4.5 సెం.మీ. మరియు PS = 3 సెం.మీ. [∵ ఎదురెదురు భుజాలు సమానాలు]

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{PQ}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. Q కేంద్రంగా 60° కోణంతో ఒక కిరణాన్ని, 3 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా వాటి ఖండన బిందువును ‘R’ గా గుర్తించితిని.
3. R, P లు కేంద్రాలుగా వరుసగా 4.5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలుగా రెండు చాపాలను గీయగా వాటి ఖండన బిందువు ‘S’ గా గుర్తించితిని.
4. P, Sలను; S, Rలను కలుపగా PQRS సమాంతర చతుర్భుజం ఏర్పడినది.

(d) రాంబస్ MATH లో AT = 4 సెం.మీ., ∠MAT = 120°.
సాధన.
రాంబస్ లో అన్ని భుజాలు సమానాలు కావున
MA = 4 సెం.మీ., AT = 4 సెం.మీ., TH = 4 సెం.మీ., MH = 4 సెం.మీ.,
∠MAT = 120°.

నిర్మాణ క్రమం :
1. 4 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{MA}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. A కేంద్రంగా 120° కోణంతో ఒక కిరణాన్ని, 4 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘T’ గా గుర్తించితిని.
3. M, T లు కేంద్రాలుగా 4 సెం.మీ. వ్యాసార్ధంతో రెండు చాపాలను గీయగా వాటి ఖండన బిందువును ‘H’ గా గుర్తించితిని.
4. M, H లను, T, H లను కలపగా MATH రాంబస్ ఏర్పడినది.

(e) దీర్ఘచతురస్రం FLAT లో FL = 5 సెం.మీ., LA = 3 సెం.మీ.
సాధన.
దీర్ఘచతురస్రం FLAT లో FL = AT = 5 సెం.మీ.,
LA = TF = 3 సెం.మీ., ∠F = ∠L= ∠A = ∠T = 90°

నిర్మాణ క్రమం :
1. 5 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{FL}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. F కేంద్రంగా 90° ల కిరణాన్ని, 3 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీయగా, వాటి ఖండన బిందువును ‘T’ గా గుర్తించితిని.
3. T, L కేంద్రాల నుండి వరుసగా 5 సెం.మీ., 3 సెం.మీ. వ్యాసార్ధాలతో చాపాలు గీయగా ఏర్పడిన ఖండన బిందువును ‘A’ గా గుర్తించితిని.
4. T, A లను, L, A లను కలిపితిని.
∴ FLAT దీర్ఘచతురస్రం ఏర్పడినది.

(f) చతురస్రం LUDO లో LU = 4.5 సెం.మీ.
సాధన.
చతురస్రం LUDO లో LU = UD = DO = LO = 4.5 సెం.మీ.

నిర్మాణ క్రమం :
1. 4.5 సెం.మీ. వ్యాసార్ధంగా LU రేఖాఖండాన్ని గీచితిని.
2. Lకేంద్రంగా 90° కిరణాన్ని మరియు 4. 5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీచితిని. అలాగే U కేంద్రంగా 90° కిరణాన్ని మరియు 4.5 సెం.మీ. వ్యాసార్ధంతో ఒక చాపాన్ని గీచితిని. వాటి ఖండన బిందువులను వరుసగా O,Dలుగా గుర్తించితిని.
3. O, D లను కలిపితిని.
∴ LUDO చతురస్రం ఏర్పడినది.

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు InText Questions

ఇవి చేయండి (పేజీ నెం. 35)

ఈ క్రింది వానిలో ఏవి రేఖీయ సమీకరణాలు :
(i) 4x + 6 = 8
(ii) 4x – 5y = 9
(iii) 5x + 6xy – 4y² = 16
(iv) xy + yz + zx = 11
(v) 3x + 2y – 6 = 0
(vi) 3 = 2x + y
(vii) 7p+ 6q + 13s = 11
సాధన.
(i), (ii), (v), (vi) (vii) లు రేఖీయ సమీకరణాలు ఎందుకనగా ఆ సమీకరణాలలో ప్రతిదాని యొక్క పరిమాణం ఒకటి (1).

ఇవి చేయండి (పేజీ నెం. 36)

ఈ క్రింది వానిలో ఏవి సామాన్య సమీకరణాలు ?
(i) 3x + 5 = 14
(ii) 3x – 6 = x + 2
(iii) 3 = 2x + y
(iv) \(\frac{x}{3}\) + 5 = 0
(v) x² + 5x + 3 = 0
(vi) 5m – 6n = 0
(vii) 7p+ 6q + 13s = 11
(viii) 13t – 26 = 39
సాధన.
(i) 3x + 5 = 14
(ii) 3x – 6 = x + 2
(iv) \(\frac{x}{3}\) + 5 = 0
(viii) 13t – 26 = 39 లు సామాన్య సమీకరణాలు ఎందుకనగా ఇవి ax + b = 0 రూపంలో కలవు.

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.5 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.5

ప్రశ్న 1.
క్రింది సమీకరణాలను సాధించుము.
(i) \(\frac{n}{5}-\frac{5}{7}=\frac{2}{3}\)
సాధన.

(ii) \(\frac{x}{3}-\frac{x}{4}=14\)
సాధన.
\(\frac{4 x-3 x}{12}\) = 14 ⇒ \(\frac{\mathrm{x}}{12}\) = 14
⇒ x = 12 × 14 = 168
∴ x = 168

(iii) \(\frac{z}{2}+\frac{z}{3}-\frac{z}{6}=8\)
సాధన.
\(\frac{3 z+2 z-z}{6}\) = 8

(iv) \(\frac{2 p}{3}-\frac{p}{5}=11 \frac{2}{3}\)
సాధన.

(v) \(9 \frac{1}{4}=y-1 \frac{1}{3}\)
సాధన.

(vi) \(\frac{x}{2}-\frac{4}{5}+\frac{x}{5}+\frac{3 x}{10}=\frac{1}{5}\)
సాధన.

(vii) \(\frac{x}{2}-\frac{1}{4}=\frac{x}{3}+\frac{1}{2}\)
సాధన.

(viii) \(\frac{2 x-3}{3 x+2}=\frac{-2}{3}\)
సాధన.
⇒ 3(2x – 3) = – 2(3x + 2)
⇒ 6x – 9 = – 6x – 4
⇒ 6x + 6x = – 4 + 9
⇒ 12x = 5
∴ x = \(\frac {5}{12}\)

(ix) \(\frac{8 p-5}{7 p+1}=\frac{-2}{4}\)
సాధన.
\(\frac{8 p-5}{7 p+1}=\frac{-1}{2}\)
⇒ 2(8p – 5) = -(7p + 1)
⇒ 16p – 10 = – 7p – 1
⇒ 16p + 7p = – 1 + 10
⇒ 23p = 9
∴ p = \(\frac {9}{23}\)

(x) \(\frac{7 y+2}{5}=\frac{6 y-5}{11}\)
సాధన.
⇒ 11(7y + 2) = 5 (6y – 5)
⇒ 77y + 22 = 30y – 25
⇒ 77y – 30y = – 25 – 22
⇒ 47y = – 47 ⇒ y = \(\frac {-47}{47}\)
∴ y = -1

(xi) \(\frac{x+5}{6}-\frac{x+1}{9}=\frac{x+3}{4}\)
సాధన.

⇒ 4(x + 13) = 18 (x + 3)
⇒ 4x + 52 = 18x + 54
⇒ 4x – 18x = 54 – 52
⇒ – 14x = 2

(xiii) \(\frac{3 t+1}{16}-\frac{2 t-3}{7}=\frac{t+3}{8}+\frac{3 t-1}{14}\)
సాధన.

– 11t – 38t = 34 – 55
= – 49t = – 21

ప్రశ్న 2.
ఒక సంఖ్య యొక్క 3వ భాగము దాని 5వ భాగము కంటే 4 ఎక్కువ అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
x యొక్క 3వ భాగం = \(\frac{x}{3}\)
x యొక్క 5వ భాగం = \(\frac{x}{5}\)

ప్రశ్న 3.
రెండు ధనసంఖ్యల భేదం 36. ఒక దానిని రెండవ దానితో భాగించగా వచ్చే భాగఫలం 4 అయిన వానిని కనుగొనుము.
(సూచన : ఒక సంఖ్య ‘x’ అనుకొనిన రెండవ సంఖ్య ‘x – 36’)
సాధన.
రెండు ధనసంఖ్యలు x, (x – 36) అనుకొనుము.
ఒక దానిని రెండవ దానితో భాగించగా వచ్చు భాగఫలం 4 అయిన
⇒ \(\frac{x}{x-36}\) ⇒ 4 = x = 4(x – 36)
⇒ x = 4x – 144 ⇒ 4x – x = 144
⇒ 3x = 144 ⇒ x = 48
∴ ఆ ధనసంఖ్యలు = x, x – 36 = 48, 12.

ప్రశ్న 4.
ఒక భిన్నంలో లవం, హారం కంటే 4 తక్కువ. అయితే లవ, హారాలకు ఒకటి కలిపిన అది \(\frac {1}{2}\) కు సమానము అవుతుంది. అయిన ఆ భిన్నమును కనుగొనుము.
సాధన.
ఒక భిన్నం \(\frac{x}{y}\) అనుకొనుము.
∴ లవం, హారం కంటే 4 తక్కువ అయిన లవం (x) = y – 4 అగును.
భిన్నం = \(\frac{y-4}{y}\)
లెక్క ప్రకారం \(\frac{y-4+1}{y+1}=\frac{1}{2}\) ⇒ \(\frac{y-3}{y+1}=\frac{1}{2}\)
⇒ 2 = 2(y – 3) = y + 1
⇒ 2(y – 6) = y + 1
⇒ 2y – y = 1 + 6 ⇒ y = 7
∴ కావలసిన భిన్నం = \(\frac{y-4}{y}=\frac{7-4}{7}=\frac{3}{7}\)

ప్రశ్న 5.
మూడు వరుస సంఖ్యలను 10, 17, 26 లచే భాగించినపుడు భాగఫలాల మొత్తం 10ని ఇచ్చే మూడు వరుస సంఖ్యలను కనుగొనుము.
(సూచన : మూడు వరుస సంఖ్యలను x, x + 1, x + 2 అనుకొనిన, \(\frac{x}{10}+\frac{x+1}{17}+\frac{x+2}{26}\) = 10)
సాధన.
మూడు వరుస సంఖ్యలు x, (x + 1), (x + 2) లు అనుకొనుము.,
x, (x + 1), (x + 2) లను 10, 17, 26 లచే
భాగించగా వచ్చు భాగఫలాల మొత్తం 10 అయిన

⇒ 221x + 130x + 130 + 85x + 170 = 22,100
⇒ 436x + 300 = 22,100
⇒ 436x = 22,100 – 300

∴ కావలసిన 3 వరుస సంఖ్యలు = 50, 51, 52.

ప్రశ్న 6.
40 మంది విద్యార్థులు గల తరగతిలో, బాలికల సంఖ్య, బాలుర సంఖ్యలో \(\frac {3}{5}\)వ వంతు అయిన బాలుర సంఖ్యను కనుగొనుము.
సాధన.
తరగతిలోని విద్యార్థుల సంఖ్య = 40
బాలుర సంఖ్య = x అనుకొనుము.

ప్రశ్న 7.
15 సం॥ల తరువాత మేరి వయస్సు, ప్రస్తుత వయస్సుకు 4 రెట్లు. అయిన మేరి ప్రస్తుత వయస్సు ఎంత ?
సాధన.
మేరి ప్రస్తుత వయస్సు = x అనుకొనుము.
15 సం॥ల తరువాత మేరి వయస్సు = (x + 15) సం॥లు
లెక్క ప్రకారం (x + 15) = 4 × x ⇒ x + 15 = 4x
⇒ 4x – x = 15 ⇒ 3x = 15
⇒ x = 5
∴ మేరి ప్రస్తుత వయస్సు = 5 సం॥లు.

ప్రశ్న 8.
అరవింద్ దగ్గర వున్న కిడ్డీ బ్యాంక్ లో రూపాయి నాణెములు, అర్ధ రూపాయి నాణెములు గలవు. అర్ధ రూపాయి నాణెముల సంఖ్య, రూపాయి నాణెముల సంఖ్యకు 3 రెట్లు. నాణెముల మొత్తం విలువ ₹ 35 అయిన ఏఏ రకం నాణెములు ఎన్నెన్ని గలవు ?
సాధన.
రూపాయి నాణేల సంఖ్య = x అనుకొనుము.
అర్ధ రూపాయి నాణేల సంఖ్య = 3 × x = 3x
నాణేల మొత్తం విలువ = ₹ \(\frac{3 x}{2}\) + x
∴ లెక్క ప్రకారం \(\frac{3 x}{2}\) + x = 35

∴ రూపాయి నాణేల సంఖ్య = 14
అర్ధ రూపాయి నాణేల సంఖ్య = 3x = 3 × 14 = 42

ప్రశ్న 9.
A మరియు B లు కలసి ఒక పనిని 12 రోజులలో పూర్తి చేయగలరు. A ఒక్కడే ఆ పనిని 20 రోజులలో పూర్తి చేసిన B ఒక్కడే ఆ పనిని ఎన్ని రోజులలో పూర్తి చేయగలడు ?
సాధన.
A, B లు ఒక పనిని 12 రోజులలో పూర్తి చేయగలిగిన,
వారు ఇరువురూ ఒక రోజులో చేసే పని = \(\frac {1}{2}\)
A అదే పనిని 20 రోజులలో పూర్తి చేయగలిగిన, అతని 1 రోజు పని = \(\frac {1}{20}\)
∴ B ఒక రోజు పని = \(\frac{1}{12}-\frac{1}{20}\)
= \(\frac{5-3}{60}\)
= \(\frac {2}{60}\)
= \(\frac {1}{30}\) వ వంతు
∴ ఆ పనిని పూర్తి చేయుటకు B కి పట్టు రోజులు = 30 రోజులు

ప్రశ్న 10.
ఒక రైలు 40 కి.మీ./గంట వేగంతో ప్రయాణించిన గమ్యస్థానమును 11 నిమిషాలు ఆలస్యంగా చేరును. ఒకవేళ 50 కి.మీ./గంట వేగంతో ప్రయాణించిన 5 నిమిషాలు ఆలస్యంగా చేరును. అయిన రైలు ప్రయాణించవలసిన దూరమును కనుగొనుము.
సాధన.
చేరవలసిన గమ్యస్థానం యొక్క దూరం = x కి.మీ. అనుకొనుము.
40 కి.మీ./గంట వేగంతో ‘x’ కి.మీ. ప్రయాణించుటకు పట్టు కాలం = \(\frac{x}{40}\) గం॥
50 కి.మీ./గంట వేగంతో ప్రయాణించుటకు పట్టు కాలం = \(\frac{x}{50}\) గం॥
కానీ దత్తాంశం ప్రకారం ఈ రెండింటి మధ్య తేడా = 11 – 5 = 6 ని॥ = \(\frac{6}{60}\) గంటలు

ప్రశ్న 11.
ఒక జింకల గుంపులో \(\frac{1}{4}\)వ భాగము అడవికి వెళ్ళినాయి. మొత్తంలో \(\frac{1}{3}\) వ భాగము పచ్చిక మైదానంలో వున్నాయి. మిగిలిన 15 నది ఒడ్డున నీరు త్రాగుతున్నాయి. అయిన మొత్తం జింకల సంఖ్యను కనుగొనుము.
సాధన.
జింకల సంఖ్య = x అనుకొనుము.
అడవికి వెళ్ళిన జింకల సంఖ్య = \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
పచ్చిక మైదానంలోని జింకల సంఖ్య = \(\frac{1}{4}\) × x = \(\frac{1}{4}\)
∴ మిగిలిన జింకల సంఖ్య =

కాని, లెక్క ప్రకారం మిగిలిన జింకల సంఖ్య = 15
∴ \(\frac{5 x}{12}\) = 15

∴ మొత్తం జింకల సంఖ్య = 36

ప్రశ్న 12.
ఒక దుకాణదారుడు ఒక రేడియోను ₹ 903 లకు అమ్మటం వల్ల అతను 5% లాభాన్ని పొందుతాడు. అయిన రేడియో యొక్క కొన్నవెలను కనుగొనుము.
సాధన.
రేడియో అమ్మినవెల (S.P.) = ₹ 903
లాభశాతం = 5%
కోన్నవెల (C.P.) = ?

ప్రశ్న 13.
శేఖర్ తన వద్ద వున్న మిఠాయిలలో పావు భాగము రేణుకు, 5 మిఠాయిలు రాజికి ఇచ్చాడు. ఇంకా తన వద్ద 7 మిఠాయిలు మిగిలి వున్న అతని వద్ద మొదట వున్న మిఠాయిలు ఎన్ని ?
సాధన.
శేఖర్ వద్ద వున్న మిఠాయిల సంఖ్య = x అనుకొనుము.
రేణుకకు ఇచ్చిన భాగం = \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
రాజికి ఇచ్చిన మిఠాయిల సంఖ్య = 5
ఇంకా తన వద్ద నున్న మిఠాయిల సంఖ్య = 7
లెక్క ప్రకారం


∴ శేఖర్ వద్ద మొదట ఉన్న మిఠాయిల సంఖ్య = 16

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.4 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.4

ప్రశ్న 1.
l // m అయిన క్రింది పటంలో ‘x’ విలువను కనుగొనుము.

సాధన.
l // m కావున 3x – 10° = 2x + 15° అగును
[∵ అభిముఖ కోణాలు సమానాలు]
⇒ 3x – 10 = 2x + 15
⇒ 3x – 2x = 15 + 10
∴ x = 25°

ప్రశ్న 2.
ఒక సంఖ్య యొక్క 8 రెట్ల నుండి 10ని తగ్గించిన వచ్చే విలువ, అదే సంఖ్య యొక్క 6 రెట్లు మరియు 4ల మొత్తం విలువకు సమానము. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
‘x’కు 8 రెట్ల సంఖ్య = 8 × x = 8x
8x నుండి 10 తగ్గించగా వచ్చు సంఖ్య = 8x – 10
x కు 6రెట్ల సంఖ్య = 6 × x = 6x
6x మరియు 4ల మొత్తం = 6x + 4
∴ లెక్క ప్రకారం
8x – 10 = 6x + 4
⇒ 8x – 6x = 4 + 10 ⇒ 2x = 14 ⇒ x = 7.
∴ కావలసిన సంఖ్య = 7

ప్రశ్న 3.
ఒక రెండంకెల సంఖ్యలో రెండు అంకెల మొత్తము 9. ఈ సంఖ్య నుండి 27ను తీసివేసిన సంఖ్యలోని అంకెలు తారుమారు అవుతాయి. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
రెండంకెల సంఖ్యలో ఒకట్ల స్థానంలోని అంకె = x అనుకొనుము
రెండు అంకెల మొత్తం = 9
∴ పదుల స్థానంలోని అంకె = 9 – x
ఆ సంఖ్య = 10(9 – x) + x
= 90 – 10x + x
= 90 – 9x
ఆ సంఖ్య నుండి 27ను తీసివేసిన అంకెలు తారుమారు అవుతాయి.
∴ (90 – 9x) – 27 = 10x + (9 – x)
63 – 9x = 9x + 9
9x + 9x = 63 – 9
18x = 54 ⇒ x = \(\frac {54}{18}\) = 3
∴ ఒకట్ల స్థానములోని అంకె = 3
పదుల స్థానములోని అంకె = 9 – 3 = 6
∴ ఆ సంఖ్య = 63

ప్రశ్న 4.
ఒక సంఖ్యను 5 : 3 నిష్పత్తిలో రెండు భాగాలుగా విభజించారు. ఒక భాగము రెండవ భాగం కంటే 10 ఎక్కువ. అయిన ఆ సంఖ్యను, రెండు భాగాలను
కనుగొనుము.
సాధన.
ఒక సంఖ్యను 5 : 3 నిష్పత్తిలో రెండు భాగాలుగా విభజించిన ఆ సంఖ్యలు 5x, 3x అనుకొనుము.
∴ 5x = 3x + 10
[∵ ఒక భాగం మరొక భాగం కంటే 10 ఎక్కువ కనుక)
⇒ 5x – 3x = 10
2x = 10
x = 5
∴ కావలసిన సంఖ్య = 5x + 3x = 8x
= 8 × 5= 40
ఆ సంఖ్యలోని భాగాలు = 5x = 5 × 5 = 25
= 3x = 3 × 5 = 15

ప్రశ్న 5.
నేను ఒక సంఖ్యను 3 రెట్లు చేసి 2 కలిపినపుడు వచ్చిన ఫలితము, అదే సంఖ్యను 50 నుంచి తీసివేసినపుడు వచ్చిన ఫలితము సమానము. అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య = x అనుకొనుము.
⇒ xకు 3 రెట్ల సంఖ్య = 3 × x = 3x
3x కు 2 కలిపిన వచ్చు ఫలితము = 3x + 2
xను 50 నుంచి తీసివేసిన వచ్చు సంఖ్య = 50 – x
∴ లెక్క ప్రకారం
⇒ 3x + 2 = 50 – x
⇒ 3x + x = 50 – 2
⇒ 4x = 48
⇒ x = 12
∴ కావలసిన సంఖ్య = 12

ప్రశ్న 6.
మేరి వయస్సు వారి సోదరి వయస్సుకు రెట్టింపు. 5 సం॥ల అనంతరం మేరి వయస్సు వాళ్ళ సోదరి వయస్సు కంటే 2 సం॥లు ఎక్కువ. అయిన వారిరువురి వయస్సును కనుగొనుము.
సాధన.
మేరి సోదరి వయస్సు = x సం॥లు అనుకొనుము.
మేరి వయస్సు = 2 × x
= 2x సం॥లు
5 సం॥ల తరువాత సోదరి వయస్సు = (x + 5) సం॥లు
5 సం॥ల తరువాత మేరి వయస్సు = (2x + 5) సం॥లు
లెక్క ప్రకారం
⇒ 2x + 5 = x + 5 + 2
⇒ 2x = x + 2 ⇒ 2x – x = 2 ⇒ x = 2
∴ మేరి సోదరి వయస్సు (x) = 2 సం॥
∴ మేరి వయస్సు = 2x = 2 × 2 = 4 సం॥లు.

ప్రశ్న 7.
5 సం॥ల అనంతరం రేష్మ వయస్సు 9 సం॥ల క్రితం ఆమె వయస్సుకు 3 రెట్లు. అయిన ఆమె ప్రస్తుత వయస్సు ఎంత ?
సాధన.
రేష్మ ప్రస్తుత వయస్సు = x సం॥లు అనుకొనుము.
5 సం॥ అనంతరం రేష్మ వయస్సు = (x + 5) సం॥
9 సం॥ల క్రితం రేష్మ వయస్సు = (x – 9) సం॥
లెక్క ప్రకారం x + 5 = 3(x – 9) = 3x – 27
x – 3x = – 27 – 5
– 2x = – 32 ⇒ x = \(\frac {-32}{-2}\) = 16
∴ రేష్మ ప్రస్తుత వయస్సు = 16 సం॥లు.

ప్రశ్న 8.
ఒక పట్టణ జనాభా 1200 పెరిగిన తరువాత ప్రస్తుత జనాభాలో 11% తగ్గింది. ఇప్పుడు ఆ పట్టణ జనాభా మొదట ఉన్న జనాభా కన్నా 32 తక్కువ. అయిన మొదట ఆ పట్టణ జనాభా ఎంత ?
సాధన.
పట్టణ జనాభా 1200 పెరిగిన తరువాత = x అనుకొనుము.
జనాభాలో 11% = 11% of x = \(\frac{11 x}{100}\)
లెక్క ప్రకారం

∴ పట్టణ జనాభా 1200 పెరిగిన తరువాత = 11,200
∴ పట్టణ ప్రస్తుత జనాభా = 11,200 – 1,200
= 10,000

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.3

క్రింది సమీకరణాలను సాధించుము.

ప్రశ్న 1.
7x – 5 = 2x
సాధన.
7x – 5 = 2x
⇒ 7x – 2x = 5

ప్రశ్న 2.
5x – 12 = 2x – 6
సాధన.
5x – 12 = 2x – 6
⇒ 5x – 2x = – 6 + 12

ప్రశ్న 3.
7p – 3 = 3p +8
సాధన.
7p – 3 = 3p + 8
⇒ 7p – 3p = 8 + 3
⇒ 4p = 11
∴ P = \(\frac {11}{4}\)

ప్రశ్న 4.
8m + 9 = 7m +8
సాధన.
8m + 9 = 7m + 8
⇒ 8m – 7m = 8 – 9
∴ m = -1

ప్రశ్న 5.
7z + 13 = 2z + 4
సాధన.
7z + 13 = 2z + 4
⇒ 72 – 2z = 4 – 13
⇒ 52 = -9
∴ z = \(\frac {-9}{5}\)

ప్రశ్న 6.
9y + 5 = 15y – 1
సాధన.
9y + 5 = 15y – 1
⇒ 9y – 15y = – 1 – 5

ప్రశ్న 7.
3x + 4 = 5 (x – 2)
సాధన.
3x + 4 = 5 (x – 2)
⇒ 3x + 4 = 5x – 10
⇒ 3x – 5x = – 10 – 4
⇒ -2x = – 14
∴ x = 7

ప్రశ్న 8.
3 (t – 3) = 5 (2t – 1)
సాధన.
3(t – 3) = 5 (2t – 1)
= 3t – 9 = 10t – 5
⇒ 3t – 10t = – 5 + 9
⇒ -7t = 4
∴ t = \(\frac {-4}{7}\)

ప్రశ్న 9.
5 (p – 3) = 3 (p – 2)
సాధన.
5 (p – 3) = 3 (p – 2)
⇒ 5p – 15 = 3p – 6
⇒ 5p – 3p = – 6 + 15
⇒ 2p = 9
∴ P = \(\frac {9}{2}\)

ప్రశ్న 10.
5 (z + 3) = 4 (2z + 1)
సాధన.
5 (z + 3) = 4 (2z + 1)
⇒ 5z + 15 = 8z + 4
⇒ 5z – 8z = 4 – 15
⇒ – 3z = -11 ⇒ z = \(\frac {-11}{-3}\)
∴ z = \(\frac {11}{3}\)

ప్రశ్న 11.
15 (x – 1) + 4(x + 3) = 2 (7 + x)
సాధన.
15(x – 1) + 4(x + 3) = 2 (7 + x)
⇒ 15x – 15 + 4x + 12 = 14 + 2x
⇒ 19x – 3 = 14 + 2x
⇒ 19x – 2x = 14 + 3

ప్రశ్న 12.
3(5z – 7) + 2(9z – 11) = 4 (8z – 7) – 111
సాధన.
3 (5z – 7) + 2 (9z – 11) = 4 (8z – 7) – 111
⇒ 152 – 21 + 18z – 22 = 32z – 28 – 111
⇒ 33z – 43 = 32z – 139
⇒ 33z – 32z = – 139 + 43
∴ z = – 96

ప్రశ్న 13.
8 (x – 3) – (6 – 2x) = 2 (x + 2) – 5 (5 – x)
సాధన.
8 (x – 3) – (6 – 2x) = 2 (x + 2) -5 (5 – x)

⇒ 8x – 30 = 5x – 21
⇒ 8x – 5x = -21 + 30
⇒ 3x = 9
⇒ x = 3

ప్రశ్న 14.
3(n – 4) + 2 (4n – 5) = 5 (n + 2) + 16
సాధన.
3 (n – 4) + 2 (4n – 5) = 5 (n + 2) + 16
⇒ 3n – 12 + 8n – 10 = 5n + 10 + 16
⇒ 11n – 22 = 5n + 26
⇒ 11n – 5n = 26 + 22
⇒ 6n = 48

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.2

ప్రశ్న 1.
క్రింది పటాలలో ‘x’ విలువను కనుగొనుము.


సాధన.
i) ఒక త్రిభుజంలోని బాహ్య కోణం, దాని అంతరాభి ముఖ కోణాల మొత్తానికి సమానం.
∴ ∠ACD = ∠B + ∠A
⇒ 123° = x + 56°
⇒ x = 123° – 56° = 67°
∴ x = 67°

ii) త్రిభుజంలోని మూడు కోణాల మొత్తం = 180°
= ∠P + ∠Q + ∠R = 180°
⇒ 45° + 3x + 16° + 68° = 180°
⇒ 3x + 129° = 180°
⇒ 3x = 180 – 129 = 51°

∴ ∠x = 17°

iii) ∠A + ∠B + ∠C = 180°
⇒ 25° + x + 30° = 180°
⇒ x + 55° = 180°
⇒ x = 180 – 55 = 125°
∴ x = 125°

iv) ΔXYZ లో \(\overline{\mathrm{XY}}=\overline{\mathrm{XZ}}\) కావున
∠Y = ∠Z అవుతుంది.
∴ 2x + 7° = 45°
⇒ 2x = 45 – 7 ⇒ 2x = 38

∴ x = 19°

v) ΔBOA నుండి
AB = AO ⇒ ∠B = ∠O = 3x + 10°
ΔCOD నుండి
OC = CD ⇒ ∠O = ∠D = y అనుకొనుము.
∴ ∠C + ∠O + ∠D = 180°
⇒ 2x + y + y = 180°
⇒ 2y = 180 – 2x
y = \(\frac{180-2 x}{2}\) = 90 – x
∴ ∠O = ∠D = 90 – x
కాని ∠BOA = ∠COD [∵ శీర్షాభిముఖ కోణాలు సమానం]
⇒ 3x + 10 = 90 – x
⇒ 3x + x = 90 – 10
⇒ 4x = 80

∴ x = 20°

ప్రశ్న 2.
రెండు సంఖ్యల భేదం 8. పెద్దసంఖ్యకు 2 కలిపిన ఫలితము చిన్న సంఖ్యకు 3 రెట్లు అవుతుంది. ఆ సంఖ్యలను కనుగొనుము.
సాధన.
పెద్ద సంఖ్య = x అనుకొనుము.
రెండు సంఖ్యల భేదం = 8
∴ చిన్న సంఖ్య = x – 8
పెద్ద సంఖ్యకు 2 కలిపిన ఫలితము చిన్న సంఖ్యకు 3 రెట్లు అవుతుంది.
x + 2 = 3(x – 8)
x + 2 = 3x – 24
3x – x = 2 + 24
2x = 26 ⇒ x = \(\frac {26}{2}\) = 13
∴ పెద్ద సంఖ్య = 13
చిన్న సంఖ్య = 13 – 8 = 5

ప్రశ్న 3.
మొత్తం 58, భేదం 28 అయ్యే రెండు సంఖ్యలను కనుగొనుము.
సాధన.
పెద్ద సంఖ్య = x అనుకొనుము.
రెండు సంఖ్యల మొత్తం 58
∴ చిన్న సంఖ్య = 58 – x
ఆ రెండు సంఖ్యల భేదం = 28
∴ x – (58 – x) = 28
x – 58 + x = 28
2x = 28 + 58 = 86 ⇒ x = \(\frac {86}{2}\) = 43
∴ ఒక సంఖ్య లేదా, పెద్ద సంఖ్య = 43
రెండవ సంఖ్య లేదా చిన్న సంఖ్య = 58 – 43 = 15

ప్రశ్న 4.
రెండు వరుస బేసిసంఖ్యల మొత్తం 56 అయిన వాటిని కనుగొనుము.
సాధన.
రెండు వరుస బేసిసంఖ్యలు 2x + 1, 2x + 3 అనుకొనుము.
∴ రెండు బేసిసంఖ్యల మొత్తం = 2x + 1 + 2x + 3 = 56
⇒ 4x + 4 = 56
4x = 56 – 4 = 52 ⇒ x = \(\frac {52}{4}\) = 13
∴ 2x + 1 = 2 × 13 + 1 = 26 + 1 = 27
2x + 3 = 2 × 13 + 3 = 26 + 3 = 29
∴ కావలసిన వరుస బేసిసంఖ్యలు = 27, 29.

ప్రశ్న 5.
మూడు వరుస యొక్క గుణకాల మొత్తం 777. ఆ గుణకాలను కనుగొనుము.
(సూచన : మూడు వరుస 7 యొక్క గుణకాలు ‘x’, ‘x + 7’, ‘x + 14)
సాధన.
7 యొక్క మూడు వరుస గుణకాలు
x, x + 7, x + 14
∴ x + x + 7 + x + 14 = 777
⇒ 3x + 21 = 777
⇒ 3x = 777 – 21
⇒ 3x = 756
∴ x = \(\frac {756}{3}\) = 252
x + 7 = 252 + 7 = 259
x + 14 = 252 + 14 = 266
∴ కావలసిన మూడు వరుస 7 యొక్క గుణకాలు 252, 259, 266.

ప్రశ్న 6.
ఒక మనిషి కాలినడకన 10 కి.మీ. ప్రయాణించిన అనంతరం కొంత దూరము రైలులో, మరికొంత దూరము బస్సులో ప్రయాణించాడు. బస్సులో ప్రయాణించిన దూరము రైలులో ప్రయాణించిన దూరమునకు రెట్టింపు. అతని మొత్తం ప్రయాణం 70 కి.మీ. అయిన అతను రైలులో ప్రయాణించిన దూరము ఎంత ?
సాధన.
కాలినడకన ప్రయాణించిన దూరం = 10 కి.మీ.
రైలులో ప్రయాణించిన దూరం = xకి.మీ. అనుకొనుము
బస్సులో ప్రయాణించిన దూరం = 2 × x = 2x కి.మీ.
∴ 10 + x + 2x = 70
⇒ 3x = 70 – 10
⇒ 3x = 60 ⇒ x = \(\frac {60}{3}\) = 20
∴ రైలులో ప్రయాణించిన దూరం = x = 20 కి.మీ.

ప్రశ్న 7.
వినయ్ ఒక పిజ్జా కొని దానిని మూడు ముక్కలు చేశాడు. వీటిని బరువు తూయగా మొదటిది రెండవదాని కంటే 7గ్రా. తక్కువగాను, మూడవ దానికంటే 4 గ్రా. ఎక్కువ గానూ వుంది. పిజ్జా యొక్క మొత్తం బరువు 300 గ్రా, అయిన ప్రతీ ముక్క బరువును కనుగొనుము.
(సూచన : మొదటి ముక్క బరువు ‘x’ గ్రా. అనుకొనిన పెద్ద దాని బరువు ‘x + 7’, చిన్నదాని బరువు ‘x – 4’ గ్రా.)

సాధన.
ఒక పిజ్జాను 3 ముక్కలు చేసిన
మొదటి ముక్క బరువు = x గ్రా. అనుకొనుము.
పెద్దముక్క బరువు = (x + 7) గ్రా.
చిన్నముక్క బరువు = (x – 4) గ్రా.
∴ x + (x + 7) + (x – 4) = 300
⇒ 3x + 3 = 300
⇒ 3x = 300 – 3 = 297
⇒ x = \(\frac {297}{3}\) = 99
∴ x = 99
x + 7 = 99 + 7 = 106
x – 4 = 99 – 4 = 95
∴ పిజ్జా యొక్క 3 ముక్కల బరువులు 95 గ్రా., 99 గ్రా., 106 గ్రా.

ప్రశ్న 8.
ఒక దీర్ఘచతురస్రాకార పొలము చుట్టుకొలత 400 మీటర్లు. దాని పొడవు, వెడల్పు కంటే 26మీ. ఎక్కువ. అయిన దాని పొడవు, వెడల్పులను కనుగొనుము.
సాధన.
దీర్ఘచతురస్రాకార పొలం వెడల్పు = x మీ.
పొడవు = (x + 26) మీ.
∴ దీ.చ. పొలం చుట్టుకొలత = 2(l + b) = 400
⇒ l + b = 200
⇒ x + 26 + x = 200
⇒ 2x = 200 – 26 = 174
⇒ x = \(\frac {174}{2}\) = 87
∴ దీ.చ. పొలం పొడవు = x + 26
= 87 + 26 = 113 మీ.
వెడల్పు = x = 87 మీ.

ప్రశ్న 9.
ఒక దీర్ఘచతురస్రాకార పొలం యొక్క పొడవు, వెడల్పు యొక్క రెట్టింపు కంటే 8 మీ. తక్కువ. పొలము యొక్క చుట్టుకొలత 56 మీ. అయిన దాని పొడవు, వెడల్పులను కనుగొనుము.
సాధన.
దీర్ఘచతురస్రాకార పొలం వెడల్పు = xమీ. అనుకొనుము
∴ పొడవు = 2 × x – 8
= (2x – 8) మీ.
∴ దీ.చ. పొలం చుట్టుకొలత = 56 మీ.
∴ 2(l + b) = 56
⇒ 2(2x – 8 + x) = 56

∴ దీర్ఘచతురస్రాకార పొలం వెడల్పు (x) = 12 మీ.
దీర్ఘచతురస్రాకార పొలం పొడవు = 2x – 8
= 2 × 12 – 8
= 24 – 8
= 16 మీ.

ప్రశ్న 10.
ఒక త్రిభుజంలోని రెండు భుజాల కొలతలు సమానం. వీని కొలత మూడవ భుజం రెట్టింపు కంటే 5 మీ. తక్కువ. త్రిభుజం యొక్క చుట్టుకొలత 55 మీ. అయిన భుజాల కొలతలను కనుగొనుము.
సాధన.
త్రిభుజంలోని మూడవ భుజం కొలత = x మీ. అనుకొనుము.
∴ మిగిలిన రెండు సమాన భుజాల కొలతలు = 2 × x – 5
= (2x – 5) మీ.
త్రిభుజం చుట్టుకొలత = 55 మీ.
∴ (2x – 5) + (2x – 5) + x = 55
⇒ 5x – 10 = 55 ⇒ 5x = 65
⇒ x = \(\frac {65}{5}\)
∴ x = 13 మీ.
2x – 5 = 2 × 13 – 5 = 26 – 5 = 21 మీ.
∴ ఆ త్రిభుజ మూడు భుజాల కొలతలు = 13, 21, 21 (మీటర్లలో)

ప్రశ్న 11.
రెండు పూరక కోణాల భేదము 12° అయిన వానిని కనుగొనుము.
సాధన.
రెండు పూరక కోణాలలో ఒక కోణం = x అనుకొనుము.
రెండు పూరక కోణాల మొత్తం = 90°
∴ రెండవ కోణం = 90° – x
రెండు పూరక కోణాల భేదం = 12°
∴ x – (90° – x) = 12°
x – 90° + x = 12°
2x = 12° + 90° = 102°
∴ x = \(\frac{102^{\circ}}{2}\) = 51°
∴ ఒక కోణం = 51°
రెండవ కోణం = 90° – 51° = 39°

ప్రశ్న 12.
రాహుల్ మరియు లక్ష్మీల వయస్సుల నిష్పత్తి 5 : 7. నాలుగు సం॥ల తరువాత వారి వయస్సుల మొత్తము 56 సం॥లు. వారి ప్రస్తుత వయస్సులు ఎంత ?
సాధన.
రాహుల్ మరియు లక్ష్మిల వయస్సుల నిష్పత్తి = 5 : 7
వారి వయస్సులు 5x, 7x సం॥లు అనుకొనుము.
4 సం॥ల తరువాత రాహుల్ వయస్సు = 5x + 4
4 సం॥ల తరువాత లక్ష్మి వయస్సు = 7x + 4
లెక్క ప్రకారం
4 సం॥ల తరువాత వారి వయస్సుల మొత్తం = 56
⇒ (5x + 4) + (7x + 4) = 56
⇒ 12x + 8 = 56
⇒ 12x = 48
⇒ x = 4
∴ రాహుల్ వయస్సు = 5x = 5 × 4 = 20 సం॥లు
∴ లక్ష్మి వయస్సు = 7x = 7 × 4 = 28 సం॥లు

ప్రశ్న 13.
ఒక పరీక్షలో 180 బహుళైచ్ఛిక ప్రశ్నలు కలవు. ప్రతి సరియైన సమాధానమునకు 4 మార్కులు ఇవ్వబడును. సమాధానము వ్రాయని మరియు తప్పుగా సమాధానము వ్రాసిన ప్రతి ప్రశ్నకు ఒక మార్కు తగ్గించబడుతుంది. ఒక అభ్యర్థికి ఈ పరీక్షలో 450 మార్కులు వచ్చిన ఆ అభ్యర్థి ఎన్ని ప్రశ్నలకు సరియైన సమాధానములు వ్రాసినాడు ?
సాధన.
సరియైన సమాధానాలు వ్రాసిన ప్రశ్నల సంఖ్య = x అనుకొనిన
తప్పు సమాధాన ప్రశ్నలు = 180 – x
ప్రతి సరియైన సమాధానమునకు 4 మార్కులు కనుక సరియైన సమాధానానికి వచ్చు మార్కులు = 4 × x = 4x
తప్పు సమాధానముకు తగ్గించే మార్కులు = (180 – x) × 1 = 180 – x
లెక్క ప్రకారం మొత్తం మార్కులు = 450
∴ 4x – (180 – x) = 450
⇒ 4x – 180 + X = 450
⇒ 5x = 450 + 180 ⇒ 5x = 630

∴ x = 126
∴ సరియైన సమాధానాలు వ్రాసిన ప్రశ్నల సంఖ్య = 126

ప్రశ్న 14.
₹ 5 నోట్లు, ₹ 10 నోట్లు కలిపి మొత్తం 90 నోట్లు కలవు. వీని మొత్తం విలువ ₹ 500 అయిన ఏ రకమైన నోట్లు ఎన్ని కలవు ?
(సూచన : ₹ 5 యొక్క నోట్ల సంఖ్య ‘x’ అనుకొనిన ₹ 10 యొక్క నోట్ల సంఖ్య = 90 – x)
సాధన.
₹ 5 నోట్ల సంఖ్య = x
₹ 10 నోట్ల సంఖ్య = 90 – x అనుకొనుము.
5x + 10(90 – x) = 500
5x + 900 – 10x = 500
– 5x = – 400 ⇒ x = 80
∴ ₹ 5 నోట్ల సంఖ్య = 80
₹ 10 నోట్ల సంఖ్య = 90 – x = 90 – 80 = 10

ప్రశ్న 15.
ఒక వ్యక్తి పెన్నులు, పెన్సిళ్ళు కొనడానికి ₹ 564 ఖర్చు చేశాడు. ఒక్కొక్క పెన్ను ఖరీదు ₹ 7, పెన్సిల్ ఖరీదు ₹ 3, మరియు మొత్తము పెన్నులు, పెన్సిళ్ల సంఖ్య 108 అయిన అతను ఏ రకమైన వస్తువులను ఎన్నెన్ని కొన్నాడు?

సాధన.
పెన్నుల సంఖ్య = x అనుకొనుము.
మొత్తం వస్తువుల సంఖ్య = 108
∴ పెన్సిళ్ళ సంఖ్య = 108 – x
పెన్నుల ఖరీదు = ₹ 7
∴ x పెన్నుల ఖరీదు = ₹7 × x = ₹7x
పెన్సిళ్ళ ఖరీదు = ₹ 3
∴ (108 – x) పెన్సిళ్ళ ఖరీదు = ₹ 3 (108 – x)
= ₹ (324 – 3x)
మొత్తం వస్తువులు కొనడానికి ఖర్చు చేసినది = ₹ 564
∴ 7x + (324 – 3x) = 564
⇒ 7x + 324 – 3x = 564
4x = 564 – 324 = 240 ⇒ x = \(\frac {240}{4}\) = 60
∴ పెన్నుల సంఖ్య = 60
ఈ పెన్సిళ్ళ సంఖ్య = 108 – 60 = 48

ప్రశ్న 16.
ఒక పాఠశాలలోని వాలీబాల్ కోర్టు యొక్క చుట్టుకొలత ను 177 అడుగులు. దీని పొడవు, వెడల్పుకు రెట్టింపు అయిన వాలీబాల్ కోర్టు యొక్క పొడవు, వెడల్పులను కనుగొనుము.

సాధన.
వాలీబాల్ కోర్టు యొక్క వెడల్పు = x అడుగులు అనుకొనుము.
∴ పొడవు = 2 × x = 25 అడుగులు
కోర్టు చుట్టుకొలత = 177 అడుగులు
∴ 2(l + b) = 177
⇒ 2(2x + x) = 177
⇒ 2 × 3x = 177

∴ వాలీబాల్ కోర్టు వెడల్పు = x = 29.5 అడుగులు
పొడవు = 2x = 2 × 29.5 = 59 అడుగులు

ప్రశ్న 17.
ఒక పుస్తకము తెరచి వుంది. తెరిచిన ఆ రెండు పేజీలలో పేజీ నెంబర్ల మొత్తము 373 అయిన పేజీ నెంబర్లను కనుగొనుము.
(సూచన : తెరచిన పేజీల సంఖ్యలు x మరియు x + 1 అనుకొనండి)

సాధన.
తెరచిన పుస్తకంలోని మొదటి పేజీ యొక్క సంఖ్య = x
రెండవ పేజీ సంఖ్య = x + 1 అగును
∴ రెండు పేజీల సంఖ్యల మొత్తము = 373
⇒ x + x + 1 = 373
2x + 1 = 373
2x = 372
∴ x = 186
∴ x + 1 = 186 + 1 = 187
∴ ఆ వరుస పేజీల సంఖ్యలు = 186, 187.

SCERT AP 8th Class Maths Solutions Chapter 2 ఏకచరరాశిలో రేఖీయ సమీకరణాలు Ex 2.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు Exercise 2.1

1. క్రింది సామాన్య సమీకరణాలను సాధించుము.

(i) 6m = 12
సాధన.

(ii) 14p = -42
సాధన.

(iii) – 5y = 30
సాధన.

(iv) – 2x = – 12
సాధన.
– 2x = – 12

(v) 34x = -51
సాధన.

(vi) \(\frac{\mathrm{n}}{7}\) = -3
సాధన.
\(\frac{\mathrm{n}}{7}\) = -3 ⇒ n = -3 × 7 = -21

(vii) \(\frac{2 x}{3}\) = 18
సాధన.

(viii) 3x + 1 = 16
సాధన.
3x + 1 = 16
⇒ 3x = 16 – 1 = 15

(ix) 3p – 7 = 0
సాధన.

(x) 13 – 6n = 7
సాధన.
13 – 6n = 7 ⇒ -6n = 7 – 13

(xi) 200y – 51 = 49
సాధన.
200y – 51 = 49
⇒ 200y = 49 + 51

(xii) 11n + 1 = 1
సాధన.
11n + 1 = 1
⇒ 11n = 1 – 1

(xiii) 7x – 9 = 16
సాధన.
7x – 9 = 16
⇒ 7x = 16 + 9 ⇒ 7x = 25

(xiv) 8x + \(\frac {5}{2}\) = 13
సాధన.
8x + \(\frac {5}{2}\) = 13

(xv) 4x – \(\frac {5}{3}\) = 9
సాధన.
4x – \(\frac {5}{3}\) = 9

(xvi) x + \(\frac {4}{3}\) = 3\(\frac {1}{2}\)
సాధన.

SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు InText Questions

ఇవి చేయండి (పేజీ నెం. 2)

1. కింది సంఖ్యలను పరిశీలించి వాటిని సరైన సంఖ్యా సమితికి ఎదురుగా రాయండి. (ఒక సంఖ్యను ఒకటి కంటే ఎక్కువ సంఖ్యా సమితులకు ఎదురుగా రాయవచ్చు).
1, \(\frac {1}{2}\), -2, 0.5, 4\(\frac {1}{2}\), \(\frac {-33}{7}\), 0, \(\frac {4}{7}\), \(0 . \overline{3}\), 22, – 5, \(\frac {2}{19}\), 0.125.
i) సహజసంఖ్యలు ………, ………, ………, ………, ………,
ii) పూర్ణాంకాలు ………, ………, ………, ………, ………,
iii) పూర్ణ సంఖ్యలు ………, ………, ………, ………, ………, ………, ………, ………
iv) అకరణీయ ………, ………, ………, ………, ………, ………, ………, ………
పైన ఇచ్చిన సంఖ్యలలో ఏదైనా, అకరణీయ సంఖ్యల సమూహంలో రాకుండా మిగిలిపోయినదా ? ఒకవేళ మిగిలితే కారణం తెలపండి.
ప్రతి సహజసంఖ్య, ప్రతీ పూర్ణాంకము మరియు ప్రతీ పూర్ణసంఖ్య, అకరణీయ సంఖ్యయేనా ?
సాధన.

(పేజీ నెం. 6)

2. కింది పట్టికలోని ఖాళీలను పూరించండి.

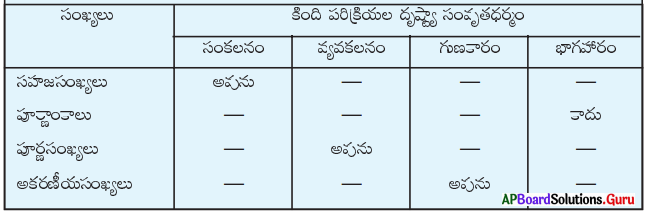
సాధన.

(పేజీ నెం. 9)

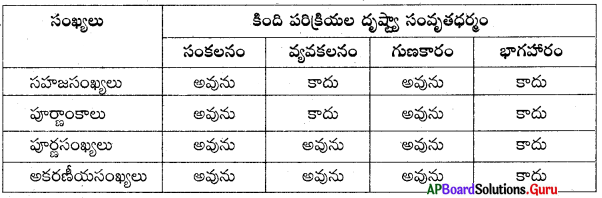
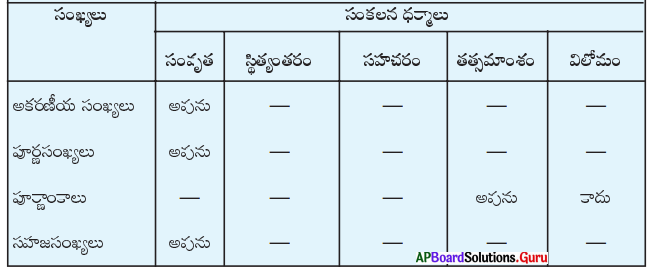
3. కింది పట్టికను పూర్తిచేయండి.

సాధన.

(పేజీ నెం. 13)

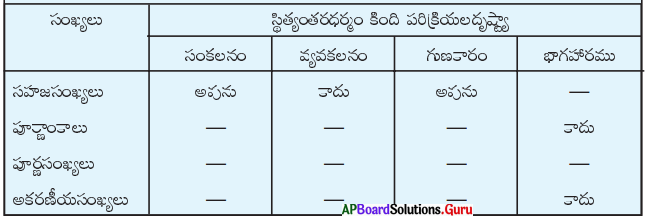
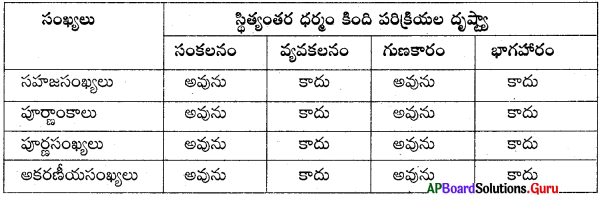
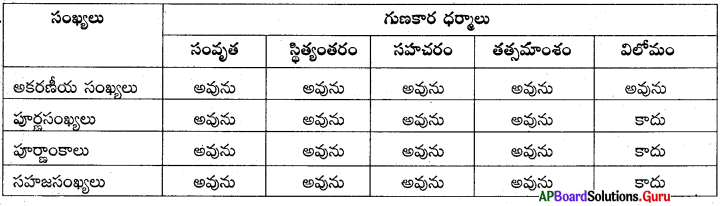
4. కింది పట్టికను పూర్తిచేయండి.

సాధన.

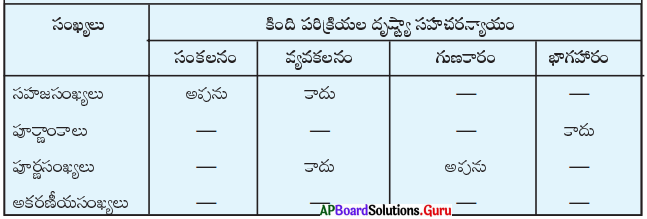
(పేజీ నెం. 16)

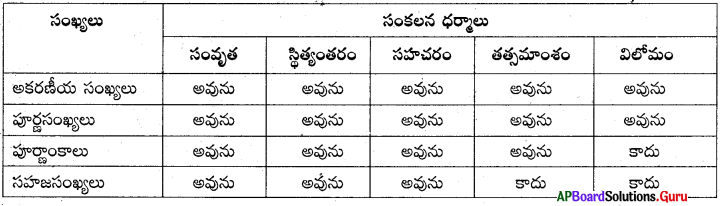
5. కింది పట్టికను పూరించండి.

సాధన.

(పేజీ నెం. 17)

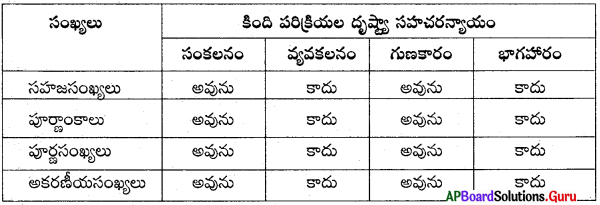
6. కింది పట్టికను పూరించండి.

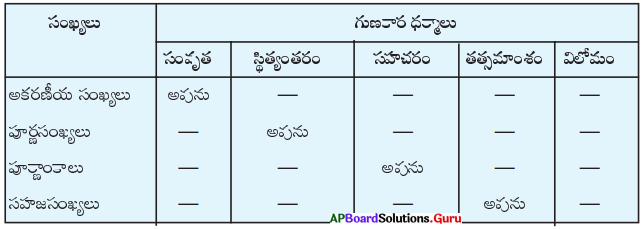
సాధన.

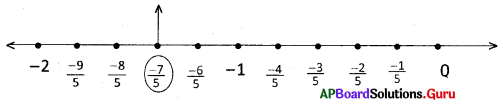
7. –\(\frac {13}{5}\)ను సంఖ్యారేఖపై సూచించండి.
సాధన.
–\(\frac {13}{5}\)ను సంఖ్యారేఖపై చూపించుట.

ప్రయత్నించండి

(పేజీ నెం. 3)

1. హమీద్ : అకరణీయ సంఖ్య అని, 5 కేవలం సహజసంఖ్య మాత్రమే అవుతుందని అన్నాడు. సాక్షి ఈ రెండు సంఖ్యలు అకరణీయ సంఖ్యలు అని చెప్పింది. ఇద్దరి వాదనలో నీవు ఎవరితో ఏకీభవిస్తావు ?
సాధన.
హమీద్ జవాబు సరియైనది కాదు. ఎందుకనగా \(\frac {5}{3}\) ఒక అకరణీయ సంఖ్య. అదేవిధంగా ‘5’ కేవలం సహజసంఖ్య మాత్రమే అవుతుందనటం అసత్యం. ఎందుకనగా ప్రతి సహజసంఖ్య అకరణీయ సంఖ్యయే.
సాక్షి \(\frac {5}{3}\), 5లు రెండూ అకరణీయ సంఖ్యలేనన్న అభిప్రాయం నిజం.
∴ నేను సాక్షి వాదనతో ఏకీభవిస్తాను.

(పేజీ నెం. 3)

2. కింది వాక్యాలను తృప్తిపరిచే ఉదాహరణలు ఇవ్వండి.
i) సహజసంఖ్యలన్నీ పూర్ణాంకాలు అవుతాయి కాని దీని విపర్యయం సత్యం కాదు.
ii) పూర్ణాంకాలన్నీ పూర్ణసంఖ్యలవుతాయి కాని పూర్ణసంఖ్యలన్నీ పూర్ణాంకాలు కావు.
iii) పూర్ణసంఖ్యలన్నీ అకరణీయ సంఖ్యలే కాని అకరణీయ సంఖ్యలన్నీ పూర్ణసంఖ్యలు కావు.
సాధన.
i) ‘0’ సహజసంఖ్య కాదు.
∴ పూర్ణాంకాలన్నీ సహజసంఖ్యలు కావు. (∴ N⊂W)
ii) -2, -3, -4 లు పూర్ణాంకాలు కావు.
∴ పూర్ణ సంఖ్యలన్నీ పూర్ణాంకాలు కావు. (∴ W⊂Z)
iii) \(\frac {2}{3}\), \(\frac {7}{4}\)లు పూర్ణసంఖ్యలు కావు.
∴ అకరణీయ సంఖ్యలన్నీ పూర్ణసంఖ్యలు కావు. (∴ Z⊂Q)

(పేజీ నెం. 6)

3. పూర్ణసంఖ్యల నుంచి సున్నాను మినహాయిస్తే అది భాగహారం దృష్ట్యా సంవృత ధర్మాన్ని పాటిస్తుందా ? ఇదేవిధంగా సహజ సంఖ్యా సమితిలో సున్నా లేదు కాబట్టి సహజసంఖ్యల సమితి భాగహారం దృష్ట్యా సంవృత ధర్మాన్ని పాటిస్తుందా ?
సాధన.
పూర్ణసంఖ్యల నుండి ‘0’ (సున్న)ను తీసివేసిన Z – {0} అగును.
భాగహారం దృష్ట్యా సంవృత, ధర్మం :
ఉదా : – 4 ÷ 2 = – 2 ఒక పూర్ణసంఖ్యయే.
3 ÷ 5 = \(\frac {3}{5}\) ఒక పూర్ణసంఖ్య కాదు.
∴ పూర్ణ సంఖ్యల సమితి నుండి ‘0’ మినహాయించిన [Z- {0}], అది భాగహారం దృష్ట్యా సంవృత ధర్మాన్ని పాటించదు.
సహజసంఖ్యా సమితి పై భాగహారం దృష్ట్యా సంవృత ధర్మం :
ఉదా : 2 ÷ 4 = \(\frac {1}{2}\) ఒక సహజ సంఖ్య కాదు.
∴ భాగహారం దృష్ట్యా సహజసంఖ్యా సమితి సంవృత ధర్మాన్ని పాటించదు.

(పేజీ నెం. 16)

4. విభాగ న్యాయము ఉపయోగించి కింది వానిని కనుగొనండి.
\(\left\{\frac{7}{5} \times\left(\frac{-3}{10}\right)\right\}+\left\{\frac{7}{5} \times \frac{9}{10}\right\}\)
\(\left\{\frac{9}{16} \times 3\right\}+\left\{\frac{9}{16} \times-19\right\}\)
సాధన.
విభాగ న్యాయము .
a × (b + c) = ab + ac

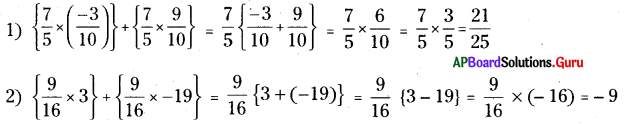
(పేజీ నెం. 22)

5. కింది సంఖ్యారేఖపై ఆంగ్ల అక్షరాలను సూచించే బిందువులు ఏ అకరణీయ సంఖ్యలను సూచిస్తాయి ?

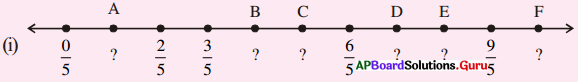
సాధన.
A = \(\frac {1}{5}\), B = \(\frac {4}{5}\), c = \(\frac {5}{5}\) = 1, D = \(\frac {7}{5}\), E = \(\frac {8}{5}\), F = \(\frac {10}{5}\) = 2

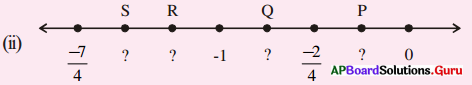
సాధన.
S = \(\frac {-6}{4}\), R = \(\frac {-5}{4}\), Q = \(\frac {-3}{4}\), P = \(\frac {-1}{4}\)

ఆలోచించి, చర్చించి వ్రాయండి

(పేజీ నెం. 15)

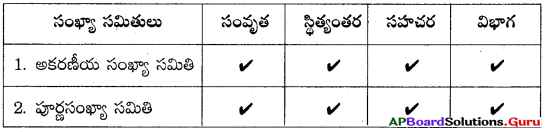
1. సంకలనం దృష్ట్యా అకరణీయ సంఖ్యలు పాటించు ప్రతి ధర్మము పూర్ణసంఖ్యలు కూడా పాటిస్తాయా ? ఏది అవుతుంది? ఏది కాదు ?
సాధన.
సంకలనం దృష్ట్యా అకరణీయ సంఖ్యలు పాటించు ప్రతి ధర్మము పూర్ణసంఖ్యలు పాటించును.

(పేజీ నెం. 15)

2. ఏయే సంఖ్యల గుణకార విలోమాలు అవే సంఖ్యలవుతాయి ? తనకు తానే గుణకార విలోమాలగు సంఖ్యలు ఏవి ?
సాధన.
‘1’ తనకు తానే గుణకార విలోమం అవుతుంది.
1 × = 1
⇒ 1 × 1 = 1
∴ 1 యొక్క గుణకార విలోమం ‘1’ మాత్రమే అగును.

(పేజీ నెం. 15)

3. సున్న (0) యొక్క వ్యుత్తమము నీవు కనుగొనగలవా ? 0 చే గుణించగా లబ్ధం 1 వచ్చే ఏదైనా అకరణీయ సంఖ్య కలదా ?
× 0 = 1 లేదా 0 × = 1
సాధన.
సున్న యొక్క వ్యతమము = \(\frac {1}{0}\) ను కనుగొనలేము.
‘0’ (సున్న)చే గుణింఛగా లబ్దం ‘1’ వచ్చే ఏ అకరణీయ సంఖ్యా లేదు.
∵ 0 × (ఏ సంఖ్య అయిన) = 0 అగును.

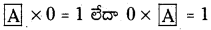
A = ఏ సంఖ్యా లేదు.

(పేజీ నెం. 28)

4. కింది వానిని దశాంశ రూపంలో వ్రాయండి.
i) \(\frac {1}{2}\)
సాధన.
\(\frac {7}{5}\) = 1.4
\(\frac {3}{4}\) = 0.75
\(\frac {23}{10}\) = 2.3
\(\frac {5}{3}\) = 1.66 ……….. = \(1 . \overline{6}\)
\(\frac {17}{6}\) = 2.833 ………= \(2.8 \overline{3}\)
\(\frac {5}{3}\) = 3.142

ii) పై వాటిలో ఏవి అంతమయ్యే దశాంశాలు ? ఏవి అంతం కాని దశాంశాలు ?
సాధన.
పై భిన్నాలలో \(\frac{7}{5}, \frac{3}{4}, \frac{23}{10}\) లు అంతమయ్యే దశాంశాలు.
\(\frac{5}{3}, \frac{17}{6}, \frac{22}{7}\) లు అంతం కాని భిన్నాలు.

iii) పై అకరణీయ సంఖ్యల హారాలను ప్రధాన సంఖ్యల లబ్ధంగా వ్రాయండి.
సాధన.
\(\frac {7}{5}\) లో 5 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 5 × 1
\(\frac {3}{4}\) లో 4 యొక్క ప్రధాన కారణాంకాల లబ్దం = 2 × 2
\(\frac {23}{10}\) లో 10 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 2 × 5
\(\frac {5}{3}\) లో 3 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 3 × 1
\(\frac {17}{6}\) లో 6 యొక్క ప్రధాన కారణాంకాల లబ్దం = 2 × 3
\(\frac {22}{7}\) లో 7 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 7 × 1
(కాని ‘1’ ప్రధాన సంఖ్య కాదు)

iv) కనిష్ఠ రూపంలో ఉండే పై అకరణీయ సంఖ్యల హారానికి 2, 5 తప్ప ఇతర కారణాంకాలు లేకుంటే నీవు ఏం గమనించావు?
సాధన.
ఇచ్చిన కనిష్ఠ రూపంలో ఉండే అకరణీయ సంఖ్యల హారానికి 2, 5 తప్ప ఇతర కారణాంకాలు లేకుంటే ఆ భిన్నాలు “అంతం అయ్యే దశాంశాలు” అగును.

(పేజీ నెం. 31)

5. \(0 . \overline{9}\), \(14 . \overline{5}\) మరియు \(1.2 \overline{4}\) లను అకరణీయసంఖ్యా రూపంలోకి వ్రాయండి. మామూలు సాధనా పద్ధతికి భిన్నంగా ఏదైనా సులభమైన పద్ధతిని నీవు కనుగొనగలవా?
సాధన.
\(0 . \overline{9}\)
x = \(0 . \overline{9}\) = 0.999 ……. —— (1)
(1) లో 9 ఆవర్తితము. దీని యొక్క అవధి 1.
∴ (1)వ సమీకరణాన్ని ఇరువైపులా 10చే గుణించగా
10 × x = 10 × 0.999 ……
10x = 9.999 ……. ——-(2)

మరొక పద్ధతి :
\(0 . \overline{9}\) = 0 + \(\overline{9}\) = 0 + \(\frac {9}{9}\) = 0 + 1 = 1

\(14 . \overline{5}\)
x = \(14 . \overline{5}\)
x = 14.555 …. —– (1)
అవధి ‘1’ కావున (1)వ సమీకరణాన్ని ఇరువైపులా ’10’చే గుణించగా
10 × x = 10 × 14.55 …….
10x = 145.55 ……. —— (2)

మరొక పద్ధతి :

\(1.2 \overline{4}\)
x = \(1.2 \overline{4}\) = 1.2444 ……. —— (1)
ఇచ్చట అవధి ‘1’ కావున (1)వ సమీకరణాన్ని ఇరువైపులా ’10’ చే గుణించగా
⇒ 10 × x = 10 × 1.244 ……
10x = 12.44 ……. —– (2)

మరొక పద్ధతి :

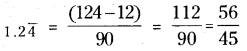
SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు Ex 1.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు Exercise 1.3

ప్రశ్న 1.
కింది వానిని \(\frac{p}{q}\) రూపంలోకి వ్రాయండి.
(i) 0.57 (ii) 0.176 (iii) 1.00001 (iv) 25.125
సాధన.
(i) 0.57 = 0.57 లో దశాంశ స్థానంలో రెండంకెలు ఉన్నాయి. కావున దీనిని 100చే భాగించవలెను.
∴ 0.57 = \(\frac {57}{100}\)
(Note : పాయింట్ తరువాత ఎన్ని అంకేలుంటే హారంలో అన్ని ‘సున్నా’లుండాలి.)
(ii) 0.176 = \(\frac {176}{1000}\)
(iii) 1.00001 = \(\frac {100001}{100000}\)
(iv) 25.125 = \(\frac {25125}{1000}\)

ప్రశ్న 2.
ఈ కింది ఆవృత దశాంశాలను అకరణీయ సంఖ్యా రూపంలో వ్యక్తపరచండి. (\(\frac{p}{q}\)).
(i) \(0 . \overline{9}\) (ii) \(0 . \overline{57}\) (iii) \(0.7 \overline{29}\) (iv) \(12.2 \overline{8}\)
సాధన.
(i) \(0 . \overline{9}\)
x = 0.9 = 0.999 …….
⇒ x = 0.999 ……. ——- (1) లో 9 ఆవర్తితము.
దీని యొక్క అవధి 1.
∴ (1)వ సమీకరణాన్ని ఇరువైపులా 10చే గుణించగా
10 × x = 10 × 0.999 ……
10x = 9.999 …… —— (2)

x = \(\frac {9}{9}\) = 1
∴ \(0 . \overline{9}\) = 1

మరొక పద్ధతి :
\(0 . \overline{9}\) = 0 + \(\overline{9}\)
= 0 + \(\frac {9}{9}\)
= 0 + 1 = 1

(ii) \(0 . \overline{57}\)
x = \(0 . \overline{57}\) = 0.5757 …….. —– (1)
ఇచ్చట అవధి 2 కావునా ఇరువైపులా ‘100’చే గుణించ వలెను.
⇒ 100 × x = 100 × 0.5757 …….
100x = 57.57 …… —– (2)

∴ x = \(\frac {57}{99}\) లేదా x = \(\frac {19}{33}\)

(iii) \(0.7 \overline{29}\)
x = \(0.7 \overline{29}\) = 0.72929 ….. —– (1)
ఇచ్చట అవధి 2 కావునా ఇరువైపులా (1)వ సమీకరణాన్ని 100చే గుణించగా
⇒ 100 × x = 100 × 0.72929 ……..
⇒ 100x = 72.9929 …… —– (2)

99x = 72.2
x = \(\frac {72.2}{99}\) = \(\frac {722}{990}\)
∴ x = \(\frac {361}{495}\)

(iv) \(12.2 \overline{8}\)
x = 12.288 …… …………..(1)
ఇచ్చట అవధి ‘1’ కావునా ఇరువైపులా ’10’చే గుణించగా
⇒ 10 × x = (12.288) × 10 ……
10x = 122.888 …… ……… (2)

3. కింద ఇచ్చిన విలువలకు (x + y) – (x – y) ను లెక్కించండి.
(i) x = \(\frac {5}{2}\), y = –\(\frac {3}{4}\)
(ii) x = \(\frac {1}{4}\), y = \(\frac {3}{2}\)
సాధన.
(i) x = \(\frac {5}{2}\), y = –\(\frac {3}{4}\) అయిన

(ii) x = \(\frac {1}{4}\), y = \(\frac {3}{2}\) అయిన

ప్రశ్న 4.
–\(\frac {13}{5}\) మరియు \(\frac {12}{7}\) ల మొత్తాన్ని –\(\frac {13}{7}\) మరియు –\(\frac {1}{2}\) ల లభించే భాగించండి.
సాధన.
–\(\frac {13}{5}\) మరియు \(\frac {12}{7}\) ల మొత్తం

ప్రశ్న 5.
ఒక సంఖ్య యొక్క \(\frac {2}{5}\) వ భాగం ఆ సంఖ్య యొక్క \(\frac {1}{7}\) వ భాగం కంటే 36 ఎక్కువ అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య ‘x’ అనుకొనుము.
‘x’ యొక్క \(\frac {2}{5}\) వ భాగం = \(\frac {2}{5}\) × x = \(\frac{2 x}{5}\)
x యొక్క \(\frac {1}{7}\)వ భాగం = \(\frac {1}{7}\) × x = \(\frac{x}{7}\)
∴ లెక్క ప్రకారం

ప్రశ్న 6.
11 మీ. పొడవు గల తాడు నుండి 2\(\frac {3}{5}\) మీ. మరియు 3\(\frac {3}{10}\)మీ. పొడవులు గల రెండు ముక్కలు కత్తిరించగా మిగిలిన ముక్క పొడవు ఎంత ?
సాధన.
మిగిలిన తాడు ముక్క పొడవు

ప్రశ్న 7.
7\(\frac {2}{3}\) మీటర్ల పొడవు గల ఒక గుడ్డ ఖరీదు ₹12\(\frac {3}{4}\) అయిన ఒక మీటరు గుడ్డ ఖరీదు ఎంత ?
సాధన.
7\(\frac {2}{3}\) మీ॥ల (\(\frac {23}{3}\)మీ.) పొడవు గల గుడ్డ ఖరీదు
= ₹12\(\frac {3}{4}\) = ₹\(\frac {51}{4}\)
∴ 1 మీ. గుడ్డ ఖరీదు = \(\frac{51}{4} \div \frac{23}{3}\)
= \(\frac {51}{4}\) × \(\frac {3}{23}\)
= \(\frac {153}{92}\)
= ₹1.66

ప్రశ్న 8.
18\(\frac {3}{15}\) మీ. పొడవు మరియు 8\(\frac {2}{3}\)మీ. వెడల్పు గల ఒక దీర్ఘ చతురస్రాకార పార్క్ వైశాల్యం కనుగొనండి.
సాధన.
దీర్ఘచతురస్రాకార పార్క్
పొడవు = 18\(\frac {3}{15}\) మీ. = \(\frac {93}{5}\) మీ.
వెడల్పు = 8\(\frac {2}{3}\) మీ. = \(\frac {26}{3}\)మీ.
∴ దీర్ఘచతురస్రాకార పార్క్ వైశాల్యం (A) = l × b

ప్రశ్న 9.
–\(\frac {33}{16}\) ను ఏ సంఖ్యచే భాగించగా –\(\frac {11}{4}\) వస్తుంది ?
సాధన.
భాగించవలసిన సంఖ్య ‘x’ అనుకొనుము.

ప్రశ్న 10.
64 మీటర్ల పొడవు గల ఒక బట్ట నుంచి సమాన పరిమాణం గల 36 ప్యాంటులు తయారుచేసిన ఒక్కొక్క , ప్యాంటు తయారుచేయుటకు ఎంత పొడవు గల బట్ట అవసరము ?
సాధన.
64 మీటర్ల పొడవు గల ఒక బట్ట నుంచి సమాన పరిమాణం గల 36 ప్యాంట్లు తయారుచేసిన ఒక్కొక్క ప్యాంటు తయారుచేయుటకు అవసరం అగు బట్ట పొడవు = 64 ÷ 36

ప్రశ్న 11.
ఆవర్తిత దశాంశ సంఖ్య 10.363636… ను \(\frac{p}{q}\) రూపంలో రాసిన p + q విలువ కనుగొనండి.
సాధన.
x = 10.363636 … ………………. (1)
ఇచ్చట అవధి 2.
(1)వ సమీకరణాన్ని ఇరువైపులా 100చే భాగించగా
⇒ 100 × x = 100 × 10.363636 …..
100x = 1036.36 … ……………… (2)

SCERT AP 8th Class Maths Solutions Chapter 1 అకరణీయ సంఖ్యలు Ex 1.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson అకరణీయ సంఖ్యలు Exercise 1.2

ప్రశ్న 1.
కింది అకరణీయ సంఖ్యలను సంఖ్యారేఖపై చూపుము.
(i) \(\frac {9}{7}\)
(ii) –\(\frac {7}{5}\)
సాధన.
(i) \(\frac {9}{7}\)

(ii) –\(\frac {7}{5}\)

ప్రశ్న 2.
\(-\frac{2}{13}, \frac{5}{13}, \frac{-9}{13}\) లను ఒకే సంఖ్యారేఖపై సూచించండి.
సాధన.

ప్రశ్న 3.
\(\frac {5}{6}\) కంటే చిన్నవయిన ఐదు అకరణీయ సంఖ్యలను వ్రాయండి.
సాధన.
\(\frac {5}{6}\) కంటే చిన్నవైన అకరణీయ సంఖ్యలు
\(\left\{\frac{4}{6}, \frac{3}{6}, \frac{2}{6}, \frac{1}{6}, \frac{0}{6}, \frac{-1}{6}, \frac{-2}{6}, \ldots \ldots\right\}\)

ప్రశ్న 4.
-1 మరియు 2 ల మధ్య గల 12 అకరణీయ సంఖ్యలను కనుగొనండి.
సాధన.
-1 = \(\frac {-12}{12}\) మరియు 2 = \(\frac{2 \times 12}{12}\) = \(\frac {24}{12}\)
∴ -1 మరియు 2ల మధ్య గల అకరణీయ సంఖ్యలు

నుండి ఏవేని 12 అకరణీయ సంఖ్యలు తీసుకొన వచ్చును.

ప్రశ్న 5.
\(\frac {2}{3}\) మరియు \(\frac {3}{4}\) ల మధ్య ఒక అకరణీయ సంఖ్యను కనుగొనుము.
(సూచన : ఇచ్చిన అకరణీయ సంఖ్యలను సజాతి భిన్నాలుగా మార్చండి.)
సాధన.

ప్రశ్న 6.
\(\frac {-3}{4}\) మరియు \(\frac {5}{6}\) ల మధ్య పది అకరణీయ సంఖ్యలు కనుగొనండి.
సాధన.
\(\frac {-3}{4}\) మరియు \(\frac {5}{6}\)


\(\frac {-9}{12}\), \(\frac {10}{12}\) ల మధ్య ఏవైనా 10 అకరణీయ సంఖ్యలు ఎన్నుకోవచ్చును.