Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 7 Definite Integrals to solve questions creatively.
Intermediate 2nd Year Maths 2B Definite Integrals Formulas
→ If f is a function integrable over an interval [a, b] and F is a primitive offon [a, b] then
\(\int_{a}^{b}\)f(x)dx = F(b) – F(a)
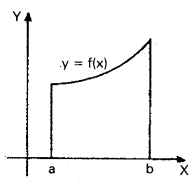
→ If a < b be real numbers and y = f(x) denote a curve in the plane as shown in figure. Then the definite integral \(\int_{a}^{b}\) f(x) dx is equal to the area of the region bounded by the curve y = f(x), the ordinates x = a, x = b and the portion of X-axis.
→ \(\int_{a}^{b}\)f(x) dx = — \(\int_{b}^{a}\)f(x) dx
→ \(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\)f(x) dx ; a < c < b
→ \(\int_{a}^{b}\)f[g(x)] g’ (x) dx = \(\int_{g(a)}^{g(b)}\)f(x)dx
→ \(\int_{0}^{a}\)f(x)dx = \(\int_{0}^{a}\)f(a-x)dx
→ \(\int_{0}^{2 a}\)f(x)dx =2\(\int_{0}^{a}\)f(x)dx , if f(2a-x) = f(x)
= 0, if f(2a – x) = -f(x)
![]()
→ \(\int_{-a}^{a}\)f(x)dx = 2\(\int_{0}^{a}\)f(x)dx if f is even
= 0, if f is odd
→ Let f(x) be a function defined on [a, b]. If ∫ f(x)dx = F(x), then F(b) – F(a) is called the definite integral of f(x) over [a, b]. It is denoted by \(\int_{a}^{b}\) f(x)dx. The real number ‘a’ is called the lower limit and the real number ‘b’ is called the upper limit.
This is known as fundamental theorem of integral calculus.
Geometrical Interpretation of Definite Integral:
If f(x)>0 for all x in [a, b] then \(\int_{a}^{b}\) f (x)dx is numerically equal to the area bounded by the curve y =f(x), the x-axis and the lines x = a and x = b i.e., \(\int_{a}^{b}\) f (x) dx
Properties of Definite Integrals:
- \(\int_{a}^{b}\)f (x)dx = \(\int_{a}^{b}\)f(t)dt i.e., definite integral is independent of its variable.
- \(\int_{a}^{b}\)f(x) dx = – \(\int_{b}^{a}\)f(x) dx
- \(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\)f(x) dx ; a < c < b
- \(\int_{a}^{b}\)f[g(x)] g’ (x) dx = \(\int_{g(a)}^{g(b)}\)f(x)dx
- \(\int_{0}^{a}\)f(x)dx = \(\int_{0}^{a}\)f(a-x)dx
- \(\int_{0}^{2 a}\)f(x)dx =2\(\int_{0}^{a}\)f(x)dx , if f(2a-x) = f(x)
= 0, if f(2a – x) = -f(x) - \(\int_{-a}^{a}\)f(x)dx = 2\(\int_{0}^{a}\)f(x)dx if f is even
= 0, if f is odd
Theorem:
If f(x) is an integrable function on [a, b] and g(x) is derivable on [a, b] then
\(\int_{a}^{b}\)(fog)(x)g'(x)dx = \(\int_{g(a)}^{g(b)}\)f(x) dx \(\int_{a}^{b}\)(fog)(x)g'(x)dx = \(\int_{g(a)}^{g(b)}\)f(x) dx
Areas Under Curves:
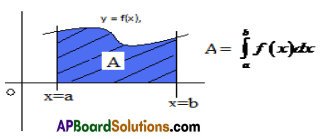
1. Let f be a continuous curve over [a, b]. If f(x) ≥ o in [a, b], then the area of the region bounded by y = f(x), x-axis and the lines x=a and x=b is given by \(\int_{a}^{b}\)f(x)dx.
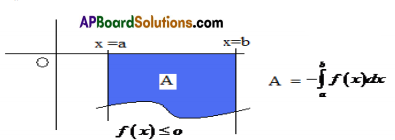
2. Let f be a continuous curve over [a, b]. If f (x) ≤ o in [a, b], then the area of the region bounded by y = f(x), x-axis and the lines x=a and x=b is given by –\(\int_{a}^{b}\) f (x)dx.
3. Let f be a continuous curve over [a,b]. If f (x) ≥ o in [a, c] and f (x) ≤ o in [c, b] where a < c < b. Then the area of the region bounded by the curve y = f(x), the x-axis and the lines x=a and x=b is given by \(\int_{a}^{c}\)f (x )dx – \(\int_{c}^{b}\)f (x )dx
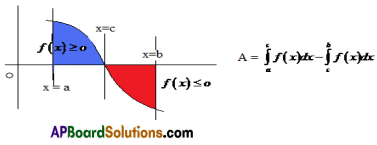
4. Let f(x) and g(x) be two continuous functions over [a, b]. Then the area of the region bounded by the curves y = f (x), y = g (x) and the lines x = a, x=b is given by |\(\int_{a}^{b}\)f(x)dx – \(\int_{a}^{b}\)g(x)dx|
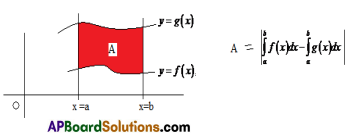
![]()
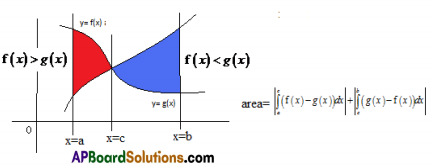
5. Let f(x) and g(x) be two continuous functions over [a, b] and c ∈ (a, b). If f (x) > g (x) in (a, c) and f (x) < g (x) in (c, b) then the area of the region bounded by the curves y = f(x) and y= g(x) and the lines x=a, x=b is given by |\(\int_{a}^{c}\)(f (x) – g (x ))dx| + |\(\int_{c}^{b}\)(g(x)-f (x))dx|
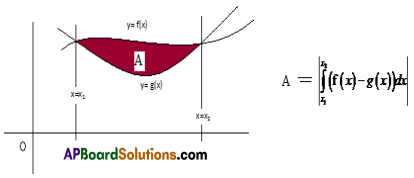
6. let f(x) and g(x) be two continuous functions over [a, bi and these two curves are intersecting at X =x1 and x = x2 where x1, x 2, ∈ (a,b) then the area of the region bounded by the curves y= f(x) and y = g(x) and the lines x = x1, x = x2 is given by |\(\int_{x_{1}}^{x_{2}}\)(f(x) – g(x))dx|
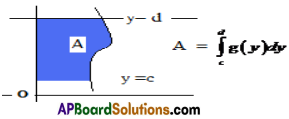
Note: The area of the region bounded by x =g(y) where g is non negative continuous function in [c, d], the y axis and the lines y = c and y = d is given by \(\int_{c}^{d}\)g(y)dy .