AP 10th Class Maths Important Questions Chapter 3 బహుపదులు

These AP 10th Class Maths Chapter Wise Important Questions 3rd Lesson బహుపదులు will help students prepare well for the exams.

AP Board 10th Class Maths 3rd Lesson Important Questions and Answers బహుపదులు

ప్రశ్న 1.
p(x) = x² – 5x – 6 అయిన p(3) ను కనుగొనుము.
సాధన.
p(x) = x² – 5x – 6 అయిన
P(3) = 3² – 5(3) – 6
= 9 – 15 – 6
= 9 – 21 = 0
∴ p(3) = – 12 అగును.

ప్రశ్న 2.
రెండు వేర్వేరు బహుపదులను రాసి, ప్రతి దానికి రెండు ప్రశ్నలు చొప్పున రూపొందించండి.
సాధన.
(1) p(x) = x² – 4
i) p(x) పరిమాణము ఎంత ?
ii) p(x) యొక్క శూన్యాల మొత్తం కనుగొనుము.

(2) p(x) = 2x + 3
i) p(x) లోని పదాల సంఖ్య ఎంత ?
ii) p(x) యొక్క శూన్య విలువను కనుగొనండి.

ప్రశ్న 3.
2x⁴ + x + k బహుపదిలో ఓ యొక్క ఏ విలువకు 3 బహుపది శూన్య విలువగును?
సాధన.
p(x) = 2x² + x + k బహుపదికి 3 ఒక శూన్యము కనుక
p(3) = 0.
∴ p(3) = 2(3)² + 3 + k = 0
⇒ 21 + k = 0
⇒ k = – 21.

ప్రశ్న 4.
x-y = 0 యొక్క రఫ్ గ్రాఫ్ గీయుము.
సాధన.

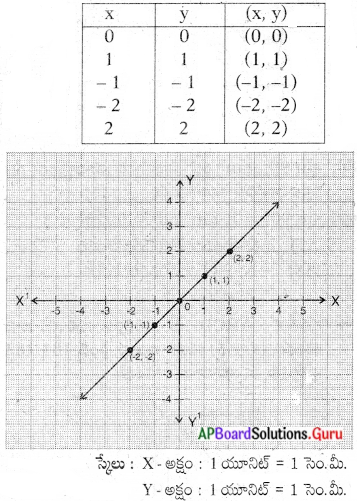
ప్రశ్న 5.
7×3 – 3×2 + 5x – 2 ని x + 2 చే భాగించగా శేషం కనుగొనండి.
సాధన.

∴ శేషం = – 80.

ప్రశ్న 6.
p(y) = y³ – 1 అయిన 1, – 1 లు p(y) కు శూన్యాలు అవుతాయో ? లేదో ? సరిచూడండి.
సాధన.
p(y) = y³ – 1
p(1) = 1³ – 1 = 1 – 1 = 0 :
∴ p(y) కు ‘1’ శూన్యం.
p(- 1) = (- 1)³ – 1
= – 1 – 1 = – 2
∴ p(y) కు ‘- 1’ శూన్యం కాదు.

ప్రశ్న 7.
5x² – 4 – 8x వర్గ బహుపది యొక్క శూన్యాలను కనుగొని, శూన్యాలకు, బహుపది గుణకాలకు మధ్య గల సంబంధాన్ని సరిచూడుము.
సాధన.
ఇచ్చిన బహుపది = 5x² – 4 – 8x
= 5x² – 8x – 4
= 5x² – 10x + 2x – 4
= 5x(x – 2) + 2(x – 2)
= (x – 2) (5x + 2)
శూన్యాలు కనుగొనుటకు, (x – 2) (5x + 2) = 0
⇒ x – 2 = 0 లేదా 5x + 2 = 0
⇒ x = 2 లేదా x = – \(\frac{2}{5}\)
శూన్యాల మొత్తం = 2 + (- \(\frac{2}{5}\)) = (\(\frac{8}{5}\))
= -(-\(\frac{8}{5}\))
= – x గుణకం / x² గుణకం
శూన్యాల లబ్దం = 2(- \(\frac{2}{5}\))
= \(\frac{-4}{5}\) = స్థిరపగం / x² గుణకం.

ప్రశ్న 8.
\(\frac{2}{3}\) మరియు 2 లు శూన్యాలుగా గల వర్గ బహుపదినీ కనుగొనండి.
సాధన.
α, β లు శూన్యాలుగా కలిగిన వర్గ బహుపది
ax² + bx + c, a ≠ 0 అనుకోండి.
ఇక్కడ, α = \(\frac{2}{3}\) మరియు β = 2.
శూన్యాల మొత్తం = α + β = \(\frac{2}{3}\)(2) = \(\frac{4}{3}\)
∴ శూన్యాల లబ్ధం = αβ = 1 (2) = 2
∴ కావున, వర్గ బహుపది = [x² – (α + β)x + αβ]
= [x² – \(\frac{8}{3}\)x + \(\frac{4}{3}\)]
∴ కావలసిన వర్గ బహుపది 3x² – 8x + 4.

ప్రశ్న 9.
x² – x – 30 వర్గ బహుపది యొక్క శూన్యాలను కనుగొని, బహుపది గుణకాలకు, శూన్యాలకు గల సంబంధాన్ని సరిచూడండి.
సాధన.
ఇచ్చిన బహుపది x² – x – 30
శూన్యాలు కనుగొనుటకు x² – x – 30 = 0 అనుకొనుము.
⇒ x² – x – 30 = 0
⇒ x² – 6x + 5x – 30 = 0
⇒ x(x – 6) + 5(x – 6) = 0
⇒ (x – 6) (x + 5) = 0
⇒ x – 6 = 0
⇒ x = 6
∴ a = 6, P = – 5
శూన్యాల మొత్తం = α + β = \(-\frac{b}{a}\)
⇒ 6 – 5 = 1
⇒ 1 = 1
శూన్యాల లబ్దం = αβ = 6(- 5) = \(\frac{c}{a}\)
= – 30 = \(\frac{-30}{1}\).

ప్రశ్న 10.
శూన్యాల మొత్తం – 3 మరియు శూన్యాల వర్గాల మొత్తం 17 గా కలిగిన వర్గ బహుపదిని కనుగొనండి.
సాధన.
శూన్యాల మొత్తం = α + β = – 3
శూన్యాల వర్గాల మొత్తు = 17
(α + β)² = α² + β² + 2αβ
(- 3)² = 17 + 2αβ
2αβ = 9 – 17 = – 8.
∴ వర్గ బహుపది = x² – (α + β)x + αβ
= x² – (- 3) x + (- 4)
= x² + 3x – 4

ప్రశ్న 11.
p మరియు q లు బహుపది 3x² – 5x + 2 యొక్క శూన్యములైన, \(\frac{1}{p}\) మరియు \(\frac{1}{q}\) లు శూన్యాలుగా గల బహుపదిని ‘x’ లో వ్రాయుము.
సాధన.
p, q లు శూన్యాలుగా కలిగిన వర్గ బహుపది 3x² – 5x + 2.
శూన్యాల మొత్తం = p + q = \(\frac{-(-5)}{3}=\frac{5}{3}\) ………. (1)
శూన్యాల లబ్దం = pq = \(\frac{2}{3}\) ……………. (2)
ఇపుడు, \(\frac{1}{p}\) మరియు \(\frac{1}{q}\)

బహుపదిని కనుగొనుట :
శూన్యాల మొత్తం = \(\frac{1}{p}+\frac{1}{q}=\frac{p+q}{p q}=\frac{\frac{5}{3}}{\frac{2}{3}}=\frac{5}{2}\)
శూన్యాల లబ్దం = \(\frac{1}{p} \times \frac{1}{q}=\frac{1}{p q}=\frac{1}{\frac{2}{3}}=\frac{3}{2}\)
కావున, వర్గ బహుపది x² – (\(\frac{5}{2}\)) x + \(\frac{3}{2}\)
= (2x² – 5x + 3)
∴ కావలసిన వర్గ బహుపది 2x² – 5x + 3.

ప్రశ్న 12.
x² – 3x – 4 వర్గ బహుపదిని గ్రాఫు ద్వారా సాధించండి.
సాధన.
y = x² – 3x – 4 అనుకొనుము y = x² – 3x – 4 గీయుటకు బిందువులను కనుగొనుము.
y = x² – 3x – 4

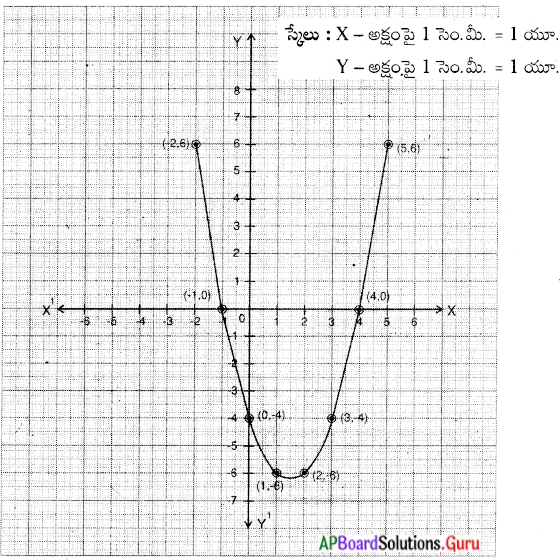
ప్రశ్న 13.
బహుపదులు 4x² + 4x – 3 అనే బహుపదికి రేఖాచిత్రమును గీసి, దాని ద్వారా శూన్యాలను కనుగొనుము.
సాధన.

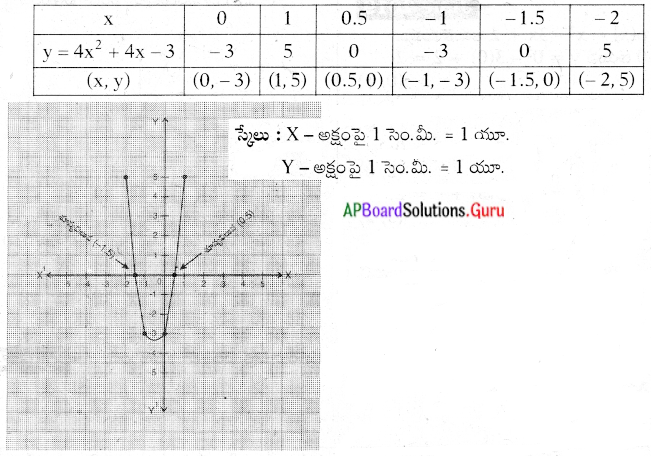
పై వక్రం X – అక్షంను (0.5, 0) మరియు (= 1.5, 0) బిందువుల వద్ద ఖండిస్తున్నది.
కావున పై బహుపది y = 4x² + 4x – 3 యొక్క శూన్యాలు 0.5 మరియు – 1.5.

ప్రశ్న 14.
p(x) = x² – x – 2 వర్గ బహుపదికి గ్రాఫ్ గీసి, శూన్యాలను కనుగొనండి.
సాధన.
y = x² – x – 2 అనుకొనుము.

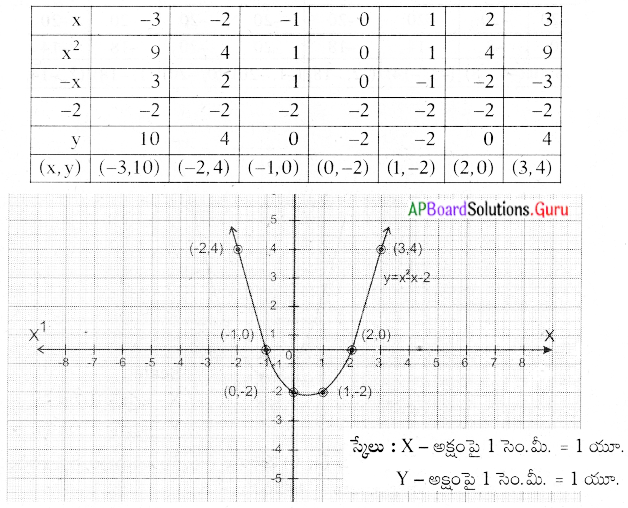
∴ బహుపది శూన్యాలు 2, – 1.

ప్రశ్న 15.
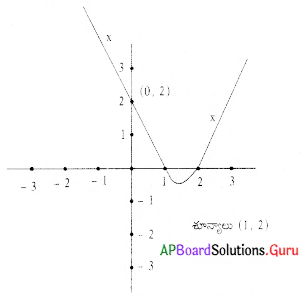
p(x) = x² – 3x + 2 వర్గ బహుపది యొక్క రేఖా చిత్రాన్ని గీసి, శూన్యాలను కనుక్కోండి.
సాధన.
y = p(x) = x² – 3x + 2 అనుకొనుము.
x = 0 అయిన y = 0² – 3(0) + 2 = 2; (0, 2)
x = 1 అయిన y = 1² – 3(1) + 2 = 0; (1, 0)
x = 2 అయిన y = 2² – 3(2) + 2 = 0; (2, 0)
x = 3 అయిన y = 3² – 3(3) + 2 = 2; (3, 2)
x = – 1 అయిన y = (- 1)² – 3(-1) + 2
= 1 + 3 + 2 = 6 అయిన (- 1, 6)
x = – 2 అయిన y = (- 2)² – 3(- 2) + 2
= 4 + 6 + 2 = 12 అయిన (- 2, 12)
అనగా పై వర్గ బహుపదిఈ (0, 2), (1, 0), (2, 0), (3, 2), (- 1, 6), (-2, 12) బిందువుల గుండా పోతుంది.

ప్రశ్న 16.
p(x) = x² + x – 20 వర్గ బహుపది యొక్క శూన్యాలను రేఖాచిత్ర పద్ధతిలో కనుక్కోండి.
సాధన.
y = x² + x – 20 అనుకొనుము.
p(x) = x² + x – 20
p(x) కు విలువలు :

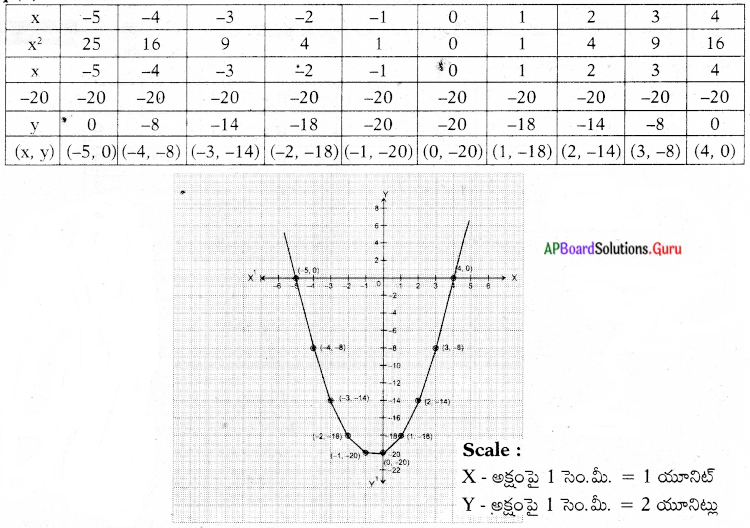
ఫలితము : గ్రాఫును పరిశీలించగా X – అక్షము (4, 0) మరియు (- 5, 0) బిందువుల వద్ద ఖండించును.
∴ ఇచ్చిన బహుపది శూన్యవిలువలు = 4 మరియు – 5.