Students can go through AP Board 6th Class Maths Notes Chapter 5 Fractions and Decimals to understand and remember the concepts easily.
AP State Board Syllabus 6th Class Maths Notes Chapter 5 Fractions and Decimals
→ Fraction: A fraction is a numerical representation of apart of a whole. The whole may be a single object or a group of objects.
Eg: \(\frac{4}{7}\).
The fraction \(\frac{4}{7}\) represents four out of seven.
In the fraction \(\frac{4}{7}\), 4 is called the numerator and 7 is called the denominator.
→ Proper fraction: A fraction in which the numerator is less than its denominator is called a proper fraction.
Eg: \(\frac{1}{7}\), \(\frac{2}{5}\), \(\frac{3}{11}\), …..
All proper fractions are less than 1.
![]()
→ Improper fraction: A fraction in which the numerator is greater than its denominator is called an improper fraction.
Eg: \(\frac{5}{11}\), \(\frac{4}{7}\), \(\frac{2}{3}\),….
All improper fractions are greater than or equal to 1.
→ Mixed fraction: A mixed fraction is a combination of a whole number and a proper fraction.
Fraction in lowest terms: A fraction is said to be in its lowest terms if the numerator and the denominator have no factors in common other than 1.
Eg: \(\frac{2}{11}\), \(\frac{3}{7}\), \(\frac{18}{25}\),……
Equivalent fractions: Two fractions are said to be equivalent if they have same numerators and same denominators respectively when expressed in their lowest terms.
Eg : \(\frac{2}{5}\) & \(\frac{8}{20}\)
Equivalent fractions have the same value.
→ Like fractions:
Fractions with the same denominators are called like fractions
Eg: \(\frac{3}{13}\), \(\frac{4}{13}\), \(\frac{7}{13}\), \(\frac{21}{13}\), ….
→ Un-like fractions:
Fractions with different denominators are called like fractions.
Eg: \(\frac{7}{11}\), \(\frac{3}{5}\), \(\frac{9}{17}\), ….
→ Comparison of fractions:
- Out of two fractions with the same denominators (like fractions), the fraction with the smallest numerator is smaller than the other.
- Similarly out of two fractions with the same denominators (like fractions), the fraction with the greatest numerator is greater than the other.
Eg: \(\frac{2}{11}\) < \(\frac{5}{11}\) \(\frac{9}{17}\) > \(\frac{4}{17}\) - Out of two given fractions with the same numerator, the fraction with smaller denominator is greater than the other.
- Similarly out of two given fractions with the same numerator, the fraction with greater denominator is smaller than the other.
Eg: \(\frac{11}{2}\) > \(\frac{11}{5}\) \(\frac{13}{8}\) < \(\frac{13}{11}\) - To compare unlike fractions, convert them in to like fractions with L.C.M. as the same denominators, and then compare the like fractions.
Eg: \(\frac{2}{3}\) and \(\frac{4}{5}\).
LCM of 2, 5 is 15
\(\frac{2}{3}\) = \(\frac{10}{15}\) \(\frac{4}{5}\) = \(\frac{12}{15}\)
Now \(\frac{10}{15}\) < \(\frac{12}{15}\) there by \(\frac{2}{3}\) < \(\frac{4}{5}\)
![]()
→ Addition and subtraction of like fractions:
- To add like fractions we add their numerators while retaining the common denominator. Eg: \(\frac{5}{7}\) + \(\frac{2}{7}\) = 5 + \(\frac{2}{7}\) = \(\frac{7}{7}\)
- To subtract like fractions we subtract their numerators while retaining the common denominator.
Eg: \(\frac{6}{13}\) – \(\frac{2}{13}\) = 6 – \(\frac{2}{13}\) = \(\frac{4}{13}\)
→ Addition and subtraction of un-like fractions:
- Convert the given unlike fractions in to like fractions, (denominator = LCM of given denominators)
- Now add or subtract as we do in case of like fractions.
- To multiply a fraction with a whole number, first multiply the numerator of the fraction by the whole number while keeping the denominator the same.
Eg: \(\frac{3}{4}\) × 5 = 3 × \(\frac{5}{4}\) = \(\frac{15}{4}\)
8 × \(\frac{2}{3}\) = 8 × \(\frac{2}{3}\) = \(\frac{16}{3}\)
→ Multiplication of two fractions = product of numerators/product of denominators
Eg: \(\frac{5}{6}\) × \(\frac{4}{9}\) = 5 × \(\frac{4}{6}\) × 9 = \(\frac{20}{54}\)
- The product of any two proper fractions is always less than each of its fraction.
Eg: \(\frac{1}{5}\) × \(\frac{2}{7}\) = \(\frac{2}{35}\), \(\frac{2}{35}\) < \(\frac{1}{5}\) & \(\frac{2}{35}\) < \(\frac{2}{7}\) - The product of any two improper fractions is always greater than each of its fraction.
Eg: \(\frac{7}{3}\) × \(\frac{5}{2}\) = \(\frac{35}{6}\) \(\frac{7}{3}\) < \(\frac{35}{6}\) \(\frac{5}{2}\) < \(\frac{35}{6}\) - The product of a proper fraction and an improper fraction is always greater than its proper fraction and less than its improper fraction.
Eg: \(\frac{2}{5}\) × \(\frac{7}{4}\) = \(\frac{14}{20}\) \(\frac{2}{5}\) < \(\frac{14}{20}\) < \(\frac{7}{4}\)
→ Reciprocal of a fraction: A fraction obtained by interchanging the numerator and the denominator of a given fraction is called its reciprocal fraction.
Eg: Reciprocal of \(\frac{3}{4}\) is \(\frac{4}{3}\)
\(\frac{1}{a}\) of b means \(\frac{1}{a}\) × b = \(\frac{b}{a}\)
→ Division of a whole number by a fraction: To divide a whole number by a fraction we multiply the given whole number by the reciprocal of the given fraction.
Eg: 5 ÷ \(\frac{3}{4}\) = 5 × \(\frac{20}{5}\) = \(\frac{4}{5}\)
- Any two non-zero numbers whose product is equal to 1 are called reciprocals to each other.
Eg: \(\frac{3}{7}\) and \(\frac{7}{3}\) are reciprocals to each other. - To divide a whole number by a mixed fraction, first convert the mixed fraction into improper fraction and then multiply the whole number with the reciprocal of the improper fraction.
Eg: 7 ÷ 3\(\frac{2}{5}\) = 7 ÷ \(\frac{17}{5}\) = 7 × \(\frac{5}{17}\) = \(\frac{35}{17}\)
![]()
→ Division of a fraction by a whole number:
- To divide a fraction by a whole number we multiply the given fraction by the reciprocal of the given whole number.
Eg: \(\frac{5}{4}\) ÷ 3 = \(\frac{5}{4}\) × \(\frac{1}{3}\) = \(\frac{5}{12}\) - To divide a mixed fraction by a whole number, first convert the mixed fraction into an improper fraction and then multiply the improper fraction by the reciprocal of whole number.
Eg : 4\(\frac{3}{4}\) ÷ 8 = \(\frac{19}{4}\) × \(\frac{1}{8}\) = \(\frac{19}{32}\)
→ Division of a fraction by another fraction: To divide a fraction by another fraction, we multiply the first fraction with the reciprocal of the second fraction.
E.g: \(\frac{3}{5}\) ÷ \(\frac{7}{11}\) = \(\frac{3}{5}\) × \(\frac{11}{7}\) = \(\frac{33}{35}\)
→ Decimal numbers or Decimal fractions: A decimal is a way of expressing a fraction.
The fraction \(\frac{1}{10}\) is written as 0.1 in decimal form.

Examples for decimal numbers: 0.7, 0.4, 0.23, ..etc The decimal number 0.7 is read as zero point seven.
The decimal number 5.8 is read as five point eight.
The dot or the point between the two digits is called the decimal point.
The number of digits after decimal point is called the number of decimal places. Decimal places of 5.247 is 3.
The decimal point separates a decimal number into two parts. The number on its left as integer part and the digits on its right as decimal part.
The decimal part of a decimal number is always less than 1. As we move from left to right each decimal place decreases by tenth of its previous value.
The decimal places after the decimal point are (\(\frac{1}{10}\)-tenths), (\(\frac{1}{100}\)-hundreths), (\(\frac{1}{1000}\)-thousandths) and so on.
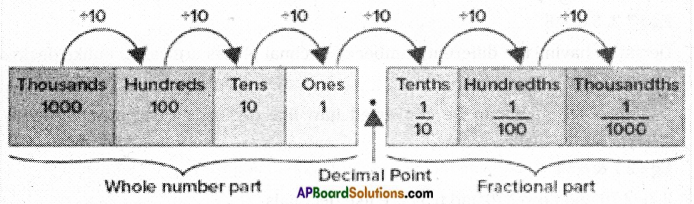
These are also called the place values of the decimal part.
If we divide a whole number into ten equal parts each part of the whole represents tenths part. \(\frac{1}{10}\)
If we divide a whole number into hundred equal parts each part of the whole represents hundredths part. \(\frac{1}{100}\)
If we divide a whole number into thousand equal parts each part of the whole represents thousandths part. \(\frac{1}{1000}\)
![]()
→ Converting fractions into decimals and vice versa:
Fractions with denominators 10, 100, 1000 can be easily converted into decimals by placing decimal point in the numerator accordingly.
- If the denominator is 10, then we place the decimal point in the numerator after one digit from RHS. The number of decimal places is equal to 1.
Eg: \(\frac{256}{10}\) = 25.6 - If the denominator is 100, then we place the decimal point in the numerator after two digits from RHS. The number of decimal places is equal to two.
Eg: \(\frac{256}{100}\) = 2.56 - If the denominator is 1000, then we place the decimal point in the numerator after three digits from RHS, The number of decimal places is equal to three.
Eg: \(\frac{256}{1000}\) = 0.256 and read as zero point two five six.
→ Decimals Can Also be converted into Conversion of simple fractions into decimal fractions:
To convert simple fractions into decimal numbers:
To convert simple fractions into decimal numbers first convert the denominators to 10/100/1000 accordingly and then place the decimal point in the numerator as required.
Eg: \(\frac{23}{2}\) = 23 × \(\frac{5}{10}\) = \(\frac{115}{10}\) = 11.5
\(\frac{7}{4}\) = 7 × \(\frac{25}{100}\) = \(\frac{175}{100}\) = 1.75
\(\frac{3}{5}\) = 3 × \(\frac{2}{10}\) = \(\frac{6}{10}\) = 0.6
Writing zeroes at the end of a decimal number does not change its value.
Eg: 5.2 = 5.20 = 5.200 = 5.2000 and so on
Like and unlike decimal fractions:
Decimals having the same number of decimal places are called like decimals.
Eg: 3.2,5.6,4.8.
Decimals having the different number of decimal places are called unlike decimals. Eg : 5.23, 8.3, 4.214
Unlike decimals can be converted into like decimals by converting them into equivalent decimals.
Eg: 2.7 & 6.54
2.7= 2.70 and now-2.70 and 6.54 are like decimals.
![]()
→ Comparing and ordering of decimals:
To compare the given decimals
a) First convert them to like decimals.
b) Now compare the integer / whole number part. The number with greater whole part is greater than the other.
c) If the whole / integer parts are equal, then compare the tenths digits. The number with greater tenths digit is greater than the other.
d) If the tenths digits are also equal, then compare the hundredths digits. The number with greater hundredths digit is greater than the other.
e) If the hundredths digits are also equal, then compare the thousandths digits. The number with greater thousandths digit is greater than the other.
Eg : 54.235 and 54.238
54.235 < 54.238
→ Addition and subtraction of decimal fractions:
To add or subtract the given decimal fractions first convert them into like decimals. Now add / subtract the digits in the corresponding place values.
→ Uses of decimals: Decimal fractions are used in expressing money, distance, weight and capacity.