AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions Ex 11.1

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions Ex 11.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson Algebraic Expressions Exercise 11.1

Question 1.
Find the product of the following pairs:
(i) 6, 7k
(ii) – 31, – 2m
(iii) -5t² – 3t²
(iv) 6n, 3m
(v) – 5p², – 2p
Solution:
The product of 6, 7k = 6 × 7k = 42k
ii) The product of – 3l, – 2m = (- 3l) × (- 2m) = 6/m
iii) The product of – 5t², – 3t² = (- 5t²) × (- 3t²) = 15t⁴
iv) The product of 6n, 3m = 6n × 3m = 18mn
v) The product of – 5p², – 2p = (- 5p²) × (- 2p) = 10p³

Question 2.
Complete the table of the products.

Solution:

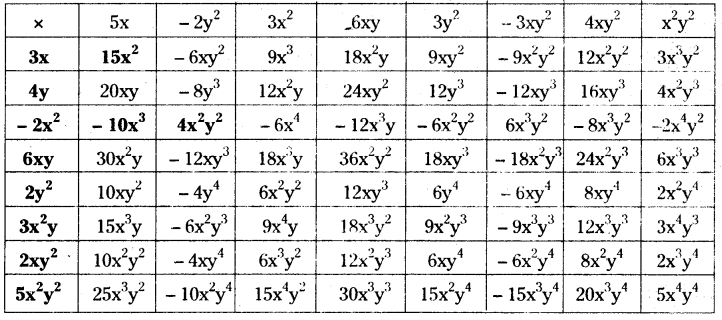
Question 3.
Find the volumes of rectangular boxes with given length, breadth and height in the following table.

Solution:

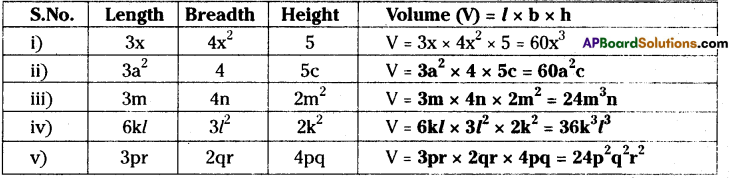
Question 4.
Find the product of the following monomials
(i) xy, x²y , xy, x
(ii) a, b, ab, a³ b, ab³
(iii) kl, lm, km, klm
(iv) pq ,pqr, r
(v) – 3a, 4ab, – 6c, d
Solution:
i) The product of xy, x²y, xy, x = xy × x²y × xy × x
= x⁵ × y³= x⁵y³

ii) The product of a, b, ab, a³b, ab³ = a × b × ab × a³b × ab³
= a⁶ × b⁶ = a⁶ b⁶

iii) The product of kl, lm, km, klm = kl × lm × km × klm
k³ × l³ × m³ =k³l³m³

iv) The product of pq, pqr, r = pq × pqr × r
= p² × q² × r² – p²q²r²

v) The product of – 3a, 4ab, – 6c, d = (- 3a) × 4ab × (- 6c) x d
= + 72a² × b × c × d
= 72a²bcd

Question 5.
If A = xy,B = yz and C = zx, then find ABC=
Solution:
ABC = xy × yz × zx = x²y²z²

Question 6.
If P = 4x², T = 5x and R = 5y, then \(\frac{\mathrm{PTR}}{100}\) =
Solution:
\(\frac{P^{\prime} \Gamma R}{100}=\frac{4 x^{2} \times 5 x \times 5 y}{100}=\frac{100 x^{3} y}{100}\) = x³ y

Question 7.
Write some monomials of your own and find their products.
Solution:
The product of,some monomials is given below :
i) abc × a²bc = a³b²c²
ii) xy × x²z × yz² = x³y²z³
iii) p × q × r = p³q³r³