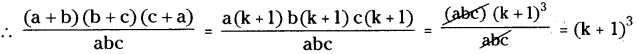AP State Syllabus AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions Ex 11.3 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 11th Lesson Algebraic Expressions Exercise 11.3
![]()
Question 1.
Multiply the binomials:
(i) 2a – 9 and 3a + 4
(ii) x – 2y and 2x – y
(iii) kl + lm and k – l
(iv) m2 – n2 and m + n
Solution:
i) 2a – 9 and 3a + 4
(2a – 9) (3a + 4) = 2a (3a + 4) – 9(3a + 4)
= 6a2 + 8a – 27a – 36
= 6a2 – 19a – 36
ii) x – 2y and 2x – y
(x – 2y) (2x – y) = x(2x – y) – 2y(2x – y)
= 2x2 – xy – 4xy + 2y2
= 2x2 – 5xy + 2y2
iii) kl + lm and k – l
(kl + lm) (k – l) = kl(k – l) + lm(k – l)
= k2l – l2k + klm – l2m
iv) m2 – n2 and m + n
(m2 – n2) (m + n) = m2(m + n) – n2(m + n)
= m3 + m2n – n2m – n3
![]()
Question 2.
Find the product:
(i) (x + y)(2x – 5y + 3xy)
(ii) (mn – kl + km) (kl – lm)
(iii) (a – 2b + 3c)(ab2 – a2b)
(iv) (p3 + q3)(p – 5q+6r)
Solution:
i) (x + y) (2x – 5y + 3xy)
= x(2x – 5y + 3xy) + y(2x – 5y + 3xy)
= 2x2 – 5xy + 3x2y + 2xy – 5y2 + 3xy2
= 2x2 – 5y2 – 3xy + 3x2y + 3xy2
ii) (mn – kl + km) (kl – lm)
= kl(mn – kl + km) – lm(mn – kl + km)
= klmn – k2l2 + k2lm – lm2n + kl2m – klm2
iii) (a – 2b + 3c) (ab2 – a2b) = a(ab2 – a2b) – 2b(ab2 – a2b) + 3c(ab2– a2b)
= a2b2 – a3b – 2ab3 + 2a2b2 + 3ab2c – 3a2bc
= 3a2b2 – a3b – 2ab3 + 3ab2c – 3a2bc
iv) (p3 + q3) (p – 5q + 6r) = p3(p – 5q + 6r) + q3(p – 5q + 6r)
= p4 – 5p3q + 6p3r + pq3 – 5q4 + 6rq3
= p4 – 5q4 – 5p3q + 6p3r + pq3 + 6rq3
![]()
Question 3.
Simplify the following:
(i) (x-2y) (y – 3x) + (x+y) (x-3y) – (y – 3x) (4x – 5y)
(ii) (m + n) (m2 – mn + n2)
(iii) (a – 2b + 5c) (a – b) – (a – b – c) (2a + 3c) + (6a + b) (2c – 3a – 5b)
(iv) (pq-qr-i-pr) (pq-i-qr) – (pr-i-pq) (p-i-q – r)
Solution:
i) (x – 2y) (y – 3x) + (x + y) (x – 3y) – (y – 3x) (4x – 5y)
= (y – 3x) [x – 2y – (4x – 5y)] + (x + y)(x – 3y)
= (y – 3x) [x – 2y – 4x + 5y] + (x + y) (x – 3y)
= (y – 3x) (3y – 3x) + (x + y) (x – 3y)
= y(3y – 3x) – 3x(3y – 3x) + x(x – 3y) + y(x – 3y)
= 3y2 – 3xy – 9xy + 9x2 + x2 – 3xy + xy – 3y2
= 10x2 – 14xy
ii) (m + n) (m2– mn + n2)
= m(m2 – mn + n2) + n(m2 – mn + n2)
= m3 – m2n + n2m + nm2 – mn2 + n3
= m3 + n3
iii) (a – 2b + 5c) (a – b) – (a – b – c) (2a + 3c) + (6a + b) (2c – 3a – 5b)
= a(a – 2b + 5c) – b(a – 2b + 5c) – 2a(a – b – c) – 3c(a – b – c) + 6a(2c – 3a – 5b) + b(2c – 3a – 5b)
= a2 – 2ab + 5ac – ab + 2b2 – 5bc – 2a2 + 2ab + 2ac – 3ac + 3bc + 3c2 + 12ac – 18a2 – 30ab + 2bc – 3ab – 5b2
= – 19a2 – 3b2 – 34ab + 16ac + 3c2
![]()
iv) (pq – qr + pr) (pq + qr) – (pr + pq) (p + q – r)
= pq(pq – qr + pr) + qr(pq – qr + pr) – pr(p + q – r) – pq(p + q – r)
= p2q2 – pq2r + p2qr + pq2r – q2r2 + pqr2 – p2r – pqr + pr2 – p2q – pq2 + pqr
= p2q2 – q2r2 + p2qr + pqr2 – p2r + pr2 – p2q – pq 2
Question 4.
If a, b, care positive real numbers such that \(\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}\) ,find the value of \(\frac{(a+b)(b+c)(c+a)}{a b c}\)
Solution:
\(\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}\) = k then
\(\frac{a+b-c}{c}\) = k ⇒ a + b – c = kc
⇒ a + b = (ck + c) = c(k + 1) …………… (1)
Similarly b + c = a(k + 1) ……………(2)
c + a = b(k + 1) ………………..(3)