AP State Syllabus 8th Class Maths Solutions 14th Lesson Surface Areas and Volume (Cube-Cuboid) InText Questions
AP State Syllabus AP Board 8th Class Maths Solutions Chapter 14 Surface Areas and Volume (Cube-Cuboid) InText Questions and Answers.
8th Class Maths 14th Lesson Surface Areas and Volume (Cube-Cuboid) InText Questions and Answers
Do this
Question 1.
Find the total surface area of the following cuboid. [Page No. 298]
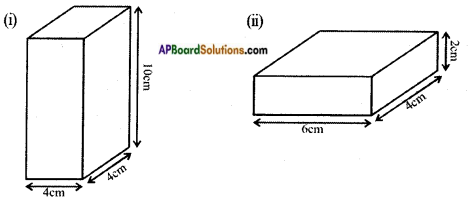
Answer:
i) l = 4 cm, b = 4 cm, h = 10 cm.
The total surface area of a cuboid = 2 (lb + bh + lh)
= 2 (4 × 4 + 4 × 10 + 4 × 10) = 2(16 + 40 + 40)
= 2 × 96
= 192 Sq. cms.
![]()
ii) l = 6 cm, b = 4 cm, h = 2 cm.
The total surface area of a cuboid = 2 (lb + bh + lh)
= 2(6 × 4 + 4 × 2 + 6 × 2)
= 2 (24 + 8 + 12)
= 2 × 44
= 88 sq. cms.
Question 2.
Let us find the volume of a cuboid whose length, breadth and height are 6 cm, 4 cm and 5 cm respectively. [Page No. 287]
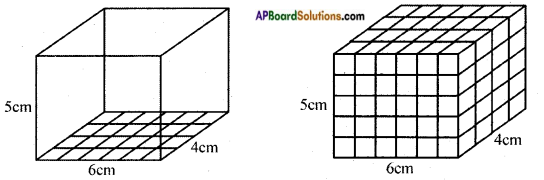
Let place 1 cubic centimeter blocks along the length of the cuboid. How many blocks can we place along the length? 6 blocks, as the length of the cuboid is 6 cm.
How many blocks can we place along its breadth? 4 blocks, as the breadth of the cuboid is 4 cm. So there are 6 × 4 blocks can be placed in a layer.
How many layers of blocks can be placed in the cuboid? 5 layers, as the height of the cuboid is 5 cm. Each layer has 6 × 4 blocks. So, all the 5 layers will have 6 × 4 × 5 blocks i.e. length × breadth × height.
This discussion leads us to the formula for the volume of a cuboid.
Volume of a cuboid = length × breadth × height [Page No. 305]
Answer:
The dimensions of a cuboid are 6 cm, 4 cm, 5 cm respectively.
∴ Volume (V) = lbh
= 6 × 4 × 5.
= 120 cm3
![]()
Question 3.
Arrange 64 unit cubes in as many ways as you can to form a cuboid. Find the surface area of each arrangement. Can solid cuboid of same volume have same surface area? [Page No. 306]
Answer:
No. of cuboids are formed using 64 unit cubes
64 = 1 × 64 ……. (1)
= 2 × 32 …….. (2)
= 4 × 16 …….. (3)
1) l = 64 cm, b = 1 cm, h = 1 cm.
The total surface area of a cuboid, A = 2 (lb + bh + lh)
= 2 (64 × 1 + 1 × 1 + 1 × 64)
= 2 (64 + 1 + 64)
= 2 × 129
= 258 Sq. cm.
2) l = 32 cm, b = 2 cm, h = 1 cm.
A = 2 (lb + bh + lh)
= 2 (32 × 2 + 2 × 1 + 32 × 1)
= 2 (64 + 2 + 32)
= 2 × 98 = 196 Sq. cm.
3) l = 16 cm, b = 4 cm, h = 1 cm.
A = 2 (lb + bh + lh)
= 2 (16 × 4 + 4 × 1 + 16 × 1)
= 2 (64 + 4 + 16)
= 2 × 84 = 168 Sq. cm.
No, the volume of a cuboid is not same as the surface area of a cuboid.
Try These
![]()
Question 1.
Find the surface area of cube ‘A’ and lateral surface area of cube ‘B’. [Page No. 300]
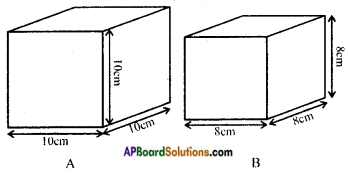
Answer:
a = 10 cm.
The total surface area of a figure ‘A’ = 6a2
= 6 × (10)2
= 6 × 100 = 600 Sq. cm.
Lateral surface area of a figure ‘B’ – 4a2
= 4 × (8)2 [∵ a = 8 cm.]
= 4 × 64 = 256 Sq. cm.
Question 2.
Two cubes each with side ‘b’ are joined to form a cuboid as shown in the given fig. What is the total surface area of this cuboid? [Page No. 300]
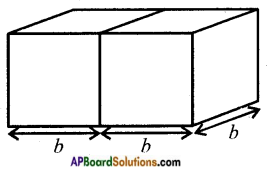
Answer:
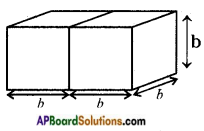
Total surface area of a cuboid = 2 (lb + bh + lh)
= 2 (2b × b + b × b + 2b × b)
= 2 (2b2 + b2 + 2b2)
= 2(5b2) = 10b2 Sq. cm.
![]()
Question 3.
How will you arrange 12 cubes of equal lengths to form a cuboid of smallest surface area? [Page No. 300]

Answer:
We can’t obtain the least total surface area by arranging 12 cubes by side by side.
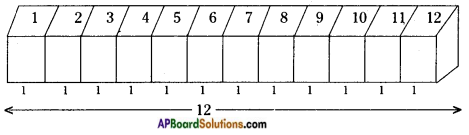
∴ A = 2 (lb + bh + lh)
= 2 (12 × 1 + 1 × 1 + 12 × 1)
= 2 (12 + 1 + 12)
= 2 × 25 = 50 Sq. cm.
We can obtain the least total surface area by arranging 3 cubes by 4 cubes.
∴ A = 2 (lb + bh + lh)
= 2 (3 × 1 + 1 × 4 + 3 × 4) (∵ l = 3; b = 1; h = 4)
= 2 (3 + 4 + 12)
= 2 × 19
= 38 Sq. cm.
Question 4.
The surface area of a cube of 4 × 4 × 4 dimensions is painted. The cube is cut into 64 equal cubes. How many cubes have
(a) 1 face painted? (b) 2 faces painted? (c) 3 faces painted? (d) no face painted? [Page No. 300]
Answer:
If the 4 × 4 × 4 cube is divided into 64 equal cubes then the length of its each side = 1 unit.
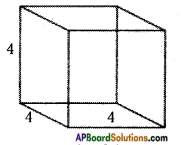
[∵ \(\frac{4 \times 4 \times 4}{64}\) = 1]
a) No.of cubes (a = 4) have painted 1 face = 6(a – 2)2 = 6(4 – 2)2 = 6 × 4 = 24
b) No.of cubes have painted 2 faces = 12(a – 2) = 12(4 – 2) = 24
c) No.of cubes have painted 3 faces = 4 × a = 4 × 2 = 8
d) No.of cubes have painted no faces = (a – 2)3 = (4 – 2)3 = (2)3 = 8
Think, Discuss and Write
![]()
Question 1.
Can we say that the total surface area of cuboid = lateral surface area + 2 × area of base. [Page No. 299]
Answer:
Total surface area of a cuboid = L.S.A + 2 × Area of base
= 2h (l + b) + 2 × lb
= 2lh + 2bh + 2lb
= 2 (lb + bh + lh)
We can conclude that total surface area of a cuboid = L.S.A + 2 × Area of base
Question 2.
If we change the position of cuboid from Fig. (i) to Fig. (ii) do the lateral surface areas become equal? [Page No. 299]
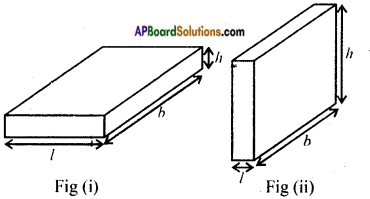
Answer:
There will be no change in the L.S.A of a cuboid if its positions are changed.
![]()
Question 3.
Draw a figure of cuboid whose dimensions are l, b, h are equal. Derive the formula for LSA and TSA. [Page No. 299]
Answer:
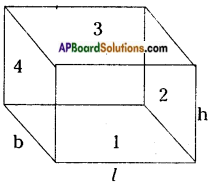
Lateral surface area of a cuboid
= 4 × (areas of 4 faces)
= 2 (l × h) + 2 × (b × h) (1 + 2 + 3 + 4 faces)
= 2h(l + b) sq.units (1 = 3, 4 = 2)
∴ Total surface area of a cuboid
= 4 × (Area of 4 faces) + (Areas of upper & lower faces)
= 2h (l + b) + 2 (lb)
= 2lh + 2bh + 27b
= 2 (lb + bh + lh) sq.units.