AP Inter 1st Year Maths 1A Important Questions Chapter 8 విలోమ త్రికోణమితీయ ప్రమేయాలు

Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 8 విలోమ త్రికోణమితీయ ప్రమేయాలు which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1A Important Questions Chapter 8 విలోమ త్రికోణమితీయ ప్రమేయాలు

సాధించిన సమస్యలు
(Solved Problems)

1. క్రింది వాటి విలువలు కనుక్కోండి.

i) sin^-1 \(\left(-\frac{1}{2}\right)\)
సాధన:
sin^-1\(\left(-\frac{1}{2}\right)\) = –\(\frac{\pi}{6}\)
–\(\frac{\pi}{6}\) ∈ \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)

ii) cos^-1 \(\left(-\frac{\sqrt{3}}{2}\right)\)
సాధన:
cos^-1 \(\left(-\frac{\sqrt{3}}{2}\right)\) = π – cos^-1\(\left(\frac{\sqrt{3}}{2}\right)\)
= π – \(\frac{\pi}{6}\) = \(\frac{5 \pi}{6}\) ∈ [0, π]

iii) tan^-1 \(\left(\frac{1}{\sqrt{3}}\right)\)
సాధన:
tan^-1 \(\left(\frac{1}{\sqrt{3}}\right)\) = \(\frac{\pi}{6}\) ∈ (-\(\frac{\pi}{2}\), \(\frac{\pi}{2}\) )

iv) cot1 (-1)
సాధన:
cot ‘(-1) = π – cot^-1 (1) = π – \(\frac{\pi}{4}\) = \(\frac{3 \pi}{4}\) ∈ (0, π)

v) sec^-1 (-\(\sqrt{2}\))
సాధన:
sec^-1 (-\(\sqrt{2}\)) = π – sec^-1 (\(\sqrt{2}\))
= π – \(\frac{\pi}{4}\) = \(\frac{3 \pi}{4}\) ∈ (\(\frac{\pi}{2}\), π)

vi) cosec^-1 \(\left(\frac{2}{\sqrt{3}}\right)\)
సాధన:
cosec^-1 \(\left(\frac{2}{\sqrt{3}}\right)\) = sin^-1\(\left(\frac{\sqrt{3}}{2}\right)\) = \(\frac{\pi}{3}\) ∈ (0, \(\frac{\pi}{2}\))

ప్రశ్న 2.
క్రింది వాటి విలువలు కనుక్కోండి.

i) sin^-1 (sin \(\frac{4 \pi}{3}\))
సాధన:

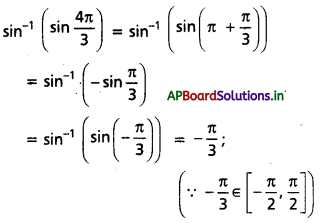
ii) cos^-1 \(\left(\cos \frac{4 \pi}{3}\right)\)
సాధన:

iii) tan^-1 (tan \(\frac{4 \pi}{3}\))
సాధన:

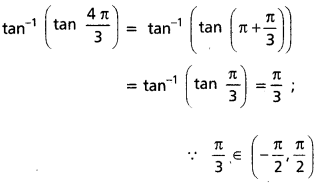
ప్రశ్న 3.
క్రింది వాటి విలువలు కనుక్కోండి.

i) sin (cos^-1 \(\frac{5}{13}\))
సాధన:
sin (cos^-1 \(\frac{5}{13}\)) = sin (sin^-1 \(\frac{12}{13}\)) = \(\frac{12}{13}\)

ii) tan (sec^-1 \(\frac{25}{7}\))
సాధన:
tan(sec^-1\(\frac{25}{7}\)) = tan(tan^-1 \(\frac{24}{7}\)) = \(\frac{24}{7}\)

iii) cos (tan^-1 \(\frac{24}{7}\))
సాధన:
cos (tan^-1 \(\frac{24}{7}\)) = cos (cos^-1 \(\frac{7}{25}\)) = \(\frac{7}{25}\)

ప్రశ్న 4.
క్రింది వాటి విలువలు కనుక్కోండి.

i) sin² (tan^-1 \(\frac{3}{4}\))
సాధన:
sin(tan^-1 \(\frac{3}{4}\)) = sin (sin^-1 \(\frac{3}{5}\)) = \(\frac{3}{5}\)
∴ sin² (tan^-1 \(\frac{3}{4}\)) = (\(\frac{3}{5}\))² = \(\frac{9}{25}\)

ii) sin (\(\frac{\pi}{2}\) – sin^-1 \(\left(-\frac{4}{5}\right)\))
సాధన:

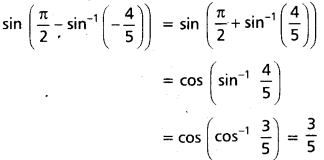
iii) cos (cos^-1\(\left(-\frac{2}{3}\right)\) – sin^-1 \(\left(\frac{2}{3}\right)\))
సాధన:

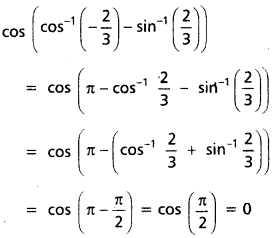
iv) sec² (cot^-1 3) + cosec² (tan^-1 2)
సాధన:
cot^-1 (3) = α, tan^-1(2) = β అనుకుంటే
cot α = 3, tan β = 2
⇒ tan α = \(\frac{1}{3}\), cot β = \(\frac{1}{2}\)
ఇప్పుడు sec²(cot^-1 3) + cosec²(tan^-1 β)
= 1 + \(\left(\frac{1}{3}\right)^2\) + 1 + \(\left(\frac{1}{2}\right)^2\)
= 2 + \(\frac{1}{9}\) + \(\frac{1}{4}\)
= \(\frac{72+4+9}{36}\) = \(\frac{85}{36}\)

iv) sec²(cot^-1 3) + cosec² (tan^-1 2)
సాధన:
cot^-1 (3) = α, tan^-1 (2) = β అనుకుంటే
cot α = 3, tan β = 2
⇒ tan α = \(\frac{1}{3}\), cot β = \(\frac{1}{2}\)

ప్రశ్న 5.
cot^-1 \(\frac{1}{2}\) + cot^-1 \(\frac{1}{3}\) విలువ కనుక్కోండి.
సాధన:
cot^-1 (\(\frac{1}{2}\)) + cot^-1 (\(\frac{1}{3}\))
= tan^-1 (2) + tan^-1 (3)
∵ x = 3, y = 2, xy > 1
= π + tan^-1 \(\left(\frac{2+3 .}{1-(2)(3)}\right)\)
= π + tan^-1 \(\left(\frac{5}{-5}\right)\)
= π + tan^-1 (-1)
= π – \(\frac{\pi}{4}\) = \(\frac{3 \pi}{4}\)

ప్రశ్న 6.
sin^-1 \(\frac{4}{5}\) + sin^-1 \(\frac{7}{25}\) = sin^-1 \(\frac{117}{125}\) అని చూపండి. (Mar. ’13)
సాధన:
మొదటి పద్ధతి :

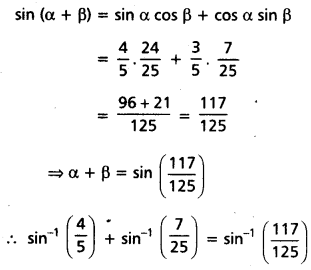
రెండవ పద్ధతి:
x > 0, y > 0, x² + y² < 1 అయితే
sin^-1 x + sin^-1 y = sin (x\(\sqrt{1-y^2}\) + y\(\sqrt{1-x^2}\)), అని మనకు తెలుసు.
∴ sin^-1 \(\frac{4}{5}\) + sin^-1 \(\frac{7}{25}\)

ప్రశ్న 7.
x ∈ (-1, 1) save 2 tan^-1x = tan^-1 \(\left(\frac{2 x}{1-x^2}\right)\) అని రుజువు చేయండి.
సాధన:
∵ x ∈ (-1, 1), tan^-1 x = α అనుకుంటే

ప్రశ్న 8.
sin^-1 \(\frac{4}{5}\) + sin^-1 \(\frac{5}{13}\) + sin^-1 \(\left(\frac{16}{25}\right)\) = \(\frac{\pi}{2}\) అని రుజువు చేయండి.
సాధన:
sin^-1 \(\frac{4}{5}\) = α, sin^-1 \(\frac{5}{13}\) = β అనుకుంటే
α, β లు అల్పకోణాలు.
sin α = \(\frac{4}{5}\), sin β = \(\frac{5}{13}\)
కనుక cos α = \(\frac{3}{5}\), cos β = \(\frac{12}{13}\)
ఇప్పుడు
cos (α + β) = cos α cos β – sin α sin β
= \(\frac{3}{5}\). \(\frac{12}{13}\) – \(\frac{4}{5}\) . \(\frac{5}{13}\)
= \(\frac{16}{65}\)
∴ α + β = cos^-1 \(\left(\frac{16}{65}\right)\)

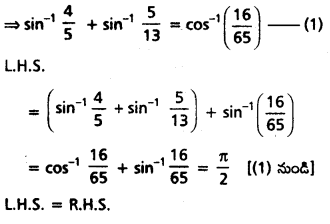
ప్రశ్న 9.
cot^-1 9 + cosec^-1 \(\frac{\sqrt{41}}{4}\) = \(\frac{\pi}{4}\) అని రుజువు చేయండి.
సాధన:
cot^-1 (9) = α, cosec^-1\(\frac{\sqrt{41}}{4}\) = β అనుకుంటే
cot α = 9, cosec β = \(\frac{\sqrt{41}}{4}\) అవుతాయి.

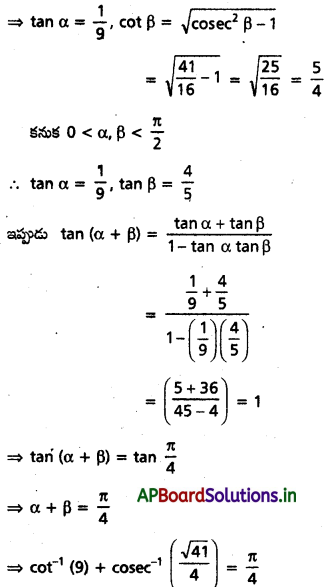
ప్రశ్న 10.
cot (sin^-1 \(\sqrt{\frac{13}{17}}\)) = sin (tan^-1 \(\frac{2}{3}\)) అని చూపండి.
సాధన:

ప్రశ్న 11.
tan ((2 tan^-1 \(\frac{1}{5}\)) – \(\frac{\pi}{4}\) విలువను కనుక్కోండి.
సాధన:

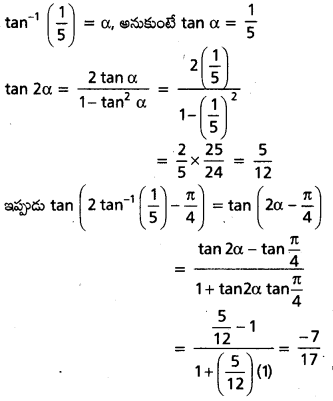
ప్రశ్న 12.
sin^-1 \(\frac{4}{5}\) + 2 tan^-1 \(\frac{1}{3}\) = \(\frac{\pi}{2}\) అని రుజువు చేయండి.
సాధన:

ప్రశ్న 13.
cos (2 tan^-1 \(\frac{1}{7}\)) = sin (4 tan^-1 \(\frac{1}{3}\)) అని రుజువు చేయండి.
సాధన:

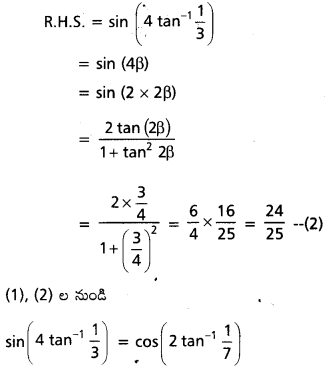
ప్రశ్న 14.
sin^-1 x + sin^-1y + sin^-1 z = π, అయితే x⁴ + y⁴ + z⁴ + 4x²y²z² = 2(x²y² + y²z² + z²x²) అని చూపండి.
సాధన:
sin^-1x = A, sin^-1 y = B, sin^-1 (z) = C అనుకుందాం
sin A = x, sin B = y, sin C = z
A + B = π – C
⇒ cos (A + B) = cos(π – C)
⇒ cos A cos B – sin A sin B = -cos C

ప్రశ్న 15.
cos^-1\(\frac{\mathbf{p}}{\mathbf{a}}\) + cos^-1\(\frac{\mathbf{q}}{\mathbf{b}}\) = α, అయితే \(\frac{p^2}{a^2}\) – 2\(\frac{p q}{a b}\) cos α + \(\frac{q^2}{b^2}\) = sin² α అని రుజువు చేయండి.
సాధన:

ప్రశ్న 16.
x > 0 కు arc sin\(\left(\frac{5}{x}\right)\) + arc sin \(\frac{12}{x}\) = \(\frac{\pi}{2}\)
ను సాధించండి.
సాధన:

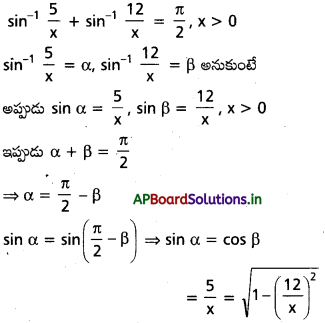
⇒ \(\frac{25}{x^2}\) = 1 – \(\frac{144}{x^2}\)
⇒ \(\frac{169}{x^2}\) = 1 ⇒ x² = 169 ⇒ x = ± 13
⇒ x = 13 (∵ x > 0)

ప్రశ్న 17.
sin^-1 \(\left(\frac{3 x}{5}\right)\) + sin^-1 \(\left(\frac{4 x}{5}\right)\) = sin^-1(x) ను సాధించండి.
సాధన:
sin^-1 \(\left(\frac{3 x}{5}\right)\) = α, sin^-1 \(\left(\frac{4 x}{5}\right)\) = β, sin^-1 (x) = γ అనుకుంటే
అప్పుడు sin α = \(\frac{3 x}{5}\), sin β = \(\frac{4 x}{5}\), sin γ = x అవుతాయి

⇒ 25 – 16x² = 9
⇒ 16x² = 16 ⇒ x = ±1
∴ x = 0, +1, -1
x యొక్క ఈ విలువలు దత్త సమీకరణాన్ని సంతృప్తిపరుస్తాయి.

ప్రశ్న 18.
sin^-1x + sin^-1 2x = \(\frac{\pi}{3}\) ను సాధించండి.
సాధన:

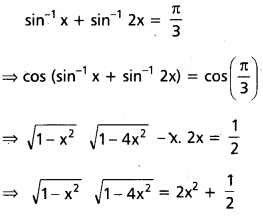
ఇరువైపులా వర్గం చేస్తే

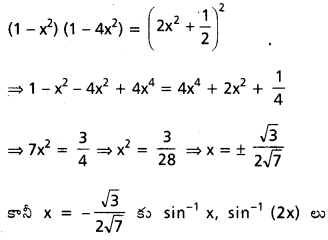
ఋణాత్మకాలు. కనుక ఈ విలువ దత్త సమీకరణాన్ని సంతృప్తిపరచదు.
x = \(\frac{\sqrt{3}}{2 \sqrt{7}}\) మాత్రమే సాధన.

ప్రశ్న 19.
sin [2 cos^-1 {cot (2 tan^-1 x)}] = 0, అయితే x ను కనుక్కోండి.
సాధన:
sin [2cos^-1 {cot (2 tan^-1 x)}] = 0
⇔ 2 cos^-1 [cot (2tan‍^-1 x)] = 0 లేదా π లేదా 2π
(cos^-1 x యొక్క వ్యాప్తి [0, π] కనుక)
⇔ cos^-1 [cot (2 tan^-1 x)] = 0 లేదా \(\frac{\pi}{2}\) లేదా π
⇔ cot (2 tan^-1 x) = 1 లేదా 0 లేదా −1

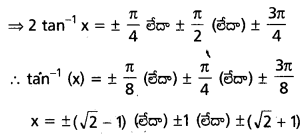
ప్రశ్న 20.
cos [tan^-1 {sin (cot ^-1x)}] = \(\sqrt{\frac{x^2+1}{x^2+2}}\) అని నిరూపించండి.
సాధన:
cot^-1 (x) = θ అనుకుందాం.
అప్పుడు cot θ = x, 0 < x < π