AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Ex 3(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 3 మాత్రికలు Exercise 3(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Exercise 3(a)

I.

Question 1.
ఈ క్రిందివాటిని ఒకే మాత్రికగా వ్రాయండి.
(i) [2 1 3] + [0 0 0]
(ii) \(\left[\begin{array}{c}
0 \\
1 \\
-1
\end{array}\right]+\left[\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right]\)
(iii) \(\left[\begin{array}{ccc}
3 & 9 & 0 \\
1 & 8 & -2
\end{array}\right]+\left[\begin{array}{ccc}
4 & 0 & 2 \\
7 & 1 & 4
\end{array}\right]\)
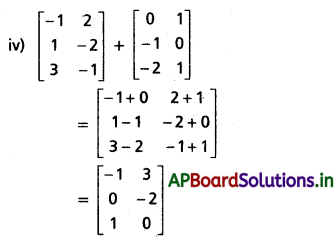
(iv) \(\left[\begin{array}{cc}
-1 & 2 \\
1 & -2 \\
3 & -1
\end{array}\right]+\left[\begin{array}{cc}
0 & 1 \\
-1 & 0 \\
-2 & 1
\end{array}\right]\)
Solution:

Question 2.
A = \(\left[\begin{array}{cc}
-1 & 3 \\
4 & 2
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 1 \\
3 & -5
\end{array}\right]\), X = \(\left[\begin{array}{ll}
x_1 & x_2 \\
x_3 & x_4
\end{array}\right]\), A + B = X అయితే x₁, x₂, x₃, x₄ ల విలువలు కనుక్కోండి.
Solution:
A + B = X కనుక

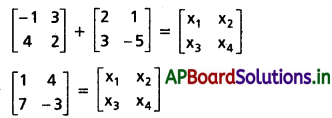
∴ x₁ = 1, x₂ = 4, x₃ = 7, x₄ = -3

Question 3.
A = \(\left[\begin{array}{ccc}
-1 & -2 & 3 \\
1 & 2 & 4 \\
2 & -1 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -2 & 5 \\
0 & -2 & 2 \\
1 & 2 & -3
\end{array}\right]\), C = \(\left[\begin{array}{ccc}
-2 & 1 & 2 \\
1 & 1 & 2 \\
2 & 0 & 1
\end{array}\right]\) అయితే A + B + C ని కనుక్కోండి.
Solution:

Question 4.
A = \(\left[\begin{array}{ccc}
3 & 2 & -1 \\
2 & -2 & 0 \\
1 & 3 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
3 & 2 & -1 \\
2 & -2 & 0 \\
1 & 3 & 1
\end{array}\right]\), X = A + B అయితే, మాత్రిక X ను కనుక్కోండి.
Solution:

Question 5.
\(\left[\begin{array}{cc}
x-3 & 2 y-8 \\
z+2 & 6
\end{array}\right]=\left[\begin{array}{cc}
5 & 2 \\
-2 & a-4
\end{array}\right]\) అయితే x, y, z, a విలువలను కనుక్కోండి. [May ’06]
Solution:
\(\left[\begin{array}{cc}
x-3 & 2 y-8 \\
z+2 & 6
\end{array}\right]=\left[\begin{array}{cc}
5 & 2 \\
-2 & a-4
\end{array}\right]\)
∴ x – 3 = 5
⇒ x = 3 + 5 = 8
2y – 8 = 2
⇒ 2y = 8 + 2 = 10
⇒ y = 5
z + 2 = -2
⇒ z = -2 – 2 = -4
a – 4 = 6
⇒ a = 4 + 6 = 10

II.

Question 1.
\(\left[\begin{array}{ccc}
x-1 & 2 & 5-y \\
0 & z-1 & 7 \\
1 & 0 & a-5
\end{array}\right]=\left[\begin{array}{ccc}
1 & 2 & 3 \\
0 & 4 & 7 \\
1 & 0 & 0
\end{array}\right]\) అయితే x, y, z, a ల విలువలు కనుక్కోండి.
Solution:
\(\left[\begin{array}{ccc}
x-1 & 2 & 5-y \\
0 & z-1 & 7 \\
1 & 0 & a-5
\end{array}\right]=\left[\begin{array}{ccc}
1 & 2 & 3 \\
0 & 4 & 7 \\
1 & 0 & 0
\end{array}\right]\)
∴ x – 1 = 1
⇒ x = 1 + 1 = 2
5 – y = 3
⇒ y = 5 – 3 = 2
z – 1 = 4
⇒ z = 4 + 1 = 5
a – 5 = 0
⇒ a = 5

Question 2.
A = \(\left[\begin{array}{ccc}
1 & 3 & -5 \\
2 & -1 & 5 \\
2 & 0 & 1
\end{array}\right]\) అయితే జాడ A కనుక్కోండి. [May ’13]
Solution:
జాడ A = ప్రధాన వికర్ణ మూలకాల మొత్తం
= 1 – 1 + 1
= 1

Question 3.
A = \(\left[\begin{array}{ccc}
0 & 1 & 2 \\
2 & 3 & 4 \\
4 & 5 & -6
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) అయితే B – A, 4A – 5B లను కనుక్కోండి.
Solution:

Question 4.
A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 2 & 1
\end{array}\right]\), B = \(\left[\begin{array}{lll}
3 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]\) అయితే 3B – 2A ను కనుక్కోండి.
Solution:
A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 2 & 1
\end{array}\right]\), B = \(\left[\begin{array}{lll}
3 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]\)