AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Ex 3(h)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 3 మాత్రికలు Exercise 3(h) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Exercise 3(h)

I. కింది సమీకరణ వ్యవస్థలను
(i) గుణక మాత్రిక సాధారణమైనపుడు క్రేమర్ నియమంతోనూ, మాత్రికా విలోమ పద్ధతిలోనూ సాధించండి.
(ii) గౌన్ – జోర్డాన్ పద్ధతిని ఉపయోగించి సాధించండి. ఇంకా వ్యవస్థకు ఏకైక సాధన ఉందా, అనంత సాధనలు ఉన్నాయా, సాధన లేదా అనేది తెలపండి. సాధన ఉంటే సాధించండి.

Question 1.
5x – 6y + 4z = 15
7x + 4y – 3z = 19
2x + y + 6z = 46
సూచన : x = \(\frac{\Delta_1}{\Delta}\), y = \(\frac{\Delta_2}{\Delta}\), z = \(\frac{\Delta_3}{\Delta}\)
Solution:

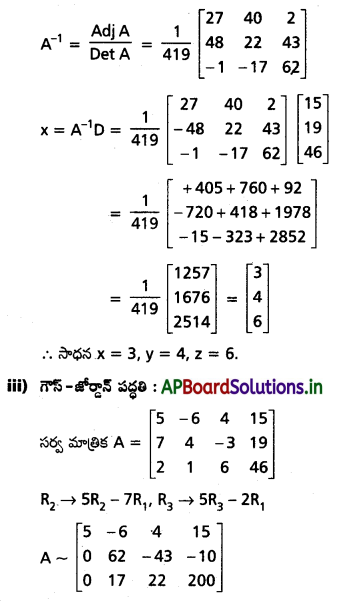
Question 2.
x + y + z = 1
2x + 2y + 3z = 6
x + 4y + 9z = 3
Solution:

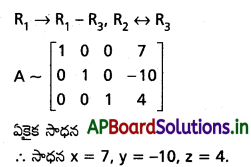
Question 3.
x – y + 3z = 5
4x + 2y – z = 0
-x + 3y + z = 5 [(T.S) Mar. ’15]
Solution:

Question 4.
2x + 6y + 11 = 0
6x + 20y – 6z + 3 = 0
6y – 18z + 1 = 0
Solution:
∆ = \(\left|\begin{array}{ccc}
2 & 6 & 0 \\
6 & 20 & -6 \\
0 & 6 & -18
\end{array}\right|\)
= 2(-360 + 36) – 6(-108 – 0)
= -648 + 648
= 0
∵ ∆ = 0 కనుక.
క్రేమర్ నియమంతోను, మాత్రిక విలోమ పద్ధతిని సాధించలేము.
(ii) గౌస్ – జోర్డాన్ పద్ధతి :

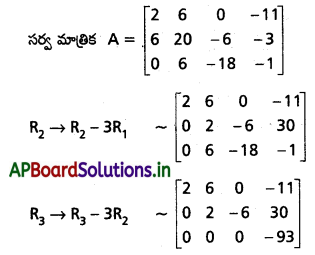
ρ(A) = 2, ρ(AB) = 3
ρ(A) ≠ ρ(AB)
∴ దత్త వ్యవస్థ అసంగతం. సాధన లేదు.

Question 5.
2x – y + 3z = 9
x + y + z = 6
x – y + z = 2 [Mar. ’14, ’05, ’02; May ’13]
Solution:

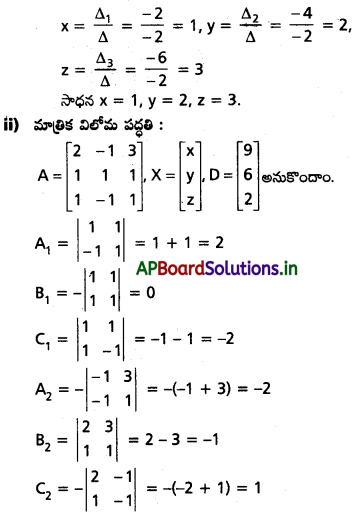
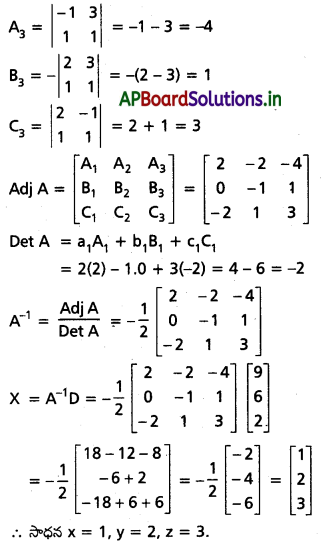
Question 6.
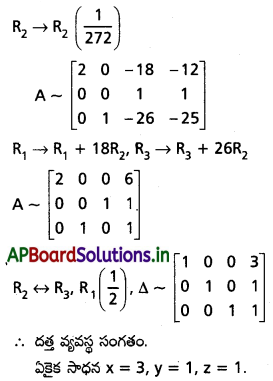
2x – y + 8z = 13
3x + 4y + 5z = 18
5x – 2y + 7z = 20 [Mar. ’04, ’03, ’01]
Solution:

Question 7.
2x – y + 3z = 8
-x + 2y + z = 4
3x + y – 4z = 0
Solution:

Question 8.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Solution: