Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 5 త్రిపరిమాణ నిరూపకాలు Exercise 5(a) will help students to clear their doubts quickly.
AP Inter 1st Year Maths 1B Solutions Chapter 5 త్రిపరిమాణ నిరూపకాలు Exercise 5(a)
అభ్యాసం – 5 (ఎ)
I.
ప్రశ్న 1.
P (3, −2, 4) బిందువుకు మూలబిందువు నుంచి దూరాన్ని కనుక్కోండి.
సాధన:
OP = \(\sqrt{x^2+y^2+z^2}\)
= \(\sqrt{9+4+16}\)
= \(\sqrt{29}\) యూనిట్లు
ప్రశ్న 2.
(3, 4, -2), (1,0,7) బిందువుల మధ్యదూరం కనుక్కోండి.
సాధన:
PQ = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2+\left(z_1-z_2\right)^2}\)
= \(\sqrt{(3-1)^2+(4-0)^2+(-2-7)^2}\)
= \(\sqrt{4+16+81}\)
= \(\sqrt{101}\) యూనిట్లు
![]()
II.
ప్రశ్న 1.
(5, -1, 7), (x, 5,1)ల మధ్యదూరం 9 యూనిట్లు అయితే X ను కనుక్కోండి.
సాధన:
P(5, -1, 7), Q(x, 5, 1) లు దత్త బిందువులు
PQ = 9
PQ = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2+\left(z_1-z_2\right)^2}\) = 9
\(\sqrt{(5-x)^2+(-1-5)^2+(7-1)^2}\) = 9
(5 – x)2 + 36 + 36 = 81
(5 – x)2 = 81 – 72 = 9
5 – x = ±3
5 – x = 3 లేదా 5 – x = -3
x = 5 – 3 లేదా x = 5 + 3
= 2 లేదా 8
![]()
ప్రశ్న 2.
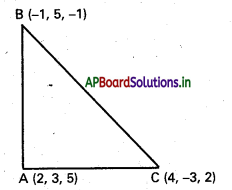
(2, 3, 5), (−1, 5, -1), (4, -3, 2) బిందువులు సమద్విబాహు లంబకోణ త్రిభుజాన్ని ఏర్పరుస్తాయని చూపండి.
సాధన:
A (2, 3, 5), B (-1, 5, -1), C (4, -3, 2) లు దత్త
బిందువుల
AB2 = (2 + 1)2 + (3 – 5)2 + (5 + 1)2
= 9 + 4 + 36
= 49
BC2 = (-1 – 42 + (5 + 3)2 + (-1 – 2)2
= 25 + 64 + 9
= 98
CA2 = (4 – 2)2 + (-3 – 3)2 + (2 – 5)2
= 4 + 36 + 9
= 49
AB2 = CA2
⇒ AB2 + CA2 = 49 + 49 = 98 = BC2
ABC లంబకోణ సమద్విబాహు త్రిభుజం
ప్రశ్న 3.
(1, 2 ,3), (2, 3, 1), (3, 1, 2) బిందువులు ఒక సమబాహు త్రిభుజాన్ని ఏర్పరుస్తాయని చూపండి.
సాధన:
A(1, 2, 3), B(2, 3, 1) మరియు C (3, 1, 2) లు దత్త బిందువులు
AB2 = (1 – 2)2 + (2 – 3)2 + (3 – 1)2
= 1 + 1 +4
= 6
BC2 = (2 – 3)2 + (3 – 1)2 + (1 – 2)2
= 1 + 4 + 1
= 6
CA2 = (3 – 1)2 + (1 – 2)2 + (2 – 3)2
= 4 + 1 + 1
= 6
AB2 = BC2 = CA2
⇒ AB = BC = CA
ABC సమబాహు త్రిభుజము.
![]()
ప్రశ్న 4.
A = (-2, 2, 3), B = (13, -3, 13)∞r Bow Dowser. 3PA = 2PB అయ్యేటట్లు చలించే బిందువు P యొక్క నిరూపకాలు
x2 + y2 + z2 + 28x – 12y + 10z – 247 = 0 సమీకరణాన్ని తృప్తిపరుస్తాయని చూపండి.
సాధన:
A(-2, 2, 3) మరియు B(13, -3, 13) లు దత్త బిందువులు P(x,y,z) బిందువు బిందుపథం మీది దత్త నియమము
3PA = 2PB ⇒ 9 PA2 4PB2
9[(x + 2)2 + (y – 2)2 + (z – 3)2]
= 4 [(x – 13)2 + (y + 3)2 + (z – 13)2]
⇒ 9(x2 + 4x +4 + y2 – 4y + 4 + z2 – 6z + 9)
= 4(x2 – 26x + 169 + y2 + 6y + 9 + z2 – 26z + 169)
= 9x2 + 9y2 + 9z2 + 36x – 36y – 54z + 153
= 4x2 + 4y2 + 4z2 – 104x + 24y – 104z + 1388
5x2 + 5y2 +5z2 + 140x – 60y + 50z – 1235 = 0
5 తో భాగించగా P బిందు పధము x2 + y2 + z2 + 28x – 12y + 10z – 247 = 0
ప్రశ్న 5.
(1, 2, 3) (7, 0, 1), (-2, 3, 4) లు సరేఖీయాలు అని చూపండి. [Mar. ’13]
సాధన:
A (1, 2, 3), B(7, 0, 1) C(-2, 3, 4) లు దత్త బిందువులు
AB = \(\sqrt{(1-7)^2+(2-0)^2+(3-1)^2}\)
= \(\sqrt{36+4+4}=\sqrt{44}\)
= \(2 \sqrt{11}\)
BC = \(\sqrt{(7+2)^2+(0-3)^2+(1-4)^2}\)
= \(\sqrt{81+9+9}=\sqrt{99}\)
= \(3 \sqrt{11}\)
CA = \(\sqrt{(-2-1)^2+(3-2)^2+(4-3)^2}\)
= \(\sqrt{9+1+1}=\sqrt{11}\)
AB + AC = \(2 \sqrt{11}\) + \(\sqrt{11}\) = \(2 \sqrt{11}\) = BC
A, B, C లు సరేఖీయాలు
![]()
ప్రశ్న 6.
(0, 4, 1), (2, 3, 1), (4, 5, 0), (2, 6, 2) లు వరసగా A, B, C, D బిందువులని సూచిస్తే ABCD ఒక చతురస్రం అని చూపండి.
సాధన:
A(0, 4, 1), B(2, 3, -1) C(4, 5, 0), D(2, 6, 2) లు దత్త బిందువులు
AB2 = (0 − 2)2 + (4 – 3)2 + (1 + 1)2
= 4 + 1 + 4
= 9
BC2 = (2 – 4)2 + (3 – 5)2 + (-1 + 0)2
= 4 + 4 + 1
= 9
CD2 = (4 – 2)2 + (5 – 6)2 + (0 − 2)2
= 4 + 1 + 4
= 9
DA2 = (2 – 0)2 + (6 – 4)2 + (2 – 1)2
= 4 + 4 + 1
= 9
AB2 = BC2 = CD2 = DA2
⇒ AB = BC = CD = DA
AC2 = (0 – 4)2 + (4 – 5)2 + (1 – 0)2
= 16 + 1 + 1
= 18
BD2 = (2 – 2)2 + (3 – 6)2 + (-1 – 2)2
= 9 + 9
= 18
AC2 = BD2 → AC = BD
AB2 + BC2 = 9 + 9 = 18 = AC2
⇒ ∠ABC 90°
A, B, C, D లు చతురస్ర శీర్షాలు