AP Inter 1st Year Maths 1A Solutions Chapter 4 సదిశల సంకలనం Ex 4(b)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 4 సదిశల సంకలనం Exercise 4(b) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 4 సదిశల సంకలనం Exercise 4(b)

I.

Question 1.
\(2 \bar{i}+3 \bar{j}+\bar{k}\) బిందువు గుండా పోతూ, \(4 \bar{i}-2 \bar{j}+3 \bar{k}\) సదిశకు సమాంతరంగా ఉండే రేఖ సదిశా సమీకరణం కనుక్కోండి. [(A.P) Mar. ’15, ’07; May ’07]
Solution:

Question 2.
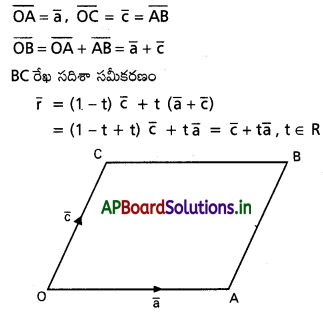
OABC సమాంతర చతుర్భుజంలో, \(\overline{\mathbf{O A}}=\overline{\mathbf{a}}, \overline{\mathbf{O C}}=\overline{\mathbf{C}}\) అయితే, BC రేఖ సదిశా సమీకరణాన్ని కనుక్కోండి. [(T.S) Mar ’15]
Solution:
OABC సమాంతర చతుర్భుజం

Question 3.
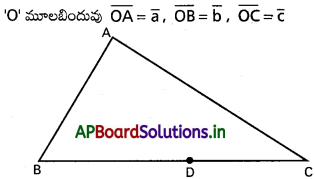
A, B, C బిందువులు ఒక త్రిభుజ శీర్షాలు. వాటి స్థాన సదిశలు క్రమంగా \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) అయితే, A గుండా పోయే మధ్యగత రేఖ సదిశా సమీకరణాన్ని కనుక్కోండి. [Mar. ’13]
Solution:

Question 4.
\(2 \overline{\mathbf{i}}+\overline{\mathbf{j}}+3 \overline{\mathbf{k}},-4 \overline{\mathbf{i}}+\mathbf{3} \overline{\mathbf{j}}-\overline{\mathbf{k}}\) బిందువులను కలిపే రేఖ సదిశా సమీకరణాన్ని కనుక్కోండి. [Mar. ’11; May ’08]
Solution:

Question 5.
\(\overline{\mathbf{i}}-2 \overline{\mathbf{j}}+5 \overline{\mathbf{k}},-5 \overline{\mathbf{j}}-\overline{\mathbf{k}},-3 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}\) బిందువుల గుండా పోయే తలం సదిశా సమీకరణాన్ని కనుక్కోండి. [May ’13]
Solution:

Question 6.
(0, 0, 0), (0, 5, 0), (2, 0, 1) బిందువుల గుండా పోయే తలం సదిశా సమీకరణాన్ని కనుక్కోండి.
Solution:

II.

Question 1.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతలీయ సదిశలు అయితే, \(2 \overline{\mathbf{a}}+3 \overline{\mathbf{b}}-\overline{\mathbf{c}}\), \(3 \bar{a}+4 \bar{b}-2 \bar{c}\) బిందువులను కలిపే రేఖ, \(\overline{\mathbf{a}}-2 \overline{\mathbf{b}}+3 \overline{\mathbf{c}}\), \(\bar{a}-6 \bar{b}+6 \bar{c}\) బిందువులను కలిపే రేఖల ఖండన బిందువును కనుక్కోండి.
Solution:

Question 2.
ABCD సమలంబ చతుర్భుజం (trapezium) లో AB, CD లు సమాంతర భుజాలు. AB, CD ల మధ్య బిందువులు, కర్ణాల ఖండన బిందువు సరేఖీయాలని సదిశా పద్ధతిని వాడి నిరూపించండి.
Solution:
ABCD సమలంబ చతుర్భుజం.
AB, CD లు సమాంతరములు.




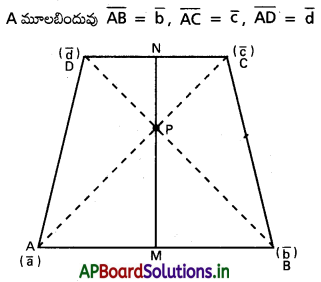
(4), (5) ల నుండి,
\(\overline{\mathrm{PM}}=\lambda(\overline{\mathrm{NP}})\)
M, P, N లు సరేఖీయాలు.
కనుక సమాంతర భుజాల మధ్యబిందువులు, కర్ణాల ఖండన బిందువు సరేఖీయాలు.

Question 3.
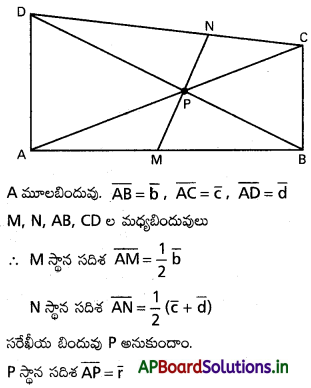
ABCD చతుర్భుజంలో, ఒక జత ఎదుటి భుజాల మధ్య బిందువులూ, దాని కర్ణాల ఖండన బిందువు సరేఖీయాలైతే, ఆ చతుర్భుజం సమలంబ చతుర్భుజం అవుతుందని సదిశా పద్ధతుల ద్వారా నిరూపించండి.
Solution:

III.

Question 1.
\(2 \bar{i}+4 \bar{j}+2 \bar{k}, 2 \bar{i}+3 \bar{j}+5 \bar{k}\) బిందువుల గుండా పోతూ, సదిశ \(3 \overline{\mathbf{i}}-2 \overline{\mathbf{j}}+\overline{\mathbf{k}}\) కు సమాంతరంగా ఉండే తలం సదిశా సమీకరణం కనుక్కుని, \(\mathbf{2} \overline{\mathbf{i}}+\overline{\mathbf{j}}+\mathbf{3} \overline{\mathbf{k}}\), \(4 \overline{\mathbf{i}}-2 \overline{\mathbf{j}}+3 \overline{\mathbf{k}}\) బిందువులను కలిపే రేఖను ఈ తలం ఖండించే బిందువును కూడ కనుక్కోండి. [Mar. ’12]
Solution:

Question 2.
\(4 \overline{\mathbf{i}}-3 \overline{\mathbf{j}}-\overline{\mathbf{k}}, 3 \overline{\mathbf{i}}+7 \overline{\mathbf{j}}-10 \bar{k}, 2 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}-7 \overline{\mathbf{k}}\), బిందువుల ద్వారా పోయే తలం సదిశాసమీకరణం కనుక్కొని, \(\overline{\mathbf{i}}+2 \overline{\mathbf{j}}-3 \overline{\mathbf{k}}\) బిందువు, ఈ తలంలో ఉంటుందని చూపండి. [Mar. ’13]
Solution:


(1), (2), (3) ను ధృవీకరిస్తున్నాయి.
D బిందువు, A, B, C తలంలో ఉంటుంది.