AP Inter 1st Year Maths 1A Solutions Chapter 5 సదిశల గుణనం Ex 5(c)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 5 సదిశల గుణనం Exercise 5(c) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 5 సదిశల గుణనం Exercise 5(c)

I.

Question 1.
\([\bar{i}-\bar{j} \bar{j}-\bar{k} \bar{k}-\bar{i}]\) ను గణన చేయండి.
Solution:
\([\bar{i}-\bar{j} \bar{j}-\bar{k} \bar{k}-\bar{i}]\) = \(\left|\begin{array}{ccc}
1 & -1 & 0 \\
0 & 1 & -1 \\
-1 & 0 & 1
\end{array}\right|\)
= 1(1 – 0) + 1(-1)
= 1 – 1
= 0

Question 2.
\(\overline{\mathbf{a}}=\overline{\mathbf{i}}-2 \overline{\mathbf{j}}-3 \overline{\mathbf{k}}, \overline{\mathbf{b}}=\mathbf{2} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}\), \(\bar{c}=\mathbf{i}+3 \overline{\mathbf{j}}-2 \overline{\mathbf{k}}\) అయితే \(\overline{\mathbf{a}} \cdot(\overline{\mathbf{b}} \times \overline{\mathbf{c}})\) ను గణన చేయండి.
Solution:

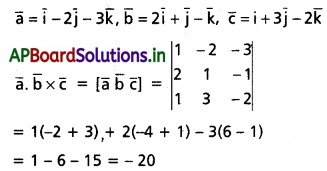
Question 3.
\(\overline{\mathbf{a}}\) = (1, -1, -6), \(\overline{\mathbf{b}}\) = (1, -3, 4), \(\overline{\mathbf{c}}\) = (2, -5, 3), అయితే ఈ కింద వాటిని గణన చేయండి.
(i) \(\overline{\mathbf{a}} \cdot(\overline{\mathbf{b}} \times \overline{\mathbf{c}})\)
(ii) \(\overline{\mathbf{a}} \times(\overline{\mathbf{b}} \times \overline{\mathbf{c}})\)
(iii) \((\overline{\mathbf{a}} \times \overline{\mathbf{b}}) \times \overline{\mathbf{c}}\)
Solution:

Question 4.
ఈ కిందివాటిని సూక్ష్మీకరించండి.
(i) \((\overline{\mathbf{i}}-2 \overline{\mathbf{j}}+3 \overline{\mathbf{k}}) \times(2 \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}) \cdot(\overline{\mathbf{j}}+\overline{\mathbf{k}})\)
(ii) \((2 \bar{i}-3 \bar{j}+\bar{k}) \cdot(\bar{i}-\bar{j}+2 \bar{k}) \times(2 \bar{i}+\bar{j}+\bar{k})\)
Solution:
(i) \((\overline{\mathbf{i}}-2 \overline{\mathbf{j}}+3 \overline{\mathbf{k}}) \times(2 \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}) \cdot(\overline{\mathbf{j}}+\overline{\mathbf{k}})\)
= \(\left|\begin{array}{ccc}
1 & -2 & 3 \\
2 & 1 & -1 \\
0 & 1 & 1
\end{array}\right|\)
= 1(1 + 1) + 2(2 – 0) + 3(2 – 0)
= 2 + 4 + 6
= 12

(ii) \((2 \bar{i}-3 \bar{j}+\bar{k}) \cdot(\bar{i}-\bar{j}+2 \bar{k}) \times(2 \bar{i}+\bar{j}+\bar{k})\)
= \(\left|\begin{array}{ccc}
2 & -3 & 1 \\
1 & -1 & 2 \\
2 & 1 & 1
\end{array}\right|\)
= 2 (-1 – 2) + 3(1 – 4) + 1(1 + 2)
= -6 – 9 + 3
= -12

Question 5.
\(\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{i}}-\overline{\mathbf{j}}, \overline{\mathbf{i}}+\mathbf{2 j}-\overline{\mathbf{k}}\) సదిశలను సహవసానిక భుజాలుగా (Coterminus edges) గా గల సమాంతర ఫలకం ఘనపరిమాణాన్ని కనుక్కోండి.
Solution:

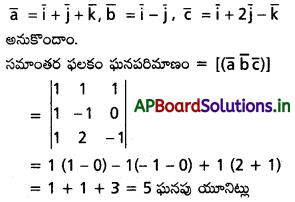
Question 6.
\(\mathbf{2 i}-\mathbf{3} \overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{i}}+\mathbf{2 \mathbf { j }}-\mathbf{3} \overline{\mathbf{k}}, \overline{\mathbf{j}}-\mathbf{t \mathbf { k }}\) సతలీయాలైతే, t ని కనుక్కోండి.
Solution:

Question 7.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతళీయ సదిశలై \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}\), \(\overline{\mathbf{a}}+\mathbf{p} \overline{\mathbf{b}}+\mathbf{2} \overline{\mathbf{c}},-\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}\) సదిశలు సతలీయాలైతే p ని కనుక్కోండి.
Solution:

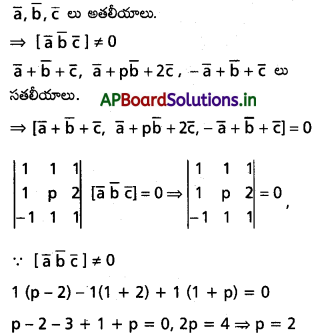
Question 8.
\(\mathbf{i}+\mathbf{j}, 3 \overline{\mathbf{i}}-\overline{\mathbf{j}}, \mathbf{3} \overline{\mathbf{j}}+\lambda \overline{\mathbf{k}}\) సదిశలను సహావసానిక భుజాలు గల సమాంతర ఫలకం ఘనపరిమాణం 16 ఘన యూనిట్లు అయితే λ కనుక్కోండి.
Solution:

Question 9.
\(\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{i}}-\overline{\mathbf{j}}\) మరియు \(\overline{\mathbf{i}}+\mathbf{2} \overline{\mathbf{j}}+\overline{\mathbf{k}}\) సదిశలను అంచులుగా గల చతుర్ముఖి ఘనపరిమాణాన్ని కనుక్కోండి.
Solution:

Question 10.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతలీయ సదిశలు \(\bar{\alpha}=\overline{\mathbf{a}}+2 \bar{b}+3 \bar{c}\), \(\bar{\beta}=\mathbf{2} \overline{\mathbf{a}}+\overline{\mathbf{b}}-\mathbf{2} \overline{\mathbf{c}}, \bar{\gamma}=\mathbf{3} \overline{\mathbf{a}}-\mathbf{7} \overline{\mathbf{c}}\) అయితే \(\left[\begin{array}{lll}
\bar{\alpha} & \bar{\beta} & \bar{\gamma}
\end{array}\right]\) ను కనుక్కోండి.
Solution:

Question 11.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతలీయ సదిశలు. \(\left[\begin{array}{lll}
2 \bar{a}-\bar{b}+3 \bar{c}, & \bar{a}+\bar{b}-2 \bar{c}, & \bar{a}+\bar{b}-3 \bar{c}]
\end{array}\right.\) = \(\lambda[\overline{\mathbf{a}} \overline{\mathbf{b}} \overline{\mathbf{c}}]\) అయితే, λ విలువను కనుక్కోండి.
Solution:

Question 12.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతలీయ సదిశలు. \([\overline{\mathbf{a}}+2 \overline{\mathbf{b}} \quad 2 \overline{\mathbf{b}}+\overline{\mathbf{c}} 5 \bar{c}+\overline{\mathbf{a}}]=\lambda[\bar{a} \overline{\mathbf{b}} \overline{\mathbf{c}}]\) అయితే, λ విలువను కనుక్కోండి.
Solution:

Question 13.
a, b, c లు అతలీయ సదిశలైతే \(\frac{1}{a b c}\) (a + 2b – c) [(a – b) × (a – b – c)] విలువను కనుక్కోండి.
Solution:

Question 14.
\(\bar{a}, \bar{b}, \bar{c}\) లు పరస్పరం లంబంగా ఉండే యూనిట్ సదిశలైతే \([\bar{a}, \bar{b}, \bar{c}]^2\) ను కనుక్కోండి.
Solution:

Question 15.
\(\bar{a}, \bar{b}, \bar{c}\) లు శూన్యేతర సదిశలు, \(\overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు రెండింటికి \(\overline{\mathbf{a}}\) సదిశ లంబంగా ఉంటుంది. \(|\bar{a}|=2,|\bar{b}|=3\), \(|\bar{c}|=4,(\bar{b}, \bar{c})=\frac{2 \pi}{3}\) అయితే, \(|[\bar{a} \bar{b} \bar{c}]|\) ను కనుక్కోండి. [May ’08]
Solution:

Question 16
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు సతలీయ యూనిట్ సదిశలైతే, \(\left[\begin{array}{lll}
2 \bar{a}-\bar{b} & 2 \bar{b}-\bar{c} & 2 \bar{c}-\bar{a}
\end{array}\right]\) ను కనుక్కోండి.
Solution:

II.

Question 1.
\(\left[\begin{array}{lll}
\bar{b} & \bar{c} & \bar{d}
\end{array}\right]+\left[\begin{array}{lll}
\bar{c} & \bar{a} & \bar{d}
\end{array}\right]+\left[\begin{array}{lll}
\bar{a} & \bar{b} & \bar{d}
\end{array}\right]\) = \(\left[\begin{array}{lll}
\bar{a} & \overline{\mathbf{b}} & \overline{\mathbf{c}}
\end{array}\right]\) అయితే \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}, \overline{\mathbf{d}}\) లు స్దాన సదిశలుగా గల బిందువులు సతలీయాలని చూపండి.
Solution:

Question 2.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతలీయ సదిశలైతే \(2 \overline{\mathbf{a}}+\mathbf{3} \overline{\mathbf{b}}-\overline{\mathbf{c}}\), \(\bar{a}-2 \bar{b}+3 \bar{c}, 3 \bar{a}+4 \bar{b}-2 \bar{c}, \bar{a}-6 \bar{b}+6 \bar{c}\) లు స్థాన సదిశలుగా గల నాలుగు బిందువులు సతలీయాలని చూపండి.
Solution:

Question 3.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు శూన్యేతర, సరేఖీయాలు కాని సదిశలు, θ ≠ 0, \(\overline{\mathbf{b}}, \overline{\mathbf{c}}\) ల మధ్య కోణం θ, \(\mid(\overline{\mathbf{a}} \times \overline{\mathbf{b}}) \times \overline{\mathbf{c}}\) = \(\frac{1}{3}|\bar{b} \| \bar{c}||\bar{a}|\) అయితే, sin θ విలువను కనుక్కోండి.
Solution:

Question 4.
(1, 2, 1) (3, 2, 5), (2, -1, 0), (-1, 0, 1) శీర్షాలుగా గల చతుర్ముఖి ఘనపరిమాణాన్ని కనుక్కోండి. [(T.S) Mar. ’15; May ’07]
Solution:
సాధన. ‘O’ మూలబిందువు.
A, B, C, D లు చతుర్ముఖి శీర్షాలు.

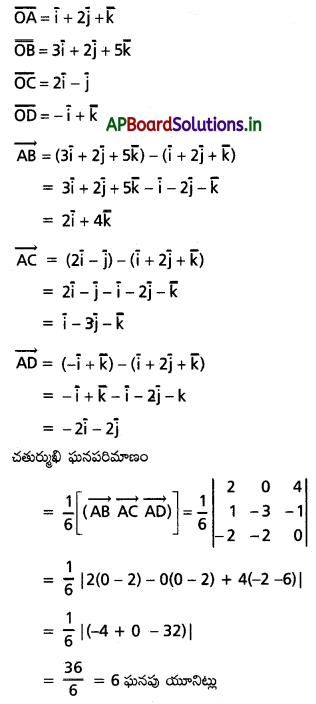
Question 5.
\((\overline{\mathbf{a}}+\overline{\mathbf{b}}) \cdot(\overline{\mathbf{b}}+\overline{\mathbf{c}}) \times(\overline{\mathbf{c}}+\overline{\mathbf{a}})=2[\bar{a} \bar{b} \bar{c}]\) అని చూపండి.
Solution:

Question 6.
\(3 \bar{i}-5 \bar{j}+-\bar{k},-\bar{i}+5 \bar{j}+7 \bar{k}\) సదిశలుగా గల బిందువుల గుండా పోతూ, \(\mathbf{3} \overline{\mathbf{i}}-\overline{\mathbf{j}}+\mathbf{7} \overline{\mathbf{k}}\) సదిశకు సమాంతరంగా ఉండే తలం సమీకరణం 3x + 2y – 2 = 0 అని చూపండి.
Solution:

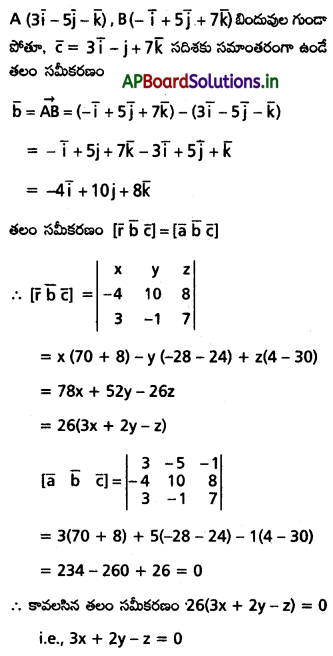
Question 7.
\(\overline{\mathbf{a}} \times[\bar{a} \times(\bar{a} \times \bar{b})]=(\bar{a} \cdot \bar{a})(\bar{b} \times \bar{a})\) అని రుజువు చేయండి.
Solution:

Question 8.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}, \overline{\mathbf{d}}\) లు సతలీయ సదిశలైతే \((\bar{a} \times \bar{b}) \times(\bar{c} \times \bar{d})=0\) అని చూపండి.
Solution:

Question 9.
\([(\bar{a} \times \bar{b}) \times(\bar{a} \times \bar{c})] \cdot \bar{d}=(\bar{a} \cdot \bar{d})[\bar{a} \bar{b} \bar{c}]\) అని చూపండి.
Solution:

Question 10.
\(\overline{\mathrm{a}} \cdot[(\overline{\mathrm{b}}+\overline{\mathrm{c}}) \times(\overline{\mathrm{a}}+\overline{\mathrm{b}}+\overline{\mathrm{c}})]=0\) అని చూపండి.
Solution:

Question 11.
A(3, 2, 1), B(4, λ, 5), C(4, 2, -2),D(6, 5, -1) బిందువులు సతలీయాలైతే λ ను కనుక్కోండి.
Solution:
‘O’ మూలబిందువు.

⇒ 1(0 + 9) – (λ – 2) (-2 + 9) + 4(3 – 0) = 0
⇒ 9 – (λ – 2) (7) + 12 = 0
⇒ 9 – 7λ + 14 + 12 = 0
⇒ 7λ = 35
⇒ λ = 5

Question 12.
\(\bar{r} \cdot(2 \bar{i}+2 \bar{i}-3 \bar{k})=7, \bar{r} \cdot(2 \bar{i}+5 \bar{j}+3 \bar{k})=9\) తలాల ఛేదన రేఖ గుండా, (2, 1, 3) బిందువు గుండా పోయే తలం సదిశా సమీకరణం కనుక్కోండి.
Solution:

Question 13.
(a, b, c) బిందువు గుండా పోతూ \(\overline{\mathrm{r}} \cdot(\overline{\mathrm{i}}+\overline{\mathrm{i}}+\overline{\mathrm{k}})=\mathbf{2}\) తలానికి సమాంతరంగా ఉండే తలం సమీకరణం కనుక్కోండి.
Solution:

Question 14.
\(\bar{r}=6 \bar{i}+2 \bar{j}+2 \bar{k}+\lambda,(\bar{i}-2 \bar{j}+2 \bar{k}), \bar{r}=\) \(-4 \overline{\mathrm{i}}-\overline{\mathrm{k}}+\mu=3 \overline{\mathrm{i}}-2 \overline{\mathrm{i}}-2 \overline{\mathrm{k}}\) రేఖల మధ్య కనిష్ఠ దూరాన్ని కనుక్కోండి.
Solution:

Question 15.
\(\vec{r} \cdot(\bar{i}+\bar{i}+\bar{k})=1,\left(1-4\left(-\frac{1}{2}\right)\right)+4=0\) తలాల ఛేదన రేఖ గుండా, ఇంకా X-అక్షానికి సమాంతరంగా పోయే తలం సమీకరణాన్ని కనుక్కోండి.
Solution:

Question 16.
\(4 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}+\overline{\mathbf{k}},-(\overline{\mathbf{j}}+\overline{\mathbf{k}}), \mathbf{3} \overline{\mathbf{i}}+9 \overline{\mathbf{j}}+4 \overline{\mathbf{k}}\), \(-4 \overline{\mathbf{i}}+4 \overline{\mathbf{j}}+4 \overline{\mathbf{k}}\) సదిశలను స్థానసదిశలుగా గల బిందువులు సతలీయాలని చూపండి.
Solution:
‘O’ మూలబిందువు.
A, B, C, D లు దత్త బిందువులు.

Question 17.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు అతిలీయాలైతే \(\overline{\mathbf{a}}-\overline{\mathbf{b}}, \overline{\mathbf{b}}+\overline{\mathbf{c}}, \overline{\mathbf{c}}+\overline{\mathbf{a}}\) సదిశలు సతలీయాలవుతాయని రుజువు చేయండి.
Solution:

Question 18.
A, B, C బిందువుల స్థాన సదిశలు వరుసగా \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) అయితే, \(\overline{\mathbf{a}} \times \overline{\mathbf{b}}+\overline{\mathbf{b}} \times \overline{\mathbf{c}}+\overline{\mathbf{c}} \times \overline{\mathbf{a}}\) సదిశ ∆ABC తలానికి లంబంగా ఉంటుందని రుజువు చేయండి.
Solution:

III.

Question 1.
\((\bar{a} \times(\bar{b} \times \bar{c})) \times \bar{c}=(\bar{a} \cdot \bar{c})(\bar{b} \times \bar{c})\), \((\overline{\mathbf{a}} \times \overline{\mathbf{b}}) \cdot(\overline{\mathbf{a}} \times \overline{\mathbf{c}})+(\overline{\mathbf{a}} \cdot \overline{\mathbf{b}})(\overline{\mathbf{a}} \cdot \overline{\mathbf{c}})\) = \((\bar{a} \cdot \bar{a})(\bar{b} \cdot \bar{c})\) అని చూపండి.
Solution:

Question 2.
A = (1, -2, -1), B = (4, 0, -3), C = (1, 2, -1), D = (2, -4, -5), బిందువులైతే AB, CD రేఖల మధ్య దూరాన్ని కనుక్కోండి. [Mar. ’14]
Solution:

Question 3.
\(\overline{\mathrm{a}}=\overline{\mathrm{i}}-2 \overline{\mathrm{j}}+\overline{\mathrm{k}}\), \(\overline{\mathrm{b}}=2 \overline{\mathrm{i}}+\overline{\mathrm{j}}+\overline{\mathrm{k}}\), \(\overline{\mathrm{c}}=\overline{\mathrm{i}}+2 \overline{\mathrm{j}}-\overline{\mathrm{k}}\) సదిశలైతే \(\overline{\mathbf{a}} \times(\overline{\mathbf{b}} \times \overline{\mathbf{c}}),|(\overline{\mathbf{a}} \times \overline{\mathbf{b}}) \times \overline{\mathbf{c}}|\) లను కనుక్కోండి.
Solution:

Question 4.
\(\overline{\mathbf{a}}=\overline{\mathbf{i}}-\mathbf{2 j}-\mathbf{j} \overline{\mathbf{k}}, \overline{\mathbf{b}}=\mathbf{2} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}\), \(\overline{\mathbf{c}}=\overline{\mathbf{i}}+3 \overline{\mathbf{j}}-2 \overline{\mathbf{k}}\) సదిశలకు \(\overline{\mathbf{a}} \times(\overline{\mathbf{b}} \times \overline{\mathbf{c}}) \neq(\overline{\mathbf{a}} \times \overline{\mathbf{b}}) \times \overline{\mathbf{c}}\) అని సరిచూడండి. [May ’11; Mar, ’08]
Solution:

Question 5.
\(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\mathbf{3} \overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}-2 \overline{\mathbf{j}}+\overline{\mathbf{k}}\), \(\overline{\mathbf{c}}=-\overline{\mathbf{i}}+\overline{\mathbf{j}}-4 \overline{\mathbf{k}}, \overline{\mathbf{d}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}\), అయితే \(\| \bar{a} \times \bar{b}) \times(\bar{c} \times \bar{d}) \mid\) ను గణన చేయండి. [(T.S) Mar. ’15]
Solution:

Question 6.
A = (1, a, a²), B = (1, b, b²), C = (1, c, c²) సదిశలు అతలీయాలై \(\left|\begin{array}{ccc}
a & a^2 & 1+a^3 \\
b & b^2 & 1+b^3 \\
c & c^2 & 1+c^3
\end{array}\right|\) = 0 అయితే, abc + 1 = 0 అని చూపండి.
Solution:

Question 7.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) శూన్యేతర సదిశలైతే, \(|(\overline{\mathrm{a}} \times \overline{\mathrm{b}} \cdot \overline{\mathrm{c}})|=|\overline{\mathrm{a}}| \overline{\mathrm{b}}|| \bar{c} \mid\) ⇔ \(\overline{\mathbf{a}} \cdot \overline{\mathbf{b}}=\overline{\mathbf{b}} \cdot \overline{\mathbf{c}}=\overline{\mathbf{c}} \cdot \overline{\mathbf{a}}=\mathbf{0}\) అని చూపండి.
Solution:

Question 8.
\(\overline{\mathbf{a}}=\overline{\mathbf{i}}-2 \overline{\mathbf{j}}+3 \overline{\mathbf{k}}, \overline{\mathbf{b}}=2 \overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}\), \(\overline{\mathbf{c}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+2 \overline{\mathbf{k}}\) అయితే \(|(\mathbf{a} \times \overline{\mathbf{b}}) \times \overline{\mathbf{c}}|\), \(|\overline{\mathbf{a}} \times(\overline{\mathbf{b}} \times \overline{\mathbf{c}})|\) లు కనుక్కోండి.
Solution:

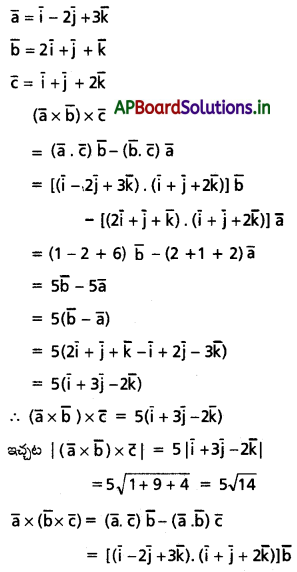
Question 9.
\(|\bar{a}|=1,|\bar{b}|=1,|\bar{c}|=2\), \(\overline{\mathbf{a}} \times(\overline{\mathbf{a}} \times \overline{\mathbf{c}})+\overline{\mathbf{b}}=\mathbf{0}\) అయితే \(\overline{\mathbf{a}}, \overline{\mathbf{c}}\) ల మధ్య కోణాన్ని కనుక్కోండి.
Solution:

Question 10.
\(\overline{\mathbf{a}}=\overline{\mathbf{i}}-\overline{\mathbf{k}}, \quad \overline{\mathbf{b}}=\mathbf{x} \overline{\mathbf{i}}+\overline{\mathbf{j}}+(1-x) \overline{\mathbf{k}}\), \(\bar{c}=y \bar{i}+x \bar{j}+(1+x-y) \bar{k}\) అయితే \(\left[\begin{array}{lll}
\bar{a} & \bar{b} & \bar{c}
\end{array}\right]\) విలువ x, y రెండింటిమీద ఆధారపడదని చూపండి.
Solution:

Question 11.
\(\overline{\mathbf{b}}=\mathbf{2} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}, \overline{\mathbf{c}}=\overline{\mathbf{j}}+\mathbf{3} \overline{\mathbf{k}} \cdot \overline{\mathbf{a}}\) యూనిట్ సదిశ అయితే \(\left[\begin{array}{lll}
\bar{a} & \overline{\mathbf{b}} & \bar{c}
\end{array}\right]\) గరిష్ట విలువను కనుక్కోండి.
Solution:

Question 12.
\(\overline{\mathbf{a}}=\overline{\mathbf{i}}-\overline{\mathbf{j}}, \overline{\mathbf{b}}=\overline{\mathbf{j}}-\overline{\mathbf{k}}, \overline{\mathbf{c}}=\overline{\mathbf{k}}-\overline{\mathbf{i}}\) యూనిట్ సదిశ \(\overline{\mathbf{d}}\) ని \(\overline{\mathbf{a}} \cdot \overline{\mathbf{d}}=\mathbf{0}=[\overline{\mathbf{b}} \overline{\mathbf{c}} \overline{\mathbf{d}}]\) అయ్యేలా కనుక్కోండి.
Solution: