AP Inter 1st Year Maths 1A Solutions Chapter 9 అతిపరావలయ ప్రమేయాలు Ex 9(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 9 అతిపరావలయ ప్రమేయాలు Exercise 9(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 9 అతిపరావలయ ప్రమేయాలు Exercise 9(a)

Question 1.
sinh x = \(\frac{3}{4}\) అయితే cosh (2x), sinh (2x) విలువలు కనుక్కోండి. [Mar. ’14, ’12]
Solution:

Question 2.
sinh x = 3 అయినప్పుడు x = log_e(3 + √10) అని చూపండి.
Solution:

Question 3.
(i) tanh (x – y) = \(\frac{\tanh x-\tanh y}{1-\tanh x \tanh y}\)
Solution:

(ii) coth (x – y) = \(\frac{{coth} x \cdot {coth} y-1}{{coth} y-{coth} x}\) అని నిరూపించండి.
Solution:

Question 4.
ప్రతి n ∈ R కు,
(i) (cosh x – sinh x)ⁿ = cosh (nx) – sinh (nx) [(T.S) Mar. ’15, ’07, ’06]
Solution:

(ii) (cosh x + sinh x)ⁿ = cosh (nx) + sinh (nx) అని నిరూపించండి.
Solution:

Question 5.
x ≠ 0 అయితే \(\frac{\tanh x}{{sech} x-1}+\frac{\tanh x}{{sech} x+1}\) = -2 cosech x నిరూపించండి.
Solution:

Question 6.
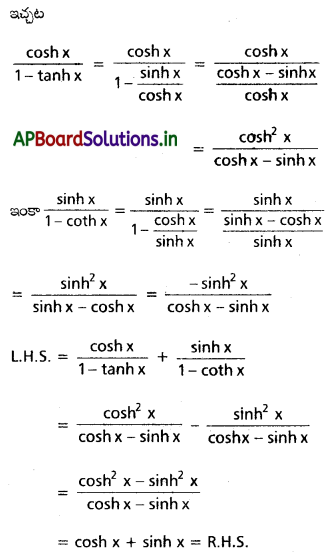
x ≠ 0 అయితే \(\frac{\cosh x}{1-\tanh x}+\frac{\sinh x}{1-{coth} x}\) = sinh x + cosh x అని నిరూపించండి.
Solution:

Question 7.
ప్రతీ x ∈ R కు cosh⁴x – sinh⁴x = cosh (2x) అని నిరూపించండి.
Solution:
LH.S. = cosh⁴x – sinh⁴x
= (cosh²x)² – (sinh²x)²
= [cosh²x – sinh²x] [cosh²x + sinh²x]
= (1) cosh (2x)
= cosh (2x)
∴ cosh⁴x – sinh⁴x = cosh (2x)

Question 8.
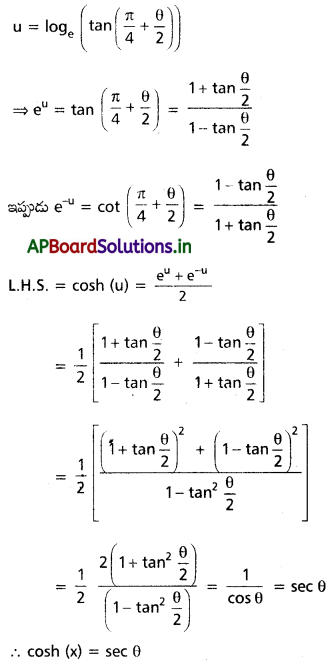
u = \(\log _e\left(\tan \left(\frac{p}{4}+\frac{q}{2}\right)\right)\), cos θ > 0, అయితే cosh u = sec θ అని నిరూపించండి.
Solution: