AP Inter 1st Year Maths 1B Important Questions Chapter 3 సరళరేఖ

Students get through AP Inter 1st Year Maths 1B Important Questions Chapter 3 సరళరేఖ which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1B Important Questions Chapter 3 సరళరేఖ

సాధించిన సమస్యలు

ప్రశ్న 1.
బిందువు (2, 3) గుండా పోతూ నిరూపకాక్షాలతో చేసే శూన్యేతర అంతరఖండాల మొత్తము సున్న అయ్యే సరళరేఖ సమీకరణాన్ని కనుక్కోండి. [Mar. 12]
సాధన:
అంతరఖండ రూపంలో రేఖ సమీకరణము
\(\frac{x}{a}+\frac{y}{b}\) = 1
b = -a అని ఇవ్వబడింది.
రేఖ సమీకరణము
\(\frac{x}{a}-\frac{y}{b}\) = 1 ⇒ x – y = a
ఈ రేఖ (2, 3) గుండా పోతుంది.
2 -3 = a ⇒ a = -1
రేఖ సమీకరణము
x – y = – 1 లేదా x – y + 1 = 0

ప్రశ్న 2.
(at₁², 2at₁), (at₂², 2at₂) బిందువుల ద్వారా పోయే సరళరేఖ సమీకరణాన్ని కనుక్కోండి. [Mar. ’14]
సాధన:
దత్త బిందువుల గుండా పోయే రేఖ సమీకరణము
(x – x₁) (y₁ – y₂) = (y – y₁) (x₁ – x₂)
(x – at₁) (2at₁ – 2at₂)
= (y – 2at₁) (at₁² – at₂²)
(x – at₁²) . 2a(t₁ – t₂) = (y – 2at₁=) a. (t₁² – t₂²)
2x -2at₁² = y(t₁ + t₂) – 2at₁² – 2at₁t₁
2x – (t₁ + t₂)y + 2at₁t₂ = 0

ప్రశ్న 3.
A (- 1, 3) బిందువు గుండా పోతూ B(2, – 5), C(4, 6) బిందువులగుండా పోయే సరళరేఖకు i) సమాంతరంగా, ii) లంబంగా ఉండే సరళరేఖ సమీకరణం కనుక్కోండి. [May 11]
సాధన:
BC వాలు = \(\frac{-5-6}{2-4}=\frac{-11}{-2}=\frac{11}{2}\)

i) కావలసిన రేఖ BC కి సమాంతరము మరియు A(-1, 3)
గుండా పోతుంది.
సమాంతర రేఖ సమీకరణము
y – 3 = \(\frac{11}{2}\) (x + 1)
2y-6= = 11x + 11
11x – 2y + 17= 0

ii) దత్త రేఖ BC కి లంబంగా ఉంది.
ఈ రేఖ వాలు = – \(\frac{1}{m}\) = –\(\frac{2}{11}\)
ఈ రేఖ A (-1, 3) గుండా పోతుంది. కావలసిన రేఖ సమీకరణము
y – 3 = –\(\frac{2}{11}\) (x + 1)
11y – 33 = -2x – 2
2x + 11y – 31 = 0

ప్రశ్న 4.
(1, 11), (2, 15), (-3, -5) బిందువులు సరేఖీయాలని చూపండి. ఈ బిందువుల గుండా పోయే సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
(1, 11), B(2, 15), C (-3, -5) లు దత్త బిందువులు.
AB సమీకరణము
(y – y₁) (x₁ – x₂) = (x – x₁) (y₁ – y₂)
(y – 11) (1 – 2) = (x – 1) (11 – 15)
– (y – 11) = – 4 (x – 1)
– y + 11 = – 4x + 4
4x – y + 7 = 0
C నిరూపకాలు (-3, -5)
4x – y + 7 = 4(−3) + 5 + 7
-12 + 12 = 0
C బిందువు AB మీద ఉంది.
A, B, C లు సరేఖీయాలు,
ఈ బిందువుల గుండా పోయే రేఖ సమీకరణము
4x – y + 7 = 0

ప్రశ్న 5.
ఒక సరళరేఖ A(1, 2) గుండా పోతూ X- అక్షం ధన దిశతో అపసవ్య దిశలో tan^-1\(\frac{4}{3}\) కోణం చేస్తుంది. ఆ సరళరేఖపై A నుంచి 5 యూనిట్ల దూరంలోగల బిందువులను కనుక్కోండి.
సాధన:

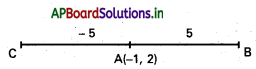
దత్తాంశం α = tan^-1\(\frac{4}{3}\) ⇒ tan α = \(\frac{4}{3}\)

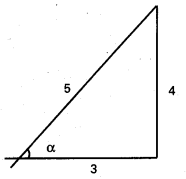
cos α = \(\frac{3}{5}\)
sin α = \(\frac{4}{5}\)
(x₁, y₁) = (1, -2) = x₁ = 1, y₁ = -2
సందర్భం : i) r = 5
x = x₁ + r cos α = 1 – 5. \(\frac{3}{5}\) = 1 + 3 = 4
y = y₁ + r sin α = – 2 + 5. \(\frac{4}{5}\) = -2 + 4 = 2
B నిరూపకాలు (4, 2)

సందర్భం : ii) r = -5
x = x₁ + r cos α = 1 – 5. \(\frac{3}{5}\) = 1 – 3 = -2
y = y₁ + r sin α = -2 – 5 . \(\frac{4}{5}\) = -2 – 4 = -6
C నిరూపకాలు (- 2, – 6)

ప్రశ్న 6.
రేఖ y = \(\sqrt{3}\)x కు సమాంతరంగా ఉంటూ Q(2, 3) గుండా పోయే ఒక సరళరేఖ, 2x + 4y – 27 = 0 రేఖను P వద్ద ఖండిస్తుంది. PQ దూరాన్ని కనుక్కోండి.
సాధన:
PQ రేఖ y = \(\sqrt{3}\)xకు సమాంతరము.
tan α = \(\sqrt{3}\) = tan 60°
α = 60°
Q(2, 3) దత్త బిందువు.

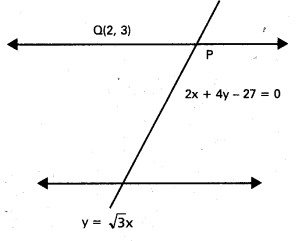
ఏదేని బిందువు P నిరూపకాలు
(x₁ +r cos α, y₁ + r sin α)
(2 + r cos 60°, 3 + r sin 60°)
P (2 + \(\frac{r}{2}\), 3 + \(\frac{\sqrt{3}}{2}\) r)
P బిందువు 2x + 4y – 27 = 0 రేఖ మీద ఉంది.
2 \(\left(2+\frac{r}{2}\right)\) + 4 \(\left(3+\frac{\sqrt{3}}{2} r\right)\) – 27 = 0
4 + r + 12 + 2\(\sqrt{3}\)r – 27 = 0
r(2\(\sqrt{3}\) + 1) = 27 – 6 = 11
r = \(\frac{11}{2 \sqrt{3}+1} \cdot \frac{2 \sqrt{3}-1}{2 \sqrt{3}-1}\)
= \(\frac{11(2 \sqrt{3}-1)}{11}\)
PQ = |r| = 2\(\sqrt{3}\) – 1

ప్రశ్న 7.
3x + 4y + 12 = 0 సమీకరణాన్ని
i) వాలు – అంతరఖండ రూపం
ii) అంతరఖండ రూపం
iii) అభిలంబరూపంలోకి మార్చండి.
సాధన:
దత్త సమీకరణము 3x + 4y + 12 = 0
i) వాలు – అంతరఖండ రూపము :
4y = -3x – 12
y = \(\left(-\frac{3}{4}\right)\)x + (-3)
వాలు = –\(\frac{3}{4}\), y – అంతరఖండము = – 3.

ii) అంతరఖండ రూపము :
-3x – 4y = 12
–\(\frac{3 x}{12}-\frac{4 y}{12}\) = 1
\(\frac{x}{(-4)}+\frac{y}{(-3)}\) = 1
x – అంతరఖండము = – 4, y – అంతరఖండము = -3

iii) అభిలంబ రూపము :
-3x – 4y = 12
\(\sqrt{9+16}\) = 5 తో భాగించగా
\(\left(-\frac{3}{5}\right) x+\left(-\frac{4}{5}\right) y=\frac{12}{5}\)
cos α = \(\frac{-3}{5}\), sin α = – \(\frac{4}{5}\) అనుకుంటే
p = \(\frac{12}{5}\)
x cos α + y sin α = p
α మూడవ పాదంలో కోణం అనుకొంటే
α = л + tan^-1 \(\left(\frac{4}{3}\right)\)

ప్రశ్న 8.
x = 0, y = 0, 3x + 4y = a (a > 0) సరళరేఖలతో ఏర్పడే త్రిభుజవైశాల్యం 6 అయితే, a విలువ కనుక్కోండి. [May ’11]
సాధన:
రేఖ సమీకరణము 3x + 4y = a
\(\frac{3 x}{a}+\frac{4 y}{a}\) = 1
\(\frac{x}{\left(\frac{a}{3}\right)}+\frac{y}{\left(\frac{a}{4}\right)}\) = 1
OA = x – అంతరఖండము = \(\frac{a}{3}\),
OB = y – అంతరఖండము = \(\frac{a}{4}\)
∆ OAB = \(\frac{1}{2}\) |OA . OB|
= \(\frac{1}{2}\left|\frac{a}{3} \cdot \frac{a}{4}\right|=\frac{a^2}{24}\)
\(\frac{a^2}{2 a}\) = 6 ⇒ a² = 144
a = ± 12
a > 0 కనుక
∴ a = 12

ప్రశ్న 9.
2x – 3y + k = 0, 3x – 4y – 13 = 0, 8x – 11y – 33 = 0 రేఖలు అనుషక్తాలయితే k విలువ కనుక్కోండి.
సాధన:
L₁, L₂, L₃ లు దత్తరేఖల సమీకరణాలు
2x – 3y + k = 0 ……………….. (1)
3x – 4y – 13 = 0 ………………. (2)
8x – 11y – 33 = 0 ………………… (3)
(2), (3) లను సాధించగా

x = 11, y = 5
(2), (3) ల ఖండన బిందువు (11, 5)
దత్త రేఖలు L., L2, L, అనుషక్తాలు.
∴ L₁ చాపం (11, 5) బిందువు మీద ఉంది.
∴ 2(11) – 3(5) + k = 0
k = -7

ప్రశ్న 10.
ax + by + c = 0, bx + cy + a = 0, cx + ay + b = 0 సరళరేఖలు అనుశక్తాలయితే a³ + b³ + c³ = 3abc అని చూపండి.
సాధన:
దత్త రేఖల సమీకరణాలు
ax + by + c = 0 …………….. (1)
bx + cy + a = 0 ……………. (2)
cx + ay + b = 0 …………… (3)
(1), (2) లను సాధించగా ఖండన బిందువు

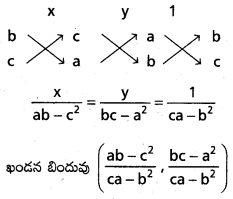
P బిందువు cx + y + b = 0 మీద ఉంది.
c\(\left(\frac{a b-c^2}{c a-b^2}\right)\) + a\(\left(\frac{b c-a^2}{c a-b^2}\right)\) + b = 0
c(ab – c²) + a (bc – a²) + b(ca – b²) = 0
abc – c³ + abc – a³ + abc – b³ = 0
∴ a³ + b³ + c³ = 3abc.

ప్రశ్న 11.
\(\frac{x}{a}+\frac{y}{b}\) = 1, \(\frac{x}{b}+\frac{y}{a}\) = 1 సరళరేఖల ఖందన బిందువు గుండా పోయే ఒక చల సరళరేఖ నిరూపకాక్షాలను A, B లలో ఖండిస్తోంది. \(\overline{\mathrm{A B}}\) మధ్య బిందువు బిందుపథ సమీకరణం 2(a + b) xy = ab(x + y) అని చూపండి.
సాధన:
దత్తరేఖల సమీకరణాలు
\(\frac{x}{a}+\frac{y}{b}\) = 1
మరియు \(\frac{x}{b}+\frac{y}{a}\) = 1
సాధించగా ఖండన బిందువు
P నిరూపకాలు \(\left(\frac{a b}{a+b}, \frac{a b}{a+b}\right)\)
Q (x_o, y_o) బిందుపథం మీది ఏదేని బిందువు
⇔ x – అంతరఖండం 2x_o, y – అంతరఖండం 2y_o గల
⇔ P బిందువు \(\frac{x}{2 x_0}+\frac{y}{2 y_0}\) = 1 రేఖ మీద ఉంది.
.i.e., \(\frac{a b}{a+b}\left(\frac{1}{2 x_0}+\frac{1}{2 y_0}\right)\) = 1
⇒ \(\frac{a b}{a+b} \cdot \frac{x_0+y_0}{2 x_0 y_0}\) = 0
ab(x_o + y_o) = 2(a + b) x_o y_o
Q(x_o, y_o) బిందువు వక్రం మీద ఉంది.
2(a + b)xy = ab(x + y)
AB మధ్య బిందుపథము 2(a + b)xy = ab(x + y)

ప్రశ్న 12.
a, b, c లు అంకశ్రేఢిలో ఉంటే ax + by + c = 0 సమీకరణం ఒక అనుషక్త రేఖల కుటుంబాన్ని సూచిస్తుందని చూపండి. అనుషక్త బిందువును కూడా కనుక్కోండి.
సాధన:
a, b, c లు AP. లో ఉన్నాయి.
2b = a + c
a – 2b + c = 0
a.1 + b(-2) + c = 0.
ax + by + c = 0 కి లంబరేఖలు (1, -2) స్థిర బిందువు గుండా పోతున్నాయి.
∴ a, b, c లు పరామితులైతే, ax + by + c = 0 సూచించే రేఖలు అనుషక్తాలు.
∴ అనుషక్త బిందువు (1, 2).

ప్రశ్న 13.
4x – y + 7 = 0, kx – 5y – 9 = 0 సరళరేఖల మధ్యకోణం 45° అయితే k విలువను కనుక్కోండి.
సాధన:

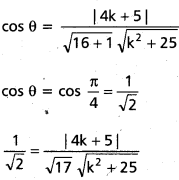
వర్గీకరించి అడ్డగుణకారము చేయగా
2(4k + 5)² = 17(k² + 25)
2(16k² + 40k + 25) = 17k² + 425
32k² + 80k + 50 = 17k² + 425
15k² + 80k – 375 = 0
3k² + 16k – 75 = 0
(k – 3) (3k + 25) = 0
k = 3 లేదా -25/3

ప్రశ్న 14.
(x_o, y_o) బిందువు గుండా పోతూ ax + by + c = 0 సరళరేఖకు (i) సమాంతరంగా ii) లంబంగా ఉండే సరళరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
దత్తరేఖ సమీకరణముax + by + c = 0
i) సమాంతర రేఖ సమీకరణము ax + by = k …………….. (1)
ఈ రేఖ P(x_o, y_o) గుండా పోతుంది.
ax_o + by_o = k ……………… (2)
(1) నుండి (2) తీసివేయగా కావలసిన రేఖ సమీకరణము
a(x – x_o) + b(y – y_o) = 0

ii) లంబంగా ఉండే రేఖ సమీకరణము
bx – ay = k
ఈ రేఖ P(x_o, y_o) గుండా పోతుంది.
⇒ bx_o – ay_o = k
తీసివేయగా, కావలసిన రేఖ సమీకరణము
b(x – x_o) – a(y – y_o) = 0

ప్రశ్న 15.
5x – 2y = 7 రేఖకు లంబంగా ఉంటూ 2x + 3y = 1, 3x + 4y = 6 రేఖల ఖండన బిందువు గుండా పోయే సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
దత్తరేఖలు L₁ = 2x + 3y – 1 = 0
L₂ = 3x + 4y – 6 = 0
L₁ = 0, L₂ = 0 ల ఖండన బిందువు గుండా పోయే రేఖ సమీకరణము
L₁ + kL₂
(2x + 3y – 1) + k(3x + 4y – 6) = 0
(2 + 3k)x + (3 + 4k)y – (1 + 6k) = 0 ……………… (1)
ఈ రేఖ 5x – 2y = 7 కు లంబము. ……………….. (2)
a₁a₂ + b₁b₂ = 0
5(2 + 3k) – 2(3 + 4k) = 0
10 + 15k – 6 – 8k = 0
7k = – 4 ⇒ k = – 4/7
(1) లో ప్రతిక్షేపిస్తే కావలసిన రేఖ సమీకరణము
(2 – \(\frac{12}{7}\))x + (3 – \(\frac{16}{7}\))x – (1 – \(\frac{24}{7}\)) = 0
\(\frac{2}{7}\)x + \(\frac{5}{7}\)y + \(\frac{17}{7}\) = 0
⇒ 2x + 5y + 17 = 0

ప్రశ్న 16.
(3, – 4), (a, B) లను కలిపే రేఖాఖండాన్ని రేఖ 2x – 3y – 5 = 0 లంబ సమద్విఖండన చేస్తే α + β విలువ కనుక్కోండి.
సాధన:
(α, β) అనేది
2x – 3y – 5 = 0 రేఖ దృష్ట్యా (3, -4) ప్రతిబింబం (α, β).
\(\frac{\alpha-3}{2}=\frac{\beta+4}{-3}=\frac{-2(6+12-5)}{4+9}\) = -2
α – 3 = – 4 ⇒ a = -1
β + 4 = 6 ⇒ β = 2
α + β = 1 + 2 = 1

ప్రశ్న 17.
ax + by + p = 0, ax + by + q = 0, cx + dy + r = 0, cx + dy + s = 0 అనే నాలుగు సరళరేఖలు ఒక సమాంతర చతుర్భుజాన్ని ఏర్పరిస్తే ఆ విధంగా ఏర్పడే సమాంతర చతుర్భుజం వైశాల్యం \(\left|\frac{(p-q)(r-s)}{b c-a d}\right|\) అని చూపండి.
సాధన:
L₁, L₂, L₃, L₄ లు రేఖల సమీకరణాలు
L₁ ≡ ax + by + p = 0;
L₂ ≡ ax + by + q = 0
L₃ ≡ cx + dy + r = 0.
L₄ ≡ cx + dy + s = 0
L₁, L₂ లు సమాంతరాలు. L₃, L₄ లు సమాంతరాలు.

ప్రశ్న 18.
ఒక లంబకోణ సమద్విబాహు త్రిభుజం యొక్క కర్ణం చివరి బిందువులు (1, 3), (−4, 1). ఆ త్రిభుజం యొక్క లంబ భుజాల సమీకరణాలను కనుక్కోండి.
సాధన:
A (1, 3), B = (-4, 1) అని \(\overline{A B}\) కర్ణంగా కలిగిన లంబకోణ సమద్విబాహు త్రిభుజాన్ని ABC అని అనుకుంటే,
\(\stackrel{\leftrightarrow}{A C}, \stackrel{\leftrightarrow}{B C}\) ల సమీకరణాలను కనుక్కోవాలి.
\(\overleftrightarrow{A B}\) యొక్క వాలు’ = \(\frac{1-3}{-4-1}=\frac{2}{5}\) కాబట్టి \(\overleftrightarrow{A C}, \stackrel{\leftrightarrow}{B C}\) లు ఊర్ద్వ రేఖలు కావు.
\(\overleftrightarrow{A C}\) యొక్క వాలును m అనుకొంటే,

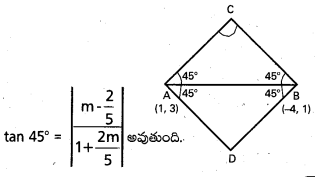
⇒ \(\frac{5 m-2}{5+2 m}\) ± 1
⇒ m = \(\frac{7}{3}\) లేదా \(\frac{-3}{7}\)
\(\overleftrightarrow{A C}\) వాలును \(\frac{7}{3}\) అనుకొంటే, \(\overleftrightarrow{B C}\) వాలు
\(\frac{-3}{7}\) అవుతుంది.
\(\overleftrightarrow{A C}\), \(\overleftrightarrow{B C}\) సమీకరణాలు వరసగా
y – 3 = \(\frac{7}{3}\) (x – 1), y – 1 = –\(\frac{3}{7}\) (x + 4).
ఇవి వరసగా 7x – 3y + 2 = 0, 3x + 7y + 5 = 0 అవుతాయి.
AB గుండా \(\overleftrightarrow{B C}\), \(\overleftrightarrow{A C}\) లకు సమాంతరంగా గీసిన సరళరేఖలు D వద్ద ఖండించుకొంటే, ∆ABD కూడా \(\overline{\mathrm{AB}}\) కర్ణంగా గల లంబకోణ సమద్విబాహు త్రిభుజం అవుతుంది.
\(\overleftrightarrow{A D}\), \(\overleftrightarrow{B D}\) ల సమీకరణాలు వరసగా
3(x – 1) + 7(y – 3) = 0, 7(x + 4) – 3(y – 1) = 0 లు
అంటే 3x + 7y − 24 = 0, 7x – 3y + 31 = 0.
∴ కావలసిన లంబభుజాల సమీకరణాలు
7x – 3y + 2 = 0, 3x + 7y + 5 = 0
లేదా 3x + 7y – 24 = 0, 7x – 3y + 31 = 0.
గమనిక : ADBC ఒక చతురస్రమవుతుంది.

ప్రశ్న 19.
ఒక సరళరేఖ 5x + y + 4 = 0, 3x + 4y – 4 = 0 అనే సరళరేఖల మధ్య చేసే అంతర ఖండం యొక్క మధ్య బిందువు (1, 5) అయితే, ఆ సరళ రేఖా సమీకరణాన్ని కనుక్కోండి.
సాధన:
కావలసిన సరళరేఖ 3x + 4y – 4 = 0 ను A వద్ద 5x y + 4 = 0 ను B వద్ద ఖండిస్తుందనుకొందాం. అప్పుడు ఇచ్చిన
సరళరేఖల మధ్య ఉన్న అంతర ఖండం \(\overleftrightarrow{A B}\) అవుతుంది.
\(\overleftrightarrow{A B}\) మధ్య బిందువును C అనుకొంటే C = (1, 5) అవుతుంది.
5x – y + 4 = 0 ను y = 5x + 4 గా రాయవచ్చు. కాబట్టి \(\overleftrightarrow{B X}\) మీద ఏదైనా బిందువును (t, 5t + 4), (t వాస్తవ సంఖ్యగా) రాయవచ్చు.
కాబట్టి ఏదో ఒక t విలువకు B = (t, 5t + 4) అవుతుంది.
\(\overline{\mathrm{AB}}\) యొక్క మధ్య బిందువు (1, 5) కాబట్టి,
A = [2 – t, 10 – (5t + 4)]
= [2 -t, 6 – 5t] అవుతుంది.
A బిందువు 3x + 4y – 4 = 0 మీద ఉండటం వల్ల,
3(2 – t) + 4(6 – 5t) – 4 = 0 అవుతుంది.
⇒ -23t + 26
⇒ t = \(\frac{26}{23}\)

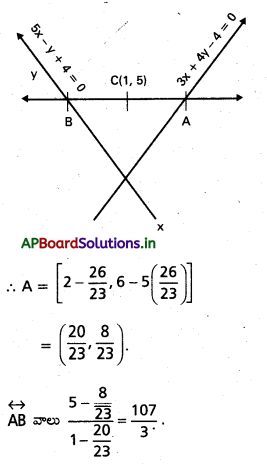
\(\overleftrightarrow{A B}\) సమీకరణం y – 5 = latex]\frac{107}{3}[/latex] (x – 1).
⇒ 3y – 15 = 107x – 107
⇒ 107x – 3y – 92 = 0

ప్రశ్న 20.
ఒక సమబాహు త్రిభుజం యొక్క అంతర కేంద్రం మూల బిందువు వద్ద ఉంది. ఒక భుజం x + y – 2 = 0 మీద ఉంటే ఈ భుజానికెదురుగా నున్న శీర్షాన్ని కనుక్కోండి.
సాధన:
సమబాహు త్రిభుజాన్ని ABC అని, x + y + 2 = 0 మీద
\(\overline{\mathrm{BC}}\) భుజం ఉందనుకొందాం.
ABC త్రిభుజం యొక్క అంతర కేంద్రం మూల బిందువు O కాబట్టి, ∠BAC యొక్క సమద్విఖండన రేఖను \(\overleftrightarrow{A D}\) అనుకొంటే, \(\overleftrightarrow{A D}\) అనేది \(\overleftrightarrow{B C}\) యొక్క లంబ సమద్విఖండన రేఖ అవుతుంది. ∆ABC సమబాహు త్రిభుజం అవడం వల్ల O, కేంద్రభాసం కూడా అవుతుంది. కాబట్టి AO: OD = 2 : 1. కేంద్రభాసం, అంతర కేంద్రం, పరికేంద్రం, లంబకేంద్రాలు ఏకీభవిస్తాయి]
D = (h, k) అనుకొందాం. నుంచి \(\overleftrightarrow{B C}\) మీదకు గల లంబపాదం D, కాబట్టి

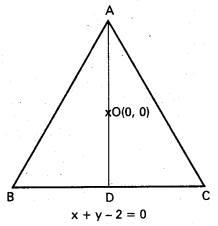
\(\frac{h-0}{1}=\frac{k-0}{1}=\frac{-(-2)}{2}\) = 1
∴ h = 1, k = 1
D = (1, 1).
A = (x₁, y₁) అనుకొంటే, (0,0) = \(\left(\frac{2+x_1}{3}, \frac{2+y_1}{3}\right)\)
∴ x₁ = -2, y₁ = -2.
కావలసిన శీర్షం A = (-2, -2).

ప్రశ్న 21.
(−5, -7), (13, 2), (−5, 6) శీర్షాలుగా గల త్రిభుజం లంబకేంద్రాన్ని కనుక్కోండి.
సాధన:
A(-5, -7), B(13,2), (5, 6) లు త్రిభుజ శీర్షాలు.
A నుండి BC కి లంబం AD
B నుండి AC కి లంబము BE.

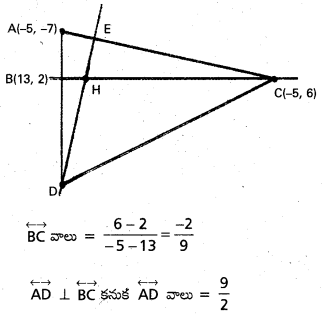
\(\overleftrightarrow{A D}\) సమీకరణము
9x – 2y = 45 + 14 = -31 ……………….. (1)
\(\overleftrightarrow{A C}\) సమీకరణము x = -5 ఇది ఊర్ధ్వరేఖ
\(\overleftrightarrow{B E}\) సమీకరణము y = 2. ……………….. (2)
(1), (2) ల ఖండన బిందువు (−3, 2).
ఇది ∆ ABC లంబకేంద్రము

ప్రశ్న 22.
7x + y – 10 = 0, x – 2y + 5 = 0, x + y + 2 = 0 లు ఒక త్రిభుజం సమీకరణాలైతే త్రిభుజం లంబకేంద్రాన్ని కనుక్కోండి. [T.S Mar. ’15]
సాధన:
∆ ABC దత్త త్రిభుజము
x – 2y + 5 = 0 ……………. (1)
7x + y – 10 = 0 ………………. (2)
x + y + 2 = 0 ……………… (3)

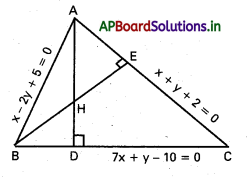
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{B C}\), A, B ల నుండి భుజాల మీదకు గీయబడి ఉన్నాయి.
(1), (3) లను సాధిస్తే A నిరూపకాలు = (-3, 1).
\(\overleftrightarrow{A D}\) ⊥ \(\overleftrightarrow{B C}\) కనుక \(\overleftrightarrow{A D}\) సమీకరణము
x – 7y = -3 – 7 = -10 …………….. (4)
(1), (2) లను సాధించగా B నిరూపకాలు = (1, 3).
\(\overleftrightarrow{B E}\) ⊥ \(\overleftrightarrow{A C}\) కనుక \(\overleftrightarrow{B E}\) సమీకరణము
x – y = 1 – 3 = -2 ………………. (5)
(4), (5) ల ఖండన బిందువు \(\left(\frac{-2}{3}, \frac{4}{3}\right)\)
∆ ABC లంబకేంద్రం.

ప్రశ్న 23.
(1, 3), (–3, 5), (5, -1) లు శీర్షాలుగా గల త్రిభుజం పరికేంద్రం కనుక్కోండి.
సాధన:
త్రిభుజ శీర్షాలు
A(1, 3), B(-3, 5), (5, -1),
\(\overline{\mathrm{BC}}, \overline{\mathrm{CA}}\) ల మధ్య బిందువు D(1, 2), E(3, 1).
\(\overline{\mathrm{BC}}, \overline{\mathrm{CA}}\) ల లంబ సమద్విఖండన రేఖల ఖండన బిందువు S అనుకొనుము.

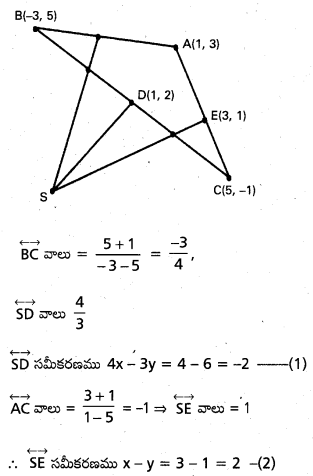
(1), (2) లను సాధిస్తే 5 – (-8, -10) ∆ ABC యొక్క పరికేంద్రం.

ప్రశ్న 24.
3x – y – 5 = 0, x + 2y – 4 = 0, 5x + 3y + 1 = 0 లు భుజాలుగా గల త్రిభుజం పరికేంద్రం కనుక్కోండి. [May ’11, ’05; Mar. ’06]
సాధన:
∆ ABC భుజాలు BC, CA, AD ల సమీకరణాలు వరుసగా
3x – y – 5 = 0, x + 2y – 4 = 0 మరియు 5x + 3y + 1 = 0
రెండేసి సమీకరణాలను తీసుకుని A(-2, 3), B(1, -2), C(2, 1).
\(\overline{\mathrm{BC}}, \overline{\mathrm{CA}}\) ల మధ్య బిందువుల నిరూపకాలు వరుసగా
D = \(\left(\frac{3}{2}, \frac{-1}{2}\right)\), E = (0, 2).

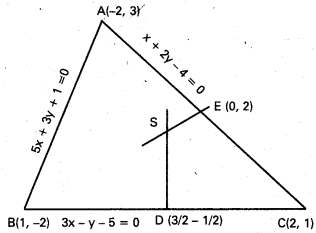
\(\overline{\mathrm{BC}}\) లంబ సమద్విఖండన రేఖ \(\stackrel{\leftrightarrow}{S D}\) సమీకరణము x + 3y = 0, \(\overline{\mathrm{AC}}\) లంబ సమద్విఖండన రేఖ 2x + y + 2 = 0 రేఖ సమీకరణము.
ఈ రెండు సమీకరణాలను సాధిస్తే, S\(\left(\frac{-6}{7}, \frac{2}{7}\right)\)
ఇది ∆ ABC పరికేంద్రము

ప్రశ్న 25.
y = \(\sqrt{3}\)x, y = –\(\sqrt{3}\)x, y = 3 సరళరేఖలతో ఏర్పడే త్రిభుజం అంతర కేంద్రం కనుక్కోండి.
సాధన:

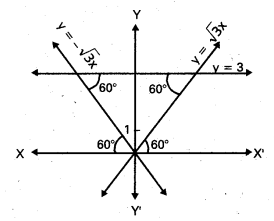
y = \(\sqrt{3}\)x, y = –\(\sqrt{3}\)x రేఖలు X – అక్షంలో వరుసగా 60°, 120° కోణాలు చేస్తున్నాయి.
y = 3 క్షితిజ సమాంతర రేఖ.
ఈ రేఖలతో ఏర్పడే త్రిభుజం పరావలయం
O(0, 0), A(\(\sqrt{3}\), 3), D(-\(\sqrt{3}\), 3) లు సమబాహు త్రిభుజ శీర్షాలు.
∴ అంతర కేంద్రము \(\left(\frac{0+\sqrt{3}-\sqrt{3}}{3}, \frac{0+3+3}{3}\right)\)
= (0, 2).

ప్రశ్న 26.
ఒక సరళరేఖ మూల బిందువు నుంచి 4 యూనిట్ల దూరంలో ఉండి, మూల బిందువు నుంచి ఆ రేఖకు గీసిన అభిలంబ కిరణం x- అక్షం ధన దిశతో 135° కోణం చేస్తే, అ సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
దత్త సరళ రేఖ సమీకరణం x cos αx + y sin α = p
p = 4, α = 135°
అంటే \(x\left(\frac{-1}{\sqrt{2}}\right)+y\left(\frac{1}{\sqrt{2}}\right)\) = 4
లేదా x – y + 4\(\sqrt{2}\) = 0

ప్రశ్న 27.
x + y + 1 = 0 సమీకరణాన్ని అభిలంబ రూపంలోకి మార్చండి. సాధన. x + y + 1 = 0
సాధన:
x + y + 1 = 0
⇔ \(\left(\frac{-1}{\sqrt{2}}\right) x+\left(\frac{-1}{\sqrt{2}}\right) y=\frac{1}{\sqrt{2}}\)
⇔ x cos \(\frac{5 \pi}{4}\) + y sin \(\frac{5 \pi}{4}\) = \(\frac{1}{\sqrt{2}}\)
అందువల్ల దత్త సరళరేఖ సమీకరణానికి అభిలంబ రూపం
x cos \(\frac{5 \pi}{4}\) + y sin \(\frac{5 \pi}{4}\) = \(\frac{1}{\sqrt{2}}\) అని, మూలబిందువు నుంచి ఆ రేఖ దూరం \(\frac{1}{\sqrt{2}}\) అని స్పష్టం.

ప్రశ్న 28.
2x + y + 4 y – 3x = 7 రేఖల మధ్య కోణాన్ని కనుక్కోండి.
సాధన:
దత్తరేఖల మధ్యకోణం = cos^-1 \(\frac{-6+1}{\sqrt{5 \times 10}}\)
= cos^-1\(\left[\frac{5}{\sqrt{2}}\right]\)
= cos^-1 \(\left[\frac{1}{\sqrt{2}}\right]=\frac{\pi}{4}\)

ప్రశ్న 29.
(-1, 3) నుంచి 5x – y – 18 = 0 సరళరేఖ మీదికి లంబపాదం కనుక్కోండి.
సాధన:
(-1, 3) నుంచి 5x – y – 18 = 0 రేఖ మీదికి లంబపాదం (h, k)
⇒ \(\frac{h-(-1)}{5}=\frac{k-3}{-1}=-\frac{(-5-3-18)}{5^2+1^2}\) = 1
⇒ h + 1 = 5, k – 3 = -1
⇒ (h, k) = (4, 2)

ప్రశ్న 30.
3x + 4y – 3 = 0, 6x + 8y – 1 = 0 సమాంతర రేఖల మధ్యదూరం కనుక్కోండి.
సాధన:
దత్త సరళరేఖల సమీకరణాలను 6x + 8y – 6 = 0,
6x + 8y – 1 = 0
ఇప్పుడు \(\frac{\left|c_1-c_2\right|}{\sqrt{a^2+b^2}}\) నుంచి ఈ సమాంతర రేఖల
మధ్యదూరం = \(\frac{-6+1}{\sqrt{6^2+8^2}}=\frac{5}{10}=\frac{1}{2}\)

ప్రశ్న 31.
\(\sqrt{3}\)x + y + 1 = 0, x + 1 = 0 రేఖల మధ్యకోణం కనుక్కోండి.
సాధన:
\(\sqrt{3}\)x + y + 1 = 0 సరళరేఖవాలు – \(\sqrt{3}\) కావడంతో అది x-అక్షంతో 60° కోణం చేస్తుంది. అందువల్ల ఆరేఖ y-అక్షంతో 30° కోణం చేస్తుంది. కాని x + 1 = 0 సమీకరణం ఒక ఊర్ద్వ రేఖను సూచిస్తుంది. కాబట్టి దత్తరేఖల మధ్యకోణం = 30°.

ప్రశ్న 32.
x + y + 1 = 0, 2x – y + 5 = 0 సరళరేఖల ఖండన బిందువు గుండాను (5, -2) బిందువు గుండాను. పోయే సరళరేఖ సమీకరణం కనుక్కోండి.
సాధన:
(5, -2) బిందువు 2x – y + 5 = 0 రేఖ మీద లేదు. కాబట్టి ఈ రేఖ నుంచి విభిన్నంగా ఉంటూ, దత్త రేఖల ఖండన బిందువు గుండాపోయే ఏదైనా రేఖ సమీకరణం
(x + y + 1) + λ (2x − y + 5) = 0 రూపంలో ఉంటుంది.
ఈ రేఖ (5, −2) బిందువు గుండా పోవాలంటే 4 + λ (17) = 0.
లేదా λ = – \(\frac{4}{17}\) కావాలి. అందువల్ల కావలసిన రేఖ సమీకరణం
17(x + y + 1) -4
(2x – y + 5) = 0
అంటే 9x + 21y – 3 = 0
లేదా 3x + 7y − 1 = 0