AP Inter 1st Year Maths 1A Important Questions Chapter 3 మాత్రికలు

Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 3 మాత్రికలు which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1A Important Questions Chapter 3 మాత్రికలు

సాధించిన సమస్యలు
(Solved Problems)

ప్రశ్న 1.
A = \(\left[\begin{array}{ccc}
2 & 3 & -1 \\
7 & 8 & 5
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & 0 & 1 \\
2 & -4 & -1
\end{array}\right]\) అయితే A + B కనుక్కోండి.
సాధన:
A + B = \(\left[\begin{array}{ccc}
2 & 3 & -1 \\
7 & 8 & 5
\end{array}\right]\) + \(\left[\begin{array}{ccc}
1 & 0 & 1 \\
2 & -4 & -1
\end{array}\right]\)
= \(\left[\begin{array}{lll}
3 & 3 & 0 \\
9 & 4 & 4
\end{array}\right]\)

ప్రశ్న 2.
\(\left[\begin{array}{ccc}
x-1 & 2 & y-5 \\
2 & 0 & 2 \\
1 & -1 & 1+a
\end{array}\right]=\left[\begin{array}{ccc}
1-x & 2 & -y \\
2 & 0 & 2 \\
1 & -1 & 1
\end{array}\right]\)
అయితే x, y, z, a విలువలు కనుక్కోండి.
సాధన:
మాత్రికల సమానత్వం ప్రకారం
x – 1 = 1 – x ⇒ 2x = 2 ⇒ x = 1
y – 5 = -y ⇒ 2y = 5 ⇒ y = \(\frac{5}{2}\)
z = 2 ⇒ z = 2
1 + a = 1 ⇒ a = 1 – 1 ⇒ a = 0

ప్రశ్న 3.
A = \(\left[\begin{array}{ccc}
1 & 2 & -\frac{1}{2} \\
0 & -1 & 2 \\
-\frac{1}{2} & 2 & 1
\end{array}\right]\) అయితే మాత్రికA జాడ కనుక్కోండి. [Mar. ’04]
సాధన:
1, −1, 1 లు ప్రధాన వికర్ణ మూలకాలు.
జాడ (A) = 1 + (-1) + 1 = 1

ప్రశ్న 4.
A = \(\left[\begin{array}{cc}
4 & -5 \\
-2 & 3
\end{array}\right]\) అయితే -5A కనుక్కోండి.
సాధన:
– 5A = -5\(\left[\begin{array}{cc}
4 & -5 \\
-2 & 3
\end{array}\right]\)
= \(\left[\begin{array}{cc}
-20 & 25 \\
10 & -15
\end{array}\right]\)

ప్రశ్న 5.
A = \(\left[\begin{array}{ccc}
\mathrm{i} & 0 & 1 \\
0 & -i & 2 \\
-1 & 1 & 5
\end{array}\right]\) అయితే Aకు సంకలన విలోమం కనుక్కోండి.
సాధన:
A కు సంకలన విలోమము -A = (-1)A
∴ A కు సంకలన విలోమము – (-1) \(\left[\begin{array}{ccc}
\mathrm{i} & 0 & 1 \\
0 & -\mathrm{i} & 2 \\
-1 & 1 & 5
\end{array}\right]\)
= \(\left[\begin{array}{ccc}
-\mathrm{i} & 0 & -1 \\
0 & \mathrm{i} & -2 \\
1 & -1 & -5
\end{array}\right]\)

ప్రశ్న 6.
A = \(\left[\begin{array}{ccc}
2 & 3 & 1 \\
6 & -1 & 5
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & -1 & 3
\end{array}\right]\) అయితే A + B – X = 0 అయ్యేటట్లుగా X మాత్రికను కనుక్కోండి. మాత్రిక X తరగతి ఎంత ?
సాధన:
A + B = X = 0
⇒ X = A + B
= \(\left[\begin{array}{ccc}
2 & 3 & 1 \\
6 & -1 & 5
\end{array}\right]\) + \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & -1 & 3
\end{array}\right]\)
∴ X = \(\left[\begin{array}{ccc}
3 & 5 & 0 \\
6 & -2 & 8
\end{array}\right]\)
∴ X మాత్రిక తరగతి 2 × 3.

ప్రశ్న 7.
A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
2 & 3 & 4 \\
4 & 5 & 6
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -2 & 0 \\
0 & 1 & -1 \\
-1 & 0 & 3
\end{array}\right]\) అయితే A – 3, 4B – 3A లను కనుక్కోండి.
సాధన:

ప్రశ్న 8.
A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ll}
3 & 8 \\
7 & 2
\end{array}\right]\), 2X + A = B అయితే మాత్రిక ‘X’ ను కనుక్కోండి. [(A.P) Mar. ’15, ’13]
సాధన:
2X + A = B ⇒ 2X = B – A
= \(\left[\begin{array}{ll}
3 & 8 \\
7 & 2
\end{array}\right]\) – \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\) = \(\left[\begin{array}{cc}
2 & 6 \\
4 & -2
\end{array}\right]\)
X = \(\frac{1}{2}\left[\begin{array}{cc}
2 & 6 \\
4 & -2
\end{array}\right]\)
∴ X = \(\left[\begin{array}{cc}
1 & 3 \\
2 & -1
\end{array}\right]\)

ప్రశ్న 9.
I, II అనే రెండు కర్మాగారాలు, జెల్, బాల్, ఇంక్ అనే మూడు రకాల పెన్నులను తయారు చేస్తాయి. సెప్టెంబరు, అక్టోబరు నెలల్లో ఈ రెండు కర్మాగారాల అమ్మకాల విలువ కింది మాత్రికలలో ఇచ్చాం.
సెప్టెంబర్ నెల అమ్మకాలు (రూపాయలలో)

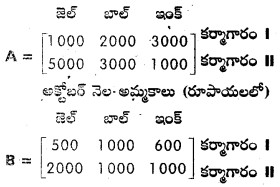
i) రెండు కర్మాగారాలకు సెప్టెంబర్, అక్టోబర్ లో మూడు రకాల పెన్నుల అమ్మకాల విలువ విడి విడిగా కనుక్కోండి.
ii) అక్టోబర్ లో తగ్గిన అమ్మకాల విలువ కనుక్కోండి.
సాధన:
i) రెండు కర్మాగారాల సెప్టెంబర్, అక్టోబర్ నెలల అమ్మకాల మొత్తం విలువ
జెల్ బాల్ ఇంక్

ii) అక్టోబర్ నెలలో తగ్గిన అమ్మకాలు

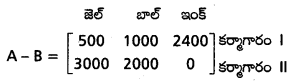
ప్రశ్న 10.
ఒక 3 × 2 మాత్రిక మూలకాలు a_ij = \(\frac{1}{2}\) |i – 3j| గా నిర్వచిస్తే, ఆ మాత్రికను నిర్మించండి. [T.S. Mar. ’15]
సాధన:
సాధారణంగా 3 × 2 మాత్రికను
A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{array}\right]\) గా సూచిస్తాం.
ఇప్పుడు a^ij = \(\frac{1}{2}\) |i – 3j| i = 1, 2, 3 ; j = 1, 2
a₁₁ = \(\frac{1}{2}\) |1 – (3 × 1)| = 1
a₁₂ = \(\frac{1}{2}\) |1 – (3 × 2)| = \(\frac{5}{2}\)
a₂₁ = \(\frac{1}{2}\) |2 – (3 × 1)| = \(\frac{1}{2}\)
a₂₂ = \(\frac{1}{2}\) |2 – (3 × 2)| = 2
a₃₁ = \(\frac{1}{2}\) |3 – (3 × 1)| = 0
a₃₂ = \(\frac{1}{2}\) |3 – (3 × 2)| = \(\frac{3}{2}\)
∴ A = \(\left[\begin{array}{cc}
1 & \frac{5}{2} \\
\frac{1}{2} & 2 \\
0 & \frac{3}{2}
\end{array}\right]\)

ప్రశ్న 11.
A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
2 & 3 & 4
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & -2 \\
-1 & 0 \\
2 & -1
\end{array}\right]\) అయితే AB, BA లను కనుక్కోండి.
సాధన:
మాత్రిక A లో నిలువు వరుసల సంఖ్య, మాత్రిక Bలో అడ్డు
వరుసల సంఖ్య = 3
కనుక AB నిర్వచితం
AB = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
2 & 3 & 4
\end{array}\right]\) \(\left[\begin{array}{cc}
1 & -2 \\
-1 & 0 \\
2 & -1
\end{array}\right]\)
= \(\left[\begin{array}{ll}
3 & -2 \\
5 & -5 \\
7 & -8
\end{array}\right]\)
B మాత్రికలో నిలువ వరుసల సంఖ్య ≠ A మాత్రికలోని అడ్డు వరుసల సంఖ్య
∴ BA నిర్వచితం కాదు.

ప్రశ్న 12.
A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
2 & 3 & -1 \\
-3 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 1 & 2 \\
1 & 2 & 0
\end{array}\right]\) లు వినిమయ న్యాయాన్ని పాటిస్తాయేమో పరిశీలించండి.
సాధన:
A, B లు రెండు 3వ తరగతి చతురస్ర మాత్రికలు.
కనుక AB, BA లు నిర్వచితం.

కనుక మాత్రిక గుణకారం వినిమయ ధర్మాన్ని పాటించదు.

ప్రశ్న 13.
A = \(\left[\begin{array}{cc}
\mathrm{i} & 0 \\
\mathrm{0} & -\mathrm{i}
\end{array}\right]\) అయితే A² = −I, (i = – 1) అని చూపండి.
సాధన:
A² = \(\left[\begin{array}{cc}
\mathrm{i} & 0 \\
\mathrm{0} & -\mathrm{i}
\end{array}\right]\) \(\left[\begin{array}{cc}
\mathrm{i} & 0 \\
\mathrm{0} & -\mathrm{i}
\end{array}\right]\)
= \(\left[\begin{array}{ll}
i^2 & 0 \\
0 & i^2
\end{array}\right]\)
= \(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\)
= (-1) \(\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]\) = -I

ప్రశ్న 14.
A = \(\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\) అయితే n యొక్క అన్ని ధనపూర్ణ విలువలకూ Aⁿ = \(\left[\begin{array}{cc}
\cos n \theta & -\sin n \theta \\
\sin n \theta & \cos n \theta
\end{array}\right]\) అని చూపండి.
సాధన:
దత్త ప్రవచనాన్ని S(n) అనుకోండి.

∴ S(k + 1) నిజం
గణితానుగమన నియమం ప్రకారం, n ∈ N కు S(n) నిజం.
∴ Aⁿ = \(\left[\begin{array}{cc}
\cos n \theta & -\sin n \theta \\
\sin n \theta & \cos n \theta
\end{array}\right]\) ∀ n ∈ N

ప్రశ్న 15.
A = \(\left[\begin{array}{lll}
1 & 2 & 2 \\
2 & 1 & 2 \\
2 & 2 & 1
\end{array}\right]\) అయితే A² – 4A – 5I = 0 అని చూపండి.
సాధన:

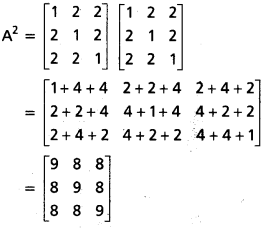
ప్రశ్న 16.
A = \(\left[\begin{array}{ccc}
-2 & 1 & 0 \\
3 & 4 & -5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 2 \\
4 & 3 \\
-1 & 5
\end{array}\right]\) అయితే A + B’ కనుక్కోండి.
3. A + B’
సాధన:
A + B’ = \(\left[\begin{array}{ccc}
-2 & 1 & 0 \\
3 & 4 & -5
\end{array}\right]\) + \(\left[\begin{array}{ccc}
1 & 4 & -1 \\
2 & 3 & 5
\end{array}\right]\)
= \(\left[\begin{array}{ccc}
-1 & 5 & -1 \\
5 & 7 & 0
\end{array}\right]\)

ప్రశ్న 17.
A = \(\left[\begin{array}{cc}
-1 & 2 \\
0 & 1
\end{array}\right]\) అయితే AA’ కనుక్కోండి. మాత్రికల గుణకారం దృష్ట్యా A, A’ లు వినిమయ ధర్మాన్ని పాటిస్తాయా ?
సాధన:

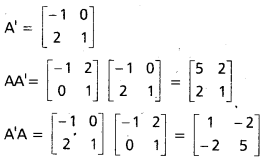
∵ AA’ ≠ A’A
A, A’ లు మాత్రికల గుణకారం దృష్ట్యా వినిమయ ధర్మాన్ని పాటించవు.

ప్రశ్న 18.
A = \(\left[\begin{array}{ccc}
0 & 4 & -2 \\
-4 & 0 & 8 \\
2 & -8 & x
\end{array}\right]\) ఒక వక్ర సౌష్ఠవ మాత్రిక అయితే ‘x’ విలువ ఎంత ?
సాధన:
A ఒక వక్ర సౌష్టవ మాత్రిక అయిన, దాని ప్రధాన వికర్ణ మూలకాలు అన్నీ సున్నాలే. కనుక x = 0.

ప్రశ్న 19.
A ఒక n వ తరగతి చతురస్ర మాత్రిక అయితే Aను ఒక సౌష్ఠవ మాత్రిక, ఒక వక్ర సౌష్ఠవ మాత్రికల మొత్తంగా ఏకైకంగా రాయవచ్చని నిరూపించండి.
సాధన:
A + A’ ఒక సౌష్టవ మాత్రిక
A – A’ ఒక వక్ర సౌష్ఠవ మాత్రిక
∴ A = \(\frac{1}{2}\) (A + A) + \(\frac{1}{2}\) (A – A’)
B ఒక సౌష్ఠవ మాత్రిక, C ఒక వక్ర సౌష్ఠవ మాత్రిక అయితే,
ఏకైకత నిరూపించడం కోసం A = B + C అనుకుందాం
అపుడు A’ = (B + C)’ = B’ + C’
= B + (C) = B – C
కనుక B = \(\frac{1}{2}\)(A + A’)
C = \(\frac{1}{2}\) (A – A’) అవుతాయి.

ప్రశ్న 20.
\(\left|\begin{array}{ccc}
1 & a & a^2 \\
1 & b & b^2 \\
1 & c & c^2
\end{array}\right|\) = (a – b) (b – c) (c – a) అని చూపండి. [‘Mar, ’05]
సాధన:

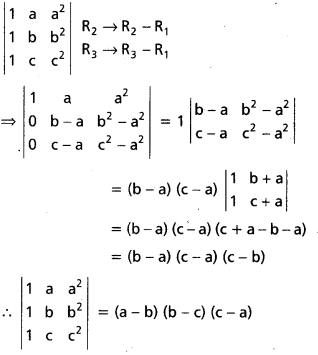
ప్రశ్న 21.
నిర్ధారకాన్ని విస్తరించకుండా
\(\left|\begin{array}{lll}
\mathrm{b}+\mathrm{c} & \mathrm{c}+\mathrm{a} & \mathrm{a}+\mathrm{b} \\
\mathrm{c}+\mathrm{a} & \mathrm{a}+\mathrm{b} & \mathrm{b}+\mathrm{c} \\
\mathrm{a}+\mathrm{b} & \mathrm{b}+\mathrm{c} & \mathrm{c}+\mathrm{a}
\end{array}\right|\) = 2\(\left|\begin{array}{lll}
\mathrm{a} & \mathrm{b} & \mathrm{c} \\
\mathrm{b} & \mathrm{c} & \mathrm{a} \\
\mathrm{c} & \dot{\mathrm{a}} & \mathrm{b}
\end{array}\right|\)
అని చూపండి. [(A.P) Mar. ’15]
సాధన:

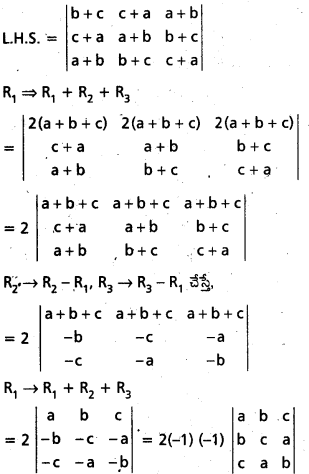
2\(\left|\begin{array}{lll}
\mathrm{a} & \mathrm{b} & \mathrm{c} \\
\mathrm{b} & \mathrm{c} & \mathrm{a} \\
\mathrm{c} & \dot{\mathrm{a}} & \mathrm{b}
\end{array}\right|\) = R.H.S.

ప్రశ్న 22.
\(\left|\begin{array}{ccc}
1 & a^2 & a^3 \\
1 & b^2 & b^3 \\
1 & c^2 & c^3
\end{array}\right|\) = (a – b) (b – c) (c – a) (ab + bc + ca) అని చూపండి.
సాధన:
L.H.S. = \(\left|\begin{array}{ccc}
1 & a^2 & a^3 \\
1 & b^2 & b^3 \\
1 & c^2 & c^3
\end{array}\right|\)
R₂ → R₂ – R₁, R₃ → R₃ – R₁
= \(\left|\begin{array}{ccc}
1 & a^2 & a^3 \\
0 & b^2-a^2 & b^2-a^3 \\
0 & c^2-a^2 & c^3-a^3
\end{array}\right|\)

= -(a – b)(b – c)(c – a) [(c² + ca + a²) – (b + c + a) (c + a)]
= -(a – b)(b – c)(c – a) [c² + ca + a² – b(c + a) – (c + a)²]
= -(a – b) (b – c) (c – a) [c² + ca + a² – bc – ab – c² – 2ca – a²]
= -(a – b)(b – c)(c – a)[-ab – bc – ca]
= (a – b) (b – c) (c – a) (ab + bc + ca)
∴ \(\left|\begin{array}{ccc}
1 & a^2 & a^3 \\
1 & b^2 & b^3 \\
1 & c^2 & c^3
\end{array}\right|\) = (a – b) (b – c) (c – a) (ab + bc + ca)

ప్రశ్న 23.
ω అనేది 1 యొక్క సంకీర్ణ ఘన మూలం అయితే \(\left|\begin{array}{ccc}
1 & \omega & \omega^2 \\
\omega & \omega^2 & 1 \\
\omega^2 & 1 & \omega
\end{array}\right|\) = 0 అని చూపండి. [Mar. ’14, ’11]
సాధన:

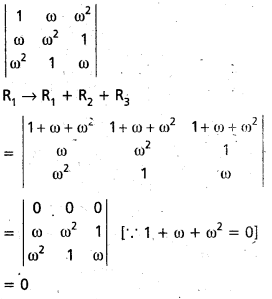
ప్రశ్న 24.
\(\left|\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\) = (a + b + c)³ అని చూపండి. [May ’11]
సాధన:

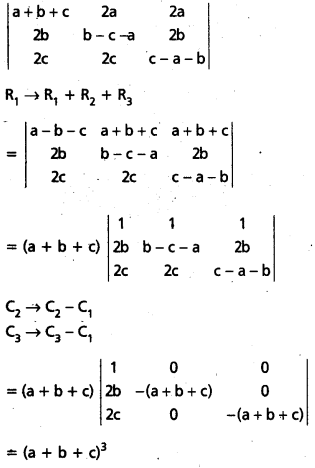
ప్రశ్న 25.
ఒక 3వ తరగతి వక్ర సౌష్ఠవ మాత్రిక నిర్ధారకం ఎప్పుడూ సున్నా అని చూపండి.
సాధన:

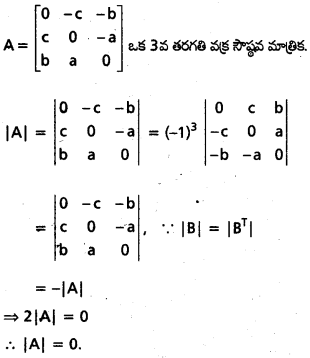
ప్రశ్న 26.
\(\left|\begin{array}{ccc}
x-2 & 2 x-3 & 3 x-4 \\
x-4 & 2 x-9 & 3 x-16 \\
x-8 & 2 x-27 & 3 x-64
\end{array}\right|\) = 0 అయితే x విలువ కనుక్కోండి. [(T.S) Mar. 15, ’06]
సాధన:

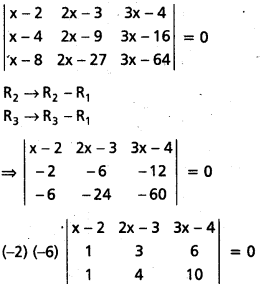
⇒ (x – 2) (30 – 24) – (2x – 3) (10 – 6) + (3x – 4) (4 – 3) = 0
⇒ 6x – 12 – 8x + 12 + 3x – 4 = 0
x – 4 = 0
∴ x = 4

ప్రశ్న 27.
A = \(\left[\begin{array}{cc}
1 & 2 \\
3 & -5
\end{array}\right]\) అయితే అను A, విలోమ మాత్రికను కనుక్కోండి.
సాధన:
|A| = \(\left[\begin{array}{cc}
1 & 2 \\
3 & -5
\end{array}\right]\) = -5 – 6 = -11 ≠ 0 .
A విలోమనీయం.

ప్రశ్న 28.
A = \(\left[\begin{array}{lll}
1 & 3 & 3 \\
1 & 4 & 3 \\
1 & 3 & 4
\end{array}\right]\) మాత్రికకు అనుబంధ మాత్రిక, విలోమ మాత్రికలను గణించండి.
సాధన:

ప్రశ్న 29.
A = \(\left[\begin{array}{lll}
1 & 2 & 1 \\
3 & 2 & 3 \\
1 & 1 & 2
\end{array}\right]\) కు విలోమ మాత్రికను కనుక్కోండి.
సాధన:
A = \(\left[\begin{array}{lll}
1 & 2 & 1 \\
3 & 2 & 3 \\
1 & 1 & 2
\end{array}\right]\)
det A = 1(4 – 3) – 2(6 – 3) + 1(3 – 2)
= 1 – 6 + 1 = -4
A లోని మూలకాల సహగుణావయాలు
A₁₁ =+ (4 – 3) = 1, A₁₂ = -(6 – 3) = -3,
A₁₃ = +(3 – 2) = 1, A₂₁ = -(4 – 1)= -3,
A₂₂ = +(2 – 1) = 1, A₂₃ = -(1 – 2) = 1,
A₃₁ = +(6 – 2) = 4, A₃₂ = -(3 – 3) = 0,
A₃₃ = + (2 – 6) = -4

ప్రశ్న 30.
A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 2 & 1
\end{array}\right]\) అయితే కోటి Aను ప్రాథమిక పరిక్రి యలను ఉపయోగించి కనుక్కోండి.
సాధన:

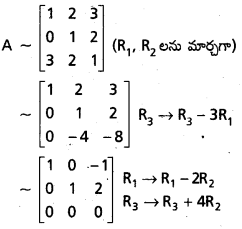
చివరి మాత్రిక అసాధారణం ; \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) అనే సాధారణ
ఉపమాత్రిక ఉంది.
కాబట్టి కోటి 2
∴ కోట (A) = 2.

ప్రశ్న 31.
A = \(\left[\begin{array}{cccc}
1 & 2 & 0 & -1 \\
3 & 4 & 1 & 2 \\
-2 & 3 & 2 & 5
\end{array}\right]\) అయితే కోటిని ప్రాథమిక పరిక్రియలను ఉపయోగించి కనుక్కోండి.
సాధన:

ప్రశ్న 32.
a) మాత్రిక కోటి ఉపయోగించి క్రింది సమీకరణాలు సంగతమేమో పరీక్షించండి.
2xy + 3z = 8,
-x + 2y + z = 4,
3x + y – 4z = 0 సంగతమైతే సాధన కనుక్కోండి.
సాధన:
సర్వ మాత్రిక

కోటి (A) = కోటి [AD] = 3
∴ కనుక దత్త వ్యవస్థ సంగతం.
ఏకైక సాధన ఉంటుంది.
(F) నుంచి తుల్య సమీకరణ వ్యవస్థను వ్రాస్తే
-x + 2y + z = 4
3y + 5z = 16
-38z = -76
∴ z = 2, y = 2, x = 2.

ప్రశ్న 33.
క్రింది సమీకరణ వ్యవస్థ సంగతమని చూపి, పూర్తిగా సాధించండి.
x + y + z = 3,
2x + 2y – z = 3,
x + y – z = 1.
సాధన:
A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
2 & 2 & -1 \\
1 & 1 & -1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) మరియు D = \(\left[\begin{array}{l}
3 \\
3 \\
1
\end{array}\right]\)
దత్త సమీకరణ వ్యవస్థకు మాత్రికా సమీకరణం
AX = D
సర్వ మాత్రిక

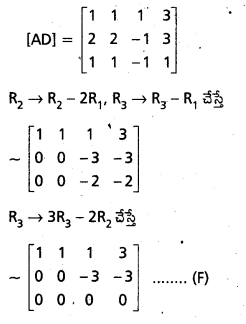
పై మాత్రికలో ప్రతి 3వ తరగతి చతురస్ర ఉపమాత్రికా అసాధారణం. కాబట్టి కోటి [A] ≠ 3, కోటి [AD] ≠ 3
\(\left[\begin{array}{cc}
1 & 1 \\
0 & -3
\end{array}\right]\) అనే సాధారణ మాత్రిక A కు, [AD] కు కూడా
ఉపమాత్రిక అవుతుంది.
కాబట్టి కోటి (A) = కోటి [AD] = 2
∴ దత్త సమీకరణ వ్యవస్థ సంగతం. అనంత సాధనాలు ఉంటాయి.
(F) నుంచి తుల్య సమీకరణ వ్యవస్థను వ్రాస్తే,
z + y + z = 3
-3z = -3 ⇒ z = 1
x + y = 2
∴ సాధన సమితి x = k, y = 2 – k, z = 1, k ∈ R.

ప్రశ్న 34.
క్రింది సమకాలిక సమీకరణాలను క్రేమర్ నియమం ఉపయోగించి సాధించండి.
3x + 4y + 5z = 18,
2x – y + 8z = 13,
5x – 2y + 7z = 20
సాధన:
A = \(\left[\begin{array}{ccc}
3 & 4 & 5 \\
2 & -1 & 8 \\
5 & -2 & 7
\end{array}\right]\) ; X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), D = \(\left[\begin{array}{l}
18 \\
13 \\
20
\end{array}\right]\)
i.e., AX = D

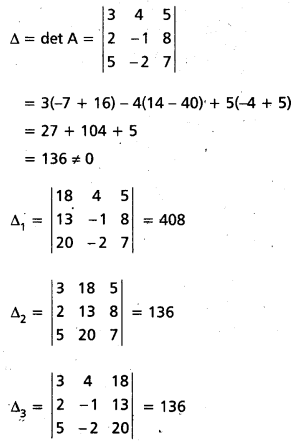
క్రేమర్ నియమం ఉపయోగించి
x = \(\frac{\Delta_1}{\Delta}=\frac{408}{136}\) = 3,
y = \(\frac{\Delta_2}{\Delta}=\frac{136}{136}\) = 1,
z = \(\frac{\Delta_3}{\Delta}=\frac{136}{136}\) = 1
∴ దత్త సమీకరణ సాధన x = 3, y = z = 1.

ప్రశ్న 35.
3x + 4y + 5z = 18; 2x – y + 8z = 13x అయితే 5x − 2y + 7z = 20 లను మాత్రికా విలోమ పద్ధతిని సాధించండి. [(A.P) Mar. ’15, ’13, ’08]
సాధన:
A = \(\left[\begin{array}{ccc}
3 & 4 & 5 \\
2 & -1 & 8 \\
5 & -2 & 7
\end{array}\right]\), X = \(\left[\begin{array}{c}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
18 \\
13 \\
20
\end{array}\right]\)
దత్త సమీకరణాల మాత్రికా రూపం AX = B
మాత్రికా విలోమ పద్ధతిని సాధన X = A^-1 B
det A = 3(-7 + 16) – 4(14 – 40) + 5(-4 + 5)
= 27 + 104 + 5
= 136
A లోని మూలకాల సహ గుణావయాలు
A₁₁ = +(-7 + 16) = 9,
A₁₂ = -(-14 – 40) = 26,
A₁₃ = +(-4 + 5) = 1,
A₂₁ = -(28 + 10) = -38,
A₂₂ = +(21 – 25) = -4,
A₂₃ = -(-6 – 20) = 26,
A₃₁ = +(32 + 5) = 37,
A₃₂ = -(24 – 10) = -14,
A₃₃ = (-3 – 8) =-11.

= \(\frac{1}{136}\left[\begin{array}{l}
408 \\
136 \\
136
\end{array}\right]=\left[\begin{array}{l}
3 \\
1 \\
1
\end{array}\right]\)
∴ సాధన x = 3, y = 1, z = 1.

ప్రశ్న 36.
క్రింది సమీకరణాలను గౌస్ జోర్డాన్ పద్ధతిని సాధించండి.
3x + 4y + 5z = 18,
2xy + 8z = 13,
5x-2y + 7z = 20.
సాధన:
సర్వ మాత్రిక = \(\left[\begin{array}{cccc}
3 & 4 & 5 & 18 \\
2 & -1 & 8 & 13 \\
5 & -2 & 7 & 20
\end{array}\right]\)
R₁ → R₁ – R₂ చేస్తే

R₃ → R₃ + (-680) చేస్తే
~\(\left[\begin{array}{cccc}
1 & 0 & 127 & 130 \\
0 & 1 & -26 & -25 \\
0 & 0 & 1 . & 1
\end{array}\right]\)
R₁ → R₁ – 127R₃, R₂ → R₂ + 26R₃ చేస్తే
~\(\left[\begin{array}{llll}
1 & 0 & 0 & 3 \\
0 & 1 & 0 & 1 \\
0 & 0 & 1 & 1
\end{array}\right]\)
కాబట్టి సాధన 5x = 3, y = 1, z = 1.

ప్రశ్న 37.
కింది సమీకరణ వ్యవస్థను గౌస్ జోర్డాన్ పద్ధతిని ఉపయోగించి సాధించండి.
x + y + z = 3,
2x + 2y – z = 3,
x + y – z = 1.
సాధన:
A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
2 & 2 & -1 \\
1 & 1 & -1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), D = \(\left[\begin{array}{l}
3 \\
3 \\
1
\end{array}\right]\) అనుకోండి.
దత్త సమీకరణాల మాత్రికా సమీకరణం AX = D.
సర్వ మాత్రిక

దత్త వ్యవస్థకు తుల్య వ్యవస్థ వ్రాస్తే
x + y + z = 3, -3z = -3
కాబట్ట z = 1, x + y = 2
∴ సాధన సమితి
x = k, y = 2 – k, z = 1, k ∈ R.

ప్రశ్న 38.
గౌస్ – జోర్డాన్ పద్ధతిని ఉపయోగించి కింది సమీకరణ వ్యవస్థకు సాధన లేదని చూపండి.
2x + 4y – z = 0,
x + 2y + 2z = 5,
3x + 6y – 7z = 2.
సాధన:


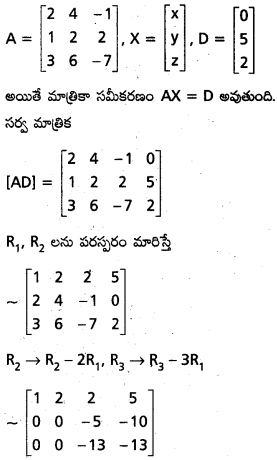
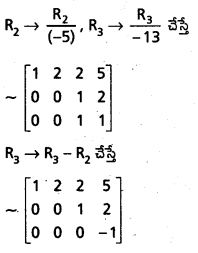
కాబట్టి దత్త సమీకరణ వ్యవస్థకు తుల్య వ్యవస్థను వ్రాస్తే
x + 2y + 2z = 5, z 5, z = 2
0(x) + 0(y) + 0(z) = −1
వీటిలో చివరి సమీకరణం x, y, Zఏ విలువలకూ ధ్రువపడదు. కాబట్టి దత్త సమీకరణ వ్యవస్థకు సాధన లేదు.

ప్రశ్న 39.
కింది సమీకరణాలకు తృణప్రాయం కాని సాధనలుంటే కనుక్కోండి.
2x + 5y + 6z = 0, x – 3y – 8z = 0, 3x + y – 4z = 0
సాధన:

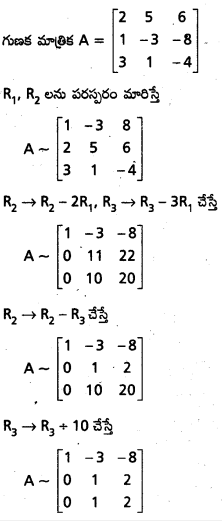
det A = 0 ∵ R₃ = R₂
ఉపమాత్రిక \(\left[\begin{array}{cc}
1 & -3 \\
0 & 1
\end{array}\right]\) సాధారణం కనుక కోటి (A) = 2
దత్త వ్యవస్థకు తృణప్రాయం కాని సాధన ఉంటుంది.
దత్త వ్యవస్థ x – 3y – 8z = 0
y + 2z = 0 అవుతుంది.
z = k అనుకుంటే
⇒ x = 2k, y = -2k, z = k, k ∈ R, k ≠ 0
అయితే తృణప్రాయం కాని సాధనలు వస్తాయి.

ప్రశ్న 40.
క్రింది సమఘాత ఏకఘాత సమీకరణ వ్యవస్థకు తృణ ప్రాయం’ కాని సాధన ఉందేమో కనుక్కోండి.
x – y + z = 0,
x + 2y – z = 0,
2x + y + 3z = 0
సాధన:
గుణక మాత్రిక \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
1 & 2 & -1 \\
2 & 1 & 3
\end{array}\right]\)
నిర్ధారకము 9 ≠ 0 కాబట్టి
దత్త వ్యవస్థకు x = y = z = 0 అనే తృణప్రాయ సాధన మాత్రమే ఉంటుంది.

ప్రశ్న 41.
సిద్ధాంతము : మాత్రికా గుణకారం సాహచర్య న్యాయాన్ని పాటిస్తుంది. (i.e.,) A, B, C లు మూడు మాత్రికలయితే (AB)C = A(BC) అవుతుంది. [June 01: Instant 93; 0ct. 83]
సాధన:
ఉపపత్తి : A = = (a_ij)_m×n
B = (b_ik)_n×p
C = (c_kl)_p×q అనుకోండి.


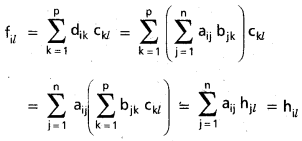
(AB) C = A (BC)

ప్రశ్న 42.
సిద్ధాంతము : మాత్రికల గుణకారం విభాగ న్యాయాలను పాటిస్తుంది. (i.e.,) A, B, C లు మూడు మాత్రికలైతే
i) A(B+ C) = AB + AC, [Oct. ’99, Instant ’98]
ii) (B + C)A = BA + CA
సాధన:

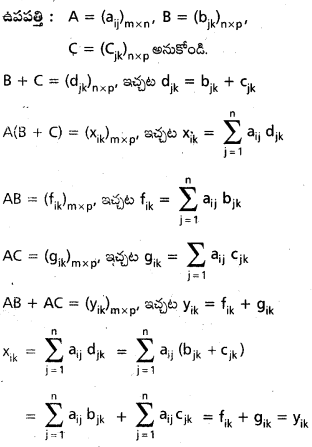
∴ A(B + C) = AB + AC
ఇదే విధంగా (B+ C)A = BA + CA.

ప్రశ్న 43.
సిద్ధాంతం: A ఏదేని మాత్రిక అయితే (A^T)^T = A అని చూపండి. [Nov. ’80]
సాధన:
A = (a_ij)_m×n అనుకోండి.
A^T = (a’_ji)_n×m, ఇచ్చట a’_ji = a_ij
(A^T)^T = (a”_ji)_m×n, ఇచ్చట a”_ij = a_ji
a”_ij = a’_ji = a_ij
∴ (A^T)^T = A.

ప్రశ్న 44.
సిద్ధాంతము: A, B లు రెండూ ఒకే తరగతి మాత్రికలు అయితే (A + B)^T = A^T + B^T. [July ’01]
సాధన:
ఉపపత్తి : A = (a_ij)_m×n, B = (b_ij)_m×n అనుకోండి.
A + B = (c_ij)_m×n, ఇచ్చట c_ij = a_ij + b_ij
(A + B)^T = (c’_ji)_n×m ఇచ్చట c’_ji = c_ij
A^T = (a’_ji)_n×m, ఇచ్చట a’_ji = a_ij
B^T = (b’_ji)_n×m, ఇచ్చట b’_kj = b_jk
A^T + B^T = (d_ji)_n×m, ఇచ్చట d_ji = a’_ji + b’_ji
c’_ji = c_ij = a_ij + b_ij = a’_ji + b’_ji = d_ji
∴ (A + B)^T = A^T + B^T.

ప్రశ్న 45.
సిద్ధాంతము: (AB)^T = B^TA^T. [July ’01; Mar. ’95, Nov. ’80]
సాధన:
ఉపపత్తి : A = (a_ij)_m×n, B = (b_jk)_n×p
AB = (c_ik)_m×p, ఇచ్చట c_ik = \(\sum_{j=1}^n a_{i j} b_{j k}\)
(AB)^T = (c’_ki)_p×m, ఇచ్చట c’_ki = c_ik
A^T = (a’_ji)_m×n, ఇచ్చట a’_ji = a_ij
B^T = (b’_kj)_p×n, ఇచ్చట b’_kj = b_jk
B^T. A^T = (d_ki)_p×m ఇచ్చట d_ki = \(\sum_{j=1}^n b_{k j}^{\prime} a_{j i}^{\prime}\)
c’_ki = c_ik = \(\sum_{j=1}^n a_{i j} b_{j k}=\sum_{j=1}^n b_{k j}^{\prime} a_{j i}^{\prime} d_{k i}\)
∴ (AB)^T = B^TA^T

ప్రశ్న 46.
సిద్ధాంతము : A, B లు రెండూ విలోమనీయ మాత్రికలు అయితే (AB)^-1 = B^-1A^-1 అనిచూపండి.
సాధన:
ఉపపత్తి : A విలోమనీయ మాత్రిక
⇒ A^-1 వ్యవస్థితము AA^-1 = A^-1A = I
B విలోమనీయ మాత్రిక ⇒ B^-1 వ్యవస్థితం
BB^-1 = B^-1B = I
ఇప్పుడు (AB) (B^-1A^-1) = A(BB^-1) A^-1
= AIA^-1 = AA^-1 = I
(B^-1A^-1) (AB) = B^-1 (A^-1A)B = B^-1IB
= B^-1B = I
∴ (AB) (B^-1A^-1) = (B^-1A^-1) (AB) = I
∴ AB విలోమనీయాం మరియు (AB)^-1 = B^-1A^-1.

ప్రశ్న 47.
సిద్ధాంతము : A విలోమనీయ మాత్రిక అయిన A^T కూడ విలోమనీయ మాత్రికలు అయిన (A^T)^-1 = (A ^-1)^T. [Nov. ’98]
సాధన:
ఉపపత్తి : A విలోమనీయ మాత్రిక ⇒ A^-1 వ్యవస్థితం మరియు
AA^-1 = A^-1A = I
(AA^-1)^T= (A^-1A)^T = I^T
⇒ (A^-1) A^T = A^T. (A^-1)^T = I
⇒ నిర్వచనం నుండి (A^T)^-1 = (A^-1)^T.

ప్రశ్న 48.
సిద్ధాంతము : A సాధారణ మాత్రిక మరియు విలోమనీయం A¹ = \(\frac{{Adj} \mathrm{A}}{{det} \mathrm{A}}\) అనిచూపండి.
[May ’13, ’07, ’06; Mar. ’07, ’02; Apr. ’99, ’94]
సాధన:

ప్రశ్న 49.
ఒక పుస్తకాల షాపులో 10 డజన్ల రసాయనశాస్త్రం పుస్తకాలు, 8 డజన్ల భౌతికశాస్త్రం పుస్తకాలు, 10 డజన్ల అర్థశాస్త్రం పుస్తకాలు ఉన్నాయి. ప్రతి పుస్తకం అమ్మకపు ధర వరసగా రూ. 80, రూ.60, రూ. 40 అయితే మాత్రికల బీజగణితం ఉపయోగించి, పుస్తకాల షాపులోని పుస్తకాల మొత్తం విలువను కనుక్కోండి.
సాధన:
పుస్తకాల సంఖ్య
రసాయనశాస్త్రం భౌతికశాస్త్రం అర్థశాస్త్రం
A = \(\left[\begin{array}{ccc}
10 \times 12 & 8 \times 12 & 10 \times 12 \\
=120 & =96 & =120
\end{array}\right]\)
అమ్మకపు విలువ (రూపాయలలో)

షాపులోని పుస్తకాల మొత్తం విలువ
AB = \(\left[\begin{array}{lcc}
120 & 96^* & 120
\end{array}\right]\left[\begin{array}{l}
80 \\
60 \\
40
\end{array}\right]\)
= [120 x 80 + 96 × 60 + 120 × 40]
= [9600 + 5760 + 4800]
= [20160] (రూపాయలలో).