AP Inter 1st Year Maths 1B Important Questions Chapter 8 అవధులు, అవిచ్ఛిన్నత

Students get through AP Inter 1st Year Maths 1B Important Questions Chapter 8 అవధులు, అవిచ్ఛిన్నత which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1B Important Questions Chapter 8 అవధులు, అవిచ్ఛిన్నత

సాధించిన సమస్యలు

ప్రశ్న 1.
\(\underset{\mathbf{x} \rightarrow -3}{\text { Lt }}\frac{1}{x+2}\) ను గణించండి.
సాధన:
f(x) = \(\frac{1}{x+2}\) అనుకొందాం.
h(x) = x + 2 ∀ x ∈ R గా వాస్త్రే

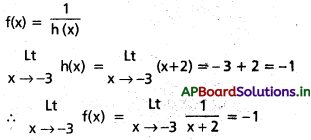
ప్రశ్న 2.
\(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\frac{x-2}{x^3-8}\) ను గణించండి.
సాధన:
f(x) = \(\frac{x-2}{x^3-8}\) x ≠ 2 గా వాస్త్రే
f(x) = \(\frac{x-2}{x^3-8}\) = \(\frac{1}{x^2+2 x+4}\)
h(x) = x² + 2x + 4
\(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\) = 2² + 2.2 + 4
= 4 + 4 + 4
= 12
\(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\frac{1}{\mathrm{~h}(\mathrm{x})}=\frac{1}{12}\)

ప్రశ్న 3.
\(\underset{\mathbf{x} \rightarrow 1}{\text { Lt }}\) (x + 2) (2x + 1) ను కనుక్కోండి.
సాధన:
\(\underset{\mathbf{x} \rightarrow 1}{\text { Lt }}\) (x + 2) (2x + 1)
= \(\underset{\mathbf{x} \rightarrow 1}{\text { Lt }}\) (x + 2) \(\underset{\mathbf{x} \rightarrow 1}{\text { Lt }}\) (2x + 1)
= (1 + 2) (1 + 2) = 3.3 = 9

ప్రశ్న 4.
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) x² . sin \(\frac{1}{x}\) ను గణించండి.
సాధన:
x ≠ 0, కు -1 ≤ sin \(\frac{1}{x}\) ≤ 1 అని తెలుసు
∴ – x² ≤ x² . sin \(\frac{1}{x}\) ≤ x²
కాని \(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) (- x²) = 0 = \(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) x²
సిద్ధాంతాన్ని అనుసరించి \(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) x² . sin \(\frac{1}{x}\) = 0 అని లభ్యం.

ప్రశ్న 5.
\(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\frac{x^2-5}{4 x+10}\) ను కనుక్కోండి.
సాధన:
f: R → R ను f(x) = x² – 5, అనీ
g: R→ R ను g(x) = 4x + 10

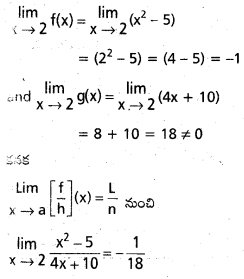
ప్రశ్న 6.
\(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\frac{x^3-6 x^2+9 x}{x^2-9}\) ను కనుక్కోండి.
సాధన:
F(x) = x³ – 6x² + 9x
= x(x – 3)² = (x – 3)
f(x) ఇక్కడ f(x) = x(x – 3)
G(x) = x² – 9= (x – 3) (x + 3)
= (x – 3) g(x) ఇక్కడ g(x) = x + 3
అందువల్ల \(\frac{F(x)}{G(x)}=\frac{(x-3) f(x)}{(x-3) g(x)}=\frac{f(x)}{g(x)}\)
g(3) = 6 ≠ 0.
ఇప్పుడు \(\underset{\mathbf{x} \rightarrow a}{\text { Lt }}\left[\frac{F}{G}\right](x)=\frac{f(a)}{f(x)}\) నుంచి
\(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\frac{x^3-6 x^2+9 x}{x^2-9}\) = \(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\frac{F(x)}{G(x)}\)
= \(\frac{f(3)}{g(3)}=\frac{3(3-3)}{3+3}=\frac{0}{6}\) = 0

ప్రశ్న 7.
\(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\frac{x^3-3 x^2}{x^2-5 x+6}\) ను కనుక్కోండి.
సాధన:
F(x) = x³ – 3x² = x³(x – 3) = (x – 3)
f(x), f(x) = x² అనీ
G(x)= x² – 5x + 6 = (x – 3) (x – 2)
= (x – 3) g(x), g(x) = x − 2
g(3) = 3 – 2 = 1 ≠ 0.
అందువల్ల, \(\underset{\mathbf{x} \rightarrow a}{\text { Lt }}\left[\frac{F}{G}\right](x)=\frac{f(a)}{g(a)}\) నుంచి
\(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\frac{x^3-3 x^2}{x^2-5 x+6}\) = \(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\frac{F(x)}{G(x)}=\frac{f(3)}{g(3)}=\frac{3^2}{3-2}\) = 9

ప్రశ్న 8.
\(\underset{\mathbf{x} \rightarrow 0+}{\text { Lt }}\frac{|\mathrm{x}|}{\mathrm{x}}\) = 1, \(\underset{\mathbf{x} \rightarrow 0-}{\text { Lt }}\frac{|\mathrm{x}|}{\mathrm{x}}\) = -1 (x ≠ 0) అని చూపండి.
సాధన:

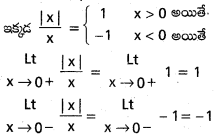
ప్రశ్న 9.
f : R → R, ద్వారా నిర్వచితమనుకోండి. అప్పుడు \(\stackrel{L t}{x \rightarrow 3}\) f(x) = 5 అని చూపండి.
సాధన:

ప్రశ్న 10.
\(\underset{\mathbf{x} \rightarrow -2}{\text { Lt }}\sqrt{x^2-4}\) = 0, \(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\sqrt{x^2-4}\) అని చూపండి.
సాధన:
(-2, 2) లో \(\sqrt{x^2-4}\) నిర్వచితం కాదు.
\(\underset{\mathbf{x} \rightarrow 2+}{\text { Lt }}\sqrt{x^2-4}\) = 0,
\(\underset{\mathbf{x} \rightarrow -2}{\text { Lt }}\sqrt{x^2-4}\) =0
కాబట్టి \(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\sqrt{x^2-4}\) = 0 = \(\underset{\mathbf{x} \rightarrow -2}{\text { Lt }}\sqrt{x^2-4}\) = 0

ప్రశ్న 11.
f(x) =
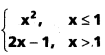, అయితే \(\underset{\mathbf{x} \rightarrow 1+}{\text { Lt }}\) f(x) \(\underset{\mathbf{x} \rightarrow 1-}{\text { Lt }}\) f(x) లను కనుక్కోండి.
\(\underset{\mathbf{x} \rightarrow 1}{\text { Lt }}\) f(x) వ్యవస్థితము ?
సాధన:

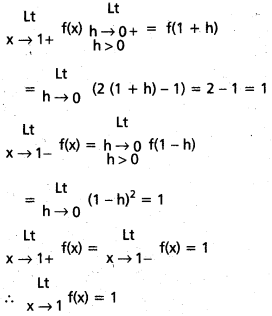
ప్రశ్న 12.
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\frac{\tan x}{x}\) = 1 అని చూపండి.
సాధన:

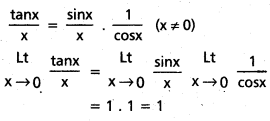
ప్రశ్న 13.
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\left\{\frac{\sqrt{1+x}-1}{x}\right\}\) ను కనుక్కోండి. [Mar. ’14]
సాధన:
0 |x| < 1 అయితే

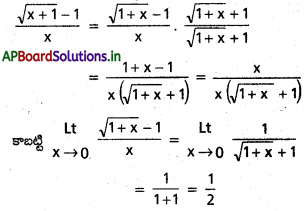
ప్రశ్న 14.
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\left[\frac{e^x-1}{\sqrt{1+x}-1}\right]\) ను గణించండి. [T.S Mar. 15]
సాధన:
0 < |x| < 1, అయితే

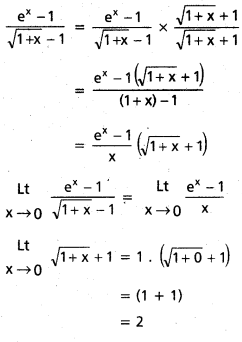
ప్రశ్న 15.
\(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\frac{x-3}{\sqrt{\left|x^2-9\right|}}\) = 0 అని చూపండి.
సాధన:

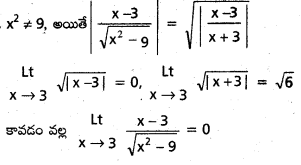
ప్రశ్న 16.
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\frac{a^x-1}{b^x-1}\) (a > 0, b > 0, b ≠ 1) ను గణించండి. [A.P.Mar. ’15, ’13]
సాధన:

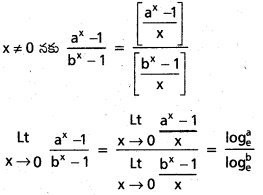
ప్రశ్న 17.
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\frac{\sin a x}{\sin b x}\), b ≠ 0, a ≠ b గణించండి.
సాధన:

ప్రశ్న 18.
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\frac{e^{3 x}-1}{x}\) ను గణించండి.
సాధన:

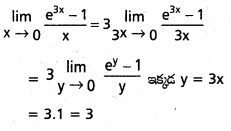
ప్రశ్న 19.
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\frac{e^x-\sin x-1}{x}\) ను గణించండి. [Mar. ’13]
సాధన:

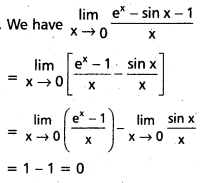
ప్రశ్న 20.
\(\underset{\mathbf{x} \rightarrow 1}{\text { Lt }}\frac{\log _e x}{x-1}\) కనుక్కోండి.
సాధన:
y = x – 1 అనుకోండి. ఇప్పుడు x → 1 అయినప్పుడు y → 0 అవుతుంది.

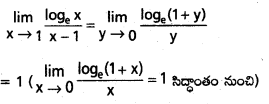
ప్రశ్న 21.
\(\underset{\mathbf{x} \rightarrow \infty}{\text { Lt }}\frac{1}{x^2}\) = 0 అని చూపండి.
సాధన:
E > 0, కు అనుగుణంగా α = \(\frac{1}{\sqrt{\varepsilon}}\) > 0 తీసుకోండి.
అప్పుడు x > α ⇒ x > \(\frac{1}{\sqrt{\varepsilon}}\) ⇒ x² > \(\frac{1}{\varepsilon} \Rightarrow \frac{1}{x^2}\) < ε
⇒ \(\left|\frac{1}{x^2}-0\right|\) < ε
\(\underset{\mathbf{x} \rightarrow \infty}{\text { Lt }}\frac{1}{x^2}\) = 0

ప్రశ్న 22.
\(\underset{\mathbf{x} \rightarrow \infty}{\text { Lt }}\) e^x = 0 అని చూపండి.
సాధన:
ఇచ్చిన k > 0 కు, అయినప్పుడు α = log k అనుకొందాం.
అప్పుడు x > α ⇒ e^x > e^α = k
\(\underset{\mathbf{x} \rightarrow \infty}{\text { Lt }}\) e^x = ∞

ప్రశ్న 23.
\(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\frac{x^2+2 x-1}{x^2-4 x+4}\) ను గణించండి.
సాధన:
f(x) = \(\frac{x^2-4 x+4}{x^2+2 x-1}=\frac{(x-2)^2}{x^2+2 x-1}\) వ్రాయండి.
2 విసర్జిత సామిష్యంలో f(x) > 0.
\(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\) f(x) = 0
\(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\frac{1}{f(x)}\) = ∞
\(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\frac{x^2+2 x-1}{x^2-4 x+4}\) = ∞

ప్రశ్న 24.
\(\underset{\mathbf{x} \rightarrow \infty}{\text { Lt }}\frac{3 x^5-1}{4 x^2+1}\) ను లెక్కించండి.
సాధన:

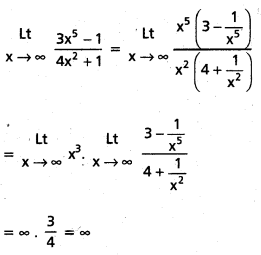
ప్రశ్న 25.

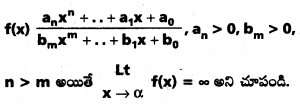
సాధన:

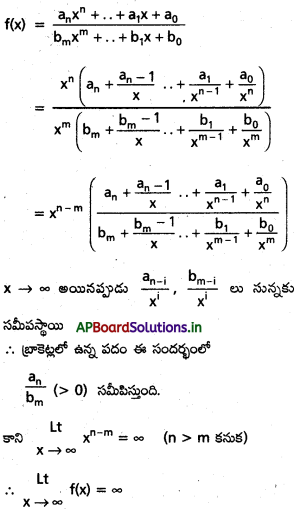
ప్రశ్న 26.
\(\underset{\mathbf{x} \rightarrow \infty}{\text { Lt }}\frac{x^2-\sin x}{x^2-2}\) ను గణించండి.
సాధన:
-1 ≤ sinx ≤1 ⇒ -1 ≤ -sinx ≤ 1 లభ్యం
అందువల్ల x² – 1 ≤ x² – sinx ≤ x² + 1
x → ∞, కనుక x² – 2 > 0

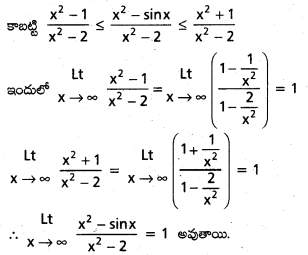
ప్రశ్న 27.
f(x) = [x] (x ∈ R) ప్రమేయం పూర్ణాంకాలు కాని అన్ని వాస్తవ సంఖ్యల వద్ద అవిచ్ఛిన్నం అని చూపండి.
సాధన:
సందర్భం i) : a ∈ z move f(a) = (a) = a

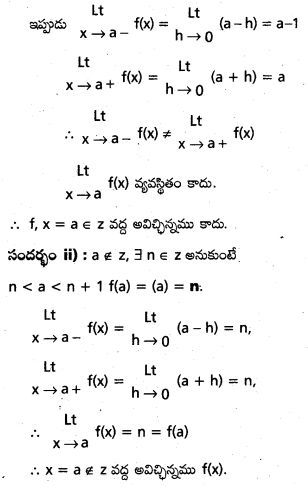
ప్రశ్న 28.
f : R → R, f(x + y) = f(x) + f(y), x, y ∈ R అయ్యేటట్లుంది. R లోని ఒక బిందువు వద్ద అవిచ్ఛిన్నమైతే అది R పై అవిచ్ఛిన్నం అని చూపండి.
సాధన:
x_o ∈ R వద్ద f అవిచ్ఛిన్నం అనుకోండి.

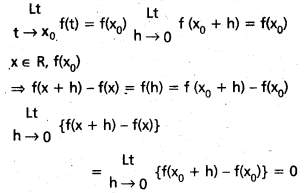
∴ f ప్రమేయము x = a వద్ద అవిచ్ఛిన్నం.
X ∈ R అవిచ్ఛిన్నం కనుక R మీద f అవిచ్ఛిన్నం.

ప్రశ్న 29.
1, 2 బిందువుల వద్ద క్రింది ప్రమేయం అవిచ్ఛిన్నతను పరిశీలించండి.

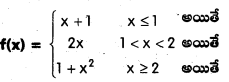
సాధన:


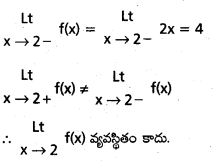
x = 2 వద్ద f అవిచ్ఛిన్నం కాదు.

ప్రశ్న 30.
f ప్రమేయాన్ని R మీద f(x) = cos x², X ∈ R అని నిర్వచిస్తే f అవిచ్ఛిన్న ప్రమేయమని చూపండి.
సాధన:
h : R → R ను h(x) = x²
g : R → Rను g(x) = cos x అని నిర్వచిద్దాం.
ప్రతీ x ∈ R కి,
(goh)(x) = g(h(x)) = g(x²)
= cos x² = f(x)
g, h లు వాటి ప్రదేశాల్లో అవిచ్ఛిన్నం కనక,
A, B, ⊆ R,
f : A → R, A మీద అవిచ్ఛిన్నం
g : B → R, B మీద అవిచ్ఛిన్నం
f(A) ⊆ B అయితే వాటి ప్రమేయం సంయుక్త ప్రమేయం
gof : A → R, A మీద అవిచ్ఛిన్నం, R మీద అవిచ్ఛిన్న ప్రమేయం.

ప్రశ్న 31.
ప్రమేయం f ను R మీద f(x) = -1 + 2x + |x||, x ∈ R అని నిర్వచిస్తే f అవిచ్ఛిన్నమని చూపండి.
సాధన:
g : R → R ను
g(x) = 1 + 2x + |x|, x ∈ R,
h : R → Rను h(x) = |x|, x ∈ R గా నిర్వచిద్దాం.
అప్పుడు
(hog) (x) = h(g(x)) = h(1 + 2x + |x|)
= |1 + 2x + |x|| = f(x).