AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Ex 10(g)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(g) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(g)

అభ్యాసం – 10 (జి)

I.

1. అవకలజాన్ని ఉపయోగించకుండా

i) f(x) = 3x + 7 ప్రమేయం R పై శుద్ధ ఆరోహణం సాధన.
సాధన:
x₁, x₂ ∈ R అయితే x₁ < x₂
3x₁ < 3x₂
ఇరువైపుల 7 కూడగా
3x₁ + 7 < 3x₂ + 7
⇒ f(x₁) < f(x₂)
∴ x₁ < x₂ ⇒ f(x₂) < f(x₂) ∀ x₁, x₂ ∈ R
ప్రమేయం R పై శుద్ధ ఆరోహణం.

ii) f(x) = \(\left(\frac{1}{2}\right)^x\) ప్రమేయం R పై శుద్ధ అవరోహణం
సాధన:
f(x) = \(\left(\frac{1}{2}\right)^x\)
Let x₁, x₂ ∈ R
అయితే
x₁ < x₂
⇒ \(\left(\frac{1}{2}\right)^{x_1}\) > \(\left(\frac{1}{2}\right)^{x_2}\)
⇒ f(x₁) > f(x₂) .
R పై f(x) శుద్ధ అవరోహణం.

iii) f(x) = e^3x ప్రమేయం R పై శుద్ధ ఆరోహణం.
సాధన:
f(x) = e^3x
x₁, x₂ ∈ R అయితే x₁ < x₂
W.k.t a > b
అయితే e^a > e^b
⇒ e^3x < e^3x₂
⇒ f(x₁) < f(x₂)
R పై f(x) శుద్ధ ఆరోహణం.

iv) f(x) = 5 – 7x ప్రమేయం R పై శుద్ధ అవరోహణం అని చూపండి.
సాధన:
f(x) = 5 – 7x
x₁ x₂ ∈R
అయిన x₁ < x₂
⇒ 7x₁ < 7x₂
-7x₁ > -7x₂
ఇరువైపులా 5 కూడగా
5 – 7x₁ > 5 – 7x₂
f(x₁) > f(x₂)
∴ x₁ < x₂ ⇒ f(x₁) > f(x₂) ∀x₁ x₂ ∈ R.
R పై f(x) శుద్ధ అవరోహణం.

ప్రశ్న 2.
f(x) = sin x, x E R ప్రమేయం R పై శుద్ధ ఆరోహణం లేదా శుద్ధ అవరోహణం కాదని చూపండి.
సాధన:
f(x) = sin x
Since 0 < x < π
Consider 0 < x f(0) < f(x)
sin 0 < sin x
0 < sin x —— (1)
Consider x < π
f(x) < f(π)
sin x < sin π 0 > sin x —— (2)
(1) (2) నుంచి f(x) శుద్ధ ఆరోహణం లేదా శుద్ధ అవరోహణం కాదు.

II.

1. కింద ప్రమేయాలు శుద్ధ ఆరోహణం, శుద్ధ అవరోహణం అయ్యే అంతరాలను కనుక్కోండి.

i) x² + 2x – 5
సాధన:
Let f(x) = x² + 2x – 5
f(x) = 2x + 2
f(x) ఆరోహణం అయితే f'(x) > 0
⇒ 2x + 2< 0 ⇒ x + 1 > 0
x > -1
x ∈ (-1, ∞) వద్ద f(x) ఆరోహణం
f(x) అవరోహణం అయితే f'(x) < 0
⇒ 2x + 2 < 0
⇒ x + 1 < 0
⇒ x < -1
x ∈ (-∞, −1) వద్ద f(x) అవరోహణం.

ii) 6 – 9x – x².
సాధన:
f(x) = 6 – 9x – x²
f'(x) = -9 -2x
f(x) ఆరోహణం అయితే f'(x) > 0
⇒ -9 – 2x > 0
⇒ 2x + 9 < 0
x < \(\frac{-9}{2}\)
x ∈ \(\left(-\infty, \frac{-9}{2}\right)\) అయితే f(x) ఆరోహణం
f(x) అవరోహణం అయితే f'(x) < 0
⇒ 2x + 9 > 0
⇒ x > \(\frac{-9}{2}\)
x ∈ \(\left(\frac{-9}{2}, \infty\right)\) అయితే f(x) అవరోహణం

iii) (x + 1)³ (x – 1)³.
సాధన:
Let f(x) = (x + 1)³ (x + 1)³
= (x² – 1)³
= x⁶ – 1 – 3x⁴ + 3x²
f'(x) = 6x⁵ – 12x³ + 6x
= 6(x⁵ – 2x³ + x)
= 6x(x⁴ – 2x² + 1)
= 6x(x² – 1)²
f'(x) ≤ 0
⇒ 6x(x² – 1) ≤ 0
f(x) అవరోహణ అయితే (-∞, -1) ∪ (1, 0)
f'(x) > 0
f(x) అవరోహణ అయితే (0, 1) ∪ (1, ∞)

iv) x³(x – 2)²
సాధన:
f'(x) = x³. 2(x – 2) + (x – 2)². 3x²
= x²(x – 2) (2x + 3(x – 2))
= x² (x – 2) (2x + 3x – 6)
= x² (x – 2) (5x – 6) ∀ x ∈ R, x² ≥ 0
ఆరోహణ అయితే f'(x) > 0.
x²(x – 2) (5x – 6) > 0
x ∈ \(\left(-\infty, \frac{6}{5}\right)\) ∪ (2, ∞)
అవరోహణ అయితే f'(x) < 0
x²(x – 2) (5x – 6) < 0
x ∈ \(\left(\frac{6}{5}, 2\right)\)

v) f(x) = x e^x
సాధన:
f(x) = x . e^x + e^x. 1 = e^x (x + 1)
e^x, x వాస్తవ
f(x) > 0 ⇒ x + 1 > 0 ⇒ x > -1
f(x) ఆరోహణం అయితే x > -1
f'(x) < 0 ⇒ x + 1 < 0 ⇒ x < – 1
f(x) అవరోహణము అయితే x < – 1

vi) f(x) = \(\sqrt{25-4 x^2}\)
సాధన:
f(x) వాస్తవము కావలెనంటే 25 – 4x² ≥ 0
-(4x² – 25) ≥ 0
-(2x + 5) (2x – 5) ≥ 0
∴ x విలువ \(-\frac{5}{2}\), \(\frac{5}{2}\) మధ్య ఉంటుంది.

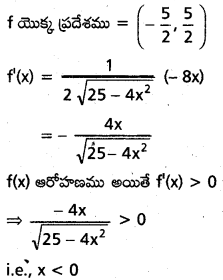
f(x) ప్రమేయము (\(-\frac{5}{2}\), 0) లో అవరోహణము
f(x) అవరోహణము అయితే f'(x) < 0
⇒ \(-\frac{4 x}{\sqrt{25-4 x^2}}\) < 0
∴ x > 0
f(x) ప్రమేయము (0, \(\frac{5}{2}\)) లో అవరోహణం.

vii) f(x) = ln (lnx); x > 1
సాధన:
f(x) = \(\frac{1}{\ln x} \cdot \frac{1}{x}\)
f(x) లో ఆరోహణమయితే f'(x) > 0
\(\frac{1}{x \cdot \ln } x\) > 0
⇒x. ln x > 0
In x వాస్తవం అయితే x > 0 కావలెను
∴ ln x < 0 = ln 1 i.e., x > 1
f(x) ప్రమేయము x > 1 ie., (1, ∞) అయిన ఆరోహణం
f(x) ప్రమేయము f'(x) < 0 అయితే అవరోహణం
⇒ In x > 0 ln
i.e., x < 1
f(x) ప్రమేయము (0, 1) లో అయితే అవరోహణం

viii) f(x) = x³ – 3x² – 6x + 12
సాధన:
f'(x) = 3x² + 6x – 6
= 3(x² + 2x – 2)
= 3[(x + 1)² – 3]
= 3( x + 1 + \(\sqrt{3}\)) ( x + 1 – \(\sqrt{3}\))
f'(x) = 3(x+ (\(\sqrt{3}\) + 1))(x + (1 − \(\sqrt{3}\)))
f'(x) ≤ 0 ⇒ 1 + \(\sqrt{3}\) < x < \(\sqrt{3}\) + 1
f(x), (1 + \(\sqrt{3}\), \(\sqrt{3}\) – 1) లో
f'(x) > 0 ⇒ x అవరోహణము
1 – \(\sqrt{3}\), \(\sqrt{3}\) – 1 ల మధ్య ఉండును.
i.e., x < 1 – \(\sqrt{3}\) మరియు x > \(\sqrt{3}\) – 1
f(x), x < 1 – \(\sqrt{3}\), x > \(\sqrt{3}\) – 1 లో ఆరోహణము

ప్రశ్న 2.
(0, π/2) అంతరంపై f(x) = cos²x శుద్ధ అవరోహణం అని చూపండి.
సాధన:
f(x) = cos²x
⇒ f'(x) = 2 cos x(-sin x)
= -2 sin x cos X
= -sin 2x
∴ 0 < x < \(\frac{\pi}{2}\)
⇒ 0 < 2x < π
‘sin x’ is +ve మధ్య 0 + π
∴ f'(x) = -ve.
∴ f'(x) < 0
∴ f(x) విలువ తగ్గుతుంది.

ప్రశ్న 3.
[1, ∞) అంతరం పై x + \(\frac{1}{x}\) ఆరోహణం అని చూపండి.
సాధన:
f(x) = x + \(\frac{1}{x}\)
f'(x) = 1 – \(\frac{1}{x^2}\) = \(\frac{x^2-1}{x^2}\)
Since x ∈ [1, ∞) = \(\frac{x^2-1}{x^2}\) > 0
∴ f(x) > 0
∴ f(x) ఆరోహణం.

ప్రశ్న 4.
ప్రతి x > 0 కి \(\frac{x}{1+x}\) < ln (1 + x) < x ∀ అని చూపండి.
సాధన:

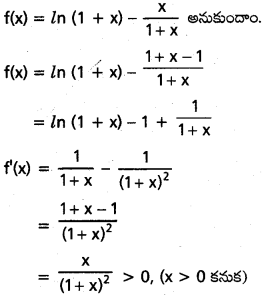
f(x) ప్రమేయము > 0 అయితే ఆరోహణము
∴ f(x) > f(0)

g(x) ప్రమేయము x > 0 లో ఆరోహణము
i.e., g(x) > g(0)
g(0) = 0 – ln = 0 – 0 = 0
∴ x – ln (1 + x) > 0
x > ln (1 + x) —– (2)
(1), (2) ల నుండి
x > 0 అయితే \(\frac{x}{1+x}\)(1 + x) < x

III.

ప్రశ్న 1.
ప్రతి x > 0 కి \(\frac{x}{1+x}\) < ln(1 + x) < x ∀ అని చూపండి.
సాధన:

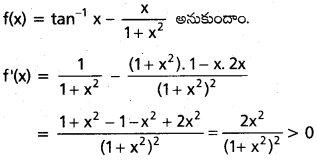
f(x) ప్రమేయము x > 0 లో ఆరోహణము
f(x) > f(0)
f(0) = tan^-1 0 – 0 = 0 కనుక
i.e., f(x) > 0
⇒ tan^-1x – \(\frac{x}{1+x^2}\) > 0
⇒ tan^-1x > \(\frac{x}{1+x^2}\) —- (1)
g(x) = 1 – tan^-1x అనుకుందాం
g'(x) = 1 – \(\frac{1}{1+x^2}\) = \(\frac{1+x^2-1}{1+x^2}\) = \(\frac{x^2}{1+x^2}\) > 0
g(x) ప్రమేయము x > 0 కు ఆరోహణము
i.e., g(x) > g(0)
g(0) = 0 – tan^-1 = 0 – 0 = 0
∴ x – tan^-1 x > 0
⇒ x > tan^-1 x —— (2)
(1), (2) ల నుండి
x > 0 అయితే \(\frac{x}{1+x^2}\) < tan^-1 x < x

ప్రశ్న 2.
ప్రతి x ∈\(\left(0, \frac{\pi}{2}\right)\) కి tan x > x అని చూపండి.
సాధన:
f(x) = tan x – x అనుకుందాం
f'(x) = sec² x – 1 > 0, ∀x ∈ \(\left(0, \frac{\pi}{2}\right)\),
∴ f(x) ప్రమేయము x ∈ \(\left(0, \frac{\pi}{2}\right)\) కు ఆరోహణము
i.e., f(x) > f(0)
f(0) = tan 0 – 0 = 0 – 0 = 0
∴ tan x – x > 0
⇒ ప్రతి x ∈ \(\left(0, \frac{\pi}{2}\right)\) కు tan x > x

ప్రశ్న 3.
x ∈ \(\left(0, \frac{\pi}{2}\right)\) అయితే, \(\frac{2 x}{\pi}\) < sin x < x అని చూడండి
సాధన:
f(x) = x – sinx అనుకుందాం.
f'(x) = 1 – cos x > 0 ∀ x ∈ \(\left(0, \frac{\pi}{2}\right)\)
⇒ f(x) ప్రమేయము ప్రతి x ∈ \(\left(0, \frac{\pi}{2}\right)\) కు ఆరోహణము.
⇒ f(x) > f(0)
f(0) = 0 – sin 0 = 0 – 0 = 0
∴ x – sin x > 0
⇒ x > sin x
g(x) = sin x – \(\frac{2 x}{\pi}\) అనుకుందాం.
g'(x) = cos x – \(\frac{2}{\pi}\) > 0 ప్రతి x ∈ \(\left(0, \frac{\pi}{2}\right)\) కు ప్రమేయము.
g(x) ప్రమేయము \(\left(0, \frac{\pi}{2}\right)\) లో ఆరోహణ ప్రమేయము.
g(x) > g(0)
g(0) = sin 0 – 0 = 0 – 0 = 0
∴sin x – \(\frac{2 x}{\pi}\) > 0
⇒ 1 – sin x > \(\frac{2 x}{\pi}\) —- (2)
(1), (2) ల నుండి
\(\frac{2 x}{\pi}\) < sin x < x ∀ x ∈ \(\left(0, \frac{\pi}{2}\right)\)

ప్రశ్న 4.
x ∈(0, 1) అయితే 2x < ln \(\left[\frac{(1+x)}{1-x}\right]\) < 2x \(\left[1+\frac{x^2}{2\left(1-x^2\right)}\right]\) అని చూపండి.
సాధన:

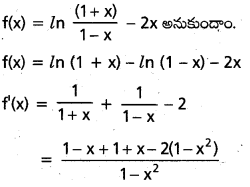
= \(\frac{2-2+2 x^2}{1-x^2}\)
= \(\frac{2 x^2}{1-x^2}\) > 0 ∀ x ∈ (0, 1)
f(x) ప్రమేయము (0, 1) లో ఆరోహణము
i.e., x > 0 ⇒ f(x) > f(0)
f(0) = ln 1 – 0 = 0 – 0 = 0

g(x) ప్రమేయము x > 0 కు ఆరోహణము
g(x) > g(0)
g(0) = 0 ln 1 = 0 – 0 = 0

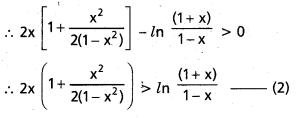
(1), (2) ల నుండి
2x < ln \(\frac{(1+x)}{1-x}\) < 2x \(\left(1+\frac{\mathrm{x}^2}{2\left(1-\mathrm{x}^2\right)}\right)\) x ∈ (0, 1)

ప్రశ్న 5.
y = \(\frac{x^3}{6}\) – \(\frac{3 x}{2}\) + \(\frac{11 x}{2}\) + 12 ప్రమేయానికి ఏ బిందువు వద్ద స్పర్శరేఖ వాలులు పెరుగుతాయి ?
సాధన:
వక్రం సమీకరణము У = \(\frac{x^3}{6}\) – \(\frac{3}{2} x^2\) + \(\frac{11 x}{2}\) + 12

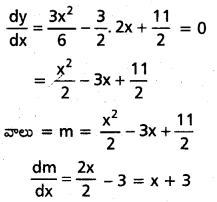
వాలు ఆరోహణము
⇒ m > 0
x – 3 > 0
x > -3
వాలు (3, ∝) లో ఆరోహణము

ప్రశ్న 6.
(0, ∝) అంతరంలో ln\(\frac{(1+x)}{x}\), \(\frac{x}{(1+x) \ln (1+x)}\) ప్రమేయాలు అవరోహణం అని చూపండి.
సాధన:
i)

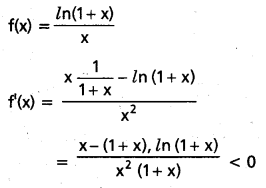
∴ f(x) ప్రమేయము x ∈ (0, ∝) లో అవరోహణ ప్రమేయము

ii)
f(x) = \(\frac{x}{(1+x) \ln (1+x)}\) అనుకుందాం


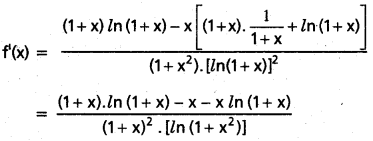
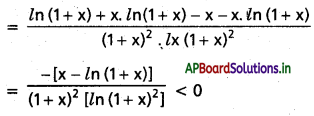
∴ f(x) ప్రమేయము x ∈ (0, ∝) లో అవరోహణ ప్రమేయము

ప్రశ్న 7.
f(x) = x³ – 3x² + 4 ∀ x ∈ R అంతరంలో శుద్ధ అవరోహణం అవుతుందో కనుక్కోండి
సాధన:
f(x) = x³ – 3x² + 4
f'(x) = 3x² – 6x
f(x) is increasing if f'(x) > 0
3x² – 6x > 0
3x(x – 2) > 0
(x – 0) (x – 2) > 0
f(x) is increasing if x ∈ (-∞, 0) ∪ (0, ∞)
f(x) is decreasing if f'(x) < 0
(x – 0) (x – 2) < 0
x ∈ (0, 2)

ప్రశ్న 8.
f(x) = sin⁴x + cos⁴x ∀ x ∈ \(\left[0, \frac{\pi}{2}\right]\), అంతరాలలో అవరోహణమో, ఆరోహణమో చూపండి.
సాధన:
f(x) = sin⁴x + cos⁴x
f(x) = (sin²x)² + (cos²x)²
= (sin²x + cos²x)² – 2sin²x cos²x
= 1 – \(\frac{1}{2}\) sin² 2x
f'(x) = \(\frac{-1}{2}\) sin 2x. cos 2x(2)
= -2 sin 2x . cos 2x
= -sin 4x
Let 0 < x < \(\frac{\pi}{4}\)
∴ f(x) విలువ తగ్గుతుంది f'(x) < 0
−sinx < 0 sinx > 0
∴ x ∈ \(\left(0, \frac{\pi}{4}\right)\)
f(x) విలువ పెరుగుతుంది f'(x) > 0
– sinx > 0
sinx < 0
x ∈ \(\left(\frac{\pi}{4}, \frac{\pi}{2}\right)\)