AP Inter 1st Year Maths 1B Solutions Chapter 2 అక్ష పరివర్తనం Ex 2(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 2 అక్ష పరివర్తనం Exercise 2(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 2 అక్ష పరివర్తనం Exercise 2(a)

అభ్యాసం – 2 (ఎ)

I.

ప్రశ్న 1.
అక్షాల సమాంతరపరివర్తన ద్వారా మూలబిందువును (4, −5) కు మారిస్తే కొత్త అక్షాల దృష్ట్యా క్రింది బిందువుల నిరూపకాలు కనుక్కోండి.
i) (0, 3),
ii) (−2, 4)
iii) (4, -5)
సాధన:
i) కొత్త మూలబిందువు = (4, -5); h = 4, k = -5
పాత నిరూపకాలు (0, 3)
నిరూపకాక్షాలకు 8 కోణం భ్రమణం చేయవలెను.
tan 2θ = \(\frac{2 h}{a-b}\) ; x = 0, y = 3
x’ = x – h= 0 – 4 = -4
y’ = y – k = 3 + 5 = 8
నూతన నిరూపకాలు (-4, 8)

ii) పాత నిరూపకాలు (-2, 4)
x = -2, y = 4
x’ = x – h = -2 -4 = -6
y’ = y – k = 4 + 5 = 9
నూతన నిరూపకాలు (-6, 9)

iii) పాత నిరూపకాలు (4, -5)
x = 4, y = -5
x’ =x-h=4 – 4 = 0
y’ = y – k = -5 + 5 = 0
నూతన నిరూపకాలు (0, 0)

ప్రశ్న 2.
అక్షాల సమాంతర పరివర్తనద్వారా మూలబిందువు (2, 3) కు మారింది. P బిందువు నిరూపకాలు క్రింది విధంగా మారితే, మూల వ్యవస్థలో P నిరూపకాలు కనుక్కోండి.
i) (4, 5)
ii) (4, -3),
iii) (0, 0)
సాధన:
i) నూతన నిరూపకాలు (4, 5)
x’ = 4, y’ = 5
x = x + h = 4 + 2= 6
y = y’ + k = 5 + 3 = 8
పాత నిరూపకాలు (6, 8)

ii) నూతన నిరూపకాలు (-4, 3)
x’ = -4, y’ = 3
x = x’ + h = 4 + 2 = -2
y = y’ + k = 3 + 3 = 6
పాత నిరూపకాలు (−2, 6)

iii) నూతన నిరూపకాలు (0, 0)
x’ = 0, y’ = 0
x = x’ + h = 0 + 2 = 2
y = y’ + k = 0 + 3 = 3
పాత నిరూపకాలు (2, 3)

ప్రశ్న 3.
అక్షాల సమాంతర పరివర్తన ద్వారా బిందువు (3, 0)ను (2, −3) కు మార్చడానికి మూలబిందువును ఏబిందువుకు మార్చాలో తెలపండి.
సాధన:
(x, y) = (3, 0)
(x’, y’) = (2, −3)
మూల బిందువు (h, k) కు మార్చవలెను
h = x – x’ = 3 – 2 = 1
k = y – y = 0 + 3 = 3
∴ (h, k) = (1, 3)

ప్రశ్న 4.
అక్షాల సమాంతర పరివర్తన ద్వారా మూలబిందువును (−1, 2) కు మారిస్తే క్రింది సమీకరణల రూపాంతరాలను కనుక్కోండి.
i) x² + y² + 2x – 4y + 1 = 0
ii) 2x² + y² – 4x + 4y = 0
సాధన:
i) దత్త సమీకరణము
x² + y² + 2x – 4y + 1 = 0
మూల బిందువు (−1, 2) కు మార్చవలెను
h = -1, k = 2
పరివర్తన సమీకరణాలు
x = x’ + h, y = y + k
i.e., x = x’ – 1, y = y + 2
రూపాంతర సమీకరణము (x’ – 1)² + (y + 2)²
+ 2(x’ – 1) – 4(y’ + 2) + 1 = 0
(x’)² + 1 − 2x’ + (y’)² + 4 + 4y’ + 2x’ – 2 – 4y’ – 8 + 1 = 0
(x’)² + (y’)² − 4 = 0

ii) పాత సమీకరణము 2x² + y² – 4x + 4y = 0
నూతన సమీకరణము 2 (x’ – 1)² + (y + 2)² -4(x’ – 1) + 4(y + 2) = 0
2[(x’)² + 1 – 2x’] + (y’)² + 4 + 4y’ – 4x’ + 4 + 4y’ + 8 = 0
2(x’)² + 2 – 4x’ + (y’) ² + 4 + 4y’ – 4x + 4 + 4y’ + 8 = 0
2(x’)² + (y’)² = 8x’ + 8y + 18 = 0

ప్రశ్న 5.
అక్షాల సమాంతర పరివర్తన ద్వారా మూలబిందువును ఏ బిందువుకు మార్చిందీ, తద్వారా రూపాంతరం చెందిన సమీకరణము క్రింద ఇవ్వడమైంది. మూలసమీకరణాన్ని కనుక్కోండి.
i) (3, – 4); x² + y² = 4
ii) (-1, 2); x² + 2 y² + 16 = 0.
సాధన:
i) మూల బిందువును = (3, -4) = (h, k) కు మార్చవలెను
x’ = x -h,
= x – 3
y’ = y-k
= y + 4
మూల సమీకరణము (x’)² + (y’)² = 4
(x – 3)² + (y + 4) ² = 4
x² – 6x + 9 + y² + 8y + 16
∴ x² + y² – 6x + 8y + 21 = 0

ii) మూల బిందువు = (h, k) = (-1, 2) కు మార్చవలెను.
x’ = x – h,
= x + 1
y’ = y – k
= y – 2
= 4
x’² + 2y’² + 16 = 0 యొక్క మూల సమీకరణము
(x + 1)² + 2(y – 2)² + 16 = 0
x² + 2x + 1 + 2y² – 8y + 8 + 16 = 0
x² + 2y² + 2x – 8y + 25 = 0

ప్రశ్న 6.
4x² + 9y² – 8x + 36y + 4 = 0 సమీకరణంలో మొదటి తరగతి పదాలు లోపింపచేయడానికి మూల బిందువును ఏ బిందువుకు మార్చాలో కనుక్కోండి.
సాధన:
దత్త సమీకరణము
4x² + 9y² – 8x + 36y + 4 = 0
a = 4
b = 9
g = – 4
f = 18
– \(\frac{g}{a}=\frac{4}{4}\) = 1, –\(\frac{f}{b}=-\frac{18}{9}\) = -2
మూల బిందువు (1, 2) కు పరివర్తన చేయవలెను.

ప్రశ్న 7.
30° కోణంతో అక్షాలను భ్రమణం చేసినప్పుడు, క్రింది బిందువుల కొత్త నిరూపకాలను కనుక్కోండి.
i) (0, 5)
ii) (−2, 4)
iii) (0, 0)
సాధన:
i) θ = 30° అని యివ్వబడింది. పాత నిరూపకాలు (0, 5)
x = 0, y = 5
x’ = x. cos θ + y. sin θ
= 0. cos 30° + 5. sin 30° = \(\frac{5}{2}\)
y’ = -x sin θ + y cos θ
=-0. sin 30° + 5 cos 30° = \(\frac{5 \sqrt{3}}{2}\)
పరివర్తన నిరూపకాలు \(\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)\)

ii) పాత నిరూపకాలు (-2, 4)
x = -2, y = 4
x’ = x cos θ + y sin θ
= (-2). cos 30° + 4. sin 30°
= -2 . \(\frac{\sqrt{3}}{2}\) + 4 . \(\frac{1}{2}\) = –\(\sqrt{3}\) + 2
y’ = – x sin θ + y cos θ
= (− 2). sin 30° + 4. cos 30°
= -2 . \(\frac{1}{2}\) + 4 . \(\frac{\sqrt{3}}{2}\)
= 1 + 2\(\sqrt{3}\)
∴ పరివర్తన నిరూపకాలు (-\(\sqrt{3}\) + 2, 1+ 2\(\sqrt{3}\))

iii) (x, y) = (0, 0) మరియు θ = 30° అని యివ్వబడింది.
x = (0, y) ⇒ x = x. cos 30° – y sin 30°
= 0 . \(\frac{\sqrt{3}}{2}\) – 0 . \(\frac{1}{2}\) = 0
y = x. sin 30° + y.cos 30°
= 0 . \(\frac{1}{2}\) + 0 . \(\frac{\sqrt{3}}{2}\) = 0
పరివర్తన నిరూపకాలు (0, 0)

ప్రశ్న 8.
60° కోణంతో అక్షాలను భ్రమణం చేసినప్పుడు, మూల బిందువుల కొత్త నిరూపకాలను ఇవ్వడమైంది.
i) (3, 4),
ii) (-7, 2)
iii) (2, 0) మూల వ్యవస్థలో ఈ బిందువుల నిరూపకాలు కనుక్కోండి.
సాధన:
i) θ = 60° అని యివ్వబడింది.
నూతన నిరూపకాలు (3, 4)
x’ = 3, y’ = 4
x = x’ cos θ – y’ sin θ
= 3. cos 60° – 4. sin 60°
= 3 . \(\frac{1}{2}\) – \(\frac{4 \cdot \sqrt{3}}{2}\) = \(\frac{3-4 \sqrt{3}}{2}\)

y = x’ sin θ + y’ cos θ
= 3 sin 60° + 4. cos 60°
= \(\text { 3. } \frac{\sqrt{3}}{2}+4 \cdot \frac{1}{2}=\frac{4+3 \sqrt{3}}{2}\)
P తొలి నిరూపకాలు \(\left(\frac{3-4 \sqrt{3}}{2}, \frac{4+3 \sqrt{3}}{2}\right)\)

ii) నూతన నిరూపకాలు (−7, 2)
x’ = 7, y’ = 2
x = x’ cos θ – y’ sin θ
= (-7) cos 60° – 2. sin 60°
= -7 . \(\frac{1}{2}-2 \cdot \frac{\sqrt{3}}{2}=\frac{-7-2 \sqrt{3}}{2}\)
y = x’ sin θ + y’. cos θ
= -7. sin 60° + 2. cos 60°
= -7 . \(\frac{\sqrt{3}}{2}+2 \cdot \frac{1}{2}=\frac{2-7 \sqrt{3}}{2}\)
Q తొలి నిరూపకాలు \(\left(\frac{-7-2 \sqrt{3}}{2}, \frac{2-7 \sqrt{3}}{2}\right)\)

iii) నూతన నిరూపకాలు (2, 0)
x’ = 2, y’ = 0
x = x’ cos θ – y’ sin θ
= 2. cos 60° – 0. sin 60°
= 2 . \(\frac{1}{2}\) – 0 . \(\frac{\sqrt{3}}{2}\) = 1 – 0 = 1
y = x’ sin θ + y’ cos θ
= 2. sin 60° + 0. cos 60°
= 2. \(\frac{\sqrt{3}}{2}\) + 0 . \(\frac{1}{2}\) = \(\sqrt{3}\)
Q తొలి నిరూపకాలు (1, \(\sqrt{3}\))

ప్రశ్న 9.
x² + 4xy + y² – 2x + 2y – 60 xy పదం లోపింపచేయడానికి అక్షాలను ఏ కోణంలో భ్రమణ పరివర్తన చేయాలో కనుక్కోండి. [June ’04]
సాధన:
x² + 4xy + y² – 2x + 2y – 6 = 0
ax² + 2hxy + by² + 2gx + 2fy + c = 0 తో
పోల్చగా a = 1, h = 2, b = 1, g = 1, f = 1, c = -6
నిరూపకాక్షాలకు ‘θ’ కోణం భ్రమణం చేస్తే

II.

ప్రశ్న 1.
అక్షాల సమాంతర పరివర్తన ద్వారా మూల బిందువును (2, 3) కు మార్చినప్పుడు, ఒక వక్రం రూపాంతరం చెందిన సమీకరణము x² + 3xy – 2y² + 17x – 7y – 11 = 0 అయితే వక్రం యొక్క మూల సమీకరణము కనుక్కోండి. [May ’11]
సాధన:
పరివర్తన సమీకరణాలు
x = x + h, y = y + k
x’ = x – h = x – 2, y’ = y – 3
పరివర్తిత సమీకరణము
x² + 3xy – 2y² + 17x – 7y – 11 = 0
తొలి సమీకరణము
(x – 2)² + 3(x – 2) (y – 3) – 2(y – 3)² + 17(x – 2) – 7(y – 3) – 11 = 0
x² – 4x + 4 + 3xy – 9x – 6y + 18 – 2y² + 12y – 18 + 17x – 34 – 7y + 21 − 11 = 0
x² + 3xy – 2y² + 4x – y – 20 = 0
ఇది కావలసిన మూల సమీకరణము

ప్రశ్న 2.
45°కోణంతో అక్షాలను భ్రమణం చేసినప్పుడు, రూపాంతరం చెందిన వక్రం సమీకరణము 17x² – 16xy + 17y = 225. వక్రం మూల సమీకరణాన్ని కనుక్కోండి. [T.S Mar. ’15; May ’12]
సాధన:
భ్రమణ కోణము = θ = 45
x’ = x cos θ + y sin θ = x cos 45 + y sin 45
= \(\frac{x+y}{\sqrt{2}}\)
y’ = -x sin θ + y cos θ = − -x sin 45 + y cos 45
= \(\frac{-x+y}{\sqrt{2}}\)
17x² – 16xy + 17y² = 225 యొక్క తొలి సమీకరణము

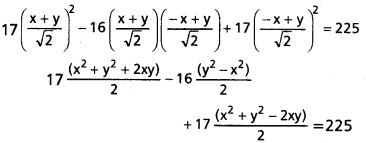
17x² + 17y² + 34xy – 16y² + 16x² + 17x² + 17y² – 34xy = 450
50x² + 18y² = 450
తొలి సమీకరణము
25x² + 9y² = 225

ప్రశ్న 3.
అక్షాలను a కోణంతో భ్రమణం చేసినప్పుడు, x cos α. + y sin α = p యొక్క రూపాంతర సమీకరణము కనుక్కోండి. [Mar. ’14, May ’07]
సాధన:
దత్త సమీకరణము x cos α + y sin α = p
∵ నిరూపకాక్షాలను కోణం భ్రమణం చేసాయి.
x = x’ cos α – y’ sin α
y = x’ sin α + y’ cos α
దత్త సమీకరణము పరివర్తిత రూపము
(x’ cos α – y’ sin α) cos α + (x’ sin a + y’ cos α) sin α = p
⇒ x’ (cos² α + sin² α) = p ⇒ x’ = p
దత్త సమీకరణము పరివర్తిత రూపం x = p

ప్రశ్న 4.
\(\frac{\pi}{6}\) కోణంతో అక్షాలను భ్రమణం చేసినప్పుడు, x² + 2\(\sqrt{3}\)xy – y² = 2a² యొక్క సమీకరణము కనుక్కోండి. [A.P Mar. ’15, ’12, ’07, ’04; May ’13, ’12]
సాధన:
θ = \(\frac{\pi}{6}\), x = X cos α + Y sin α
x = X cos \(\frac{\pi}{6}\) – Y sin \(\frac{\pi}{6}\)
= \(X \cdot \frac{\sqrt{3}}{2}-Y \cdot \frac{1}{2}=\frac{\sqrt{3} X-Y}{2}\)
y = X sin α + Y cos α = X. sin \(\frac{\pi}{6}\) + Y cos \(\frac{\pi}{6}\)
= \(X \cdot \frac{1}{2}+Y . \frac{\sqrt{3}}{2}=\frac{X+\sqrt{3} Y}{2}\)
రూపాంతర సమీకరణము

⇒ \(\frac{3 x^2-2 \sqrt{3} X Y+Y^2}{4}\) + \(\frac{2 \sqrt{3}\left[\sqrt{3} X^2-X Y+3 X Y-\sqrt{3} Y^2\right]}{4}\) – \(\frac{X^2+3 Y^2+2 \sqrt{3} X Y}{4}\) = 2a²
⇒ 3X² – 2\(\sqrt{3}\) XY + Y² + 2\(\sqrt{3}\) [\(\sqrt{3}\)X² + 2XY – \(\sqrt{3}\)Y²] – (x² + 3Y² + 2\(\sqrt{3}\)XY) = 8a²
⇒ 3x² – 2\(\sqrt{3}\)XY + Y² + 6X² + 4\(\sqrt{3}\)XY – 6Y² – X² – 3Y² – 2\(\sqrt{3}\) XY = 8a²
⇒ 8x² – 8y² = 8a² ⇒ X² – Y² = a²

ప్రశ్న 5.
\(\frac{\pi}{4}\) కోణంతో అక్షాలను భ్రమణం చేసినప్పుడు, 3x² + 10xy + 3y² = 9 యొక్క రూపాంతర
సమీకరణము కనుక్కోండి. [May ’11]
సాధన:
దత్త సమీకరణము
3x² + 10xy + 3y² – 9 = 0 ……………… (1)
భ్రమణ కోణము θ = \(\frac{\pi}{4}\)
(X, Y) లు (x, y) యొక్క నూతన నిరూపకాలు అనుకొనుము.
x = X cos θ – Y sin θ
= X cos \(\frac{\pi}{4}\) – y sin \(\frac{\pi}{4}\) = \(\frac{X-Y}{\sqrt{2}}\)
y = X sin θ + Y cos θ = X sin \(\frac{\pi}{4}\) + Y cos \(\frac{\pi}{4}\) = 2 \(\frac{X+Y}{\sqrt{2}}\)
(1) యొక్క రూపాంతర సమీకరణము
\(3\left(\frac{X-Y}{\sqrt{2}}\right)^2+10\left(\frac{X-Y}{\sqrt{2}}\right)\left(\frac{X+Y}{\sqrt{2}}\right)+3\left(\frac{X+Y}{\sqrt{2}}\right)^2-9=0\)
⇒ 3 \(\frac{\left(X^2-2 X Y+Y^2\right)}{2}\) + 10 \(\frac{\left(X^2-Y^2\right)}{2}\) + 3 \(\frac{\left(X^2+2 X Y+Y^2\right)}{2}\) – 9 = 0
⇒ 3x² – 6XY + 3y² + 10X² – 10Y² + 3X² + 6XY + 3Y² – 18 = 0
16X² – 4Y² – 18 = 0
∴ 8X² – 2Y² = 9
∴ 8X² – 2Y² = 9