AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Ex 3(b)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 3 సరళరేఖ Exercise 3(b) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Exercise 3(b)

అభ్యాసం – 3 (బి)

I.

ప్రశ్న 1.
రేఖ 4x – 3y = 12 కు నిరూపకాక్షాల మీద అంతరఖండాల వర్గాల మొత్తం కనుక్కోండి.
సాధన:
దత్త రేఖ సమీకరణము
\(\frac{4 x}{12}-\frac{3 y}{12}\) = 1
\(\frac{x}{3}+\frac{y}{-4}\) = 1
a = 3, b = – 4
వర్గాల మొత్తము = a² + b²
= 9 + 16 = 25

ప్రశ్న 2.
ఒక సరళరేఖ నిరూపకాక్షాల మధ్య గల భాగాన్ని (2p, 2q) సమద్విఖండన చేస్తే ఆ రేఖ సమీకరణం కనుక్కోండి.
సాధన:
అంతరఖండ రూపంలో AB సమీకరణము

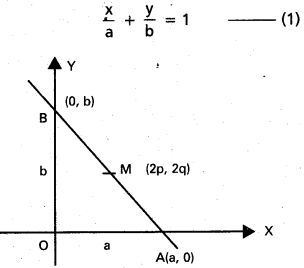
A నిరూపకాలు (a, 0), B నిరూపకాలు (0, b)
M మధ్య బిందువు AB
M నిరూపకాలు \(\left(\frac{a}{2}, \frac{b}{2}\right)\) = (2p, 2q)
\(\frac{a}{2}\) = 2p, \(\frac{b}{2}\) = 2q
(1) లో ప్రతిక్షేపిస్తే AB సమీకరణము
\(\frac{x}{4 p}+\frac{y}{4 q}\) = 1
\(\frac{x}{p}+\frac{y}{q}\) = 4

ప్రశ్న 3.
ax + by + c = 0 (abc ≠ 0), lx + my + n = 0 సమీకరణం ఒకే రేఖను సూచిస్తే, r = \(\frac{l}{a}=\frac{n}{c}\) అయినప్పుడు r విలువను m, b లలో కనుక్కోండి.
సాధన:
ax + by + c = 0,
lx + my + n = 0 లు ఒకే రేఖను సూచిస్తున్నాయి.
∴ \(\frac{l}{a}=\frac{m}{b}=\frac{n}{c}\) = r
\(\frac{m}{b}\) = r

ప్రశ్న 4.
రేఖ y = – \(\sqrt{3}\) x + 3, X – అక్షం ధన దిశలో అపసవ్య దిశలో చేసే కోణం కనుక్కోండి.
సాధన:
దత్త రేఖ సమీకరణము y = – \(\sqrt{3}\)x + 3
దత్తరేఖ X – అక్షం ధన దిశలో అపసవ్య దిశలో చేసిన కోణము α అనుకుందాం.
tan α = – \(\sqrt{3}\) = tan \(\frac{2\pi}{3}\)
α = \(\frac{2\pi}{3}\)

ప్రశ్న 5.
ఒక సరళరేఖ నిరూపకాక్షాల మీద చేసే అంతరఖండాలు a, ‘b అయితే మూల బిందువు నుంచి ఆ రేఖకు లంబ దూరమైన p విలువను a, b లలో కనుక్కోండి.
సాధన:
అంతరఖండ రూపంలో రేఖ సమీకరణము

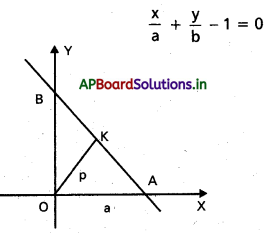
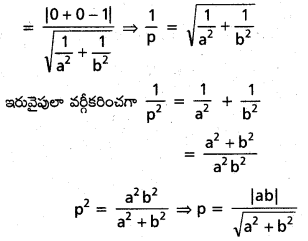
p = మూలబిందువు నుండి లంబంగా

II.

ప్రశ్న 1.
ఈ క్రింది వాటిలో మూల బిందువు నుంచి సరళరేఖ దూరాన్ని p సూచిస్తుంది. మూల బిందువు నుంచి సరళరేఖకు గీసిన ఒక అభిలంబ కిరణం X – అక్షం ధన దిశతో అపసవ్య దిశలో 0 కోణాన్ని చేస్తుంది. క్రింద ఇచ్చిన p, α విలువలు గల సరళరేఖల సమీకరణాలను కనుక్కోండి.
i) p = 5, α = 60°
ii) p = 6, α = 150°
iii) p = 1, α = \(\frac{7\pi}{4}\)
iv) p = 4, α = 90°
v) p = 0, α = 0
vi) p = 2\(\sqrt{2}\), α = \(\frac{5\pi}{4}\)
సాధన:
అభిలంబ రూపంలో రేఖ సమీకరణం
x cos α + y sin α = p
i) p = 5, α = 60°
cos α= cos 60° = \(\frac{1}{2}\)
sin α = sin 60° = \(\frac{\sqrt{3}}{2}\)
స్పర్శరేఖ సమీకరణము x . \(\frac{1}{2}\) + y . \(\frac{\sqrt{3}}{2}\) = 5
⇒ x + \(\sqrt{3}\) y = 10

ii) p = 6, α = 150°
cos α = cos 150° = cos (180° – 30°)
= -cos 30° = – \(\frac{\sqrt{3}}{2}\)
sin α = sin 150°
= sin (180° -30°)
= sin 30° = \(\frac{1}{2}\)
సరళరేఖ సమీకరణము
\(x \cdot\left(-\frac{\sqrt{3}}{2}\right)+y \cdot \frac{1}{2}\) = 6
– \(\sqrt{3}\) x + y = 12
లేదా \(\sqrt{3}\) x – y + 12 = 0

iii) p = 1, α = \(\frac{7\pi}{4}\)
cos α= cos 315° = cos (360° – 45°)
= cos 45° = \(\frac{1}{\sqrt{2}}\)
sin α = sin 315° = sin (360° – 45°)
= – sin 45° = –\(\frac{1}{\sqrt{2}}\)
సరళరేఖ సమీకరణము
x . \(\frac{1}{\sqrt{2}}\) – y . \(\frac{1}{\sqrt{2}}\) = 1
x – y = \(\sqrt{2}\)
x – y – \(\sqrt{2}\) = 0

iv) p = 4, α = 90°
cos α = cos 90° = 0, sin α = sin 90° = 1
సరళరేఖ సమీకరణము x. 0 + y . 1 = 4
y = 4

v) p = 0, α = 0
cos α = cos 0 = 1, sin α = sin 0 = 0
సరళరేఖ సమీకరణము x. 1 + y . 0 = 0
x = 0

vi) p = 2\(\sqrt{2}\), α = \(\frac{5\pi}{4}\)
cos α = cos 225° = cos (180° + 45°)
= -cos 45° = –\(\frac{1}{\sqrt{2}}\)
sin α = sin 225° = sin (180° + 45°)
= -sin 45° = – \(\frac{1}{\sqrt{2}}\)
సరళరేఖ సమీకరణము
\(x\left(-\frac{1}{\sqrt{2}}\right)+y\left(-\frac{1}{\sqrt{2}}\right)=2 \sqrt{2}\)
-x – y = 4
లేదా x + y + 4 = 0

ప్రశ్న 2.
కింది సమస్యలలో ఇచ్చిన వాలుతో, ఇచ్చిన బిందువు గుండా పోయే సరళరేఖల సమీకరణాలు సౌష్ఠవ రూపంలో కనుక్కోండి.
i) \(\sqrt{3}\) (2, 3)
ii) –\(\frac{1}{\sqrt{3}}\), (-2, 0)
iii) -1, (1, 1)
సాధన:
i) సౌష్ఠవ రూపంలో సరళరేఖ సమీకరణము
\(\frac{x-x_1}{\cos \alpha}=\frac{y-y_1}{\sin \alpha}\) = r
(x₁, y₁) = (2, \(\sqrt{3}\))
m = tan α = \(\sqrt{3}\) ⇒ α = 60°
cos α = cos 60° = \(\frac{1}{2}\)
sin α = sin 60° = \(\frac{\sqrt{3}}{2}\)
సౌష్టవ రూపంలో సరళరేఖ సమీకరణము
\(\frac{x-2}{\cos \frac{\pi}{3}}=\frac{y-3}{\sin \frac{\pi}{3}}\)

ii) (x, y) = (-2, 0)
tan α = – \(\frac{1}{\sqrt{3}}\) ⇒ α = 180° – 30° = 150°
సరళరేఖ సమీకరణము
\(\frac{x+2}{\cos 150^{\circ}}=\frac{y}{\sin 150^{\circ}}\)

iii) tan α = -1, α = 180° – 45° = 135°
(x₁, y₁) = (1, 1)
సరళరేఖ సమీకరణము
\(\frac{x-1}{\cos \left(\frac{3 \pi}{4}\right)}=\frac{y-1}{\sin \left(\frac{3 \pi}{4}\right)}\)

ప్రశ్న 3.
క్రింది సమీకరణాలను
a) వాలు – అంతరఖండ రూపం
b) అంతరఖండ రూపం
c) అభిలంబ రూపంలోకి మార్చండి.
i) 3x + 4y = 5
ii) 4x – 3y + 12 = 0
iii) \(\sqrt{3}\) x + y = 4
iv) x + y + 2 = 0
v) x + y – 2 = 0
vi) \(\sqrt{3}\) x + y + 10 = 0
సాధన:
i) 3x + 4y = 5
వాలు – అంతరఖండ రూపము:
4y = -3x + 5
y = \(\left(-\frac{3}{4}\right) x+\left(\frac{5}{4}\right)\)
అంతరఖండ రూపము :
3x + 4y = 5
\(\frac{3 x}{5}+\frac{4 y}{5}\) = 1
\(\frac{x}{\left(\frac{5}{3}\right)}+\frac{y}{\left(\frac{5}{4}\right)}\) = 1
అభిలంబ రూపము :
3x + 4y = 5
\(\sqrt{9+16}\) = 5 తో భాగించగా
\(\frac{3}{5}\) x + \(\frac{4}{5}\) y = 1
cos α = \(\frac{3}{5}\), sin α = \(\frac{4}{5}\) ⇒ tan α = \(\frac{4}{3}\)
x cos α + y sin α = 1

ii) 4x – 3y + 12 = 0
వాలు – అంతరఖండ రూపము:
3y = 4x + 12
y = \(\left(\frac{4}{3}\right)\) x + 4
అంతరఖండ రూపము :
4x – 3y + 12 = 0
-4x + 3y = 12
\(\frac{-4 x}{12}+\frac{3 y}{12}\) = 1
\(\frac{x}{(-3)}+\frac{y}{4}\) = 1
అభిలంబ రూపము :
4x – 3y + 12 = 0
-4x + 3y = 12
\(\sqrt{16+9}\) = 5 తో భాగించగా
\(\left(\frac{-4}{5}\right) x+\left(\frac{3}{5}\right) y=\frac{12}{5}\)
cos α = –\(\frac{4}{5}\), sin α = \(\frac{3}{5}\) ⇒ tan α = –\(\frac{3}{4}\)
x cos α + y sin α = \(\frac{12}{5}\)

iii) \(\sqrt{3}\) x + y = 4
వాలు – అంతరఖండ రూపము :
\(\sqrt{3}\) x + y = 4
y = –\(\sqrt{3}\) x + 4
అంతరఖండ రూపము :

iv) x + y + 2 = 0 [Mar. ’12]
వాలు – అంతరఖండ రూపము :
x + y + 2 = 0
y = -x – 2
= (-1)x + (-2)
అంతరఖండ రూపము:
x + y + 2 = 0
-x – y = 2
\(\frac{x}{(-2)}+\frac{y}{(-2)}\) = 1
అభిలంబ రూపము :
x + y + 2 = 0
-x – y = 2
\(\sqrt{1+1}=\sqrt{2}\) తో భాగించగా
\(\left(-\frac{1}{\sqrt{2}}\right) x+\left(-\frac{1}{\sqrt{2}}\right) y=\sqrt{2}\)
\(x \cos \left(\frac{5 \pi}{4}\right)+y \sin \left(\frac{5 \pi}{4}\right)=\sqrt{2}\)

v) x + y – 2 = 0
వాలు – అంతరఖండ రూపము :
x + y – 2 = 0
y = -x + 2
అంతరఖండ రూపము:
x + y – 2 = 0
x + y = 2
\(\frac{x}{2}+\frac{y}{2}\) = 1
అభిలంబ రూపము :
x + y – 2 = 0
x + y = 2
\(\sqrt{1+1}=\sqrt{2}\) తో భాగించగా
\(\frac{1}{\sqrt{2}}\) . x + \(\frac{1}{\sqrt{2}}\) . y = \(\sqrt{2}\)
x cos \(\left(\frac{\pi}{4}\right)\) + y sin \(\left(\frac{\pi}{4}\right)\) = \(\sqrt{2}\)

vi) \(\sqrt{3}\) x + y + 10 = 0
వాలు – అంతరఖండ రూపము:
\(\sqrt{3}\) x + y + 10 = 0
y = –\(\sqrt{3}\) x – 10
అంతరఖండ రూపము :

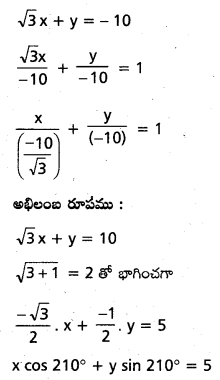
ప్రశ్న 4.
సరళరేఖ x tan α + y sec α = 1 (0 ≤ α ≤ \(\frac{\pi}{2}\)) నిరూపకాక్షాల మీద చేసే అంతర ఖండాల లబ్దము sin α అయితే C. కనుక్కోండి.
సాధన:
సరళరేఖ సమీకరణము x tan α + y sec α = 1
\(\frac{x}{\cot \alpha}+\frac{y}{\cos \alpha}\) = 1
a = cot α, b = cos α
ab = sin α అని ఇవ్వబడింది.
cot α . cos α = sin α
\(\frac{\cos ^2 \alpha}{\sin \alpha}\) = sin α ⇒ cos² α = sin² α
tan² α = 1 = tan α = +1
α = 45°

ప్రశ్న 5.
ఒక చల (variable) సరళరేఖ నిరూపకాక్షాలతో చేసే అంతరఖండాల విలోమాల మొత్తం స్థిరం అయితే ఆ రేఖ ఒక స్థిర బిందువు గుండా పోతుందని చూపండి.
సాధన:
అంతరఖండ రూపంలో రేఖ సమీకరణము

ప్రశ్న 6.
సరళరేఖ నిరూపకాక్షాలతో చేసే అంతరఖండాలు a, b. మూల బిందువును స్థిరంగా ఉంచి అక్షాలకు ఒక దత్త కోణం గుండా తిప్పినప్పుడు ఆ రేఖ L నూతన అక్షాలతో చేసే అంతరఖండాలు p, q అయితే \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{p^2}+\frac{1}{q^2}\) అని చూపండి.
సాధన:
అంతరఖండ రూపంలో తొలి వ్యవస్థలో సరళరేఖ సమీకరణము
\(\frac{x}{a}+\frac{y}{b}\) = 1
⇒ \(\frac{x}{a}+\frac{y}{b}\) – 1 = 0
మూల బిందువు నుండి లంబదూరము
= \(\frac{|0+0-1|}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}\) …………… (1)
రెండవ వ్యవస్థలో అంతరఖండ రూపంలో సరళరేఖ సమీకరణము
\(\frac{x}{p}+\frac{y}{q}\) = 1
⇒ \(\frac{x}{p}+\frac{y}{q}\) – 1 = 0
మూల బిందువు నుండి లంబ దూరము
= \(\frac{|0+0-1|}{\sqrt{\frac{1}{p^2}+\frac{1}{q^2}}}\) ……………… (2)

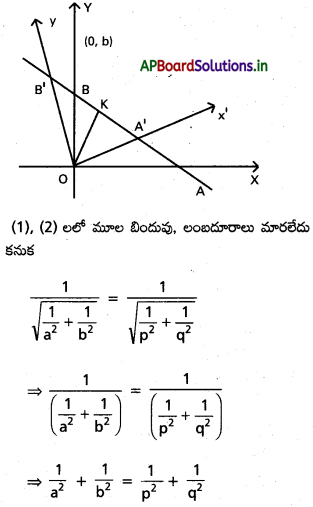
ప్రశ్న 7.
\(\frac{x}{a}+\frac{y}{b}\) = 1 సమీకరణాన్ని a > 0, b > 0 అయినప్పుడు అభిలంబ రూపంలోకి రూపాంతరం చేయండి. ఆ రేఖకు మూల బిందువు నుండి లంబదూరం p అయితే \(\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}\) అని చూపండి.
సాధన:
సరళరేఖ సమీకరణము
\(\frac{x}{a}+\frac{y}{b}\) = 1
bx + ay = ab
\(\sqrt{a^2+b^2}\) తో భాగించగా

III.

ప్రశ్న 1.
ఒక సరళరేఖ A(-2, 1) నుంచి పోతూ X – అక్షం ధన దిశలో 30° కోణం చేస్తుంది. ఆ సరళరేఖపై A నుంచి 4 యూనిట్ల దూరంలో ఉన్న బిందువులను కనుక్కోండి.
సాధన:
దత్త రేఖ మీది ఏదేని బిందువు నిరూపకాలు
(x₁ + r cos α, y₁ + r sin α)
α = 30° ⇒ cos α = cos 30° = \(\frac{\sqrt{3}}{2}\)
sin α = sin 30° = \(\frac{1}{2}\)
(x₁, y₁) = (-2, 1) ⇒ x₁ = -2, y₁ = 1
r = 4 గా తీసుకుంటే P నిరూపకాలు
(-2 + 4 . \(\frac{\sqrt{3}}{2}\), 1 + 4 . \(\frac{1}{2}\)) = (-2 + 2\(\sqrt{3}\), 3)
r = – 4 గా తీసుకుంటే P నిరూపకాలు
(-2 – 4 . \(\frac{\sqrt{3}}{2}\), 1 – 4 . \(\frac{1}{2}\)) = (-2 – 2\(\sqrt{3}\), -1)

ప్రశ్న 2.
3x – 4y – 1 = 0 రేఖపై ఉంటూ, బిందువు (3, 2) నుంచి 5 యూనిట్లు దూరంలో ఉన్న బిందువులను కనుక్కోండి. [A.P Mar. ’15]
సాధన:
సౌష్ఠవ రూపంలో సరళరేఖ సమీకరణము
\(\frac{x-3}{\cos \alpha}=\frac{y-2}{\sin \alpha}\) = r
P నిరూపకాలు
(3 + r cos α, 2 + r sin α) = (3 + 5 cos α, 2 + 5 sin α)
P బిందువు 3x – 4y – 1 – 0 రేఖపై ఉంది.
3(3+ 5 cos α) – 4(2 + 5 sin α) − 1 = 0
9 + 15 cos α – 8 – 20 sin α – 1 = 0
15 cos α – 20 sin α = 0
15 cos α = + 20 sin α
tan α = + \(\frac{3}{4}\)
సందర్భం i) : cos α = +\(\frac{4}{5}\), sin α = \(\frac{3}{5}\)
సందర్భం ii) : cos α = –\(\frac{4}{5}\), sin α = –\(\frac{3}{5}\)

సందర్భం i) : P నిరూపకాలు
(3 + 5 . \(\frac{4}{5}\), 2 + 5 . \(\frac{3}{5}\)) = 17, 5)
సందర్భం ii): P నిరూపకాలు
(3 – 5 . \(\frac{4}{5}\), 2 – 5 . \(\frac{3}{5}\)) = (-1, -1)

ప్రశ్న 3.
X- అక్షం ధన దిశలో అపసవ్య దిశలో 7/3 కోణం చేసే ఒక సరళరేఖ Y- అక్షం మీద ధన అంతరఖండం చేస్తోంది. ఆ సరళరేఖ మూలబిందువు నుంచి 4 దూరంలో ఉంటే, ఆ రేఖ సమీకరణాన్ని కనుక్కోండి.
సాధన:
α = 7/3, p = 4 అని ఇవ్వబడింది.
m = tan α = tan 60° = \(\sqrt{5}\)
వాలు – అంతరఖండ రూపంలో సరళరేఖ సమీకరణము
y = \(\sqrt{3}\) x + c
\(\sqrt{3}\) x – y + c = 0
మూల బిందువు నుండి పోయే ధృవము = 4
\(\frac{|0-0+c|}{\sqrt{3+1}}\) = 4
|c| = 4 × 2 = 8
c = +8
c > 0
∴ c = 8
సరళరేఖ సమీకరణము \(\sqrt{3}\) x – y + 8 = 0

ప్రశ్న 4.
A (2, 1) బిందువు గుండాపోయేటట్లు గీసిన ఒక సరళరేఖ x + y = 9 రేఖను ఖండించే బిందువు A నుంచి 3\(\sqrt{2}\) దూరంలో ఉంటే, ఆ రేఖ సమీకరణాన్ని కనుక్కోండి.
సాధన:
L – రేఖ X – అక్షం ధన దిశలో α కోణం చేస్తుందను కుందాము.
ఈ రేఖమీది ఏదేని బిందువు నిరూపకాలు
= (x₁ + r cos α₁, y₁ + r sin α)
= (2 + 3\(\sqrt{2}\) cos α 1 + 3\(\sqrt{2}\) sin α)
ఈ బిందువు x + y = 9 రేఖ మీద ఉంది.
2 + 3\(\sqrt{2}\) cos α + 1 + 3\(\sqrt{2}\) sin α = 9
3\(\sqrt{2}\) (cos α + sin α) = 6
cos α + sin α = \(\frac{6}{3 \sqrt{2}}\) = \(\sqrt{2}\).
\(\frac{1}{\sqrt{2}}\) . cos α + \(\frac{1}{\sqrt{2}}\) sin α = 1
cos α . cos 45° + sin α . sin 45° = 1
cos (α – 45°) = cos 0°
α – 45° = 0 ⇒ α = 45° = \(\frac{\pi}{4}\)

ప్రశ్న 5.
రుణ వాలుగల ఒక సరళరేఖ L, బిందువు, (8, 2) గుండా పోతూ, ధన నిరూపకాక్షాలను P, Q ల వద్ద ఖండిస్తోంది. O మూల బిందువు, ఓ చలిస్తూ ఉంటే OP + OQ కు కనిష్ఠ విలువ కనుక్కోండి.
సాధన:
సరళరేఖ వాలు – m అనుకొనుము.
సరళరేఖ సమీకరణం y – 2 = -m (x – 8)
mx + y – (2 + 8m) = 0
mx + y = 2 + 8m


∴ కనిష్ఠ విలువ = 18