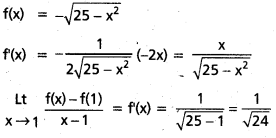AP Inter 1st Year Maths 1B Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Ex 8(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Exercise 8(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Exercise 8(a)

అభ్యాసం – 8 (ఎ)

I. క్రింది అవధులను గణించండి.

ప్రశ్న 1.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow a
\end{gathered}\frac{x^2-a^2}{x-a}\)
సాధన:

ప్రశ్న 2.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 1
\end{gathered}\) (x² + 2x + 3)
సాధన:
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 1
\end{gathered}\) (x² + 2x + 3) = 1² + 2 . 1 + 3
= 1 + 2 + 3 = 6

ప్రశ్న 3.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\frac{1}{x^2-3 x+2}\)
సాధన:
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\frac{1}{x^2-3 x+2}\)
= \(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\frac{1}{0-0+2}\) = \(\frac{1}{2}\)

ప్రశ్న 4.
\(\begin{gathered}
\text { Lt } \\
\mathrm{x} \rightarrow \mathrm{3}
\end{gathered}\frac{1}{x+1}\)
సాధన.
\(\begin{gathered}
\text { Lt } \\
\mathrm{x} \rightarrow \mathrm{3}
\end{gathered}\frac{1}{x+1}\)
= \(\frac{1}{3+1}\)
= \(\frac{1}{4}\)

ప్రశ్న 5.
\(\begin{gathered}
\text { Lt } \\
\mathrm{x} \rightarrow \mathrm{1}
\end{gathered}\frac{2 x+1}{3 x^2-4 x+5}\)
సాధన:
\(\begin{gathered}
\text { Lt } \\
\mathrm{x} \rightarrow \mathrm{1}
\end{gathered}\frac{2 x+1}{3 x^2-4 x+5}\)
= \(\frac{2.1+1}{3.1^2-4.1+5}\)
= \(\frac{3}{4}\)

ప్రశ్న 6.
\(\begin{gathered}
\text { Lt } \\
\mathrm{x} \rightarrow \mathrm{1}
\end{gathered}\frac{x^2+2}{x^2-2}\)
సాధన:

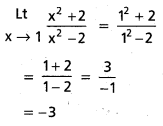
ప్రశ్న 7.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 2
\end{gathered}\left(\frac{2}{x+1}-\frac{3}{x}\right)\)
సాధన:

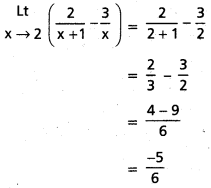
ప్రశ్న 8.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\left[\frac{x-1}{x^2+4}\right]\)
సాధన:
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\left[\frac{x-1}{x^2+4}\right]\)
= \(\frac{0-1}{0+4}\) = –\(\frac{1}{4}\)

ప్రశ్న 9.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\) x^3/2 (x > 0)
సాధన:
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\) x^3/2 (x > 0) = 0^3/2 = 0

ప్రశ్న 10.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\) (\(\sqrt{x}\) + x^5/2) (x > 0)
సాధన:
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\) (\(\sqrt{x}\) + x^5/2)
= \(\sqrt{0}\) + 0^5/2 = 0 + 0 = 0

ప్రశ్న 11.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\) x² cos \(\frac{2}{x}\)
సాధన:
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\) x² . \(\begin{gathered}
\text { Lt } \\
x \rightarrow 0
\end{gathered}\) cos \(\frac{2}{x}\) = 0 . k
|k| ≤ 1 = 0

ప్రశ్న 12.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 3
\end{gathered}\frac{x^2-9}{x^3-6 x^2+9 x+1}\)
సాధన:
\(\frac{9-9}{27-6(9)+27+1}=\frac{0}{54-54+1}=\frac{0}{1}\)
= 0

ప్రశ్న 13.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 1
\end{gathered}\left[\frac{x-1}{x^2-x}-\frac{1}{x^3-3 x^2+2 x}\right]\)
సాధన:

ప్రశ్న 14.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 3
\end{gathered}\frac{x^4-81}{2 x^2-5 x-3}\)
సాధన:

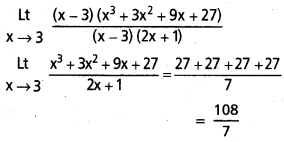
ప్రశ్న 15.
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 3
\end{gathered}\frac{x^2-8 x+15}{x^2-9}\)
సాధన:

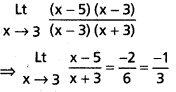
ప్రశ్న 16.
f(x) = –\(\sqrt{25-x^2}\) అయితే
\(\begin{gathered}
\text { Lt } \\
x \rightarrow 1
\end{gathered}\frac{f(x)-f(1)}{x-1}\) ను కనుక్కోండి.
సాధన: